基于PHD的粒子滤波检测前跟踪改进算法

(1.海军航空大学， 山东烟台 264001;2.中国民航科学技术研究院机场研究所， 北京 100028)

0 引言

现代战场环境下随着以无人机为代表的航空器的广泛应用，其雷达散射截面积较小，回波信号功率、信噪比会大大降低，从而导致雷达的检测性能急剧下降[1-2]。检测前跟踪(TBD)方法利用多帧原始观测数据联合实现检测和跟踪过程，与传统检测方法相比，针对低信噪比目标的检测性能更加优异，受到越来越多的关注[3]。典型的TBD方法包括Hough变换[4]、动态规划[5]、粒子滤波[6]等实现形式。由于当今多目标跟踪[7]问题中，应用随机集理论(RFS)能够避免数据关联操作，将随机集理论迁移到TBD领域也已成为了一大研究趋势。

为减少RFS理论中多目标最优贝叶斯递推的算法复杂度，Mahler[8]率先提出次最优的概率假设密度(PHD)滤波算法。该滤波迭代多目标后验概率密度的一阶矩，完成多目标的数目估计；其次根据目标估计数，在概率假设密度函数的峰值点处提取目标状态[9]。作为RFS理论框架下的典型滤波器，PHD滤波器自始至终迭代传递多目标整体的后验概率密度，因此在跟踪多个数量变化的目标同时，能有效地规避复杂的数据关联与配对，在保证算法实时性的同时，有效地提高跟踪精度[10]。将PHD滤波器应用至TBD中，可以更好地解决多目标TBD问题，但该方面研究仍处于起步阶段，性能还需不断完善，为此不少文献[11-12]提出了诸多改进方法。

本文针对现有基于PHD的粒子滤波检测前跟踪的位置估计精度较低的缺陷进行改进，受文献[13]的启发，结合当前量测值，在滤波的预测和更新步骤之间加入多目标粒子群优化，使粒子经过量测驱动向后验概率密度较大方向移动；然后在目标状态提取阶段，使用基于密度的DBSCAN数据聚类方法，将经由粒子群优化算法改良分布形态的粒子进行聚类提取目标的估计状态。经过仿真实验表明，改进后的算法相比原有的PHD-TBD在多目标位置估计上性能改善明显。

1 系统运动模型和观测模型

1.1 目标运动模型

目标运动模型设计为CV运动模型。多目标群体xk,1,…,xk,Num中第t个目标的运动方程为

xk,t=Fkxk-1,t+wk

(1)

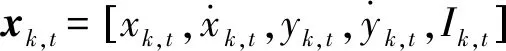
1.2 雷达系统观测模型

借鉴文献[14]在关于多普勒雷达的观测模型，雷达观测范围内共有Ur个距离分辨单元，Ud个多普勒单元和Ub个方位单元。在雷达观测的Ur×Ud×Ub个单元中，得到的功率观测值为

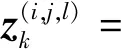
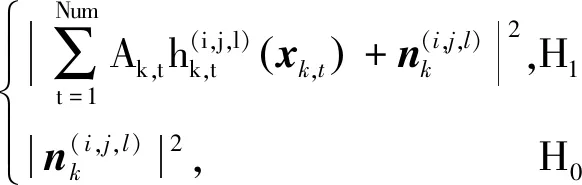
(2)

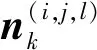
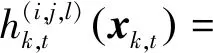
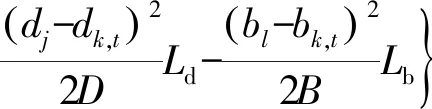
(3)

式中:R，D和B表示与距离、多普勒和方位单元尺寸分辨率，分别根据带宽、积累时间和波束宽度决定；Lr，Ld和Lb分别表示3个观测维度上的损耗系数；rk,t，dk,t和bk,t表示k时刻目标t所处的距离、多普勒和方位单元;ri，dj和bl表示(i,j,l)单元的距离、多普勒和方位信息。

依据量测模型，目标似然函数可表示为

p(zk|xk,1,xk,2,…,xk,Num)=

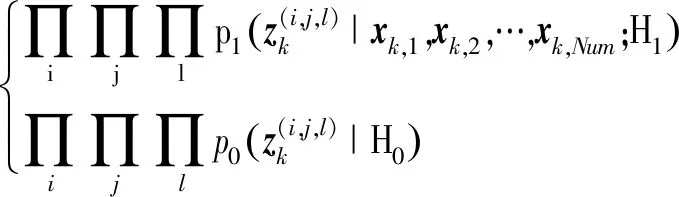
(4)

式中，p0表示没有目标时(i,j,l)单元处噪声的似然函数，p1表示存在Num个目标时(i,j,l)单元目标加噪声的似然函数。

(5)

(6)

由此得到似然比函数Lk的计算如下：

(7)

2 改进的雷达PSO-PHD-TBD算法

改进之后的PSO-PHD-TBD算法主要借助于多目标粒子群优化算法以及基于密度聚类的DBSCAN算法相结合提高对目标的位置估计精度。2.1节着重描述多目标粒子群优化算法，2.2节强调对粒子进行基于密度聚类，2.3节展示PSO-PHD-TBD的具体实施步骤，并在3.2节3)中给出了具体的算法复杂度的分析。

2.1 粒子群优化算法

粒子群优化算法(Particle Swarm Optimization, PSO)通过粒子个体通过适应度目标函数的函数值信息进行粒子优选，完成对最优条件的搜索[15]。算法中每个粒子i具有位置和搜索速度，代表最优结果的可能取值。算法首先定义适应度目标函数，通过迭代寻找最优解。迭代操作按照式(8)、式(9)更新每个粒子的运动信息，使得每个粒子移动，经过对粒子的个体最优解pi筛选，在搜索全局极值gi的同时实现对集群分布的优化[16]。

vi=wvi+c1R1·(pi-xi)+c2R2·(gi-xi)

(8)

xi+1=xi+rvi

(9)

式中，R1和R2在区间(0,1)内随机取值，w为惯性系数，c1和c2为正实数，代表粒子向个体最优解和全局最优解移动的权重，xi和xi+1为粒子状态，vi为搜索速度，r为更新因子。

在多目标的检测前跟踪过程中，由于存在多个适应度目标函数之间相互冲突，一个目标函数的最优解往往并不能满足剩余目标函数最优解，因此每一个目标的最优解只能陷入局部最优解。而多目标粒子群优化(Multi-Object PSO, MOPSO)方法，借助NSGA-Ⅱ算法实现利用多个适应度目标函数筛选粒子，能够将粒子引导、移动以求取多目标Pareto最优解集[17-18]。作为遗传算法上的改进[19]，算法关键步骤在以下3个过程：

1) 精英选择策略。为了避免盲目的更新迭代而采用的一种方法，将更新前后的粒子集群同时存储进行优先选择。

2) 快速非支配排序。将粒子群中所有粒子的解进行比较，得出粒子目标函数值之间的支配关系，对种群分层，从而指引搜索向Pareto最优解集方向进行。

3) 计算拥挤距离。计算粒子的拥挤距离是为了能够将处于相同非支配层的粒子进行选择性排序。对同一非支配层L中所有n个粒子的拥挤距离disi初始化。

disi=0,i=1,2,…,n

(10)

对同层的个体按照第m个目标函数值升序排列：对于排序边缘上的粒子，令dis0=disn=D(D为一较大乘数)；对排序中间的粒子i，求取拥挤距离disi。

disi=∑mWmdisi,m

(11)

disi,m=disi,m+(disi+1,m-disi-1,m)/(fmax,m-fmin,m)

(12)

式中disi+1,m，disi-1,m为粒子i的相邻粒子对第m个目标函数的函数值，fmax,m，fmin,m分别为层中粒子对第m个目标函数的最大值和最小值。基于所有的适应度目标函数，都需要循环上述步骤，每一个目标函数拥有与之相对应的函数权重Wm，对所有的Wmdisi,m求和得到粒子i的拥挤距离disi。

为了避免陷入局部最优解的问题，再加入变异机制增加粒子的多样性。粒子分为三部分，一为选择不变异，二为统一增加变异量，三为随机添加变异量。

2.2 基于密度的数据聚类方法

粒子群优化方法使粒子都向后验概率密度较大的区域进行移动，这样使得基于密度进行聚类的方法得到应用。基于密度的聚类算法其实是基于距离的聚类的类型(这一点和通常使用的K-means聚类方法类似)。只要邻近区域的粒子密度超出了阈值Thmin，就可以继续对粒子聚类。DBSCAN是其中具有代表性的一种，该方法根据密度阈值Thmin控制聚类的增长，其主要目的是通过过滤低密度区域来发现稠密样本点聚类。

DBSCAN方法将聚类定义为高密度相连点的最大集合，并能发现任意形状的聚类[20]。为了实现粒子聚类，算法描述需要输入一个如数目为N的粒子群，一个最小半径E，密度阈值Thmin。对于尚未被聚类的粒子，算法主要统计该粒子周围半径E范围内的粒子数量，如果小于Thmin，则该点为噪声点；如果抽出的粒子其最小半径E范围内的粒子数目超出阈值Thmin，则该点成为一个新聚类的核心点，将所有从该点密度可达的点加入到当前聚类中，如果该点密度可达节点中有已经生成聚类的核心点，则将两个聚类合并形成一个聚类，新聚类的核心点为原来合并的核心点的集合。

2.3 PSO-PHD-TBD算法实施步骤

借助于粒子滤波(也称为序贯蒙特卡洛[21])的实现形式，PSO-PHD-TBD的具体实施步骤如下：

1) 初始化

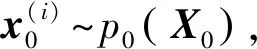
(13)

2) 预测

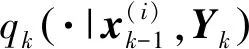
(14)

并根据下式计算存活粒子的权重：

(15)

假设k时刻新生目标的采样粒子数为Jk，则根据建议密度pk(·|Yk)采样新生目标的粒子：

(16)

并根据式(17)计算新生粒子的权重：

(17)

式中,γk为新生粒子的概率假设密度函数。

3) PSO优化

在粒子的预测之后，将最新的观测值引入优化采样过程，根据获得的观测定义优化所需的适应度目标函数：

(18)

(19)

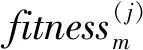
为了避免预测概率密度与似然函数的重叠区域较小的问题，在此时设置粒子群优化算法，结合量测信息，由量测驱动粒子集通过式(8)、式(9)不断更新迭代向高似然比区域移动，提高每一个粒子的利用效率，使粒子不断地向高似然状态靠近[13]。具体的实施步骤如下：

①经过对父代种群粒子进行式(8)、式(9)的运算更新得到子代种群，对子代种群中的粒子进行变异操作，同时父代粒子的权重也传递给子代对应的粒子；

②将两个种群合并，进行非支配排序，计算整个粒子集之间的拥挤距离；

③选择生成新的父代种群粒子，对粒子权重重新进行归一化处理，继续进行下一轮的优化迭代，直到适应度函数值达到阈值Thpso。

4) 更新

对于k时刻已经过优化处理的所有粒子i=1,2,…,Lk-1+Jk，根据式(20)更新其权重：

(20)

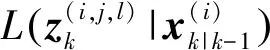
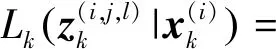
(21)

(22)

(23)

σ2为观测噪声协方差，而权重表达式分母的另一项，

(24)

式中，

(25)

5) 数目估计、重采样以及状态提取

根据粒子权重之和估计目标数目

(26)

3 算法仿真

3.1 仿真条件设置

本节将给出多目标TBD的应用实例，仿真中假定目标运动满足匀速模型。扫描周期T=1 s，目标运动近似为线性运动，运动方程同式(1)。假设雷达的测量区域设置为[0,2 000 m]×[0,2 000 m]，雷达位于原点位置，距离单元分辨率R=20 m，多普勒单元分辨率D=1 m/s，方位单元分辨率B=1°。为便于算法性能对比，一共产生40帧仿真数据(文中将一次扫描数据设置为一帧数据，由于扫描周期为1 s，数据信息一共历时40 s)，经过100次蒙特卡洛实验取均值。

仿真设置在3种不同信噪比条件下(分别为9，7和5 dB)，雷达的观测区域存在6个目标，目标初始运动状态如表1所示。假定目标的RCS没有起伏，满足Swerling 0型假设；目标存活概率PS=0.98，新生概率Pb=0.02；过程噪声协方差为0.001；目标强度噪声协方差为0.01；粒子数L=500；SNR=10lg(P/2σ2)，观测噪声协方差为1，则可依据信噪比以及观测噪声协方差σ2来得到目标功率。目标强度设定I=20，粒子的强度服从介于[15,25]之间的均匀分布。

表1 目标初始运动状态

每个目标分别设置1 000个粒子，设置高斯混合模型从中采样得出500个新生粒子，高斯混合模型一共包含3种高斯分布x(i)～N(x;m(i),P),i=1,2,3相组合，具体参数分别为m(1)=[250 m,0 m/s,1 500 m,0 m/s,I]，m(2)=[1 000 m,0 m/s,1 000 m,0 m/s,I]，m(3)=[1 500 m,0 m/s,250 m,0 m/s,I]，P=diag([20 m 20 m/s 20 m 20 m/s 1])2，3种目标的权重一致。多目标粒子群优化过程中，在一个时刻k内迭代次数gen=10，目标函数阈值Thpso=0.7，达到迭代次数后以适应度函数阈值为优化结束的最终条件。DBSCAN聚类时设置参数最小半径E=5 m和密度阈值Thmin=10。

整个仿真场景不考虑新目标衍生。目标真实运动状态如图1所示，图中三角形表示目标起始位置，正方形表示消失位置。

图1 目标的真实航迹

图2表示9 dB信噪比条件下，监视区域在第25帧时已转换为笛卡尔坐标系的回波能量信息，6个目标都悉数出现在观测区域，完全淹没在噪声之中。

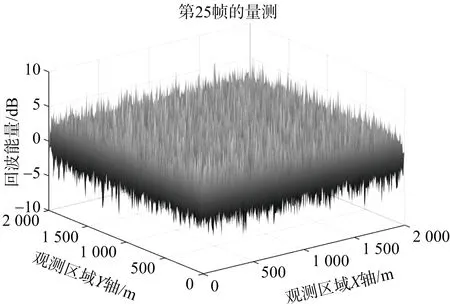
图2 第25帧的观测信息

3.2 仿真结果分析

本文将所提出的PSO-PHD-TBD算法和常规PHD-TBD算法对同一仿真场景在信噪比进行性能分析。

1) 对目标的数目估计情况

经过100次蒙特卡洛的仿真实验，得到平均每个时刻的估计数目如图3所示。

两种算法在随着信噪比的降低，两算法的估计性能都出现了相应的下降。相较之下，PSO-PHD-TBD的性能更加稳定。图4列举出不同信噪比条件下基于100次蒙特卡洛仿真计算而来的数目估计标准差，表2展示了40帧数据目标数目估计标准差的均值，统计值越小代表目标数目估计越准确。根据图4和表2可以看出在数目估计精度上PSO-PHD-TBD算法相比于PHD-TBD算法也有较为明显的提高。

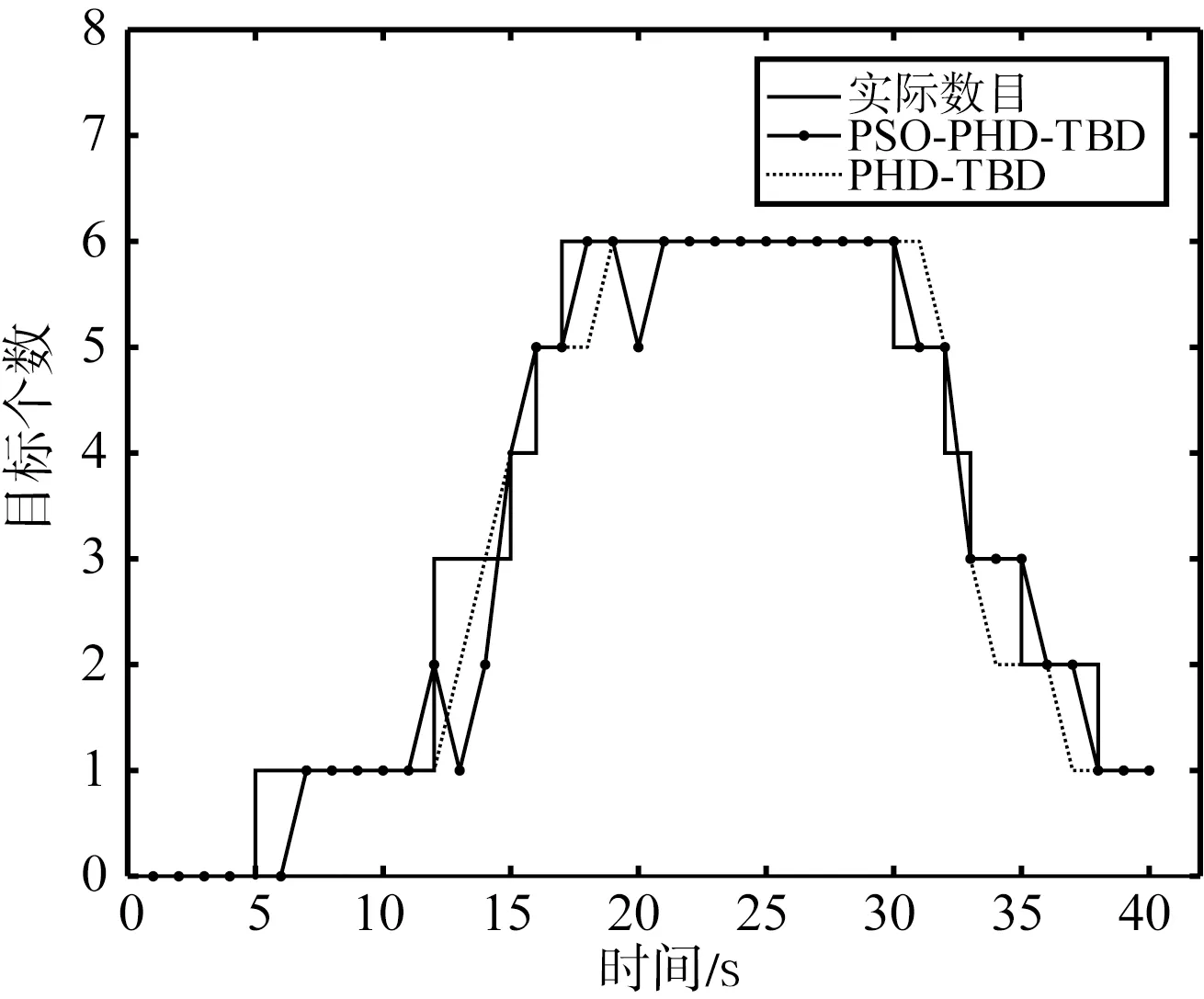
(a) 9 dB的数目估计

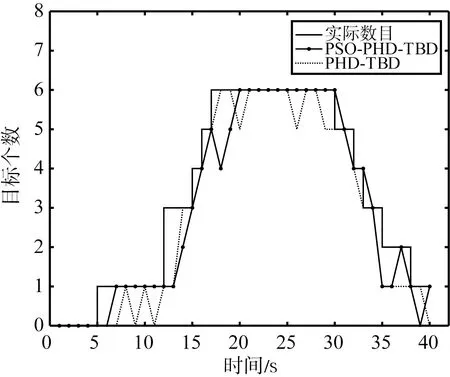
(b) 7 dB的数目估计

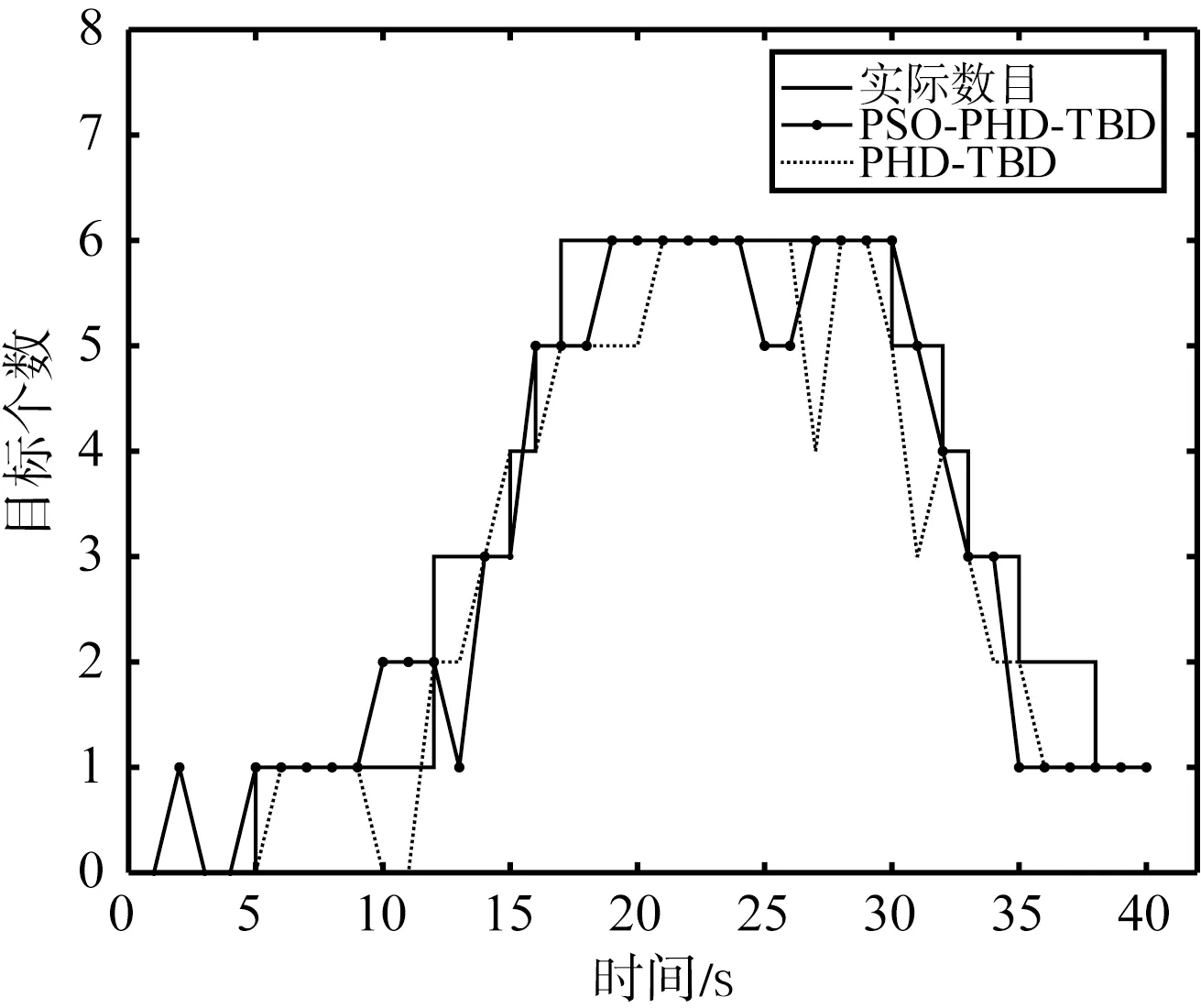
(c) 5 dB的数目估计图3 不同信噪比下算法对目标数目的估计

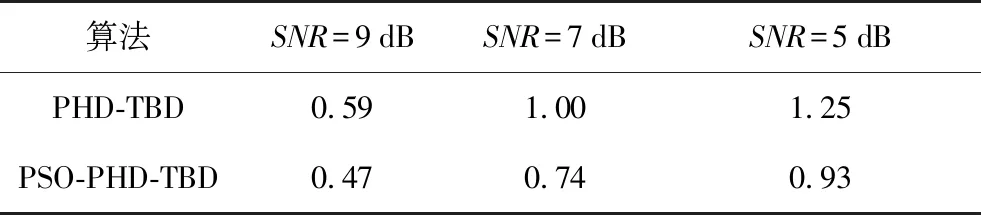
表2 两种算法目标数目估计标准差均值

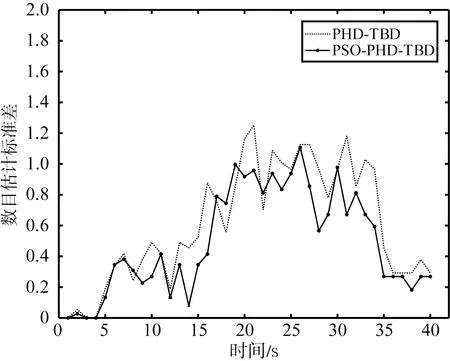
(a) 9 dB的数目估计标准差

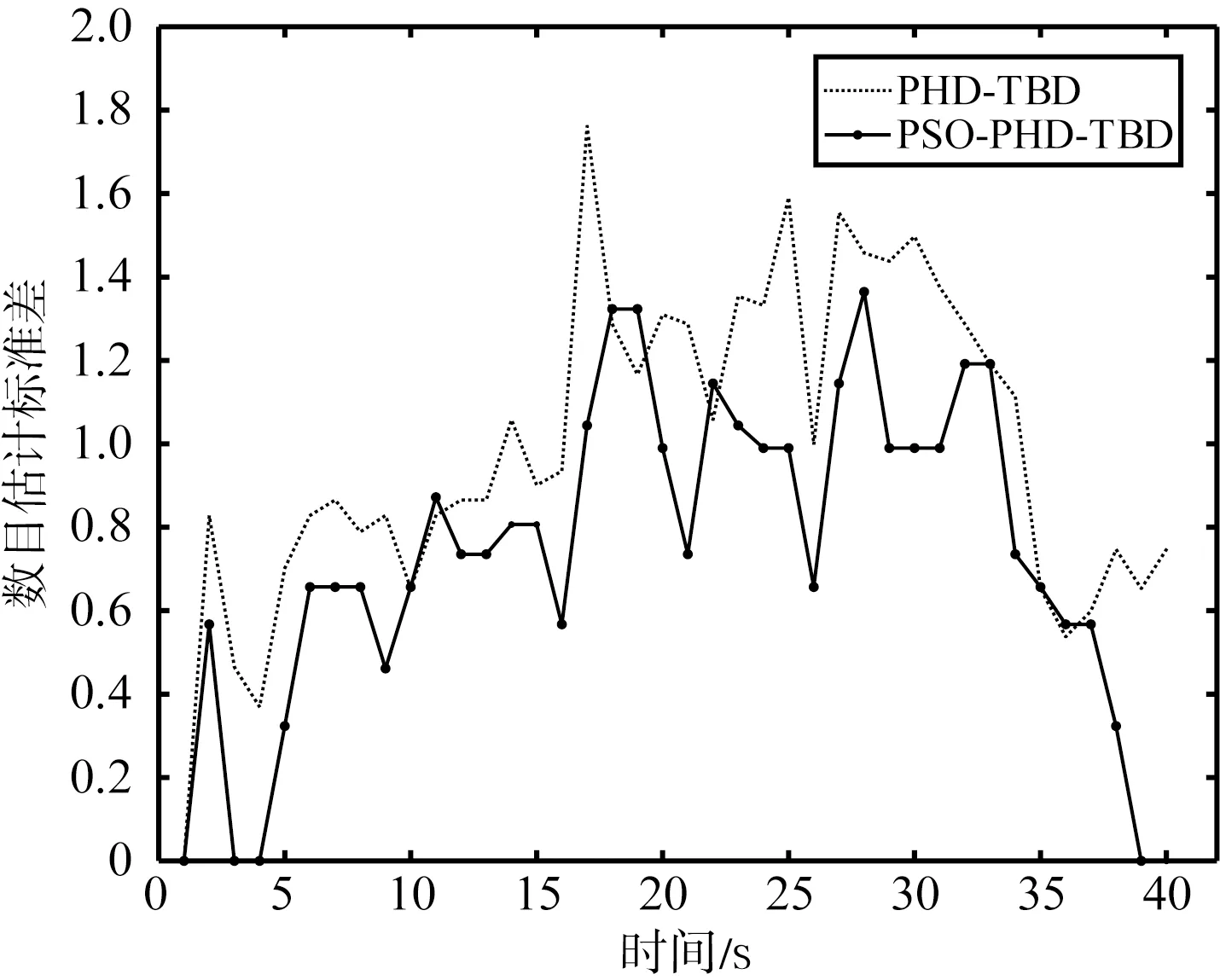
(b) 7 dB的数目估计标准差

(c) 5 dB的数目估计标准差图4 不同信噪比下算法对目标数目估计标准差

2) 对目标位置精度的估计情况

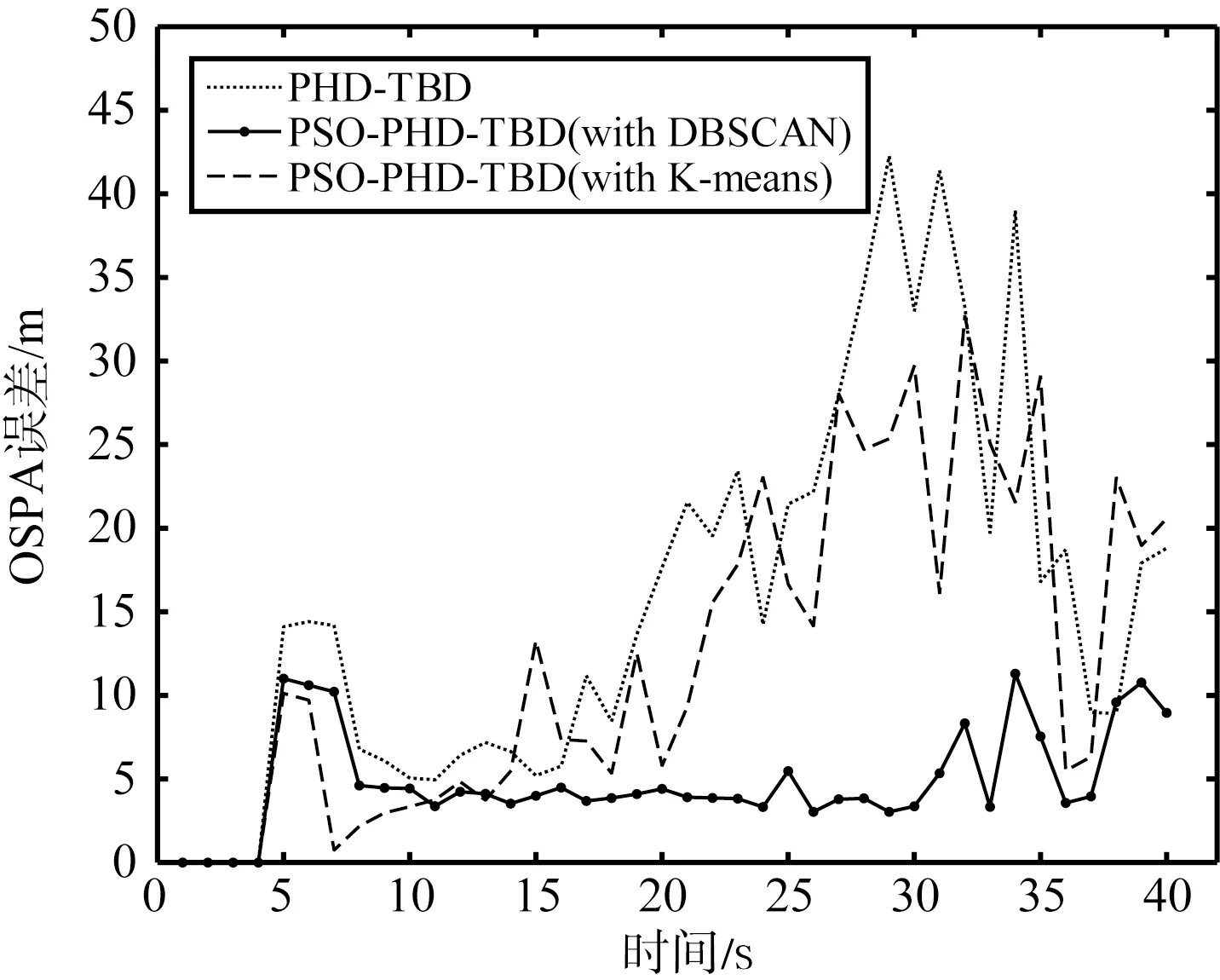
本文按照OSPA距离[24]作为误差评判标准，设置OSPA距离参数截断距离c=50 m，p=2。为了更好地进行对比说明粒子群优化与DBSCAN方法相结合的优势，另外添加了结合粒子群优化但进行常规K-means聚类的PHD-TBD算法添加对照，按照相同的仿真场景，得出的结果如图5所示。具体3种算法在不同信噪比下的OSPA误差的均值如表3所示。

综合来看，新提出的PSO-PHD-TBD算法主要在目标位置估计精度上较PHD-TBD算法有了明显的进步，随着信噪比的降低，精度上优势更加明显。

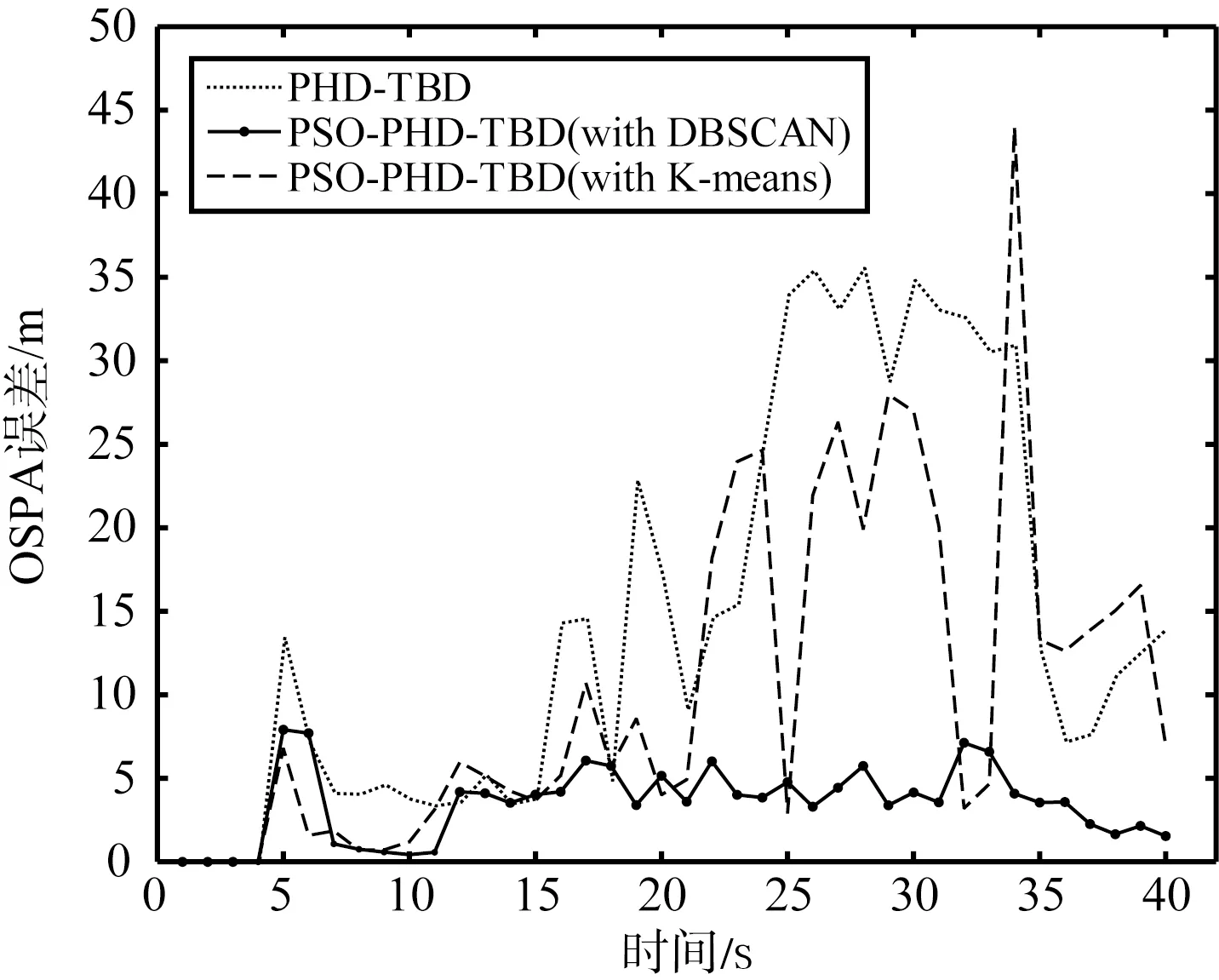
(a) 9 dB的目标位置估计误差

(b) 7 dB的目标位置估计误差

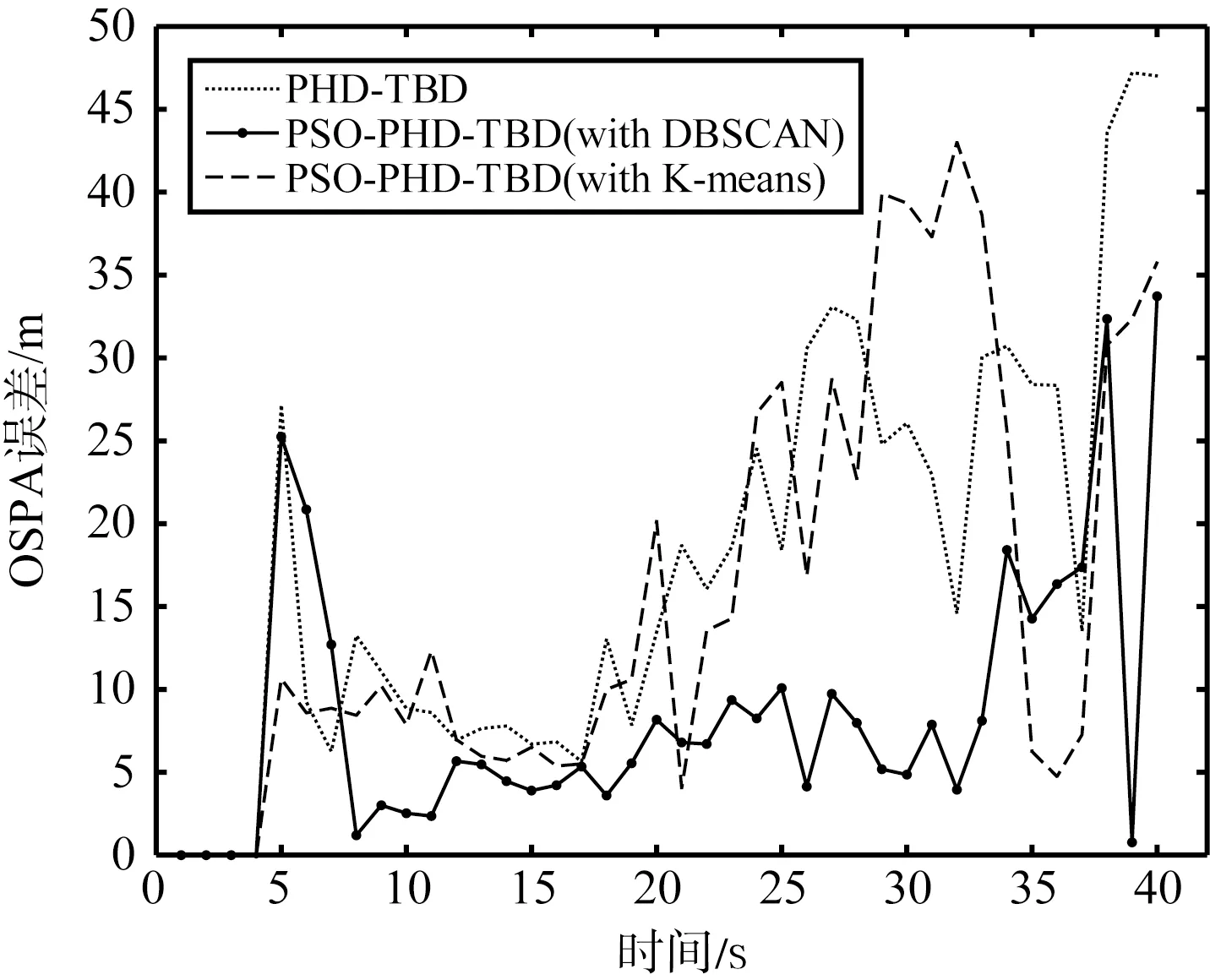
(c) 5 dB的目标位置估计误差图5 不同信噪比下3种算法的误差比较

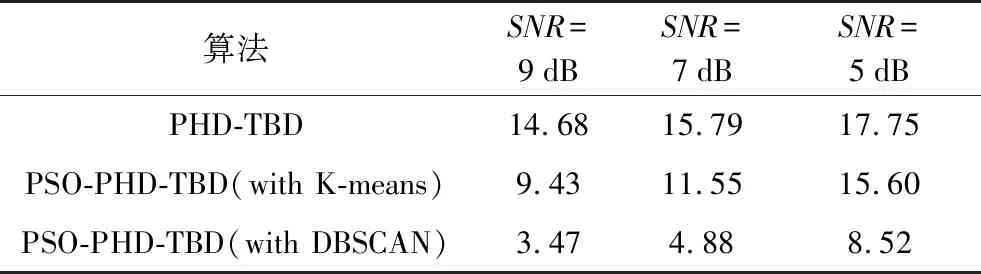
表3 不同信噪比下OSPA误差均值 m

3) 算法实现复杂度分析

本文所提出的PSO-PHD-TBD的粒子滤波实现方式，借助了多目标粒子群优化，DBSCAN算法共同实现。DBSCAN算法的时间复杂度是O(n2)，相比于K-means聚类的时间复杂度O(n)更加复杂，另外基于NSGA-Ⅱ的MOPSO算法的时间复杂度为O(mn2)，其中m为目标函数的个数，n为粒子数目，通过理论分析PSO-PHD-TBD算法运行时间确实更长，最为理想的情况下生存粒子维持现有的分布，仅有新生粒子随着粒子群优化而改变分布，会使得优化所用的时间最短。在Intel(R) Core(TM) i5-4590 3.30 GHz CPU，16 GB(DDR3 1600 MHz)内存，Win7 64位旗舰版计算平台下运行不同信噪比条件下仿真的平均时长如表4所示。

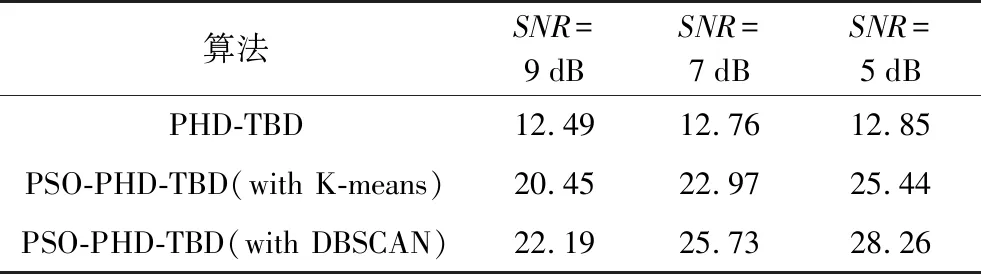
表4 不同信噪比下算法运行时长 s

在信噪比降低的情况下，优化步骤会受到一定的影响，从而PSO-PHD-TBD的运算时间会随之增加，反观PHD-TBD算法因为不存在优化步骤，因此在时间上并没有随信噪比的变化而能明显改变；因为DBSCAN的算法复杂度高于K-means聚类，因此同样经过粒子群优化而聚类不同的算法运算效率也不同，具体而言本文提出的粒子群优化与DBSCAN算法相结合的用时更长。虽然运算成本不可避免地增加，但是很明显的一点是本文提出的PSO-PHD-TBD的算法性能要明显地优于PHD-TBD。在运行时间尚能容忍的情况下，利用DBSCAN聚类的PSO-PHD-TBD算法依旧是更好的选择。

4 结束语

经过仿真对比发现，结合DBSCAN聚类的PSO-PHD-TBD算法通过粒子群优化算法结合量测优化粒子分布，再将基于密度的聚类算法运用到经过优化的粒子滤波当中可以实现较为良好的聚类效果，能够满足检测目标发现其位置的要求，更是能在目标数目准确估计的情况下将估计误差加以降低。但是DBSCAN算法对两个初始参数邻域半径和邻域最小点数还需要根据仿真过程调试，以达到最佳聚类效果。同时粒子群优化算法复杂度较高，在计算中确实牺牲了一部分计算效率，在今后的工作中则需要尽可能地解决粒子数和运算时间之间的矛盾，并希望能够历史信息自适应选择粒子集群优化，避免低效率的优化。