无限元边界条件下有砟轨道的动力响应分析
崔高航 刘学稿

摘 要:为分析列车荷载作用下有砟轨道的动力响应,文章应用ABAQUS有限元软件建立三维路基基床有限元模型,采用无限元边界条件,分析了路基基床在静轮载5,7.5,10,12.5,15t五种情况下,速度分别为60,80,100km/h条件下的动力响应。有限元分析结果表明:(1)随着列车静轮载的增大,基床表层的竖向位移的幅值会逐渐变大,速度越大,静轮载的增加对竖向位移的增加影响越显著;(2)随着列车速度的增大,基床表层的竖向位移的幅值会逐渐变大,静轮载越大,速度的增加对竖向位移的增加影响越显著;(3)随着动荷载与选取点距离的缩短,选取点的竖向位移开始上下振动并逐渐增大,达到幅值后随着动荷载与选取点距离的增加,选取点的竖向位移逐渐恢复并有上下振动的现象。
关键词:铁路路基;动力响应分析;有限元方法;无限元;速度;静轮载
中图分类号:U231+.2 文献标志码:A 文章编号:2095-2945(2019)09-0033-03
Abstract: In order to analyze the dynamic response of ballast track under train load, the finite element model of three-dimensional subgrade foundation bed is established by using ABAQUS finite element software. The finite element model of subgrade foundation bed under static wheel load of 5,7.5,10,12.5,15t is analyzed by using infinite element boundary condition. The dynamic responses are obtained at speeds of 60, 80, 100 km/h, respectively. The results of finite element analysis show that: (1) with the increase of the static wheel load of the train, the amplitude of the vertical displacement on the surface of the foundation bed will gradually increase, and the larger the speed, the more significant the increase of the static wheel load on the increase of the vertical displacement; (2) with the increase of train speed, The amplitude of the vertical displacement on the surface of the foundation bed will gradually increase, and the larger the static wheel load is, the more significant the increase of the velocity will have on the increase of the vertical displacement; (3) with the shortening of the distance between the dynamic load and the selected point, the vertical displacement of the selected point begins to vibrate up and down and gradually increases. After reaching the amplitude, with the increase of the distance between the dynamic load and the selected point, the vertical displacement of the selected point gradually recovers and has the phenomenon of up and down vibration.
Keywords: railway subgrade; dynamic response analysis; finite element method; infinite element; speed; static wheel load
铁路的碎石床轨道,即有砟轨道,因为其良好的排水性、铺设方便、弹性好、易于维修与更换等优点,所以我国的大部分既有铁路采用有砟轨道,在全国各个地区有着广泛的应用。线路纵向地基土厚度及土层性质存在较大差异,加之路堤填料的不均匀性、地下水交替作用及基床病害等问题的存在,铁路路基不均匀沉降不可避免[1]。我们应该重点分析研究在列车运行时由于运行荷载的存在而在路基内部产生的应力、加速度、位移等动力响应场问题[2]。在列车沿轨道运行时,车辆条件、环境地质状况、轨道条件等是影响振动的主要因素[3]。
随着计算机技术的快速发展,数值模拟方法在轨道交通动力响应问题研究方面大量运用。准确模拟应力在连续介质中的传播是动力响应分析问题中最重要的部分。采用有限元分析法建立轨道路基基床有限元模型,模型要取有限的尺寸进行分析,来模拟无限大的区域,采用近似约束边界条件,但是这样会造成动力波在有限元模型边界面上反射,导致计算结果有一定的误差。模型尺寸的大小范围选择更大一些来降低动力波反射带来的影响,计算机的计算量会明显的增加,但是模型尺寸的取值范围的足够大的界定没有明确的规定。采用近似约束边界有限尺寸的模型不能真实反映无限域对有限单元计算区域的影响,只能在一定程度上满足实际工程的需要。人工边界建立的方法很多,但大多数已有的人工边界在理论和使用上都比较复杂。粘性边界、透射边界、旁轴近似边界和粘弹性边界等动力人工边界被相关的专家提出并应用[4]。由于粘弹性动力人工边界[5]具有较高的精度,且能模拟人工边界外半无限介质弹性恢复性能以及良好的频率稳定性,所以在有限元分析中被广泛应用于结构-地基动力相互作用问题的研究。考虑到需要对边界部分再次编程,且其使用过程中涉及较为多的计算,由于未经过试验,计算中使用的一些模型参数本身带有一定的近似性,使得模拟结果的可靠性降低[6]。無限元法和边界元法、薄层单元相比较,其可以不用求解地基土振动基本解,而且可以和有限单元法结合使用统一形式的运动方程去求解,所以在地基土振动问题研究中广泛采用无限元与有限元相结合的方法[7]。
ABAQUS有限元軟件可以使用无限元作为边界条件来模拟无反射的边界。本文将应用ABAQUS有限元软件建立三维路基基床的有限元模型,并使用FORTRAN语言编程进行二次开发,研究有砟轨道铁路机车的速度和轴重对路基基床的动应力响应的影响,并给出合理化的建议。
1 数值分析模型
1.1 模型的尺寸
本论文取纵向计算长度为30m。轨枕下面的道砟层顶面的宽度为3.6m,道砟边坡坡度为1:1.75,道砟的厚度为0.6m;路基顶面宽度为7.9m,路基的边坡坡度为1:1.5,基床表层的厚度为0.7m,基床底层的厚度为2.3m。有限元模型中两钢轨内侧间距为1435mm。钢轨为各向同性的材料,且横断面简化为矩形截面。简化后钢轨轮廓的宽度w为50mm,高度h为155mm。钢轨采用的钢材的密度为7830kg/m3。因此,每米钢轨的质量为m=w×h×?籽=60.6825kg/m (1)模型采用混凝土Ⅲ型轨枕,在建模中把其简化为长方体,长×宽×高为2.60m×0.32m×0.22m。相邻轨枕的中心线间距为0.6m。
1.2 边界条件
模型纵向两端采用无限元单元来模拟。对于直接受力最大的边界面模型底部采取静态边界条件,约束其竖向位移和水平位移。三维路基基床的有限元模型如图1所示。
1.3 荷载作用
本文仅考虑列车竖向荷载的作用,作用在轨道的上面,在轮轨的接触斑上通过施加压力来表示轮轨的相互作用力。采用拟静力法,将列车的荷载简化为均布荷载作用在轨道上,然后逐层传递。
2 模型的验证
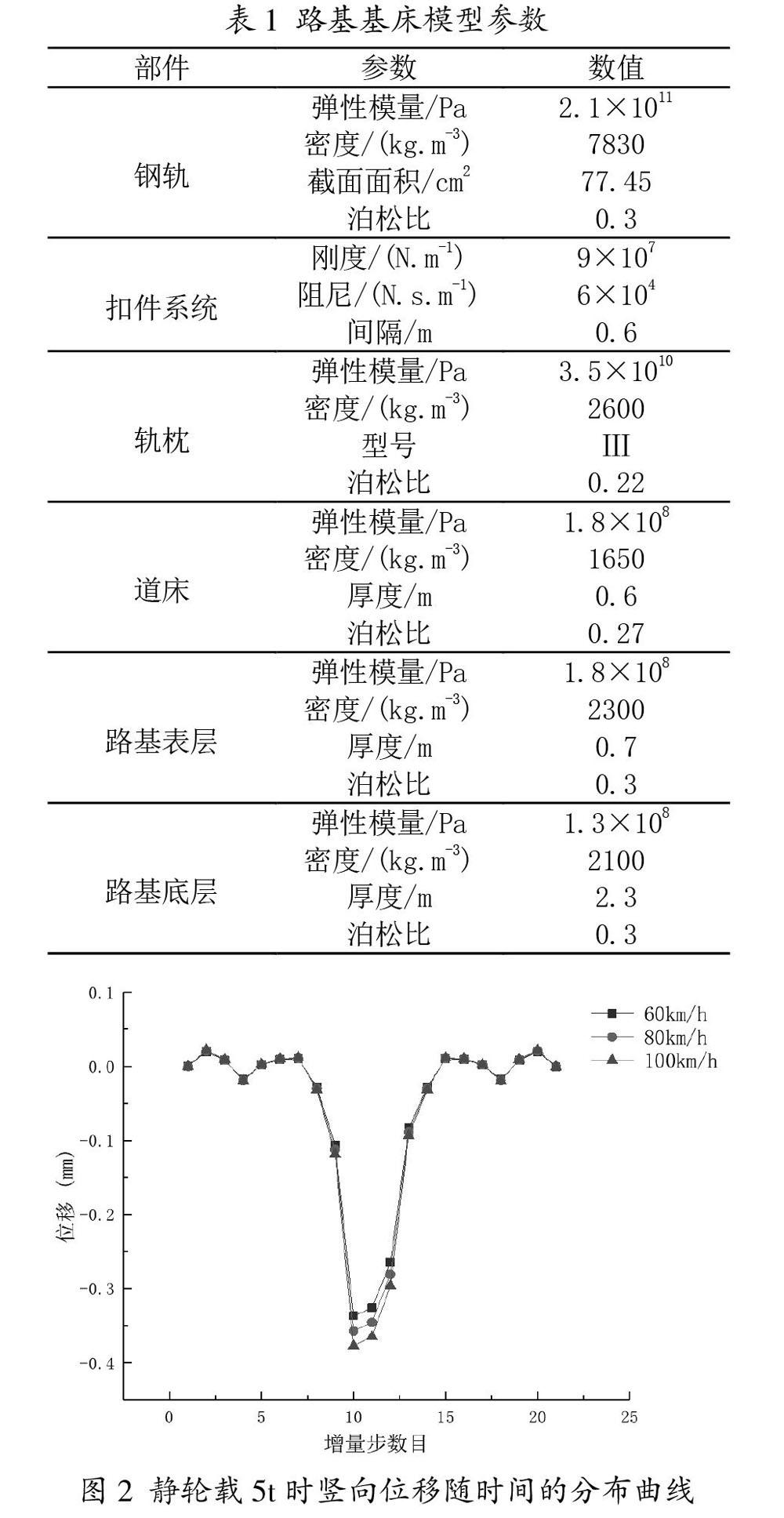
为了验证上述模型的正确性,选择文献[8]的计算结果进行对比分析,将文献中的动力学参数进行对比分析,模型参数如表1。
相同工况的动应力响应对比分析,钢轨的竖向位移幅值,钢轨的竖向加速度幅值,轨枕的竖向位移幅值,轨枕的竖向加速度幅值分别为1.89mm,87.4g,1.07mm,12.28g,文献的计算结果分别为1.91mm,87.35g,1.09mm,12.31g。可见模型的计算值和参考文献的值相差不大,都在5%以内,所以模型是准确可靠的。
3 结论
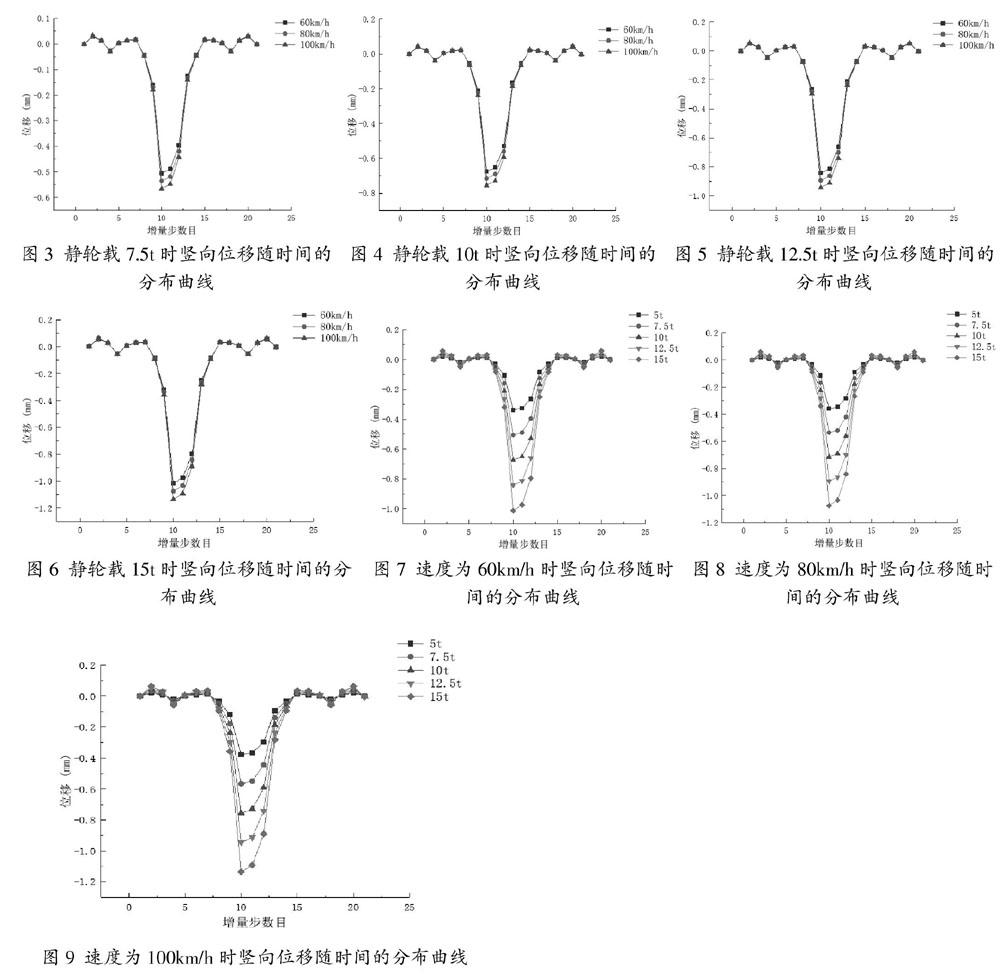
(1)随着列车静轮载的增大,基床表层的竖向位移的幅值会逐渐变大,速度越大,静轮载的增加对竖向位移的增加影响越显著。
(2)随着列车速度的增大,基床表层的竖向位移的幅值会逐渐变大,静轮载越大,速度的增加对竖向位移的增加影响越显著。
(3)随着动荷载与选取点距离的缩短,选取点的竖向位移开始上下振动并逐渐增大,达到幅值后随着动荷载与选取点距离的增加,选取点的竖向位移逐渐恢复并有上下振动的现象。
参考文献:
[1]张群.路基不均匀沉降对双块式无碴轨道的影响研究[D].成都:西南交通大学,2007.
[2]王其昌.高速铁路土木工程[M].成都:西南交通大学出版社,2000.
[3]张玉红,汤卓文,王长林.移动荷载作用下土体动力响应的参数影响分析[J].西安建筑科技大学学报(自然科学版),2011,43(1):44-47.
[4]廖振鹏.工程波动理论导论[M].北京:科学出版社,2002.
[5]Deeks A J,Randolph M F. Axisymmetric time-domain transmitting boundaries[J]. Journal of Engineering Mechanics,1994,120(1):25-42.
[6]陈丽英.高速铁路无砟轨道基础结构的动力响应分析[D].重庆:重庆交通大学,2015.
[7]曹艳梅,王福星,张允士.高速列车作用下场地振动的分析方法及特性研究[J].铁道学报,2017,37(6):118-124.
[8]Jin Shi,Andrew H Chan,Michael PN Burrow. Influence of unsupported sleepers on the dynamic response of a heavy haul railway embankment[J].Journal of Rail and Rapid Transit,2013,227(6):657-667.

