带质量块压电悬臂梁的振动仿真分析

李丽伟 田会珍 李心仪

摘  要：基于压电方程和弹性梁的振动理论，建立了带质量块的单晶悬臂梁压电发电振子的理论模型，运用Ansys仿真分析了质量块对固有频率和输出电压的影响。结果表明：质量块长度与压电振子长度比为1/2左右时压电振子固有频率最小，输出电压出现峰值;固有频率和输出电压随质量块厚度的增加分别呈现减小和增大的趋势;质量块存在一个最佳粘贴位置，使得固有频率最小，输出电压最大。

关键词：压电发电;悬臂梁;质量块;有限元法

中图分类号：TP274 文献标志码：A         文章编号：2095-2945（2019）08-0020-03

Abstract： Based on the piezoelectric equation and the vibration theory of elastic beam， the theoretical model of single crystal cantilever piezoelectric generator with mass block is established. the influence of mass block on natural frequency and output voltage is analyzed by Ansys simulation. The results show that when the ratio of mass block length to piezoelectric vibrator length is about 1/2， the natural frequency of piezoelectric vibrator is the smallest and the output voltage reaches the peak value， and the natural frequency and output voltage decrease and increase with the increase of mass block thickness， respectively. There is an optimal paste position for the mass block， which minimizes the natural frequency and maximizes the output voltage.

Keywords： piezoelectric power generation; cantilever beam; mass block; finite element method

微機电系统（Micro-Electro-Mechanical-System， MEMS）的快速发展，使得便携式低功耗电子产品得到了广泛应用。但目前便携设备主要依靠传统的化学电池供能，存在体积大不利于集成、寿命有限以及制造和使用过程会造成环境污染等诸多问题，迫切需要可持续供电的绿色微能源[1]。近年来，太阳能、风能、环境振动能等可再生能源受到越来越多的关注。其中，在环境中广泛存在的振动能，不受周围温度与光照长短影响，能量获取持续稳定，是锂电池等传统化学电源潜在的替代能源。环境振动能可基于压电[2]、静电[3]及电磁[4]等方式获取，由于压电式悬臂梁发电振子能量获取结构简单、易于微型化与集成，且能量转换密度大，应用前景十分广阔[5-6]。现有的研究多偏重于悬臂梁压电振子压电晶体和弹性基体的结构尺寸参数对发电性能的影响，而环境振动下质量块对压电发电振子输出性能的影响分析较少。本文通过Ansys有限元仿真分析，主要研究质量块对其输出电压和固有频率的影响，以期获得较低的谐振频率和最大的输出电压。

1 悬臂梁压电发电振子的理论建模

悬臂梁式单晶压电发电振子简化结构如图1所示，主要由压电晶体、弹性基体和质量块复合而成。lb、lp、lq分别为悬臂梁、压电晶体和质量块的长度，tm和tp分别为弹性基体和压电晶体的厚度;悬臂梁宽度为w。压电晶体和弹性基体的弹性模量分别为Ep和Em，结构的转动惯量为I。

由小变形弯矩及挠度方程，可得质量块运动微分方程，进而得到压电振子固有频率为：

同时，由压电晶体的本构方程和弹性基体的应力应变方程可得到压电振子在加速度激励Ain下的开路电压为：

2 悬臂梁压电发电振子的有限元仿真

2.1 悬臂梁压电振子的Ansys建模

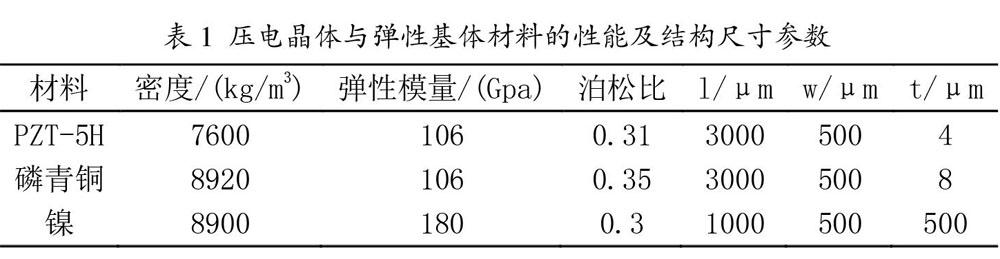
压电复合振子在谐振时输出电压最大，而其固有频率相对于环境振动频率较大，为此采用Ansys仿真分析带质量块的悬臂梁发电振子的质量块长度、厚度和位置对固有频率和输出电压的影响。压电梁材料为PZT-5H，弹性基体材料为磷青铜，质量块材料为镍，压电晶体、弹性基体和质量块的材料性能参数及结构尺寸参数如表1所示。

压电振子质量块端自由，另一端约束所有自由度，压电晶体、弹性基体和质量块采用GLUE命令粘接在一起，均采用扫略方式划分网格，建立压电振子的实体模型。

对悬臂梁施加1g的加速度激励，仿真获得压电振子的一阶固有频率为127.38Hz，同时利用Matlab编程计算理论推导的固有频率为149.74Hz，两者误差为14.9%，表明建立的理论及仿真模型是合理的。

2.2 质量块参数对固有频率和输出电压的影响

（1）质量块长度对固有频率和输出电压的影响

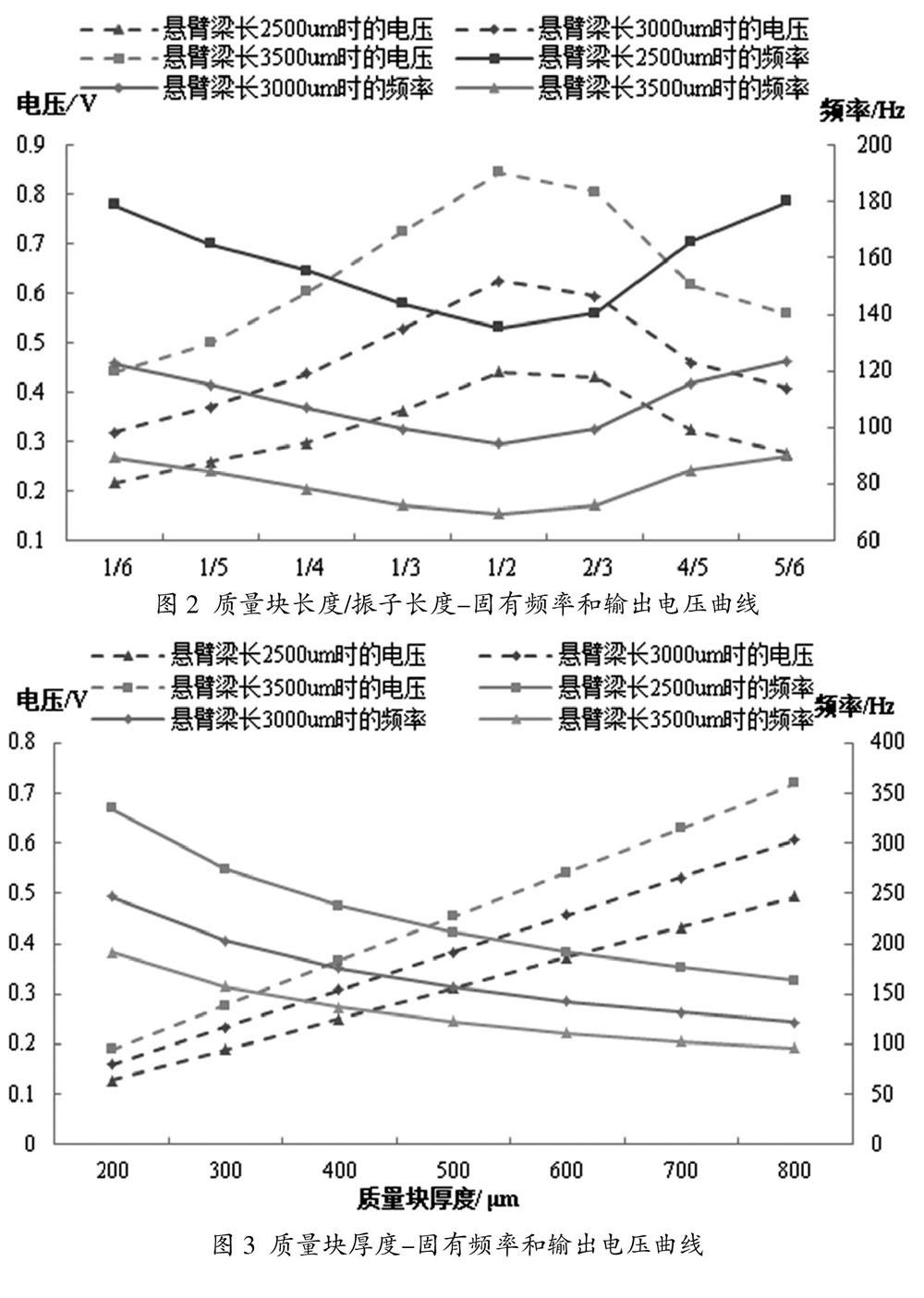
选取压电晶体厚度为4μm，弹性基体厚度为8μm，取压电振子长度分别为2500μm、3000μm、3500μm，改变质量块长度与压电振子长度的比值，分别为1/6、1/5、1/4、1/3、1/2、2/3、4/5、5/6，获得图2所示不同长度下振子固有频率和输出电压与质量块长度的关系。

由图2可知，压电振子的固有频率随质量块长度的增加先减小后增大，且在质量块长度与压电振子长度比为1/2左右时频率最小，而输出电压随质量块长度的增加先增大后减小。由频率f、结构刚度K和质量m的关系f∝K/m可知，当刚度不变时，频率随质量的增大而减小，但当质量块过大时，结构刚度会大大增加，因此压电振子固有频率增大。适当增加质量块长度，可以增大压电振子自由端位移，输出电压也会增大，但当质量块继续增大，自由端位移减小，输出电压也减小。

（2）质量块厚度对固有频率和输出电压的影响

取悬臂梁压电振子长度分别为2500μm、3000μm、3500μm，改变质量块厚度，分别为200μm、300μm、400μm、500μm、600μm、700μm、800μm，获得如图3所示不同长度下振子固有频率和输出电压随质量块厚度变化关系。

由图3可知，压电振子的固有频率随质量块厚度的增加逐渐减小，而输出电压随质量块厚度的增加逐渐增大。原因在于：当质量块厚度增加时，压电振子在激励作用下振动的尖端位移逐渐增大，导致角频率逐渐减小，因此固有频率随着质量块厚度的增加明显减小。同时，尖端位移的增加使结构应力增加，输出电压逐渐增大，因此应尽量选择较厚的质量块。然而，较厚的质量块质量也会显著增加，应尽量避免压电振子在质量块自身重力作用下弯曲过大。

（3）质量块位置对固有频率和输出电压的影响

基于图2和图3的分析，取质量块长度和悬臂梁长度比值为1/3，即当悬臂梁长为3000μm时，质量块长为1000μm，取其厚度为500μm。改变质量块到固定端的距离，取值分别为：2000μm、1800μm、1600μm、1400μm、1200μm、

1000μm、800μm、600μm，保持其它参数不变，获得如图4所示振子固有频率和输出电压随质量块位置变化关系。

由图4可知，随着质量块到固定端位置的逐渐减小，压电振子固有频率逐渐增大，输出电压逐渐减小，即当质量块在自由端端部时，压电振子固有频率最小，输出电压最大。因此，为了获取最大的谐振频率下的输出电压，应尽量将质量块粘贴在压电振子自由端的端部。

3 结束语

本文针对带质量块的单晶悬臂梁压电发电振子，建立了理论模型，仿真分析了质量块的结构和位置参数对发电振子固有频率和输出电压的影响，获得如下结论：

（1）压电振子的固有频率随质量块与振子长度比的增加先减小后增大，且在质量块长度与压电振子长度比为1/2左右时频率最小，而输出电压随质量块长度的增加先增大后减小。

（2）压电振子的固有频率随质量块厚度的增加逐渐减小，而输出电压随质量块厚度的增加逐渐增大。

（3）随质量块距固定端的距离的增大，压电振子的固有频率逐渐减小，输出电压逐渐增大。因此将质量块设置在自由端更易适应低频环境振动。

参考文献：

[1]孙谦晨，周健，叶金晶，等.基于光伏电池供能的微能源模块设计与仿真[J].电源技术，2018，42（09）：1374-1375+1407.

[2]成立，李茂军，王鼎湘，等.基于压电效应的风力发电方法研究[J].压电与声光，2015，37（02）：361-364.

[3]王威，马爽，韩都，等.静电纺丝法制备服装用PVDF压电传感器[J].仪表技术与传感器，2017（10）：123-126.

[4]杜小振，曾祥伟，卞丰，等.MEMS自供能压电电磁集成发电研究现状[J].微纳电子技术，2014，51（03）：161-167.

[5]张允，王战江，蒋淑兰，等.振动能量收集技术的研究现状与展望[J].机械科学与技术，2018：1-31.

[6]Schaijk R V， Elfrink R ， Oudenhoven J ， et al. A MEMS vibration energy harvester for automotive applications[J]. Proceedings of the Spie， 2013，8763：876305-876305-10.

[7]賀学锋，李江，赵兴强，等.带质量块的微型压电式风能采集器研究[J].传感技术学报，2011，24（07）：986-989.