各向异性地层井壁破裂压力预测
马天寿, 唐 弢, 陈 平, 陈春宇, 孙少林, 刘 阳
(1.西南石油大学油气藏地质及开发工程国家重点实验室,四川成都 610500;2. 中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室,湖北武汉 430071;3.中国石油长庆油田公司油气工艺研究院,陕西西安 710018; 4.中国石油西部钻探克拉玛依钻井公司,新疆克拉玛依 834009)
地层破裂压力是钻井工程设计、钻井液密度优化、钻井措施制定的重要基础[1-5],同时,也是水力压裂设计、压裂设备选择、压裂施工措施制定的重要依据[6-7]。国内外学者针对直井破裂压力预测开展了深入研究,形成了多种经验模型和解析模型[8-13],但绝大部分模型都假设岩石是各向同性连续介质[14-15]或横观各向同性连续介质[16-25],对任意产状各向异性条件下的直井井壁破裂力学机制研究较少。为此,笔者基于Lekhnitskij[26]和Amadei[27]求解各向异性介质平面孔口问题的方法,建立考虑各向异性的直井井壁破裂压力预测模型,分析破裂压力的影响因素,以揭示各向异性地层井壁破裂的力学机制,为实际工程设计和施工措施制定提供指导。
1 井周应力分布模型建立
1.1 岩石各向异性力学特性
为了准确认识各向异性岩石力学特性,收集了多种不同页岩的各向异性弹性模量数据[28-37],并绘制了页岩纵向和横向弹性模量交汇图,如图1所示。不难看出,平行层理方向弹性模量E与垂直层理方向弹性模量E′存在显著差异,E>E′,且比值大都高于1.5,部分超过2.0,说明页岩各向异性特征较为显著。

图1 不同类型页岩纵向和横向弹性模量交汇图Fig.1 Cross-plot of longitudinal and transverse elastic modulus for different shale rocks
1.2 模型建立
为简化模型建立过程,假设:地层为横观各向同性介质;地层均匀且连续;岩石变形满足弹性变形及小变形假设;井周应力应变满足广义平面应变;忽略渗流、温度和钻井液化学作用的影响。
对任意层理产状下的垂直井眼,应力分布模型涉及5个坐标系(图2):①整体坐标系(xyz),也称大地坐标系;②地应力坐标系(xsyszs),最小水平地应力与北坐标夹角为βs;③井眼坐标系(xbybzb),与地应力坐标系重合;④圆柱坐标系(rbθbzb);⑤地层坐标系(xwywzw),指地层中层理面的局部坐标系,层理的倾角为αw和倾向为βw。

图2 不同坐标系之间的转换关系Fig.2 Transformation relations between different coordinate systems
地层局部坐标系下,岩石的本构方程为
{ε}xwywzw=[A]{σ}xwywzw,
(1)
其中
式中,{σ}xwywzw和{ε}xwywzw分别为地层坐标下的应力和应变矢量;[A]为岩石柔度矩阵;E和v分别为平行于层理面弹性模量和泊松比;E′、v′和G′分别为垂直于层理面弹性模量、泊松比和剪切模量。
在井眼坐标系下求解应力分布,需采用井眼坐标系下的有效柔度矩阵,根据图2所示关系,可得井眼坐标系下应力-应变关系为
{ε}xyz=[AT]{σ}xyz,
(2)
其中
[AT]=[Mσ]T[A][Mσ].
式中,{σ}xyz和{ε}xyz分别为井眼坐标系下的应力和应变矢量;[AT]为井眼坐标系下柔度矩阵;[Mσ]为地层坐标系与整体坐标系之间的应力转换矩阵。
根据广义平面应变假设,εz=0,由式(2)可得:
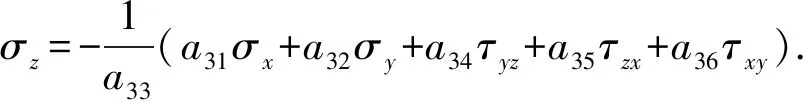
(3)
式中,aij为柔度矩阵[AT]的分量,i、j=1,2,3,4,5,6;σx、σy、σz、τxy、τyz和τzx为应力分量。
结合平衡方程、几何方程和协调方程,根据Lekhnitskij[26]和Amadei[27]求解各向异性平面孔口问题的解法,求解出解析函数表示的应力分量[21]为
(4)
式中,φk(zk)为解析函数,k=1,2,3;zk为复变量,zk=x+μky;μk为与应变协调方程对应的特征方程特征根;λk为与特征根有关的系数。
式(4)即为井周应力分布问题的控制方程,井周应力分布问题的求解已经转换为3个解析函数的求解,须结合边界条件进行求解。
1.3 应力分布解
根据井眼周围的受力边界条件可知,井眼周围地层受到原地应力、井筒压力的影响,采用叠加原理可将应力分布分为3部分[26-27]:井眼钻开前作用的原地应力分量、井眼形成引起的应力分量、井壁流体压力引起的应力分量。
(1) 井眼钻开前作用的原地应力分量。井眼钻开前,井周应力分量即远场原地应力分量,通常采用水平和垂向地应力进行描述,即
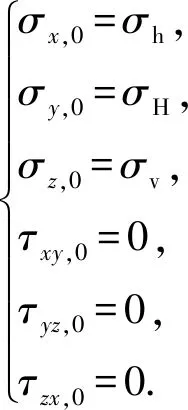
(5)
式中,σH、σh和σv分别为最大、最小水平地应力和垂向应力;σx,0、σy,0、σz,0、τxy,0、τyz,0和τzx,0为井眼钻开前原地应力作用下的应力分量。
(2) 井眼形成引起的应力分量。对于不考虑内压的情况,井眼形成后井壁应力为0,则对井壁上任意点(a,θ),其边界条件为
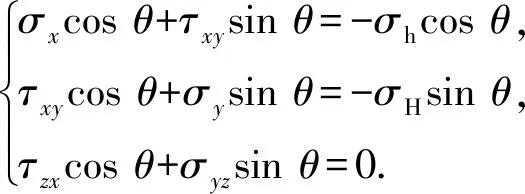
(6)
将式(4)带入式(6)可求解得到3个解析函数,将解析函数带入式(4),得井壁流体压力引起的应力分量表达式为

(7)
其中
b2=-Re[iγ1(λ2λ3-1)+iγ2(1-λ1λ3)+
iγ3λ3(λ1-λ2)],
b3=+Re[iγ1λ1(λ2λ3-1)+iγ2λ2(1-λ1λ3)+
iγ3(λ1-λ2)],
b4=-Re[iγ1μ1λ1(λ2λ3-1)+iγ2μ2λ2(1-λ1λ3)+
iγ3μ3(λ1-λ2)],
b5=+Re[iγ1μ1(λ2λ3-1)+iγ2μ2(1-λ1λ3)+
iγ3μ3λ3(λ1-λ2)],
c2=-Re[γ1(μ2-μ3λ2λ3)+γ2(λ1λ3μ3-μ1)+
γ3λ3(μ1λ2-μ2λ1)],
c3=+Re[γ1λ(μ2-μ3λ2λ3)+γ2λ2(λ1λ3μ3-μ1)+
γ3(μ1λ2-μ2λ1)],
c4=-Re[γ1μ1λ1(μ2-μ3λ2λ3)+γ2μ2λ2(λ1λ3μ3-
μ1)+γ3μ3(μ1λ2-μ2λ1)],
c5=+Re[γ1μ1(μ2-μ3λ2λ3)+γ2μ2(λ1λ3μ3-
μ1)+γ3μ3λ3(μ1λ2-μ2λ1)],
Δ=(μ2-μ1)+λ2λ3(μ1-μ3)+λ1λ3(μ3-μ2),
zk=a(cosθ+μksinθ).
式中,σx,h、σy,h、σz,h、τxy,h、τyz,h和τzx,h为井眼钻开引起的应力分量;a为井眼半径;θ为井周角。
(3) 井壁流体压力引起的应力分量。对于只考虑井筒内钻井液液柱压力的情况,井壁作用的法向应力为液柱压力pm,则对井壁上任意点(a,θ),其边界条件为
(8)
将式(4)带入式(8)可求解得到3个解析函数,将解析函数带入式(4),得井壁流体压力引起的应力分量表达式[38]为
(9)
其中
d2=+Re[γ1(μ2-μ3λ2λ3+iλ2λ3-i)+γ2(λ1λ3μ3-μ1+
i-iλ1λ3)+γ3λ3(μ1λ2-μ2λ1+iλ1-iλ2)],
d3=-Re[γ1μ1(μ2-μ3λ2λ3+iλ2λ3-i)+γ2μ2(λ1λ3μ3-
μ1+i-iλ1λ3)+γ3μ3λ3(μ1λ2-μ2λ1+iλ1-iλ2)],
d4=+Re[γ1λ1μ1(μ2-μ3λ2λ3+iλ2λ3-i)+
γ2λ1μ2(λ1λ3μ3-μ1+i-iλ1λ3)+γ3μ3(μ1λ2-
μ2λ1+iλ1-iλ2)],
d5=-Re[γ1λ1(μ2-μ3λ2λ3+iλ2λ3-i)+γ2λ1(λ1λ3μ3-
μ1+i-iλ1λ3)+γ3(μ1λ2-μ2λ1+iλ1-iλ2)].
式中,σx,b、σy,b、σz,b、τxy,b、τyz,b和τzx,b为井眼钻开后井筒压力作用下的应力分量。
根据叠加原理,将上述3个应力分量进行叠加可得到井周总应力模型为
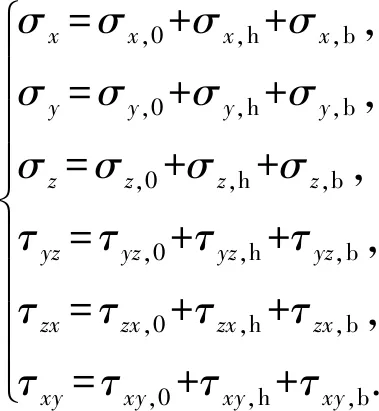
(10)
2 破裂压力计算方法
2.1 拉伸破坏准则
井壁破裂是由于井壁张应力超过岩石强度所致。拉伸破坏取决于地层岩石的抗张强度St,若考虑孔隙压力影响,拉伸破坏准则可写为
σ3-αpp=-|St|.
(11)
式中,σ3为井壁拉伸主应力;St为岩石的抗张强度;α为Biot系数;pp为孔隙压力。
2.2 井壁破裂压力
计算破裂压力要先计算出井眼圆柱坐标下应力分量,并将其带入式(11),可得到井壁破裂压力。根据图2所示坐标关系,通过转轴公式变换,可得圆柱坐标下井壁应力分量为
(12)
直井井壁破裂主要是由井壁环向应力超过岩石抗张强度所致,井壁张应力为min{σθ},则有:
σ3-αpp=min{σθ}-αpp=-|St|.
(13)
联立式(12)和(13),对式(13)进行迭代求解,可得到井壁破裂时的临界井筒压力。
3 破裂压力影响因素
根据破裂压力计算方法可知,破裂压力与层理产状、地应力、孔隙压力等因素密切相关,为了明确这些因素对破裂压力的影响,选取四川盆地XX井数据进行参数敏感性分析,该井的基础参数为:垂深2 500 m、井眼尺寸215.9 mm、垂向地应力61.2 MPa、最小水平地应力47.6 MPa、最大水平地应力55.5 MPa、最小水平地应力方位0°、孔隙压力30.5 MPa、平行层理方向弹性模量47.0 GPa、垂直层理方向弹性模量23.5 GPa、泊松比0.22、Biot系数0.80、抗张强度6.35 MPa。
3.1 层理产状的影响
为了揭示层理产状(倾斜方位和倾角)对破裂压力的影响,分别计算不同产状下的破裂压力,E/E′=2.0,结果如图3所示。为了简洁直观地展示,此处采用了半球投影图表达计算结果,图3中同心圆代表不同倾角、径向射线代表不同倾斜方位,而破裂压力表示为钻井液当量密度。不难看出:①各向同性模型计算破裂压力为2.824 g/cm3,这与水平层理或低角度层理计算结果一致,即图3中A点,说明低角度层理对破裂压力影响较小,基本可以忽略;②当倾斜方位沿着最小水平地应力方向时,破裂压力随倾角增加而增加,最高破裂压力为3.031 g/cm3,破裂压力最大增幅约为0.207 g/cm3,如图3中AB方向,说明钻井井壁发生破裂的风险降低,有利于井壁稳定,但不利于水力压裂,此时井壁破裂压力变化的主要原因是井壁环向拉伸应力逐渐降低,如图4(a)所示;③当倾斜方位沿着最大水平地应力方向时,破裂压力随倾角的增加,先降低后略微增加,最低破裂压力为2.695 g/cm3,破裂压力最大降幅约为0.129 g/cm3,如图3中AD方向,说明钻井过程中井壁发生破裂的风险增加,不利于井壁稳定,但有利于水力压裂,此时井壁破裂压力变化主要是由于井壁环向拉伸应力出现了先增加后略微降低的变化趋势,如图4(c)所示;④在倾角相同的情况下,随着倾斜方位由最小水平地应力偏向最大水平地应力,井壁破裂压力逐渐降低,其中接近垂直的高角度层理将导致较大的变化,破裂压力由3.031 g/cm3降低至2.745 g/cm3,降低幅度约为0.286 g/cm3,如图3中BCD路径;井壁破裂压力变化主要原因是井壁环向应力分布规律在各向异性的控制下发生了极为显著的变化,环向应力由较为规则“哑铃”形状逐渐变为不规则“哑铃”形状,如图4(b)箭头所示,而且井壁最大拉伸应力逐渐增加。

图3 层理产状对破裂压力的影响Fig.3 Influence of bedding occurrence on fracture pressure
3.2 弹性模量各向异性程度的影响
为了揭示岩石弹性模量各向异性对破裂压力的影响,分别计算弹性模量各向异性系数E/E′为1.0、1.5、2.0和2.5时的破裂压力,计算结果如图5所示,其中E/E′=2.0情况下的计算结果如图3所示。由图5可以看出:①在各向同性(E/E′=1.0)情况下,破裂压力与层理产状无关,如图5(a)所示;在各向异性(E/E′≠1.0)情况下,破裂压力与层理产状关系密切且整体变化规律基本一致,层理倾斜方位与最小水平地应力方向一致情况下的破裂压力最高,而与层理倾斜方位与最大水平地应力方向一致情况下的破裂压力最低,如图3和图5(b)、(c)所示;②随着各向异性程度的增加,除了低角度层理的破裂压力不发生变化,其余层理在相同产状下得到的破裂压力数值存在明显差异,破裂压力的最高值逐渐增加,同时破裂压力的最低值也逐渐降低,如图3和图5(b)、(c)所示;③朝着最小水平地应力倾斜的垂直层理破裂压力最高,各向异性系数为1.5、2.0和2.5情况下最高破裂压力分别为2.937、3.031和3.058 g/cm3,对应破裂压力最大增幅约为0.113、0.207和0.234 g/cm3;④朝着最大水平地应力倾斜的高角度层理破裂压力最低,各向异性系数1.5、2.0和2.5情况下最低破裂压力分别为2.755、2.695和2.642 g/cm3,对应破裂压力最大降幅约为0.069、0.129和0.182 g/cm3。说明随着弹性模量各向异性程度的增强,对井壁破裂压力的影响逐渐增强,弹性各向异性的影响不应被忽略。

图4 层理产状对环向应力的影响Fig.4 Influence of bedding occurrence on hoop stress

图5 弹性模量各向异性程度对破裂压力的影响Fig.5 Influence of degree of anisotropy in elastic modulus on fracture pressure
3.3 泊松比各向异性程度的影响
为了揭示泊松比各向异性的影响,分别计算泊松比各向异性系数v/v′为1.0、1.5、2.0和2.5时的破裂压力,计算结果如图6所示,其中v/v′=1.0情况下的计算结果如图3所示。由图6可以看出:①泊松比各向异性对破裂压力具有一定影响,主要结果是导致破裂压力与层理产状关系发生显著变化,对最高和最低破裂压力数值的影响较小,最高值约为3.05 g/cm3,而最低值约为2.70 g/cm3;②在层理倾斜方位沿着最小水平地应力方向的情况下,随着各向异性系数的增加,破裂压力变化规律由最初的逐渐增加演变为逐渐降低并增加,最大值仍然出现在最小水平地应力方向;③在层理倾斜方位沿着最大水平地应力方向的情况下,随着各向异性系数的增加,破裂压力仍然保持逐渐降低并略微增加的变化趋势;④在层理倾角相同的情况下,随着倾斜方位由最小水平地应力偏向最大水平地应力时,破裂压力变化规律由最初的逐渐降低演变为先增加后降低的趋势,尤其是在各向异性较强时,最大和最小水平地应力中间出现了非常明显的破裂压力增加。
3.4 地应力的影响
为了分析地应力对破裂压力的影响,分别计算水平地应力比值σH/σh为1.2、1.6、2.0时的井壁破裂压力,计算时固定σh而改变σH,结果如图7所示。由图7可以看出:①破裂压力随层理产状变化基本能够保持一致,即层理倾斜方位与最小水平地应力方向一致情况下破裂压力最高,而与层理倾斜方位与最大水平地应力方向一致情况下破裂压力最低;②随着水平地应力比值的增加,破裂压力整体上呈减小趋势,即水平地应力差异越大,破裂压力越低,3种情况下各向同性地层的破裂压力分别为2.758、1.981和1.205 g/cm3,越不利于井壁稳定,却有利于水力压裂裂缝的起裂;③随着水平地应力比值的增加,破裂压力变化幅度逐渐变大,即破裂压力降幅和增幅均显著增加。例如,朝着最小水平地应力倾斜的垂直层理破裂压力最高,3种情况下最高破裂压力分别为2.992、2.528和2.065 g/cm3,与各向同性地层相比,对应破裂压力最大增幅约为0.234、0.547和0.860 g/cm3。朝着最大水平地应力倾斜的高角度层理破裂压力最低,3种情况最低破裂压力分别为2.605、1.550和0.495 g/cm3,与各向同性地层相比,对应破裂压力最大降幅约为0.153、0.431和0.710 g/cm3,其降幅甚至超过了50%,说明水平地应力差值增加的同时,各向异性的影响也进一步加剧,此外地应力对破裂压力变化值的影响明显要高于地层各向异性产生的影响,即地应力是地层破裂压力的主控因素。
3.5 孔隙压力的影响
孔隙压力对破裂压力也具有明显的影响,为了分析其在考虑各向异性后的影响,计算孔隙压力梯度分别为1.0、1.2和1.4时的破裂压力,结果如图8所示。由图8可以看出:①不考虑各向异性影响时,当孔隙压力由25 MPa增加至35 MPa,各向同性地层破裂压力由3.019 g/cm3降低至2.700 g/cm3,说明孔隙压力越高破裂压力越低,井壁稳定性越差;②考虑各向异性影响后,3种情况下的破裂压力随层理产状变化规律基本保持一致,即层理倾斜方位与最小水平地应力方向一致情况下破裂压力最高,而与层理倾斜方位与最大水平地应力方向一致情况下破裂压力最低;③随着水平地应力比σH/σh的增加,破裂压力的变化幅度逐渐变大,即破裂压力降幅和增幅均显著增加。例如,朝着最小水平地应力倾斜的垂直地层破裂压力最高,3种情况下最高破裂压力分别为3.238、3.069和2.899 g/cm3,与各向同性地层相比,破裂压力最大增幅约为0.219、0.209和0.199 g/cm3;朝着最大水平地应力倾斜的高角度层理破裂压力最低,3种情况下最低破裂压力分别为2.893、2.735和2.576 g/cm3,与各向同性地层相比,破裂压力最大降幅约为0.126、0.125和0.124 g/cm3,这说明孔隙压力增加的同时,各向异性的影响略微降低,孔隙压力也是地层破裂压力的重要影响因素。
4 结 论
(1)考虑各向异性影响后,破裂压力随层理产状变化,低角度层理对破裂压力影响较小,沿最小水平地应力方向倾斜的高角度层理,其破裂压力最高,而沿最大水平地应力方向倾斜的高角度层理,其破裂压力最低。
(2)弹性模量各向异性影响下,不同层理产状的分布规律大致相似,但破裂压力数值变化显著,随着各向异性程度的增加,破裂压力最高值逐渐增加,而最低值逐渐降低,说明其对破裂压力的影响逐步加剧;泊松比各向异性影响下,层理产状的影响规律发生了显著变化,但破裂压力变化不明显。
(3)随着水平地应力比增加,破裂压力整体上呈减小趋势变化,地应力的影响明显高于岩石各向异性,说明地应力是地层破裂的主控因素;随着水平地应力比的增加,破裂压力变化幅度逐渐增加,说明各向异性的影响逐渐加剧;随着孔隙压力的增加,不同层理产状的分布规律大致相似,破裂压力整体上呈减小趋势,但破裂压力变化幅度基本不变。

