带非线性约束的自适应高斯和卡尔曼滤波目标跟踪算法

(江南大学 物联网工程学院, 江苏 无锡 214122)

0 引言

无线传感网络中运动目标状态估计与跟踪已广泛运用到诸多领域,例如无人飞行器的边界监视[1]、多移动机器人目标跟踪[2]以及太空监测[3]等等。贝叶斯框架是研究这些动态系统常用的方法,从贝叶斯理论得到的状态后验密度中可以得到目标当前时刻状态的完整统计[4]。

卡尔曼滤波常用于基于状态过程和测量模型来估计动态系统的状态。如果运动目标的动态状态空间模型(dynamic state-space model, DSSM)与加性高斯噪声是线性的并且噪声统计特性是服从高斯分布的,那么对于这种特殊情况,卡尔曼滤波器能够在最小均方误差(minimum mean square error, MMSE),最大似然(maximum likelihood, ML)和最大后验概率(maximum a posteriori, MAP)意义下产生最优解[4-5]。

然而,随着实际情况中越来越多的复杂要求,经典卡尔曼滤波估计会遇到以下两个难点:首先,动态系统的实际过程和测量模型通常是非线性的,其次,过程噪声和测量噪声经常是是非高斯的[6]。因此卡尔曼滤波器可能会无法得到有效的状态估计。

高斯和滤波器(gaussian sum filter, GSF)以及粒子滤波器(Particle Filter ,PF)常被用于解决非线性、非高斯系统的状态估计问题。GSF使用高斯分布的加权和来逼近状态概率密度函数,同时可以近似任意分布[6]。但是传统高斯和滤波器存在严重的局限性,即每次迭代时用于近似密度函数的高斯项的数量都会增加。经过许多学者的研究扩展,提出了一种改进的估计算法。其本质是将唯一描述每个高斯项的参数向量加上某种限制规则。一种方案是使高斯项的每次迭代都从有限组已知值中随机选择[6-8];另一种则是对高斯子项的数量上限设置一个阈值。因此滤波器每次迭代的高斯项的数量将被固定,从而避免了项数增长的累积问题[9-12]。

当一个运动系统的约束无法被引入滤波器的结构之中时,该约束信息常常会被忽视或做近似处理[13]。譬如在WSN中要实现地面目标跟踪,目标的运行轨道大多数情况下是已知的。但雷达的观测轨迹由于测量中的噪声和杂波而显示出失真情况。如果不使用这些关于状态约束的附加信息,那么用卡尔曼滤波器得到的估计,也仅仅是因为使用了一组不完全的信息而得到的伪最优估计。

文献[13]对目前的约束卡尔曼滤波做了很好的归纳总结。文献[14]提出了一个严格的分析方法,将等式约束纳入卡尔曼滤波过程。首先是获得无约束卡尔曼滤波解,然后将无约束状态估计投影到约束曲面上。Teixeira和Torres等人提出的算法是将非线性等式约束并入无迹卡尔曼滤波(unscented kalman filter, UKF)过程,来解决非线性系统的状态估计问题。其中包括PUKF、ECUKF和MAUKF3种算法[15-16]。

为了解决传统约束卡尔曼滤波方法对非线性、非高斯系统状态估计精度低等问题,本文提出一种带非线性等式约束的自适应高斯和卡尔

曼滤波算法,可用于WSN中非高斯噪声背景下的运动目标跟踪。通过引入自适应高斯和滤波策略,解决了传统高斯和滤波器中的项数增长问题,提高了跟踪精度与稳定性。

1 相关工作

1.1 系统模型

假设无线传感网络中的某个运动目标的系统状态和观测模型满足下式:

xk+1=f(xk,wk)

(1)

zk=h(xk,vk)

(2)

其中,xk∈x为系统在k时刻的状态矢量,zk∈z为k时刻的观测矢量,wk和vk分别为非高斯的过程噪声和测量噪声,f(·)和h(·)分别为已知的状态函数和观测函数。

滤波的本质即基于每个k时刻的量测Zk={z1,...zk}来得到状态矢量xk的后验概率密度p(xk|Zk),则基于递归贝叶斯理论的状态估计步骤如下:

a)时间更新:

(3)

b)量测更新:

(4)

1.2 系统非线性约束

假设对于某个运动目标在k≥1的任意时刻,其状态矢量xk均满足如下非线性约束:

g(xk,k-1)=Bk

(5)

其中：g(·)与Bk∈x均为已知。那么在考虑系统约束的条件下将式(4)作为整个状态估计的目标函数:

J(xk)=p(xk|Zk),s.t.g(xk,k-1)=Bk

(6)

1.3 非高斯噪声模拟

假设ζ是具有非高斯密度函数的随机噪声过程,其可以被建模为两个统计独立的随机噪声过程之和:

ζ=α+β

(7)

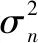
(8)

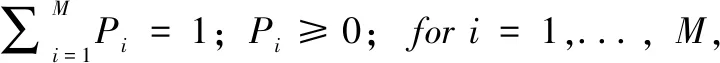
‖po-p*‖k=

(9)

2 带非线性约束的自适应高斯和卡尔曼滤波算法

2.1 自适应高斯和滤波策略

考虑如下离散系统:

xk+1=F(xk)+wk

(10)

zk=H(xk)+vk

(11)

其中：xk是状态向量,wk是具有非高斯统计特性的过程噪声,zk是测量向量,vk是具有非高斯统计特性的测量噪声,Φ和H是各自转移函数。由1.3节可知,假设wk=θk+αk,vk=λk+βk,那么wk和vk可分别表示为高斯和的形式:

(12)

(13)

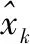
本文提出的带非线性约束的自适应高斯和卡尔曼滤波目标跟踪算法分为自适应高斯和滤波策略及非线性约束投影策略。而高斯和自适应滤波策略又主要分为两个部分：第一部分是分布式高斯和滤波;第二部分是权值自适应策略。约束投影策略将在2.2节介绍。

1)分布式高斯和滤波:

(14)

其中,Zk是当前时刻测量序列{z1,...,zk}。将两个偏差矢量θk和λk代入p(xk|Zk),引入贝叶斯规则,其可改写为:

(15)

代入式(14)可得:

(16)

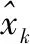
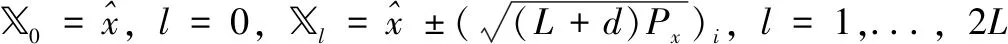
(1) 状态预测:

(17)

(18)

(19)

(2) 状态估计:

(20)

(21)

(22)

其中:

因此,式(16)改写为:

(23)

式(23)的协方差Pk满足公式：

(24)

2)权值自适应策略:

对于式(23)的加权项p(θk,λk|Zk)。引入Zk={z1,…,zk}序列及贝叶斯规则:

p(θi,λi|Zk)=

(25)

式(25)的分子第一项可以近似为高斯密度,表示为:

(26)

式(25)的分子第二项是给定过去测量序列Zk中θk=i,λk=j的预测概率值。可由下式得到:

(27)

(28)

(29)

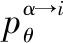
(30)

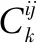
(31)

自适应高斯和滤波的本质是每个单独高斯项的估计乘以相应的权值。

2.2 状态约束投影策略

考虑引入目标约束先验知识。文献[14]通过引入拉格朗日乘子λ来求约束卡尔曼滤波的最优解。但此方法要求迭代的初始值λ0靠近λ的最优解。但实际条件下,好的初始值并不容易获得。这里考虑将非线性约束引入自适应高斯和滤波,进行投影量测更新,来获得更精确的估计。考虑2.1的自适应高斯和滤波,那么经过约束投影后的估计式表达为:

(32)

subjecttog(xk)-Bk=0

(33)

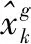
首先,重新选择k时刻的Sigma点,并进行非线性传播:

(34)

(35)

k时刻约束估计:

(36)

k时刻约束误差协方差及估计约束互协方差:

(37)

(38)

非线性约束卡尔曼增益:

(39)

计算k时刻的协方差及对权值自适应滤波器的输出进行约束投影修正:

(40)

(41)

3 系仿真实验

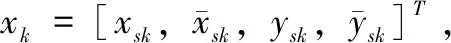
xk=Fxk-1+wk

(42)

yk=Hxk+vk

(43)

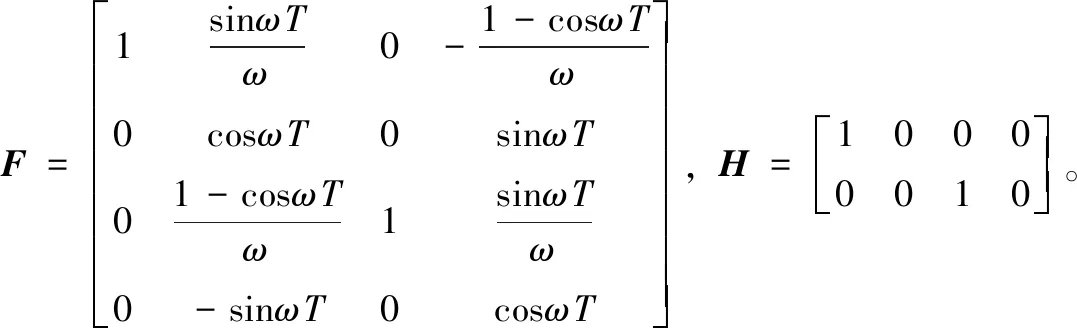
Rv=diag[25 25],P0=diag[49 1 49 1]

在目标初始位置处于真实位置条件下,图1给出了某一次蒙特卡洛仿真结果。图中分别显示了两个滤波器的输出,模拟的路段,以及小车真实位置和测量。真实位置用一系列绘制在路段上的(°)点表示。因为假设的小车具有恒定角速度,因此真实位置是等距分布在路段上的。将小车的运动轨迹看作约束并引入滤波器:

(44)

同时将文献[14]提出的一种非线性约束滤波器纳入比较。从图中滤波器的输出可以看出,由于约束信息的引入,文献[14]提出的算法能够跟踪小车的转弯运动。但是因为伽马噪声的影响,其跟踪精度大大降低,无法满足目前跟踪需求。因此传统约束卡尔曼滤波在非高斯噪声下难以达到令人满意的效果。而本文提出的自适应高斯和滤波与卡尔曼滤波结合后的滤波器输出基本都落在真实位置附近,性能明显优于文献[14]提出的滤波算法。

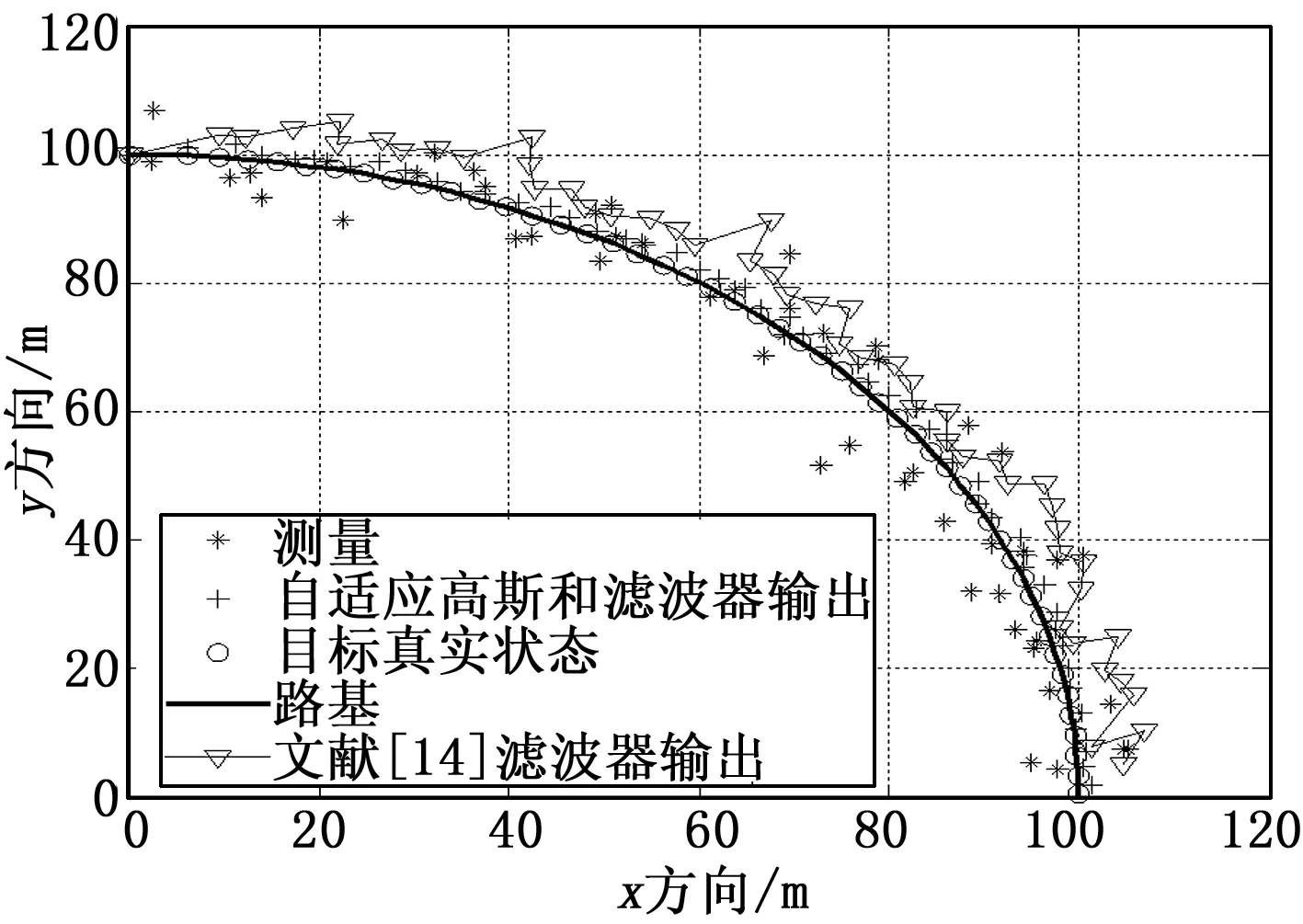
图1 情景1下各算法的目标跟踪结果

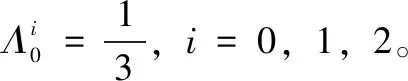
(45)

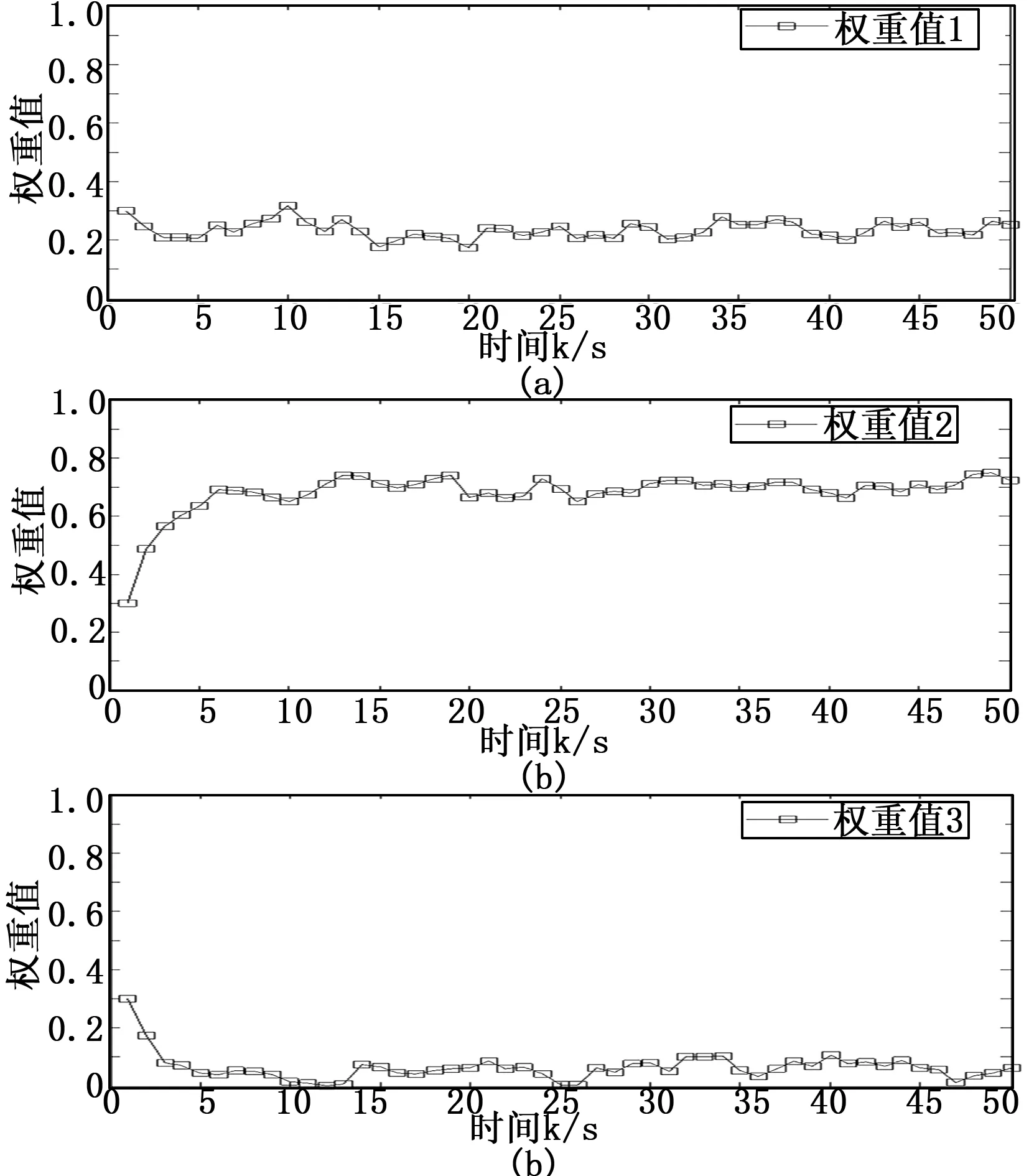
图2 θk的权重值

同时式(44)应满足以下两个条件:

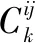
2)当某一个权重Λi≥1,令其等于1,同时令其它权重等于0。

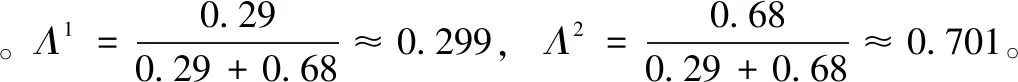
接下来在实验中考虑一种更加复杂的情景2,同时将PUKF和GSUKF两种算法纳入比较。采用500次蒙特卡洛仿真,以各算法的均方根误差作为目标跟踪精度的指标。计算方法如下:

(46)

为了验证算法在系统非线性条件下的性能,考虑加入更多传感器来实时跟踪小车的位置。假设有3个雷达站每个时刻k发送信号来获得3个距离,假设雷达位置分别为R1=(0 m,0 m),R2=(0 m,650 m),R3=(320 m,0 m)。由于R1处于原点,考虑在k时刻获得两个距离差,即每个时刻目标距R2与R3距R1的距离差si→1,i=2,3,则测量方程改写为:

yk=sk+vk

(47)

其中:sk=[si→1]i=2,3其它条件与情景1相同。3种算法的均方根误差如图所示。

由图3可以看出, 传统的高斯和卡尔曼滤波算法由于没有约束先验信息的导入,其收敛速度及精度都低于估计量投影法以及本文提出的算法。 因此,相对于传统的GSUKF,本文算法采用了高斯子项的权值自适应策略,并将系统非线性约束引入滤波器,从而能够得到更加准确的全局优化结果。 估计量投影法与本文算法类似,均能够在迭代初期快速收敛,但是由于无法消除伽马噪声的影响,其跟踪精度随着时间累积会大大降低。因此与估计量投影法相比,自适应高斯和卡尔曼滤波能加适合实际工程的使用。

情景3中将考虑更加实际的情况,即在初始时刻,目标的真实位置未知。量测噪声vk=βk(令λk=0)的协方差矩阵为R=diag([25 25])。算法首先使用2.1节的自适应高斯和滤波策略目标初始估计,来代入滤波器输出初值。初始协方差P0=diag([1027 1027])。其它情况与情景2实验条件相同,采用500次蒙特卡洛仿真实验,各算法的均方根误差如图4所示。

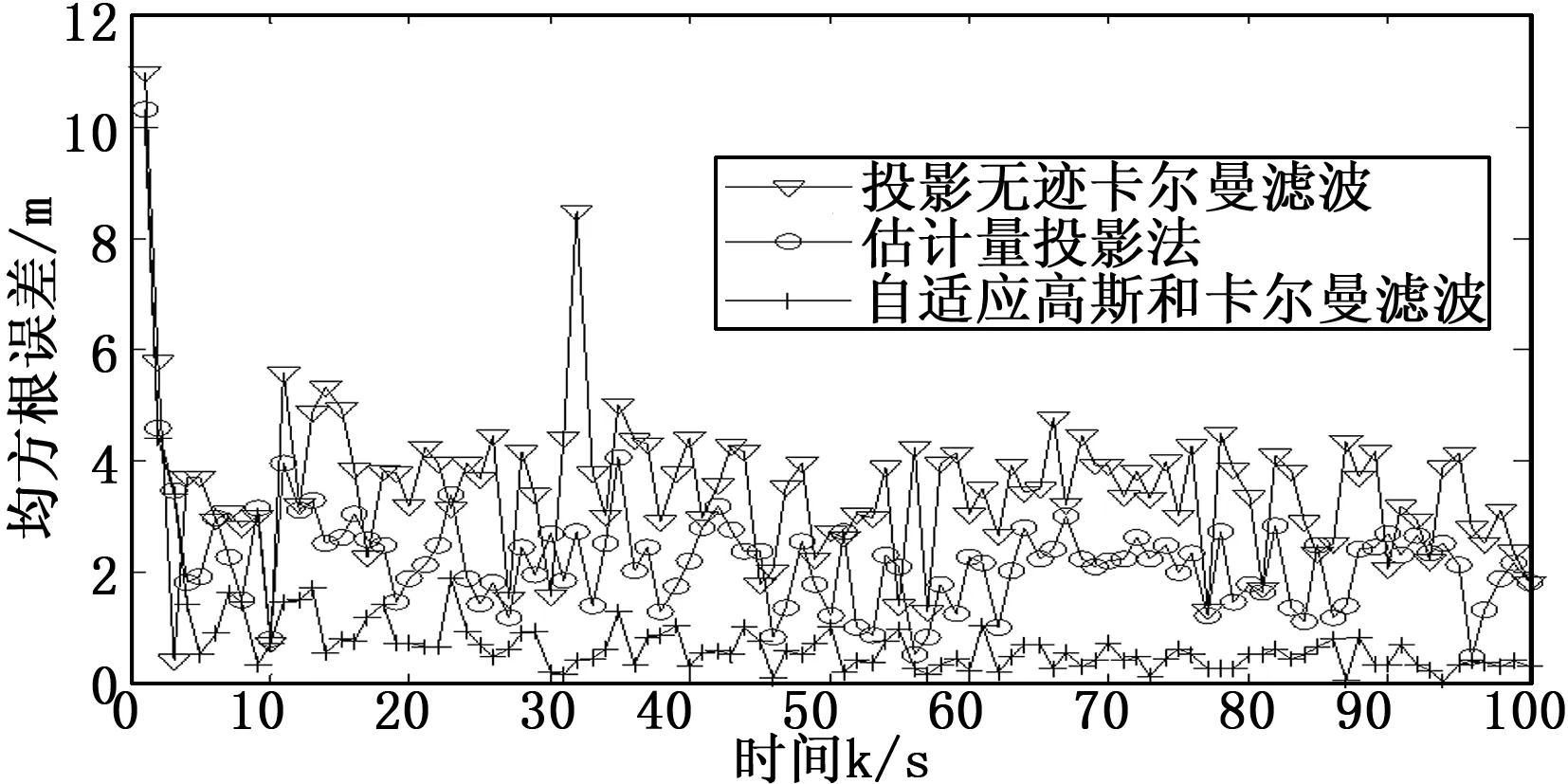
图4 情景3下各算法跟踪精度比较

由图4可以看出,由于各算法均引入约束信息先验,所以即使在初始状态非目标真值的情况下, 投影无迹卡尔曼滤波算法、估计量投影法以及本文提出的自适应高斯和卡尔曼滤波算法算法均能够快速收敛。但是与另外两种算法相比,本文算法的跟踪精度更高,说明非高斯噪声对另外两种滤波器产生了极大干扰。另外,对比图4和图3,当在量测方程引入非线性时,3种算法的误差曲线均会产生波动,使得所有误差曲线更加曲折。其中投影无迹卡尔曼滤波算法受到的影响最严重,表明其处理非线性问题能力较估计量投影法和本文算法更差。估计量投影法算法受非线性影响较小,但其累计跟踪误差会逐渐增大,对实际跟踪方案会产生较大影响。而本文算法在非线性条件下依然拥有较高的跟踪精度。因此,本文提出的算法在初始条件失真以及非线性非高斯条件下相对于目前约束卡尔曼滤波算法均具有更高的跟踪精度。

4 结束语

在本文中,针对无线传感网络中非高斯噪声下运动目标的跟踪精度问题,我们提出一种基于自适应高斯和的约束卡尔曼滤波目标跟踪算法。它首先计算目标状态的各初始高斯子项,然后对每个高斯项进行UKF滤波得到无约束条件下的状态估计,同时加入一种高斯子项权值自适应策略,解决了传统高斯和滤波算法的子项累积问题，提高了算法实时性。引入运动目标的非线性状态约束,将其看作一种无约束投影问题以获得全局最优解,提高了算法收敛速度与精度。最后通过仿真实验测试算法性能。仿真结果表明,相对于传统的约束卡尔曼滤波以及GSUKF等算法,本文提出的跟踪算法具有更高的跟踪精度。