黄河流域冲积层本构模型的深基坑适用性研究
王丹,王国富,2,路林海,曹正龙,徐前卫
(1.济南轨道交通集团有限公司,济南250101;2.山东科技大学 土木工程与建筑学院,山东 青岛 266590;3.同济大学 道路与交通工程教育部重点实验室,上海 200092)
随着中国经济的快速发展,地下空间开发的规模越来越大,而在繁华的城市环境里建设基坑往往面临着许多关键性的问题,例如,基坑设计深度较深、开挖面积较大[1]、相邻基坑紧挨错综复杂及与已有建筑物距离较近等,简单来说就是“深、大、紧、近”4个特点[2]。基坑的变形特性不仅与开挖方式及支护方案有着直接的关系,从本质上来讲与基坑所处的地层地质力学特征密切相关。黄河是中国的母亲河,沿线孕育出了许多繁华的城市,从地质力学特征上讲,沿黄河流域的地层形成规律具有高度的相似性,但由西向东也随着颗粒沉积的规律不同而缔造出地质力学特征差异较大的土层。
目前为止,许多学者利用不同的本构模型研究了黄河冲积典型区域中基坑开挖变形规律。例如代春泉等[3],利用二阶非线性牛顿体黏弹性塑模型研究了济南某深基坑开挖支护的变形规律;郑栋材等[4]以郑州某深基坑为工程背景,以摩尔库伦为本构模型分析了基坑支护方案的可行性,且模拟结果与实测数据比较接近;董建华等[5]对兰州某深基坑采用理想弹塑性本构模型对考虑地下水渗流的支护结构内力进行了分析,并且证明了联合支护体系是非常有效的。截止目前,对沿黄河流域的基坑本构模型适用性探究并不多,且学者之间没形成统一的观点。根据已有的研究成果,总结整理现有的本构模型并将一些不常用的本构模型应用到基坑变形分析中,探究黄河三大典型流域适用的本构模型,对指导工程施工、预测基坑结构变形具有重要的现实意义。
1 黄河流域地质力学特征分析
1.1 流域颗粒级配特征
在黄河厚冲积粘土地层形成的过程中(如图1所示),土体颗粒在连续运动的过程中受到冲击力(Px)、紊流上浮力(Py)、自重(G)及河床摩阻力(Fx)。每种力的表达方程为公式(1)~(4):

(1)

(2)
> 自重G=(γm-γω)·abd
(3)
> 摩阻力Fx=f·(G-Py)
(4)
式中:λx、λy为冲击力系数即上浮力系数;ρ为水的密度;γm为土粒重度;γω单位体积水重度;f为土粒与河床的阻力系数;a为土颗粒高度;b为土颗粒厚度;d为土颗粒宽度。

图1 土颗粒受力示意图Fig.1 Schematic diagram of soil
颗粒若跟随水流运动,则受力方程应满足
Fx≤f·(G-Py)
(5)
得出颗粒的流动速度为
(6)
可见,颗粒的流动速度与粒径的平方根成正比,并且根据水力学知识得到砂砾自重与启动流速的关系为:G=Cν6,即颗粒流速与粒径成非线性高次方比例,所以,在流速较大的区域,对大粒径的砂砾具有较好的搬运能力,造成黄河流域由西往东颗粒级配逐渐变好,使得地层在压缩时能达到较高的密实度和较差的渗透效果,地层抗剪强度及其他力学指标得到相应提升。
1.2 地域地层分布特征
土颗粒在流动中主要依靠自身重力沉淀,且沉降速度与自身体积有密切关系。由流体力学知,颗粒在匀速流动条件下的沉降速率为
(7)
根据著名的水槽试验,在流水运动中土体颗粒的沉淀规律与颗粒的质量、水速密切相关,其中,石英土体颗粒的粒径与流速存在如图2的关系。由图2可知,对于固结的粘土和粉砂体,随着粒径的逐渐增大,流速呈先降低后升高的规律,当细砂的粒径为0.08 mm时,颗粒流速最低,因此,在深处地层中以0.08 mm粒径的细砂为主。对于未固结的粘土和粉砂,当粒径较小时,颗粒之间的附着力大于流水冲刷力,使得颗粒容易发生沉积。因此,在黄河流域西部水流较大的区域,如宁夏、兰州等地,深层以未固结的粘土和细砂为主;在黄河流域东部,如郑州、济南等地,深部地层主要以细砂为主。以上特征塑造了黄河流域不同地区各自的力学特征,在具体工程中以地层扰动后的应力-应变响应规律表现出来。

图2 黄河土体颗粒冲积关系图Fig.2 Relationship of soil partical in alluvial
1.3 兰州厚冲积地层力学特征
为直观了解兰州市黄河厚冲积地层力学参数分布规律,选取兰州多处区域为代表样本,绘制出厚冲积黏性土层的地质数据表[6]。由图3可以看出,兰州厚卵石分层简单,10 m以下皆为卵石层,且深度达上百米,随着深度的增加,卵石层有胶结现象。填土重度在20 kN/m3,而卵石层重度多在21~22 kN/m3之间,且随深度有所增加;中砂及上层卵石层的含水率较低,未超过10%,主要是透水性较好,同时其饱和度也较低,约在70%~85%之间;变形模量随深度有明显增大的趋势,深处的卵石层可通过计算作为持力层;由于卵石层取样困难,其地勘报告中直剪结果粘聚力给出一个常用值10 kPa,但同时,在原位进行了大型直剪试验,设计中可以参考剪切曲线选取粘聚力;而内摩擦角随深度增加;静止土压力在小于10 m的填土及砂层中接近0.5,但是随深度增加,逐渐减小到0.2,渗透系数在中砂层及上部卵石层中较大,因下部卵石层有胶结现场,加之颗粒级配优于上部卵石层,因此,深部卵石层渗透系数有减小的趋势。
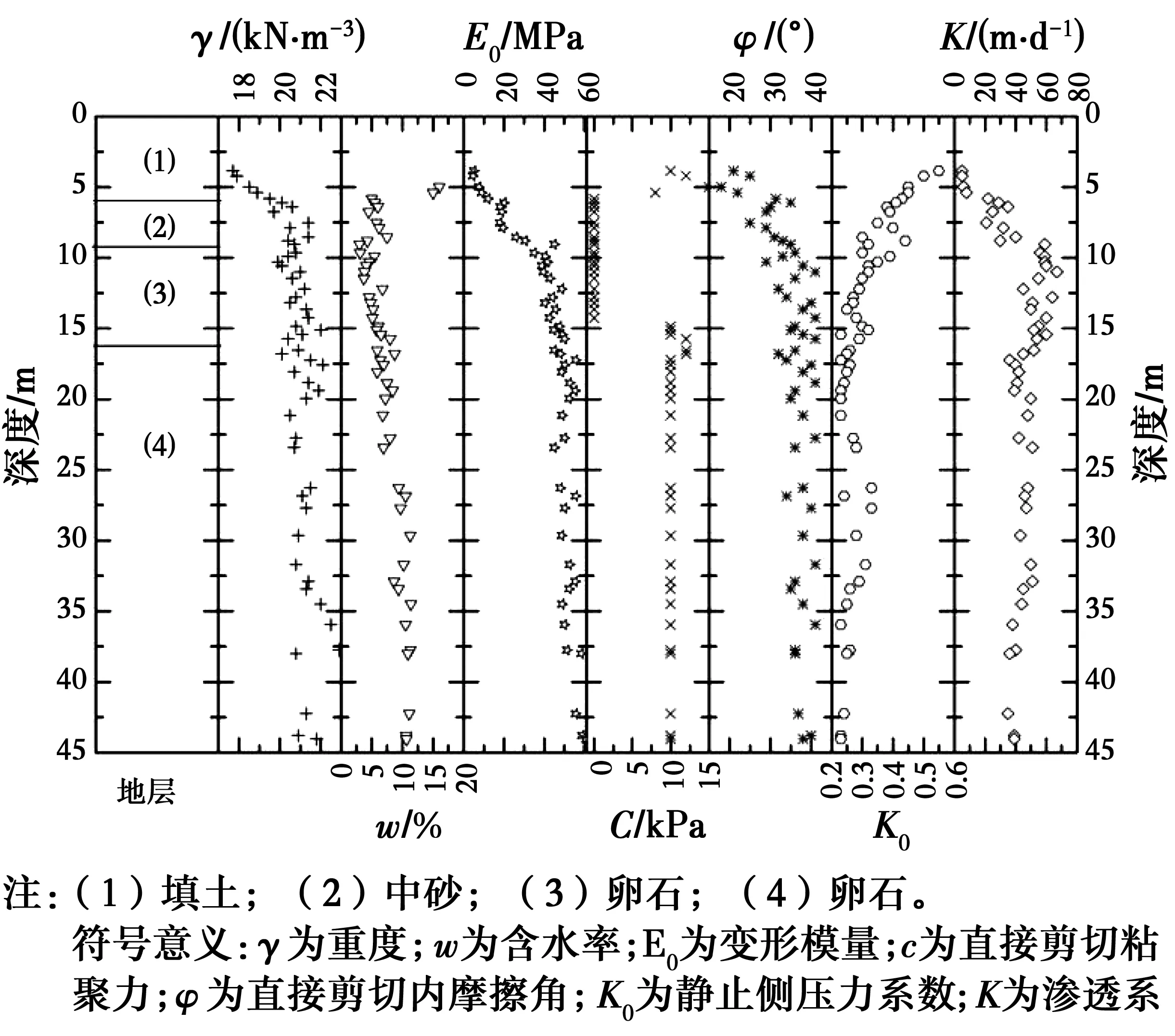
图3 兰州厚卵石层地质力学参数特征Fig.3 Characteristic of stratum of thick alluvial in
1.4 郑州厚冲积地层力学特征
郑州多为黄河冲积的粉土、粉质砂土、砂质粉土及粉质粘土,根据郑州地质勘察报告,以及郑东新区的地下建筑工程勘察报告,统计了几种常规地质参数[7],如图4所示。
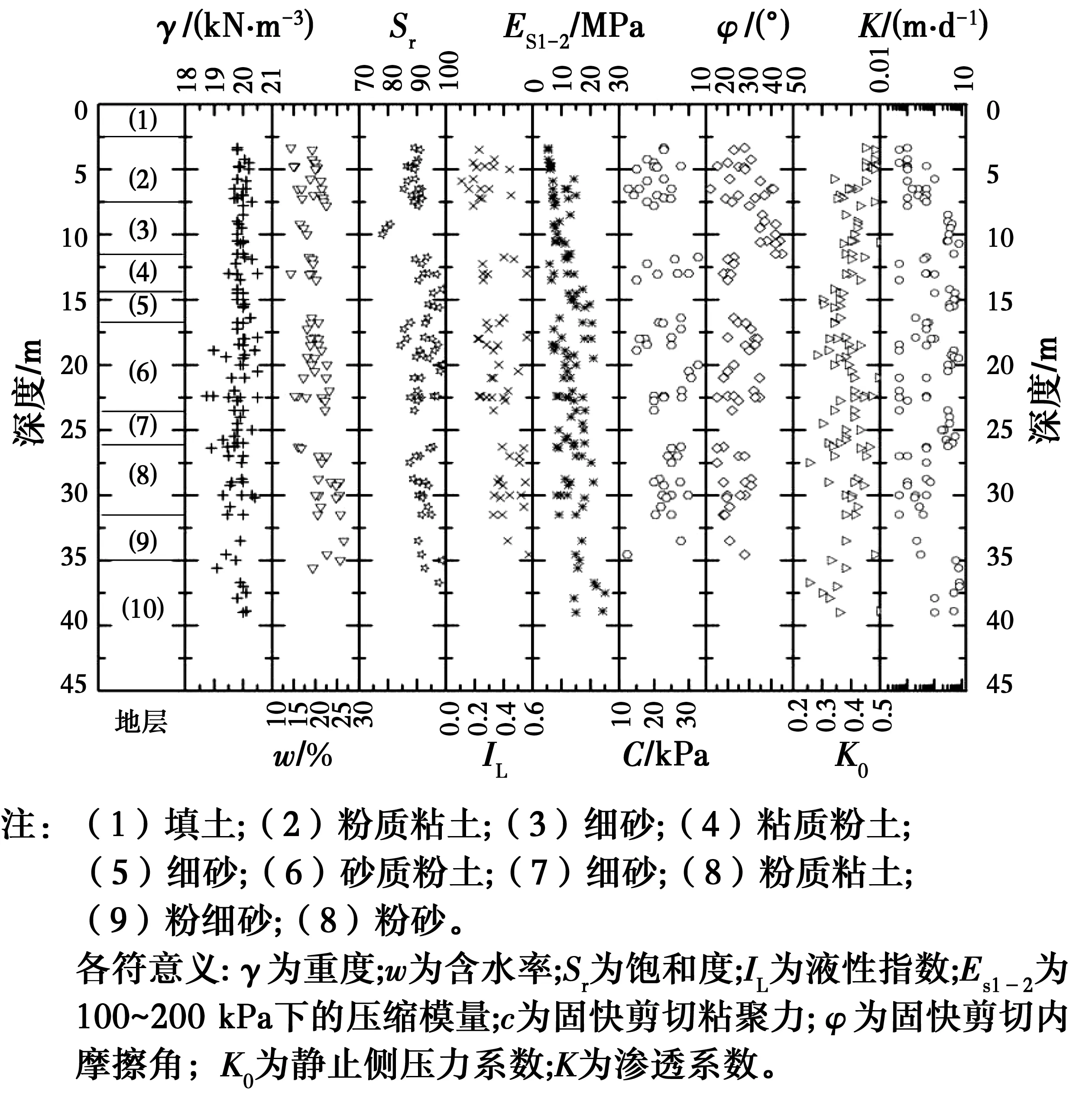
图4 郑州厚粉砂层地勘参数Fig.4 Characteristic of stratum of thick alluvial in
由图4中数据可以看出,郑州的土层参数较均匀,多为粉质粘土、粘质粉土或细砂等易产生液化的土层,重度随深度较均匀;含水率及饱和度在砂层中未测试,因此,图中数据间断,但测试得到的饱和度较高,超过80%;液性指数在0.2~0.6之间,处于硬塑或可塑状态,由于下部含水率较高,导致下部土体液性指数稍高;土体的压缩模量随深度增加,但多在15~25 MPa之间,作为持力层需要进行加固;固结快剪实验得到的参数与常见粉土性质相似,出于保守估计,粉砂或细砂给出的粘聚力为零;由于粉质粘土与砂层的渗透系数差距较大,故利用对数坐标统计,基本上粉质粘土及粘质粉土有黏粒的存在,渗透系数<0.5×10-6m/s,而粉砂或细砂的渗透系数>2.0×10-4m/s。
1.5 济南厚冲积地层力学特征

图5 济南厚冲积地层力学参数特征Fig.5 Characteristic of stratum of thick alluvial in
通过搜集济南市多处黄河厚冲积地层力学特征,选取济聊城际济南至长清段区域基坑为代表样本,绘制了厚冲积黏性土层的地质参数[8]统计图,如图5所示。由图5可以看出,济南厚冲积平原地区的土层参数较均匀,多为粉质粘土、黏土为主,土层重度随深度增加,下部土层较密实;因在粘性土中渗透系数较小,含水率分布较为均匀;测试得到的饱和度从70%随深度逐渐增加至90%,上部土体按照饱和土计算得到的结果存在一定误差;液性指数在0.2~0.8之间,处于硬塑或可塑状态,由于下部含水率较高,导致中间部分土层液性指数较高,处于可塑状态,其承载力相对较低;土层标贯击数随深度也有一定的增加,与液性指数相对应;土体的压缩模量分别采用100~200 kPa及200~400 kPa两个级别,随深度增加,压缩模量有增大的趋势,但变化幅度不大,多在15~25 MPa之间,作为持力层可能需要加固处理;固结快剪实验得到的粘性土的粘聚力随深度增加,但内摩擦角规律不明显;静止侧压力系数表明上层土体的以竖向应力为主,水平向应力较小,随着深度的增加,水平向应力逐渐增加,静止侧压力系数集中在0.4附近。
2 岩土本构模型甄选
土体是具有极为复杂力学行为的天然材料,在其变形的过程中会包含弹性变形、非线性弹性变形、塑性变形、蠕变变形及应力松弛等阶段[9-11]。不同的区域土体变形具有显著的差异,且均具有各自的特点。在基坑开挖支护过程中,土体单元会反复经历加载-卸载过程,单元处于复杂应力状态,因此,不同的屈服准则判断出的土体状态截然不同。经过甄选分析,最终选取选取5种本构模型:摩尔库伦模、邓肯E-ν模型、修正剑桥模型、德鲁克-普拉格模型及简尼模型对黄河流域地层本构模型基坑开挖适宜性进行分析。
2.1 摩尔库伦模型
摩尔库伦模型是以M-C屈服准则为判断基础的线性本构方程,当土体微单元的剪切应力与正应力之比达到某一极限值时便出现屈服。该模型材料参数少,可将复杂的应力路径进行线性简化。基坑开挖过程中,坑底土体单元是卸载过程,但坑壁单元由三向受力状态变为双向应力状态,等效于加载过程,因此,基坑施工对土体单元的自稳状态扰动也较为剧烈。
M-C屈服准则在发生破坏时,土体单元将沿某一斜截面发生剪切屈服破坏。如图6所示,在主应力区域(σ1-σ3)内,M-C屈服线将第二象限分成了两部分,在σ3较大的正向区域内是破坏区域,在靠近左边原点的区域是稳定区域。其中,屈服线的斜线方程表达式为

图6 M-C屈服轨迹线
(8)
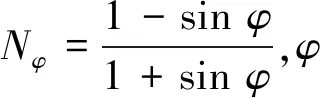
2.2 邓肯-张本构模型
邓肯E-ν模型(如图7所示)是以广义胡可定律为基础的非线性弹性模型,且模型中的参数形式简单,可准确追踪岩土体的弹性变形及塑性变形。邓肯-张模型定义最大与最小主应力之差(σ1-σ3)与轴向应变εz呈双曲线关系,并且轴向应变εz与体积应变εv也同时呈双曲线关系。

图7 邓肯-张本构模型应力应关系Fig.7 Relationship of stress and stain of
在邓肯-张模型中的E-ν模型,其切线模量Et及体积变形模量Kt的表达关系式分别为:
(9)
(10)
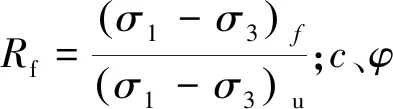
2.3 修正剑桥模型
修正剑桥模型(Modified Cam-clay Model)(如图8所示)在追踪有一定适应流动性材料变形时具有较高的准确性,并且在材料单元体积发生变化时,其抗剪强度也会做出相应调整。根据相关资料[12],正常固结饱和粘性土的孔隙比e和单元的应力p、q可以用p-q-e三维坐标中的“状态边界面”(图中ACEF)进行描述;正常固结饱和砂性土,在破坏时会出现体积收缩的现象,其稳定状态是在初始三向等固结线VICL和临界状态线CSL之间的“状态边界面”,因此,修正剑桥模型可描述正常固结的粘性土和砂性土的破坏特征。

图8 修正剑桥模型Fig.8 Modified cambridge
在土体单元出现塑性破坏时,有
(11)

根据正交原理对硬化参数A*进行整理,并对式(11)进行微分代换处理,得到应力应变本构方程为
{dσ}=[Dep]{dε}
(12)
(13)
2.4 德鲁克-普拉格模型
摩尔库伦模型如图9所示可根据应力张量第一不变量I1和偏应力第二不变量J2及Lode夹角θσ描述土体单元在塑性破坏时的应力关系。鉴于M-C屈服面在偏平面上为规则多边形,在有限差分法计算时模型不易收敛,因此,对拐点进行圆弧处理,得到D-P的屈服面表达方程为
(14)
式中:α为与内摩擦角有关的常数;I1为第一应力不变量;J2为第二偏应力不变量;K为与内粘聚力有关的常数。
德鲁克-普拉格准则(如图9所示)的屈服界限与土体的破坏变化无关,不存在强化准则,并且在数值模拟中需要输入土体的剪胀角ψ。当剪胀角ψ小于内摩擦角φ时,D-P屈服准则可描述低摩擦角的软粘土塑性破坏特点;当剪胀角ψ与内摩擦角φ相等时,D-P屈服准则可描述正常固结粘性土塑性破坏特点。

图9 D-P屈服轨迹
2.5 简尼模型
简尼模型(如图10所示)是由Hooke体与M体并联得到的M/H体。粘性土在卸载时并不会出现简单的弹性变形,会附带一部分蠕变变形,两者相互叠加与折减。当材料受到较大作用力时,牛顿体退化为刚体,该模型等同于两个Hooke体并联;当材料所受的作用力较小时,牛顿体会吸收一部分力对并联弹簧的变形进行缓冲。因此,提出M/H体可较准确地对厚冲积粘土地层基坑卸荷时出现的非稳定蠕变变形进行描述。

图10 简尼本构模型Fig.10 Constitutive mdoel of
K体的本构方程
σk=E1εk
(15)
M体的本构方程为
(16)
由并联模型后的应力-应变关系知
σ=σk=σM
(17)
ε=εk+εM
(18)
对式(17)两边求一次导得
(19)
对K体的本构方程两边求导,联立式(17)得
(20)
将式(20)和式(16)带入式(19)得简尼本构方程
(21)
设简尼体受到的总应力为σ=σ0=const,由简尼体初始(t=0)加载时的M体的蠕变方程及K体蠕变方程联立得
(22)
2.6 本构模型的验证
利用自带德鲁克-普拉格、摩尔库伦及修正剑桥本构模型的有限差分法计算软件FLAC3D,并通过C++语言对计算软件进行二次开发,将前文的简尼本构模型及邓肯-张模型进行程序化。在兰州、郑州及济南三地甄选出长度及宽度相似且支护方法相同的3个基坑,经搜集基坑资料,遴选出兰州轨道交通1号线某试验深基坑、郑州某商业基坑及济南西客站某深基坑。
2.6.1 模型建立 根据基坑尺寸建立一个长×宽×高=100 m×40 m×60 m的共同模型,并可依照基坑设计尺寸调整模型开挖范围。模型四周为水平链杆约束,底部为固定约束,顶部施加20 kPa的施工荷载。模型三维视图如图11(a)所示,基坑支护结构示意图如图11(b)所示。

图11 基坑数值模型Fig.11 Numerical model of
2.6.2 参数选取 摩尔库伦的模型中c、φ初始值可根据地质勘察资料得到,将c、φ与某一折减系数逐次迭代,结合现场单桩堆载实验,以0.98的逼近率反复调整模型参数,实现对地层参数的反演优化确定;邓肯-张模型的初始参数(K、n、Rf、C、φ、D)按照文献[12]的数值试验模型方法,在该文献的基础上,将兰州、郑州、济南三地的地层地勘参数,按照文献的基础参数(C、φ值)进行插值,按等比例确定K、n、Rf值,然后再以三地基坑的围护桩变形调整各自的参数,同样以0.98的逼近率进行参数验收;修正剑桥、德鲁克-普拉格及简尼模型中的牛顿体、弹簧体的参数采用同样的方法分别参考文献[13]、文献[14]、文献[15]进行确定。各模型参数选取时,内粘聚力、内摩擦角及弹性模量等共同参数均采用统一数值,限于篇幅,现只罗列出济南地区非岩层中关于五种本构模型的参数选取值,如表1所示。
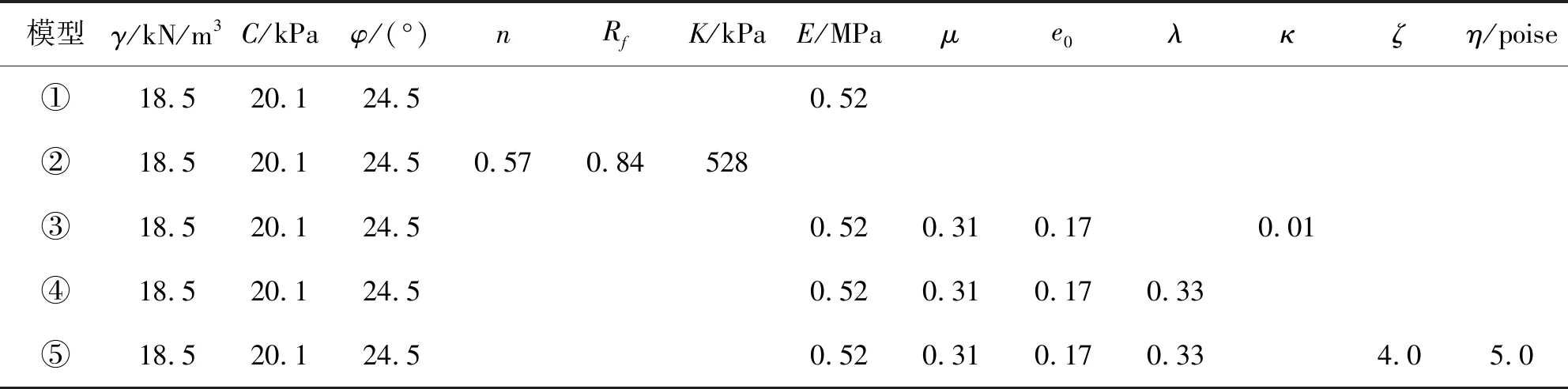
表1 济南地区各模型参数反演值Table 1 Suitable parameters of different model in Jinan
注:①为摩尔库伦模型,②为邓肯-张模型,③为修正剑桥模型,④为德鲁克-普拉格模型,⑤为简尼模型;γ为重度,C为内粘聚力,φ为内摩擦角,n为无因次指数,Rf为破坏比,K为初始体积变形模量,E为弹性模量,μ为泊松比,e0为初始孔隙比,λ为侧压力系数,ζ为流变指数,η黏性系数。
2.6.3 模拟过程简述 Flac3D对岩土体的数值解是建立在满足基本方程(平衡方程、几何方程、本构方程)和边界条件,不同本构模型得到的数值有所差异,但各本构模型的模拟过程相同,大体分为以下4步:
1)确定有限差分网格、本构模型、材料参数、边界条件。网格一般采用六面体形式,边界条件和初始条件定义模型的初始状态,本模拟网格采用六面体,初始条件已在上文介绍。
2)输入本构模型参数,运行至最大不平衡力为零,根据实测数据反演调整初始参数。在模型参数输入完成之后,根据单桩堆载实验(模型中单独设置)逐步调整初始参数,但模拟监测数据与实测数据之比在0.98~1.0之间时,停止参数反演。
3)基坑分步开挖。通过软件中内置的空模型(开挖模型null)实现,并同时设置结构单元(横撑Beam单元、锚索Cable单元、初期支护Liner单元),并将模型运行至最大不平衡力为零。
4)汲取模拟监测数值,并进行分析。在模拟全过程中,监测点实时监控数值变化规律,将监测结果导出、对比,完成数据分析。
3 各本构模型结果及适用性分析
3.1 兰州流域基坑本构模型适用性分析
从理论上讲,基坑开挖中土体本构模型最好能同时反映土体在小应变时的非线性行为和土体的塑性性质,因为反映土体在小应变时的非线性行为的本构模型能给出基坑在开挖过程中更为合理的变形,包括支护结构的变形和土体的变形,而反映土体塑性性质的本构模型对于正确模拟主动和被动压力具有重要的意义。基坑地表变形、侧土压力可直接表征基坑受力状态,反映土体应力-应变规律;锚索轴力是支护结构与地层间的结合力,可反映土体的剪胀性及流变性或其结构性,进一步反映出土体本构模型的特性。
3.1.1 基坑锚索轴力模拟结果分析 以锚索为例,锚固段依赖灌浆材料及周边围岩的相互作用传递外荷载,土体材料的性质影响结构与围岩之间应力传递路径及应变消减形式,所以土体单元的应力应变关系可直接决定锚束体的极限抗拔承载力。因此,针对兰州地区厚冲积层本构模型的适用性研究,选取了可表征地层蠕变特性的锚索轴力进行对比分析。
修正剑桥模型监测得到的数据分布(如图12所示)规律与监测数据的规律比较相似,在基坑施完成8个月时,修正剑桥拟合的锚索轴力开始下降。在这个过程中,坑壁土体向基坑内部移动,地下水位恢复到正常位置,土体单元在竖向浮力及侧向释放效果的作用下,体积出现膨胀。根据修正剑桥的力学特征可知,该模型修正了剑桥模型的弹头形屈服面,并采用帽子屈服面,借助粘弹性体的应变硬化参数实现了材料体积发生改变时,抗剪强度出现相应调整。这种特征可以准确追踪黏性土在出现非线性或依赖于水平约束力的应变变化特征,对兰州地区基坑锚索轴力的预测起到良好效果。
在简尼模型下,锚索轴力随着时间的延伸呈现出快速下降的趋势,在时间达到25个月时,轴力达到稳定状态。简尼模型中牛顿体具有较强的时间特性,在外力施加的短时间内牛顿体不产生变形,在受力保持阶段,牛顿体的抗滑能力迅速下降。土体单元发生位移错动,土体之间及土体与锚索之间的粘结力下降,杆体出现滑动,造成轴力损失严重;摩尔库伦模型在基坑土体未发生破坏之前,认定材料的应力应变关系服从胡克定律,对于强度较好的材料具有较高的准确性,但是该模型与时间因素无关,不能追踪土体在发生蠕变过程中的应力-应变特征;邓肯-张本构模型不与时间相关,在基坑稳定阶段的轴力不发生变化,其屈服准则不能反映出土体蠕变特性,鉴于黄河厚冲积粘土地层土体在变形时会伴有剪胀特性,在基坑侧壁出现水平位移时,相邻土体单元的咬合力会增大,因此,在土体剪胀角ψ小于内摩擦角φ时,土体在未达到破坏时握裹在锚索上的轴力是增加的,所以,邓肯-张本构模型不能真实反映软粘土基坑锚索轴力的变化规律。
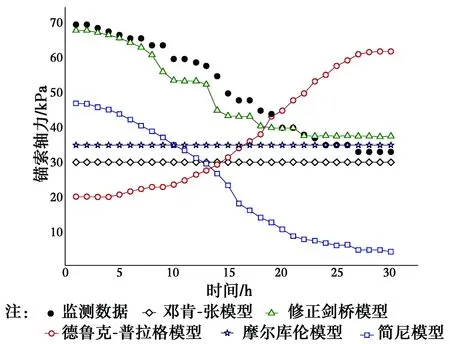
图12 兰州基坑锚索轴力变化规律Fig.12 Axis force of anchor in
3.1.2 基坑侧压力数值分析 图13为基坑开挖完成之后的主动土压力及被动土压力模拟及监测数据对比图。可知:1)修正剑桥模型与实测值最为吻合,变形规律相似,在基坑主动土压力区随着基坑深度的增加压力逐渐增大;在基坑底部被动土压力区,侧土压力方向发生改变,并且也随着深度的增加而增大。2)简尼模型模拟结果在主动区随着深度的增加,压力增加速度逐渐放慢,与实测值相差较大。3)邓肯-张模型和德鲁克-普拉格模型得到的模拟数据随深度的增加,变化比较曲折,在基坑坑底位置主动土压力最大,但坑底以下,主动土压力开始减少,与实测不符。4)摩尔库伦模型土压力曲线趋势整体上与实测曲线较为相同,但具体数值差别较大,特别是在基坑底位置,曲线拐点值较小。
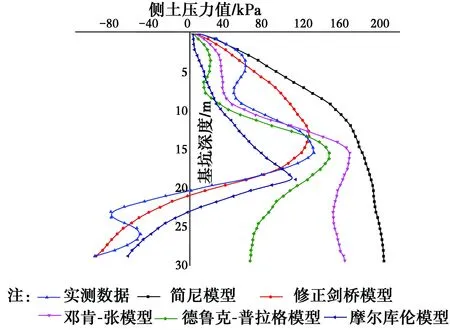
图13 兰州基坑侧土压力变化规律Fig.13 Soil force of foundation in
3.1.3 基坑围护结构变形模拟分析 图14为各模型下基坑围护结构水平位移变化曲线,5种模拟曲线与实测数据各自特征较明显,可看出:①修正剑桥模型在整体规律上与实测数据较为吻合,实测数据在深度10 m位置出现拐点,但大体趋势是在14 m位置处出现最大水平位移,数值为12.0 mm,修正剑桥模型模拟最大值为10.2 mm。②简尼模型及邓肯-张模型得到的数据偏大,最大值分别为16.0 mm和13.0 mm,且最大值出现的位置与实测值相差较大。③德鲁克-普拉格模型及摩尔库伦模型模拟的数据偏小,最大值分别为5.8 mm和3.1 mm,且最大值出现的位置与实测值偏差也较大。

图14 兰州基坑围护桩变形规律Fig.14 Horizontal displacement of pie in

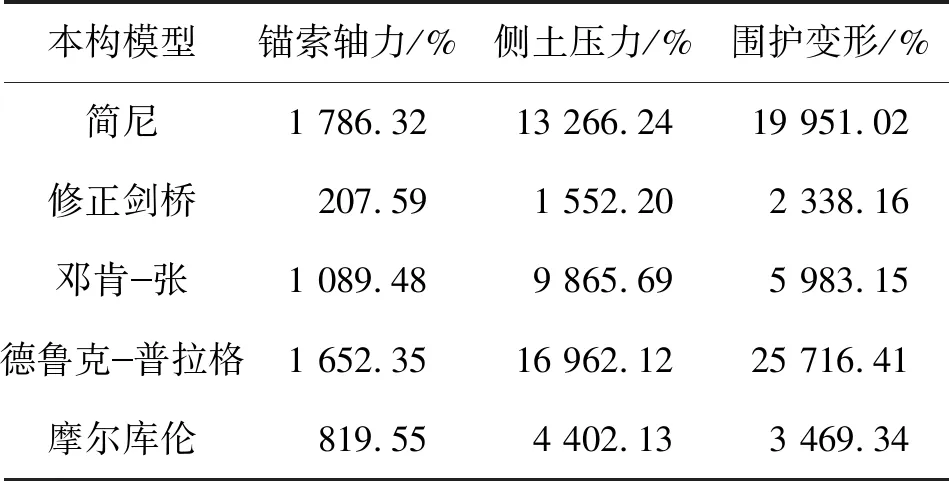
表2 兰州地区各本构模型模拟误差和值表Table 2 Suitable parameters of different model in Lanzhou
3.2 郑州流域基坑变形规律本构模型分析
3.2.1 基坑土压力分布规律分析 根据理论及经验可知,土压力与地层的性质有直接的关系,而在设计时,土层的性质与土体的本构模型是直接相关的。因此,基坑变形规律可透过土压力分布特征进行剖析,换个角度,地层的本构模型是表征基坑变形衍化的着手点。
图15为基坑开挖支护完成后的主动与被动土压力分布规律,在基坑近土侧,主动土压力值随不同的本构模型具有较大的差别,并且在基坑不同的深度处主动土压力值与被动土压力值出现明显分歧。在主动土压力的一侧,摩尔库伦屈服准则对土体加载-卸载均采用同一个弹性模量,由摩尔库伦破坏包络线推算在基坑侧壁土体状态改变时,模型中的最大主应力状态对材料的屈服情况起决定作用。基坑土体移出或者变位时,摩尔库伦模型模拟得到的主动土压力值与实际监测得到的土压力值最为接近,而且变化规律也高度相似,两者的数值大小随基坑深度的增加呈现快速增加后开始降低。

图15 郑州基坑土压力分布规律Fig.15 Earth pressure law of pit in
简尼模型模拟得到的土压力值随着基坑的深度呈台阶状分布,即跳跃式分布,比实际监测值偏大,简尼模型中牛顿体的应变对应力十分敏感,在基坑不同深度处土体单元三向应力状态中的主应力差别较大,变化的应力差造成简尼模型对侧压力识别能力的波动,导致如图15中曲线的规律;在基坑开挖底面附近,土体进入塑性状态,德鲁克-普拉格屈服准则与摩尔库伦屈服准则相似,但其考虑了平均主应力对土体抗剪强度的影响而发展的一种准则,在坑底土体回弹过程中,中间主应力逐渐向第三主应力靠拢,致使该模型模拟得到的土压力模型由零开始迅速增大,侧压力值在距离坑底9 m左右达到最大,随后出现下降;邓肯-张模型拟合得到的被动土压力分布规律与德鲁克-普拉格结果规律相似,但最大被动土压力值的位置出现了下移,该模型不能识别材料的剪胀特性,在基坑浅部土体发生隆起或者体积膨胀时,单元之间的相互作用力无明显改变;对于修正剑桥模型得出的被动土压力分布规律与邓肯-张及德鲁克-普拉格模型拟合的结果截然不同,在距离坑底表面一定距离处,主动土压力均为零,在深度达到6 m时,被动土压力逐渐开始增加,并且数值与深度呈指数关系,该模型证实了在受扰动的基坑底部土体是塑性发展的。
3.2.1 本构模型适用性分析 通过总结表3中对本构模型适用性的分析,可知:摩尔库伦模拟的锚索轴力、侧土压力及围护结构变形误差分别为102.21%、42.71%和132.11%,较其他模型的误差值最小,可初步判断摩尔库伦模型对最终基坑开挖过程中的结构及土体变形而言具有较高的准确性。

表3 郑州地区各本构模型模拟误差和值表Table 3 Suitable parameters of differentmodel in Zhengzhou
3.3 济南流域基坑变形规律本构模型分析
3.3.1 基坑围护结构变形规律分析 基坑开挖在根本上来讲是土体单元加载-卸载的过程,地层的变形特征可通过围护结构的位移规律及地表隆起与塌陷进行表征,且不同本构模型下的地层变化规律差异性也较大。因此,针对济南基坑施工全过程中,各本构模型下的围护桩及地表土体变化规律如图16所示。
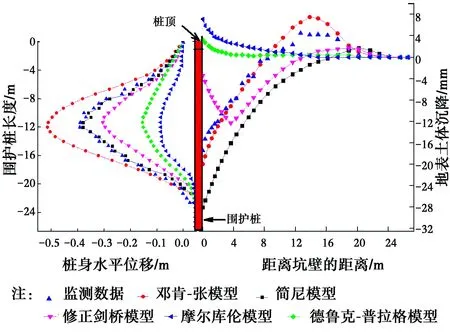
图16 济南基坑变形规律Fig.16 Deformation law of pit in
通过数值模拟分析可知,在描述围护桩水平位移时,5种本构模型得出的数据在总体规律上近似,均在距离桩顶12 m位置处出现最大水平位移。模拟计算结果最为保守的是德鲁克-普拉格本构模型及摩尔库伦模型,德鲁克-普拉格模型计算的桩体最大水平位移仅为4.5 mm,因为德鲁克-普拉格模型考虑了第二主应力的作用,使得土体单元处于更为稳定的状态,致使基坑侧壁土压力值较小;摩尔库伦模型会放大土体单元的抗拉能力,使土体材料不易破坏;模拟计算结果最为危险的是邓肯-张模型,模拟得到的围护桩最大水平位移比实测数据多出5.1 mm,因为邓肯-张模型的抗剪强度参数可以随着土体单元体积的变化而自我调整,在基坑开挖卸荷时,土体单元体积出现扩增,导致其抗剪强度参数降低,使得侧土压力计算偏大;与实际监测数据最为接近的是简尼模型,简尼模型考虑了土体蠕变过程,并且M体与K体通过并联模拟了土体的非线性变形规律,在土体卸荷的瞬间,K体的瞬时变形由于M体中的牛顿体而得到抑制。在基坑开挖完成后的一段时间内,土压力稳定之后,简尼模型仍然具有变形能力,与基坑长期变形规律较为吻合,因此,该模型下计算值与实测值较为接近。
5种本构模型下,地表土体变形大体呈现3种规律。其中德鲁克-普拉格与摩尔库伦模型下,改进了结构背部土体变形状态,表现出邻近基坑侧壁土体隆起,与现场施工经验完全不符,因为这两种模型均为弹塑性模型,在基坑卸荷时,土体单元出现的应力释放致使围护桩回弹,并带动周边土体上移;邓肯-张模型能自动调整自身抗剪强度及弹性模量,从而准确反映基坑卸荷及加载下的土体体积变化,在此模型下,靠近围护桩位置的土体下沉量出现“粘滞性”,整条曲线呈现“汤匙”型,与现场实测数据规律较吻合,桩后土体下沉的“粘滞性”是由于围护桩的轻微回弹导致土体上抬。
3.3.2 本构模型适用性分析 根据前述分析判断方法,整理如表4的各模型误差统计表。可以看出,在描述地表变形规律方面,邓肯-张模型较其他模型具有高准确度,同时,在侧土压力及围护结构水平位移方面,简尼模型得到的曲线与实测数据误差为62.25%。由此初步判断,在基坑围护结构变形方面,简尼模型具有较高的准确度。

表4 济南地区各本构模型模拟误差和值表Table 4 Suitable parameters of different model in Jinan
4 结论
以黄河典型的厚冲积地层—兰州、郑州、济南三地的代表基坑为工程背景,结合冲积地层的地域地层力学特征并分析五种本构模型各自的屈服特征及适用条件,研究了三大区域中基坑适用的本构模型。
1)沿黄河流域由西往东颗粒级配逐渐提高,地质力学特征差异较大。对于未固结的粒径较小的粘土和粉砂,在河流搬运时易发生沉积,导致西部水流较大的区域深层以未固结的粘土和细砂为主。
2)简尼模型能较准确模拟济南基坑围护桩的水平变形规律,并且M体与K体的并联体现了土体的非线性变形规律;邓肯-张模型通过自身参数的调整可准确反映基坑卸荷及加载下的土体体积变化,从而追踪济南基坑地表土体沉降规律。
3)摩尔库伦模型可较准确模拟郑州基坑开挖完成后的墙后主动土压力分布规律,该模型下主动土压力随着基坑深度的增加呈现快速增加-缓慢增加-快速增加3个阶段;在坑底被动土压力区域,德鲁克-普拉格与邓肯-张模型拟合的土压力规律相似。
4)修正剑桥模型的抗剪强度可根据土体单元的体积变化做出调整,可较好地模拟兰州基坑锚索轴力随时间变化的规律;简尼模型因牛顿体较强的时间性特点,拟合得到的锚索轴力变化曲线具有明显的蠕变特性。

