“建模—析模—用模”策略在生物学教学中的运用

蒋 进 李 椿

(江苏省泰兴中学 泰兴 225400)

普通高中生物学课程标准(2017年版)将模型纳入基础知识范畴，并将模型方法规定为高中学生必须掌握的科学方法之一[1]。本节课“种群数量的变化”教学采用“建模—析模—用模”的教学策略，引导学生运用所学知识分析并解决实际问题。

1 教材分析

“种群数量的变化”一节是人教版高中生物学教材(必修3)第4章第2节的内容。本节内容安排在种群的特征之后，学生已有相关知识作铺垫。在自然界中，某种生物种群数量的变化往往会直接或间接地影响群落乃至生物圈中其他生物种群数量的变化，与日常生产生活实际联系紧密。因此，本节内容不仅在本章中承上启下，对于本模块也是举足轻重。本部分内容共需要2课时，本节课为第1课时，确定教学内容为： 数学模型的建构、分析及应用。

2 模型建构

建构主义认为，学习者的知识不是通过教师传授获得的，而是学习者借助于他人(包括教师或同学)，利用相关学习资料(书本或其他媒介)，主动建构知识的过程。所谓建构，不只是输入信息，而是加工、分析、选择、重组甚至改造已有的知识经验，最终形成自己的新观点的过程。用于表达生命活动规律的计算公式、函数式，以及由实验数据绘制成的曲线图、柱形图和饼状图等都称为数学模型。数学模型建构的基础是数学方法，有利于提升学生的思维技能，形成简约而严密的逻辑思维品质[2]。

活动1 建构大肠杆菌种群数量增长数学模型。大肠杆菌常通过分裂来增殖，将大肠杆菌接种到液体培养基中，每隔一段时间统计数量，绘制曲线可显示其数量随时间增加的情况： ①如果营养和空间不受限制，每隔20 min大肠杆菌数目加倍。在假设条件下，请你算出1个大肠杆菌产生的后代在不同时间的数量，并填入表1；②请在坐标纸上作图： 为每个坐标轴选择合适的刻度，并在刻度上做记号在图上标出；③请描述自己画出的曲线形状，并尝试说出该种群数量的增长特点。

表1 大肠杆菌数量变化情况记录表

设计意图： 让学生根据材料提供的实例，通过计算、填表和绘图来建构种群数量增长的“J”型曲线(参看图2中曲线A)。让学生先通过自主建构，再小组合作探究，感悟数学模型。

活动2 建构果蝇种群数量增长的数学模型。果蝇繁殖速度快、易计数和保存，常作为生态学研究的材料。实验时，每天将14只发育程度相同的果蝇成虫(雌雄各半)准确地放入相应编号的培养瓶之中。塞住瓶口后，置于相同条件下(25℃恒温培养箱)培养，每隔1 d记录各个瓶中的果蝇成虫数量： ①统计果蝇成虫数量完成表2，并根据数据绘制果蝇种群数量(假设成虫： 幼虫≈2∶5)的增长曲线；②请描述自己画出的曲线形状，尝试说出该种群数量的增长特点；③开放式讨论： 环境中的哪些因素会影响果蝇种群的繁殖？

课前进行了充分的准备工作，包括： 果蝇培养基的配制、果蝇的接种与培养以及果蝇种群数量计数板的设计与制作等。课堂上学生借助于相关用具(毛笔、牙签等)将培养瓶中的果蝇成虫转移到计数板进行数量统计(表2)和数据处理(图1)。

表2 果蝇成虫数量变化情况记录表(11月)

图1 果蝇种群数量变化曲线图注： 第1 d为培养瓶中的果蝇数量，第2 d为培养瓶中的果蝇数量，以此类推

设计意图： 通过小组合作探究，学生自主地体验果蝇培养的过程，参与果蝇成虫数量的统计及种群“S”型增长模型的建构。学生明确并掌握种群“S”型增长的特点等相关基础知识的同时，培养学生的科学思维和科学探究能力。

3 模型分析

模型分析即借助于模型，细致地寻找能够解决实际问题的主线，并通过分析问题最终解决问题的一种科学思维活动。本节课由于时间和空间的限制，为了让学生在课堂上能分析一个果蝇种群的数量随时间变化的规律，教师让学生统计不同时间接种，但在相同条件下培养的不同种群数量来模拟同一种群随时间变化的情况。

活动3 对学生进行批判性思维的训练。有兴趣小组的学生连续20 d培养20个果蝇种群，数量统计如表3。通过小组合作讨论并完成下列问题： ①结合构建的“J”型及“S”型增长模型(图2)，尝试分析种群数量变化的原因；②在种群数量减少时，怎样做可能使种群开始增长？

表3 果蝇成虫数量变化情况记录表

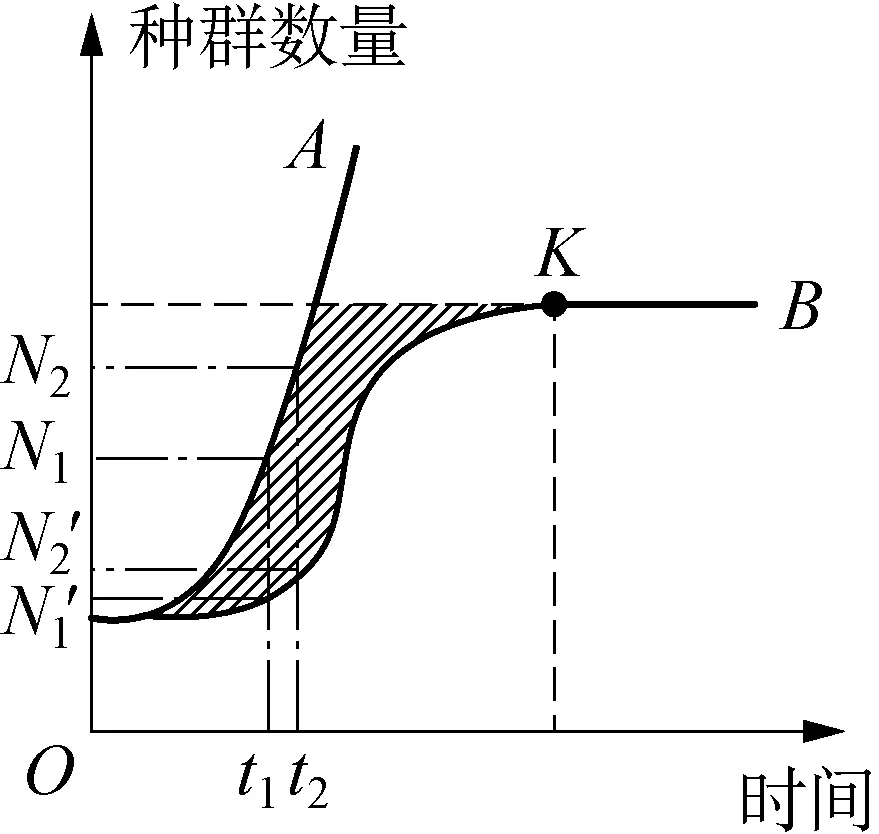
图2 种群数量变化的两种增长曲线

设计意图： 引导学生分析进一步探究实验条件下(连续培养果蝇20 d)曲线的变化趋势。学生依据活动1和活动2的实例提供的两种不同情境，结合构建的“J”型及“S”型增长数学模型分析得知： 培养早期由于食物和空间条件充裕，气候适宜，种群数量急剧增长；培养的中后期由于受到资源和空间的限制，种内斗争也在加剧，种群会停止增长并稳定在一定水平；随着时间的推移，培养末期的不利生存条件最终会导致种群数量急剧下降甚至消亡。

活动4 比较“J”型及“S”型曲线的差异。假设图2中A、 B是果蝇种群的两种增长曲线，请讨论并回答下列问题： ①曲线A、 B所示的增长方式分别在什么情况下发生？②请依据所学知识，尝试说出图中(N1-N1′)以及(N2-N2′)的含义。③尝试说出阴影部分所表示的含义。

设计意图： 在一系列问题的设置中，学生通过比较及归纳等分析方法，厘清了两种增长曲线的适用范围。同时，问题②为问题③作铺垫，让学生对“J”型及“S”型曲线的差异进行更透彻的分析，并得出结论： 阴影部分即表示现实条件中通过生存斗争而被淘汰的个体。

4 模型应用

模型应用是指将所学知识运用于新的具体情境，包括原则、方法和规律的拓展。它代表较高水平的学习成果，需要建立在对知识点掌握的基础之上。而引导学生应用数学模型方法解释生命现象，揭示生命活动的规律是构建数学模型的着眼点。教师要引导学生在现实生活背景中学习生物学，并指导学生应用获取的生物学知识指导生产实践，解决实际问题。

活动5 ①资料1： 老鼠繁殖次数多、孕期短、产仔率高和性成熟快，数量能在短期内急剧增加。其适应性很强，常对农业生产酿成巨大灾害。人们通常通过器械、药物进行捕杀，但种群数量又很快恢复。因此，这种方法是治标但不治本。②资料2： 一位大熊猫研究专家发现： 由于栖息地减少和偷猎者的双重打击，白头叶猴的数量比大熊猫还稀少。他建议要限制农民上山砍柴，并关闭采石场。最近报道，该地约20 km2的研究基地内，白头叶猴已达800只左右。③资料3： 图3所示的曲线可用于指导渔业捕捞，保证鱼类资源的可持续发展。

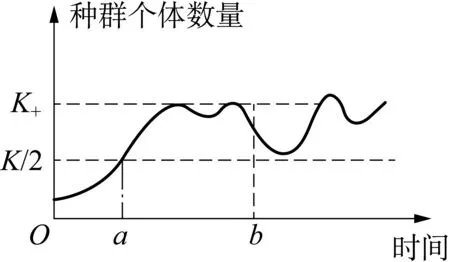
图3 种群个体数量随时间变化的曲线

根据资料进行分析讨论。分析上述3则资料，指导学生进行开放式讨论： ①为达到既治标又治本，试从环境容纳量的角度思考可通过哪些措施控制鼠害？②结合资料2说说我国对大熊猫、白头叶猴等珍稀动物的保护采取了哪些有效措施？其原理是什么？③渔业捕捞时，既要获得鱼类资源较大捕捞量，又要保证其高速增长。分析资料3，说说种群数量在何区间可以开捕？捕捞后剩余量宜为多少？

设计意图： 在学生对J”型及“S”型增长数学模型有了感性和理性认识之后，结合相关资料，进一步运用严密的数学模型思维分析并解决具体问题。例如，通过改变环境容纳量(K值)来有效地控制老鼠等有害动物的数量，来拯救大熊猫等濒危的珍稀物种；在种群增长速度最快且种群数量恢复也较快的K/2值合理进行鱼类资源的捕捞，以实现资源的可持续利用。这一系列实例都是种群数量“S”型增长数学模型在生产生活中的具体应用。

5 教学反思

本节课采用的“建模—析模—用模”教学策略，是数学模型在生物学研究中的一个典型例子，应该使学生举一反三，不断尝试将数学方法渗透进生物学学科的学习中。数学模型的建构体现了跨学科的思想，用数学模型方法来反映生命活动的规律，更容易被学生接受，可起到事半功倍的效果。