一种基于泰勒级数展开的卫星FDOA地面干扰源定位算法

张 威，马 宏，吴 涛，李贵新

(航天工程大学 电子与光学工程系,北京 101416)

0 引言

随着空间应用研究的不断拓展，空间系统正朝着空间组网的方向迅速发展，呈现出海量空间布点、分布式星群组网和立体多层分布的新发展趋势[1-2]，对卫星的管理控制带来了巨大的挑战。由于卫星数量的急剧增长、地面无线设施的普遍使用，卫星在轨运行所面临的电磁环境日益恶化，很容易受到各种辐射源有意或无意的干扰。那么，如何利用干扰信号的特点，对卫星干扰源进行准确、快速的定位，是卫星管理控制中需要解决的关键问题之一。

由于卫星干扰源是非合作对象，所以对其定位是被动定位[3-4]。目前对卫星干扰源进行定位主要是利用干扰信号到达受扰卫星及其邻星的信号参数，主要包括干扰信号的到达时差(Time Difference of Arrival，TDOA)和干扰信号的到达频差(Frequency Difference of Arrival,FDOA)[5-8]。基于干扰信号到达时差的定位技术，以美国海军海洋监视系统“NOSS”系列卫星为典型代表[9]。TDOA定位技术已经相对成熟，主要的算法有平面相交[10]、球面相交[11]、球面内插[12]、泰勒级数[13]、最小二乘[14]、粒子滤波[15]和二次优化[16]。而基于信号到达频差的定位方程较为复杂，解算较为困难。但随着定位参数测量技术的发展，FDOA定位技术成为目前卫星无源定位技术研究的热点之一。目前有文献[17]对仅利用FDOA的辐射定位技术进行研究，但其解算方式采用的是牛顿迭代方式，定位过程中综合利用了多个辐射源。

由于FDOA定位方程组一般具有非线性的特点，泰勒级数展开算法是求解非线性方程的有效方法，具有精度高、顽健性强等特性。而传统的泰勒级数展开算法[10]针对的是无地球面约束的定位方程组，需要3个以上独立的FDOA测量值，但被定位目标往往位于地球表面，引入地球面的约束条件与FDOA测量值构成定位方程组，可以有效增加定位精度，减少有效定位最小观测卫星数量。本文针对含有地球面约束条件的FDOA定位方程组，研究该方程组泰勒级数展开算法的求解方法，推导了详细的求解过程，并对算法的性能进行了分析和仿真评估。

1 FDOA定位方程

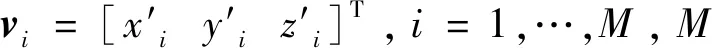
(1)

式中，fc为辐射源信号载波频率，c为信号传播速度，假设地球半径为R，将地球面的约束条件引入FDOA定位方程组，则定位方程如式(2)：

(2)

式中，ΔF1i为FDOA参数，ΔF1i=Δfi-Δf1。

2 算法描述

根据式(2)，对于一组FDOA参数估计结果，存在式(3)中所示的关系式：

(3)

其中，

即卫星si与地面辐射源u之间的距离。泰勒级数展开算法需要一个初始估计位置，由于各观测卫星能同时接收到辐射源信号，则辐射源必然位于各观测卫星的共视区，取卫星共视区内的某一地面接收站的位置ur=[xryrzr]T作为初始估计位置(x(1),y(1),z(1))，将增大算法收敛的概率，将式(3)在初始位置(x(1),y(1),z(1))进行泰勒级数展开，忽略二阶以上的分量，得到式(4)为：

ψ1=h1-G1δ1，

(4)

其中,

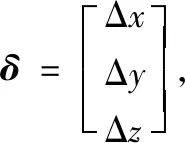
(5)

(6)

其中，对应量为：

(7)

式中，

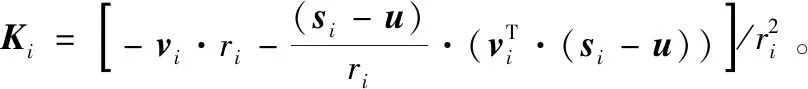
式(4)的加权最小二乘解如式(8)所示，

(8)

式中，Qf为FDOA测量值的协方差矩阵。由于所有的FDOA测量值有一个公共的主星多普勒频移做参考，因此各个ΔF1i之间具有一定的相关性，因此FDOA的协方差矩阵Qf如式(9)所示：

(9)

式中，σ2为FDOA的测量误差方差。

uTu=R2。

(10)

ψ2=h2-G2δ2，

(11)

其中

(12)

(13)

(14)

(15)

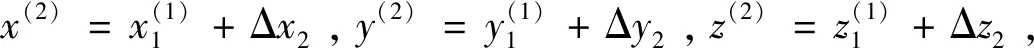
3 算法性能仿真分析

3.1 均方根定位误差与克拉美罗下限

为了更好地评价算法性能，引入2个概念，分别为均方根定位误差(Root Mean Square Error，RMSE)与FDOA定位算法的克拉美罗下限(Cramer-Rao Lower Bound，CRLB)，表达式如式(16)和式(17)所示：

(16)

式中，(x0,y0,z0)为辐射源的真实位置，(x,y,z)则为辐射源估计位置。

(17)

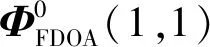
(18)

式中，JFDOA为FDOA定位算法的Fisher信息矩阵，如式(19)所示：

(19)

(20)

式中，F为与约束有关的未知参数的梯度矩阵，当F为零向量时，式(20)退化为式(18)，对于有地球约束的FDOA定位，F=[2x0,2y0,2z0]T，CRLB是任何无偏参数估计均方根误差的下限。

3.2 仿真分析

为便于仿真，选取4颗高轨观测卫星的星历，如表1所示，辐射源位于广州(东经113.3°、北纬23.1°、高程0 km)，地面接收站位于北京(东经116.4°、北纬39.9°、高程0 km)，设FDOA测量时刻为1 Jul 2011 12:00:00.000，则经过计算可得，卫星、辐射源及地面接收站该时刻在ECEF坐标系中的位置矢量如表2所示，卫星的速度矢量如表3所示。

表1 4颗观测卫星的星历

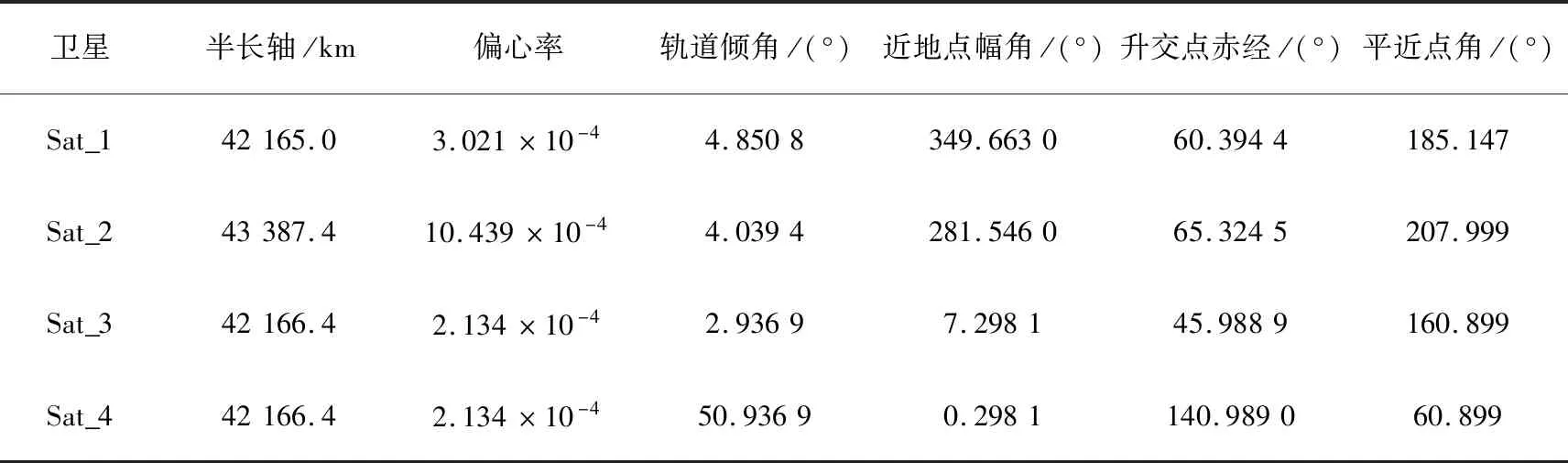
卫星半长轴/km偏心率轨道倾角/(°)近地点幅角/(°)升交点赤经/(°)平近点角/(°)Sat_142165.03.021×10-44.8508349.663060.3944185.147Sat_243387.410.439×10-44.0394281.546065.3245207.999Sat_342166.42.134×10-42.93697.298145.9889160.899Sat_442166.42.134×10-450.93690.2981140.989060.899

表2 FDOA测量时刻卫星、辐射源及地面接收站在ECEF坐标系下的位置矢量

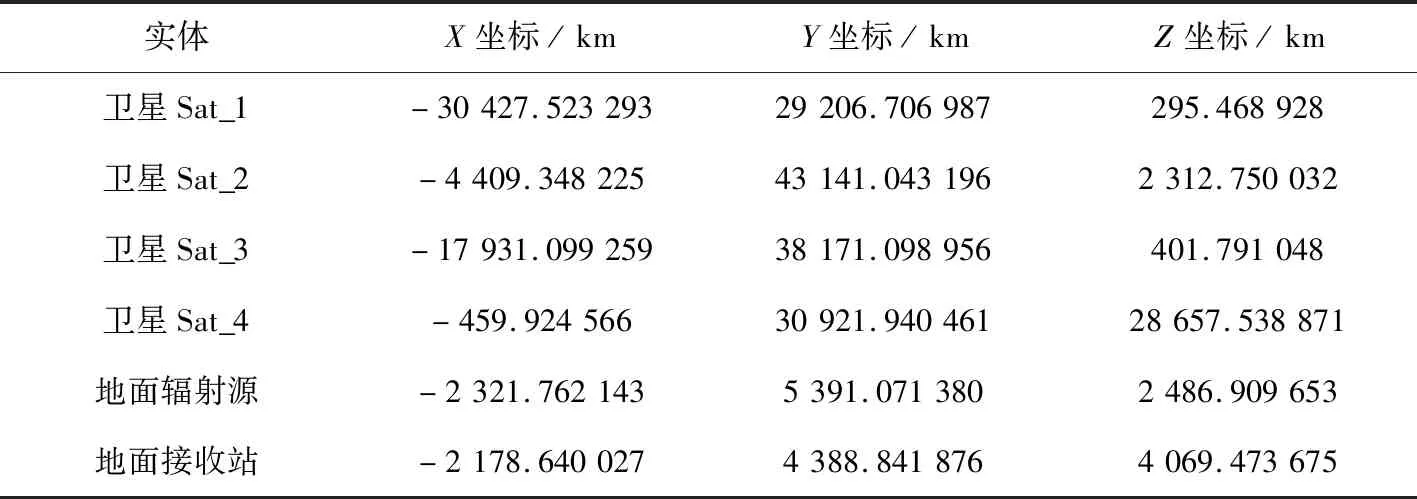
实体X坐标/kmY坐标/kmZ坐标/km卫星Sat_1-30427.52329329206.706987295.468928卫星Sat_2-4409.34822543141.0431962312.750032卫星Sat_3-17931.09925938171.098956401.791048卫星Sat_4-459.92456630921.94046128657.538871地面辐射源-2321.7621435391.0713802486.909653地面接收站-2178.6400274388.8418764069.473675

表3 FDOA测量时刻卫星在ECEF坐标系下的速度矢量

卫星X′坐标/km·s-1Y′坐标/km·s-1Z′坐标/km·s-1Sat_10.0074470.010227-0.255939Sat_20.1357870.019613-0.134817Sat_30.0039150.003678-0.152160Sat_4-0.373110-1.0720971.151666

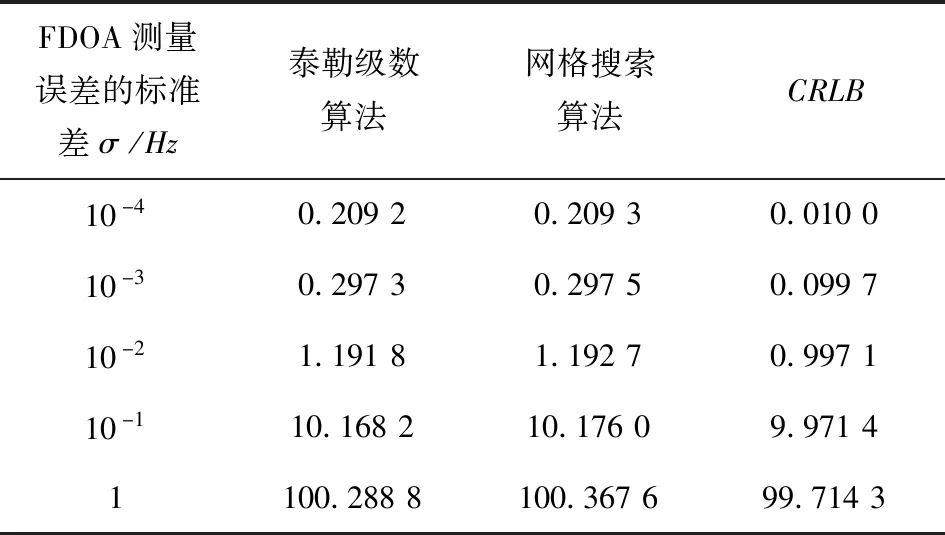
表4 σ不同取值情况下各算法的RMSE km

由表4可见，泰勒级数展开算法及基于网格搜索的最大似然算法在所给的FDOA测量误差情况下都能较好地接近克拉美罗下限，但本文研究的泰勒级数算法性能要略好于网格搜索算法。

表5σ=10-2Hz时2种算法的迭代性能比较

算法迭代次数迭代时间/ms泰勒级数算法1415.625网格搜索算法44640.625

由表5可见，泰勒级数算法无论在迭代次数与迭代时间上都优于网格搜索算法。

图1给出了泰勒级数展开算法、基于网格搜索的最大似然算法与CRLB曲线的比较，其中RMSE单位为km，σ单位为Hz。由图1可知，泰勒级数展开算法与基于网格搜索的最大似然算法的定位性能非常接近，二者在FDOA测量误差较低时对CRLB的接近性能较差。

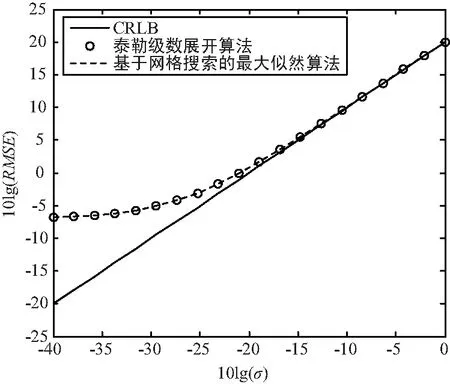
图1 各FDOA定位算法性能对比图

当观测卫星为4颗时，即Sat_1,Sat_2,Sat_3,Sat_4，对比有、无地球约束时，泰勒级数展开算法的性能。表6给出了2种情况下不同σ时的RMSE，其中，RMSE均为5 000次独立实验的统计结果。图2给出了2种情况下泰勒级数算法与CRLB曲线的比较，其中RMSE单位为km，σ单位为Hz。

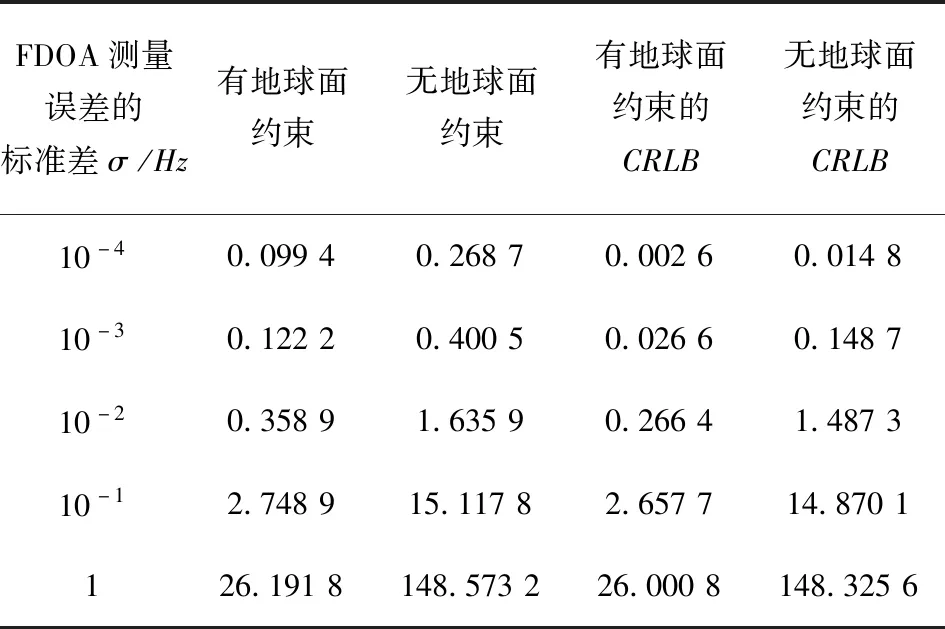
表6 σ不同取值情况下各算法的RMSE km

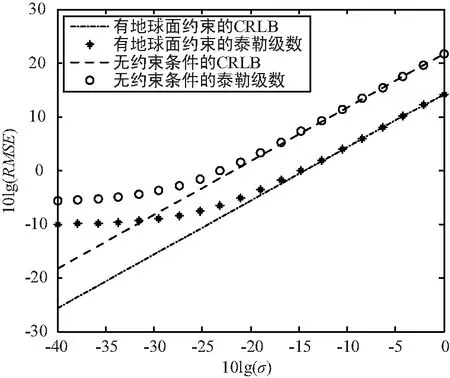
图2 有、无地球面约束条件下泰勒级数展开定位算法性能对比图

由表6及图2可见，当观测卫星数目不变时，加入地球面约束的泰勒级数展开定位算法能够明显地提高普通泰勒算法的定位精度，并且能有效逼近克拉美罗界。仿真结果中FDOA测量误差的标准差σ较低时2种算法的RMSE与CRLB之间的偏离较大，本文总结其主要原因为仿真中一些固定参数的选取误差，如地球半径、地球椭圆偏心率及坐标系转换中的春分点角等参数的选取误差。

4 结束语

本文提出一种基于地球面约束的泰勒级数FDOA定位算法，经过理论和仿真分析，获得了如下结论：加入地球面的约束条件可以有效减少定位卫星的需求数目，提高FDOA定位的定位精度，该算法能够有效逼近CRLB，是最优的定位估计器。根据多次仿真结果可知，该算法收敛速度快且定位性能略优于网格搜索算法，可以用于实际工程，为研究FDOA定位的相关人员提供一定的参考。