天线相位中心实测技术研究*

舒应超，吴禄军

（中国电子科技集团公司第二十七研究所，河南 郑州 450047）

0 引 言

对于大多数的天线而言，设计人员主要关心的是它在远场的幅度方向图、增益、副瓣电平和极化形式等电参数，而对它的远场相位方向图关注较少[1-3]。但在有些情况下，例如在关注天线的相位中心特性时，天线的相位方向图就成为我们必须加以研究和分析的特性。天线相位中心的定义是：在天线上或其周围存在一个点，该点可使天线远场主瓣内的相位分布是一个常数[4-5]。实际上，天线的远场相位方向函数大都是依靠测量或者考虑种种误差计算获得的，所以都不会是一个常数，而是有起伏的。所以，我们定义一个可使天线远场主瓣内的相位分布最平坦的点，称该点为视在相位中心，简称视在相心[3，6]。对于实际的天线，我们所能得到的就是视在相心。所以，测量天线相位中心的过程实际上就是寻找其视在相心的过程。

1 基本理论分析

如图1所示，在相位中心的实际测量过程中，被测天线架设于测试转台上，天线相位中心与转轴中心有一定的位置矢量（用R′表示）探头几何中心与被测天线几何中心位于一条轴线上（记做Z轴），探头测量采样轨迹平行于X轴、Y轴、同时被测天线口面垂直于地平面，因此转台、探头、被测天线三者处于三个相关坐标系中；如图2所示[7]。

图1 被测天线在暗室内实际测量情况示意图

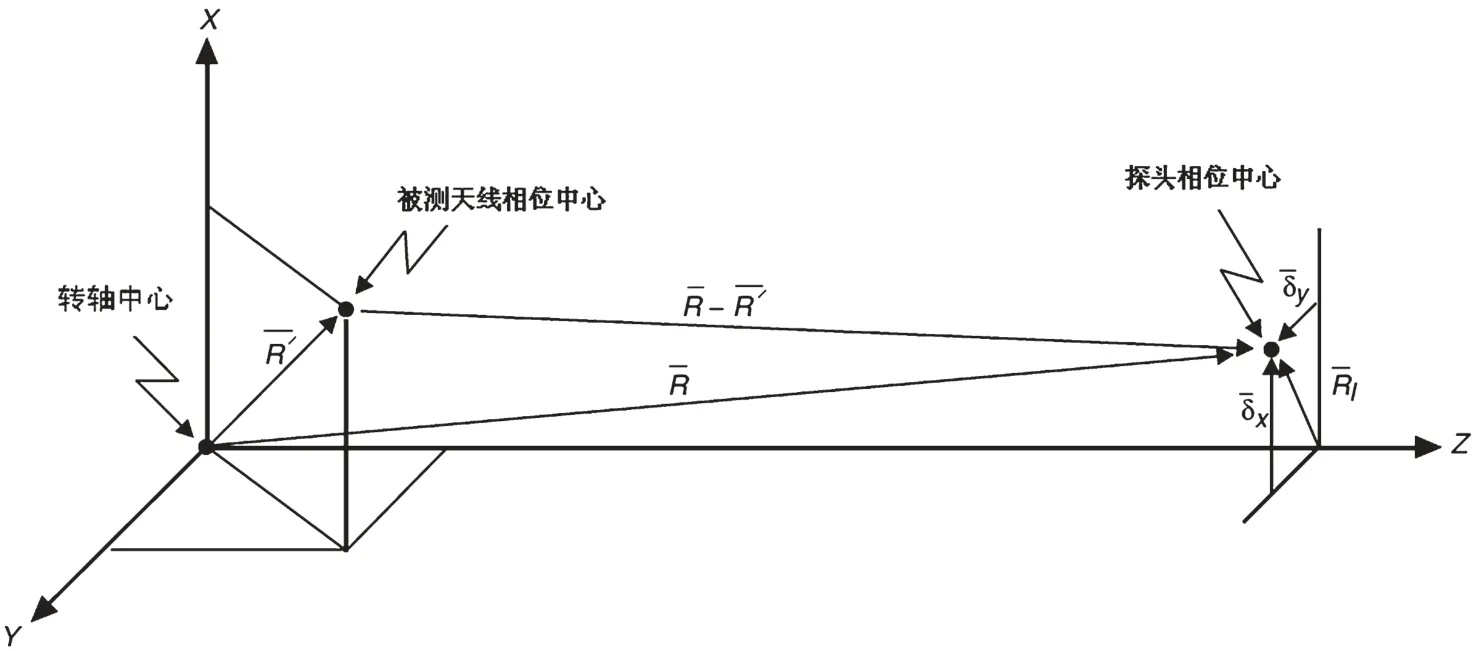
图2 相关坐标系下转台、探头、被测天线相对位置示意图

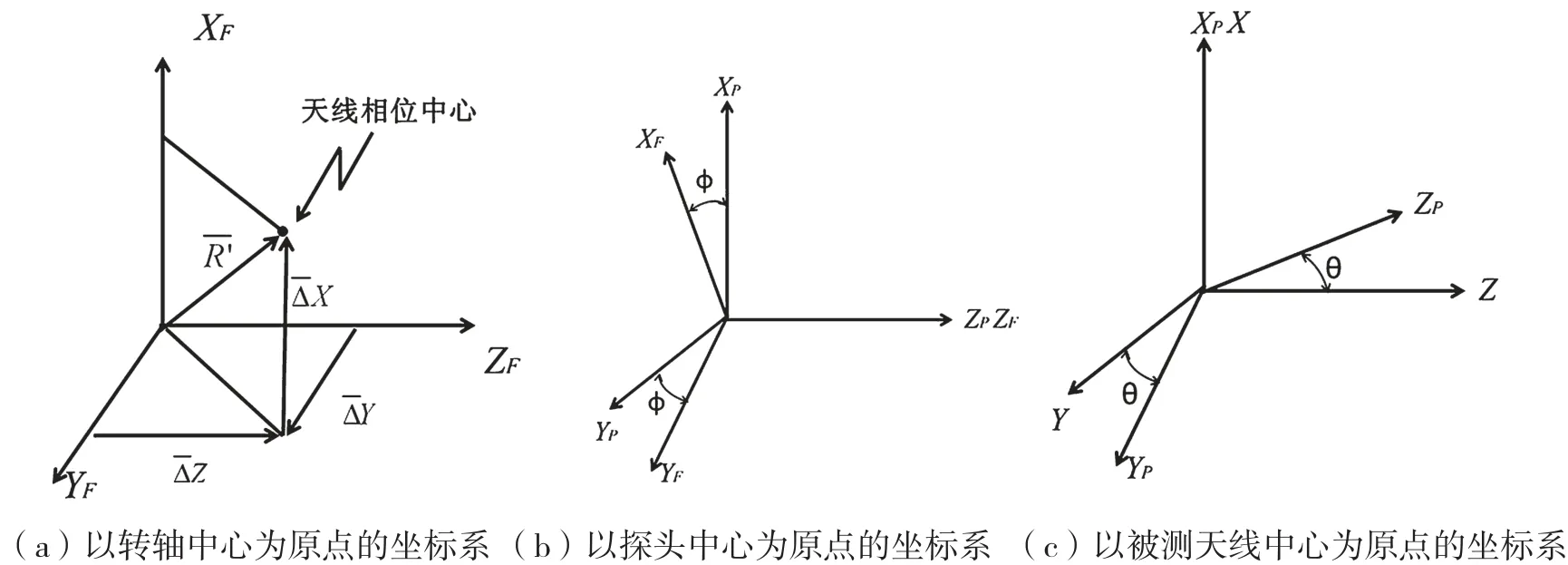
实际测量情况下转台、探头、被测天线在各自坐标系下的运动情况如图2所示，因为三者处于相关坐标系中，三个坐标系之间有如下转换关系：

其中，上标代表单位矢量。

在实际的天线测量中（相位方向图及辐射方向图的获取），一般由探头发射信号，被测天线在测试转台上转动（也即是通过变化角度θ，此时保持φ值不变）而获取不同位置的幅度与相位信息。此时，如图3（a）所示，我们将被测天线的实际相位中心与转轴中心之间的位置差以矢量形式可以表示为：

同样的，将探头相位中心与Z轴之间的位置差以矢量形式表示为：

由于被测天线的相位中心并不位于测试转台的转轴中心，以及探头的相位中心并不位于Z轴；所以在进行天线相位中心测量时将不可避免的引入测量误差。假设该误差为包含ejwt的时谐量，那么被测天线的相位方向图函数将表示为：

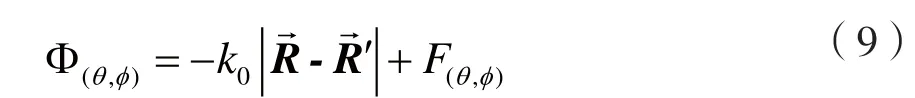
其中，k0为自由空间波数，（k0=（2π/λ0），λ0为自由空间波波长）， F(θ,φ)为被测天线的相位中心位于测试转台的转轴中心时的相位方向图，利用式（7）和式（8），以及图2和图3中各个量之间的关系，可以得到：

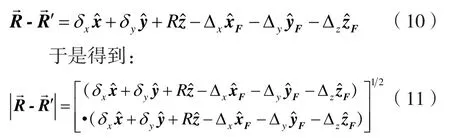
整合式（1）～式（6），可以得到：

式（15）进一步整理成：

考虑到在实际测量过程中 Δx、Δy、Δz、δx、δy远小于R，因此式（16）近似等于：

对比式（16）和式（17）可以看到，δx、δy由于具有远大于其值的R2作为分母，所以其影响可以忽略不计。将式（17）带入式（9）得到：

通过式（18）可以得到如下结论:测量得到的相位方向图Φ(θ,φ)表面上是相位关于 θ、φ的函数，其实最终决定因素依赖于Δx、Δy、Δz三个变量，也即是相位中心与转轴中心坐标系原点的偏移量；

2 相位中心的求取

对于被测天线来讲，可以认为它发出的是一个近似完美的球面波，那么它的真实相位方向图 F(θ,φ)可以认为是一个与θ，φ无关的常量；在一个既定的测量过程中（R为定值）-k0R也为一个常量。因此我们将[F(θ,φ)-k0R]记为常量C，那么式子（18）就可以表述为：

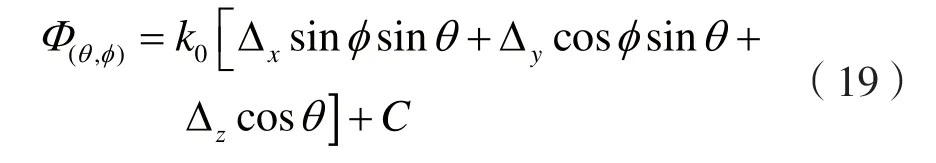
在实际的相位方向图测量过程中，以线极化化天线为例，首先保证待测天线与探头极化匹配（φ为极化对准时的偏转角），然后转动转台得到相位Φ(θ,φ)随角度θ变化的函数。也即是在保持φ值不变的情况下，得到一组相位Φ(θ,φ)关于 θ 的值，因此Φ(θ,φ)为一个既定φ值下 θ 的函数，

根据测量得到的辐射方向图（相位方向图采样测量时可同时得到）确定该待测天线的半功率波束宽度，然后在半功率波束宽度内选取4个点，即4个θ值，分别带入后得到一组方程：

下面将第三节讨论的三种情况组合为含有变量Δx、Δy、Δz的三个方程：

根据远场二维相位数据，可通过求解这一组方程，得到Δx、Δy、Δz和常量C。可以确定的一点是使用不同的θ与φ计算得到的相位中心坐标都不相同，远场相对这些相位中心的相位都近似相等，这些点都是近似满足相位中心条件的点，这些点组成的区域就是相位中心区域，远场相对这个区域内的任何一个点的相位都近似相等。为了获得较为近似的相位中心点，我们可以使用多次测量求均方根值的方法确定一个点，将该点定为我们要找的相位中心点。

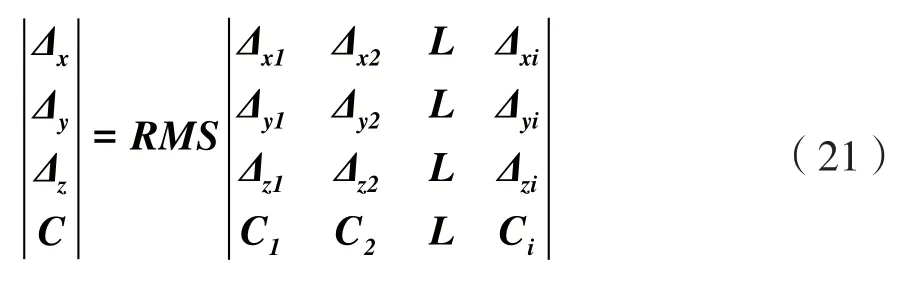
3 实际应用

在实际测量过程中，φ一般很难随意取值，通常都会选定φ=0°和φ=90°两种情况（垂直极化和水平极化状态），对应的相位方向图方程表述为：

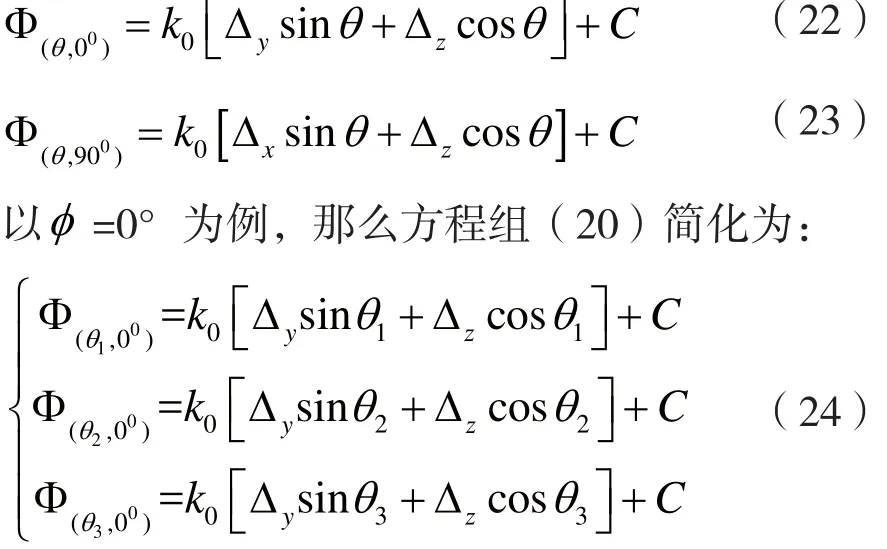
以工作在6.2 GHz频点的一个天线为例，通过实际测量，选取多组数据求解天线相位中心点，最后利用式（21）处理这些相位中心点，得到一个最接近的相位中心点。

参照计算得到的天线相位中心点，微调待测天线的位置，再次测量相位方向图（参见图4），可以看到调整后的相位方向图平坦很多。

图4 前后两次相位方向图对比

4 结 语

虽然天线相位中心的精确获取难度较大，但是通过多次测量，多次求解相位中心，获得多个相位中心点，然后对这些相位中心点求取均方根值，可以获得一个较为精确的相位中心，该方法对相位中心的精确测量具有一定的实用意义。