SACS软件考虑波纹板强度的结构设计方法研究

■ 海洋石油工程股份有限公司 尹光荣 杨俊 温生亮 李拓夷

波纹式板材，简称波纹板，其截面一般为梯形或者弧形，有的也带有卷边或者加劲肋，一般是由平钢板经辊压冷弯而成，以板的折曲来代替加强筋的作用，提高其面外刚度和稳定性，具有轻质、高强、美观、耐用、施工简便、抗震等优点，在建筑、船舶与海洋工程、航空航天等行业应用广泛。

生活楼模块是海洋石油钻采平台上保障海洋石油生产和人员生活的重要结构物，一般生活楼内外墙壁均采用梯形波纹板设计建造。目前，国内海洋固定平台生活楼的设计仍以传统的框架加斜撑型式为主，不考虑钢质内外墙壁的刚度贡献，也不核算其设计强度和稳定性。传统的设计方法与假定条件导致结构用钢量大，不仅浪费材料，而且加工工艺复杂，增加设计与预制施工的难度和工作量，影响生活楼的内外舾装工作[1]。

已有的海洋结构物设计和建造经验表明，与四周梁柱框架可靠连接的钢质波纹板内外墙壁因其具有较大的面内抗剪能力，可对主体框架结构起到较大的加强作用，以提高结构的空间整体性。因此，在生活楼结构设计时考虑波纹板贡献，对提高主框架刚度和强度，以及优化生活楼结构均具有重要意义[1]。但目前应用于生活楼波纹板的设计准则和校核方法还不够完善，本文以某平台生活楼的梯形波纹板设计研究成果为依据，较为完善地提出了波纹板结构设计方法，用于指导设计人员开展波纹板设计工作（图1）。

1.波纹板计算模型

波纹板结构可以是全尺寸建模，也可以等效为正交各向异性平板。全尺寸建模复杂费时、网格和单元较多，对计算机性能要求高，该方法一般用于精细的局部分析，以及作为对比验证分析的基准模型。等效为正交各向异性平板方法在保证模拟精度的情况下，能够大大减少建模工作量，降低对计算机的需求，适合工程应用[1]-[3]。

1.1 正交各向异性平板的弹性理论

依据经典弹性理论，正交各向异性板平面应力状态下的应力ü应变关系为：

式中，Exx、 Eyy分别为局部坐标下x、y轴方向的弹性模量；μxy为局部坐标下x轴方向泊松比，指在单轴作用下x向的单位拉/压应变导致的y向压/拉应变；μyx是与μxy垂直方向的泊松比。Exy为等效剪切模量。

依据相关文献可知，对于四周与框架有效连接的波纹板，各参数计算公式为[1]-[6]：

式中E0、G0、μ0为波纹板材料的弹性模量、剪切模量、泊松比，I0为等效正交各向异性板关于x轴（截面中性轴）的惯性矩，Ix为波纹板关于x轴（截面中性轴）的惯性矩，其他符号见图2。对于正交各向异性平板的静力平衡方程、几何方程以及边界条件的处理，与普通的弹性理论平面应力问题一致。

图2 波纹板和等效正交异性板

1.2 正交各向异性平板的有限元理论

有限元法每个单元{Fe}和位移{δe}的一般表达式为[7]：

式中，[Ke]为单元刚度矩阵，其一般形式为：

式中，[B]称为“几何矩阵”，表征节点位移与节点应变之间关系。[D]称为“弹性矩阵”，表征节点应变与节点应力之间的关系。V为单元体积。

对于平面等厚单元，[B]不随x、y变化，且[D]为常数，上式可以简化为：

式中，Δ为板单元面积。单元刚度矩阵可表达为：

式中，Bx、Bμ、By为拉压刚度，Bxy为剪切刚度，Dx、Dμ、Dy为弯曲刚度，Dxy为扭转刚度。

波纹板不同的边界条件、波形和假定条件，都会影响刚度矩阵表达式[4]-[6]，这里仅给出Samanta和Mukhopadhyay对四周有效支撑梯形波纹板的推导结果，如表1所示：

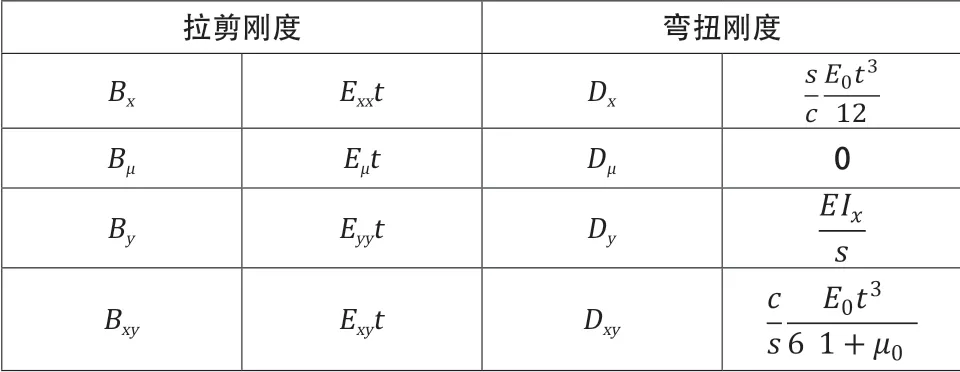
表1 Samanta和Mukhopadhyay给出的刚度矩阵表达式

1.3 软件计算对比验证

SACS和ANSYS是海洋结构物设计常用软件，SACS自带的加筋板模块能够自动将波纹板等效为正交各向异性板，ANSYS则能够方便建立全尺寸的基准模型。本节用ANSYS全尺寸模型来验证SACS等效模型的准确性。

图3 波纹板尺寸

以门型框架为例，框架立柱为Ф610×19/25mm，框架型钢为H300，波纹板尺寸如图3所示。框架顶部型钢受55kN/m竖直向下线荷载，立柱底部固定约束，详见图4。表2结果表明，两种建模方法位移和应力相符，如图5所示。SACS等效方法能够较准确地模拟波纹板刚度，推荐设计使用。

图4 门型框架ANSYS和SACS模型

图5 ANSYS和SACS计算位移和等效应力对比

表2 ANSYS与SACS计算对比

2.波纹板强度校核

通过SACS软件建立合理的波纹板计算模型进行计算分析，可得到波纹板的内力、位移、应力和应变等结果。将这些结果带入规范公式进行验算，可验证波纹板设计是否满足规范要求。一般来说，波纹板强度校核有以下几种方法。

2.1 等效构件强度

波纹板可取一个波距截面等效为单槽梁构件，按照规范要求计算截面特性，再按照构件强度或者构件承载力公式校核其拉弯或压弯组合作用下的强度，这种方法称为等效构件强度校核。比如，槽型波纹板可将截面等效为或型单槽梁构件[8]。

2.2 板的屈服强度

全尺寸建模的波纹板可以按照板格的屈服失效准则来校核其强度。按照第1.3节结论，采用SACS等效为正交各向异性平板建模也可以采用这种方法。

板材屈服校核要求为：

式中，σ0为槽翼板或槽腹板的屈服强度，SF为安全系数，σeq为等效米塞斯应力（von-mises stress），一般取板单元形心处的中面应力（薄膜应力）。如果σeq不能直接获得，也可通过下式计算：

式中，σx和σy为板单元x、y方向的应力，τxy为板单元xy方向的剪应力[9]。

3.波纹板屈曲校核

图6 翼板和腹板的有效宽度示意图

波纹板的屈曲校核可以从等效构件和板格两个角度来考虑。波纹板截面一般为非紧凑截面（a/t或者b/t较大），除了需要考虑整体屈曲校核外，还应考虑翼板和腹板的局部屈曲，并且翼板和腹板还需要考虑有效宽度的折减[10]。（图6）

波纹板的屈曲失效，可能包括槽条的整体柱屈曲、槽条梁翼板的屈曲和槽条梁腹板的屈曲三种情况，其中槽条梁翼板和腹板的屈曲属于局部屈曲[11]。如果等效为正交各向异性平板，还应包括整体板屈曲校核[12]。

3.1 整体柱屈曲

波纹板在轴向压应力作用下的整体屈曲失效可用柱屈曲进行校核，将截面等效为两个1/2翼板和1个腹板组成的槽条构件，如图7所示。轴向受压的槽条构件屈曲衡准要求为：

式中，σcomp为杆件的轴向压应力。[σcr_comp]为受压杆件的许用临界屈曲应力：

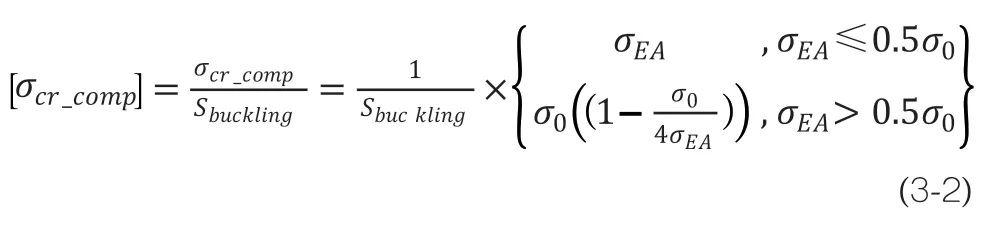
式中，Sbuckling为屈曲安全系数，σ0为杆件屈服应力，σEA为压杆弹性屈曲应力[11]。

图7 槽条构件示意图

3.2 局部屈曲

波纹板的局部屈曲包括每一个翼板和腹板的板格屈曲。这里定义屈曲利用因子为施加的载荷与对应的许用屈曲能力之比，其衡准要求为：

其中，Wact为构件上施加的等效应力，[Wu]为构件在各种屈曲模式下的屈曲能力，Sbuckling为屈曲安全系数，γc为结构发生失效时的应力倍增因子[11]。

对于每一个翼板和腹板，都应满足板的极限应力状态方程：

式中，σx和σy为施加在板格边界上的正应力，τ为施加在板格边界上的剪应力，σcx和σcy为沿着与屈曲板格长边平行方向和短边平行方向的极限屈曲应力，τc为极限屈曲剪应力，B和e0为系数，βP为板的长细比参数，SF为安全系数，γc1，γc2,，γc3，γc4为上述每一个不同极限状态在失效时的应力倍增因子[11]。

3.3 整体板屈曲

波纹板的整体板屈曲是将波纹板整体等效为正交各向异性平板，再用平板的屈曲公式校核整块波纹板的双向受压和受剪，其衡准要求为：

式中，η为最大许用强度利用率系数，σGx和σGy为在波纹传播方向和波纹垂直方向轴向受压极限屈曲应力。σGx和σGy的计算考虑了正交各向异性平板等效刚度的影响[12]。

表3 波纹板屈曲校核结果

4.工程应用和结论

在波纹板结构设计时，将其等效为正交各向异性板是可行的。这种方法可以与现有杆梁建模方法相结合，大大简化了建模过程，减少计算工作量。采用SACS波纹板建模方法设计的某平台120人生活楼，优化掉全部斜撑，节省钢材约50吨，占生活楼用钢量约7%，且降低了房间墙壁开门、开窗等舾装工作难度和焊接工作量（图8、表3）。

图8 某平台生活楼计算实例

本文提出了考虑波纹板强度的结构设计方法，该方法可以有效降低钢材消耗量和舾装工作量、提高经济效益，推荐应用于生活楼、组块等海上结构物设计。同时，该方法既可以用于完整建模分析结构设计，也可以用于等效成正交各向异性板建模分析结构设计，具有较强的适用性。