6-DOF工业机器人相贯线焊接运动规划

曾疆伟 周剑秋

中图分类号：TP241.2文献标识码：ADOI：10.3969/j.issn.2096-1553.2019.02.014

文章编号：2096-1553（2019）02-0102-07

关键词：相贯线焊接;6-DOF工业机器人;工件装夹模型;运动规划

Key words：intersection line welding;6-DOF manipulator;model of clamping;motion planning

摘要：针对实际生产中主管与支管间存在一定偏置和倾斜、不适于专用机器人进行相贯线焊缝焊接的问题，通过改善相贯线数学模型，采用D-H参数构建 6-DOF 机器人与变位机模型，给出一种工件装夹模型和模型间的坐标系转换关系，再用主面二分法求解焊缝参数，实现了专用机器人连续焊接作业的运动规划.Matlab仿真结果表明，相贯线轨迹平滑，与实际轮廓基本吻合，证明了该研究方法的正确性.

Abstract：Aiming at the problem of offset and inclination between supervisor and branch pipe in actual production， which is not suitable for special robots to weld intersecting line，the model of 6-DOF mainpulator and positioner with D-H parameterwas constructed through improving the mathematical model of intersecting line， a coordinate transformation relationship between workpiece clamp model and model was put forward， and finally the welding line parameters was solved by main-plane dichotomy method. The motion planning of special robot continuous welding operation was realized. The simulation results of Matlab showed that the intersection trajectory was smooth and basically coincided with the actual contour， which proved the correctness of the research method.

0 引言

目前，基于工業机器人的相贯线焊接在实际应用中越来越普及.机器人焊接时需要确定机器人和焊缝的最佳位姿，以保证焊缝的良好形成.生产实践表明，当焊缝处于船型位姿或者平焊位姿时可以达到最佳的焊接效果[1].文献[2-4]利用视觉伺服对焊接机器人焊缝跟踪进行了研究，但是有视觉伺服控制的机器人系统对控制器性能要求较高，大大增加了生产成本.基于工件模型机器人焊接能在降低生产成本的同时极大地提高焊接效率，国内业界针对管管相贯线焊缝的数学模型和机器人的位姿进行了一定的研究，并研发了一系列相贯线焊接专用机器人[5-7]，但是专用机器人并不适用于相贯线焊缝之外的其他生产场合，这限制了专用机器人的普及和推广.

目前，对于管管相贯线机器人焊接的研究多是针对相贯线特殊情况进行的，即主管与支管正交的情形.但在实际生产过程中，主管与支管一般都存在一定的偏置和倾斜，文献[8]对相贯线的数学模型进行了研究，但是该相贯线数学模型并没有深入分析主管与支管的相对位置关系，以及各个尺寸参数对相贯线形状的影响，因此，在相贯线焊接过程中不能直接用于相贯线焊缝模型的建立.文献[9-10]对变位机和机器人之间的协调运动进行了研究，但是工件相对于变位机的定位方法和确定装夹位置后的坐标变换模型未在文献中提及.鉴于此，本文拟针对一般情况下的相贯线焊缝进行研究，提出相贯线的改进数学模型和工件装夹模型，并用Matlab对相贯线轨迹进行仿真，以期为生产实际中工业机器人相贯线焊缝焊接的实现与推广提供理论基础.

1 相贯线焊缝数学模型的建立

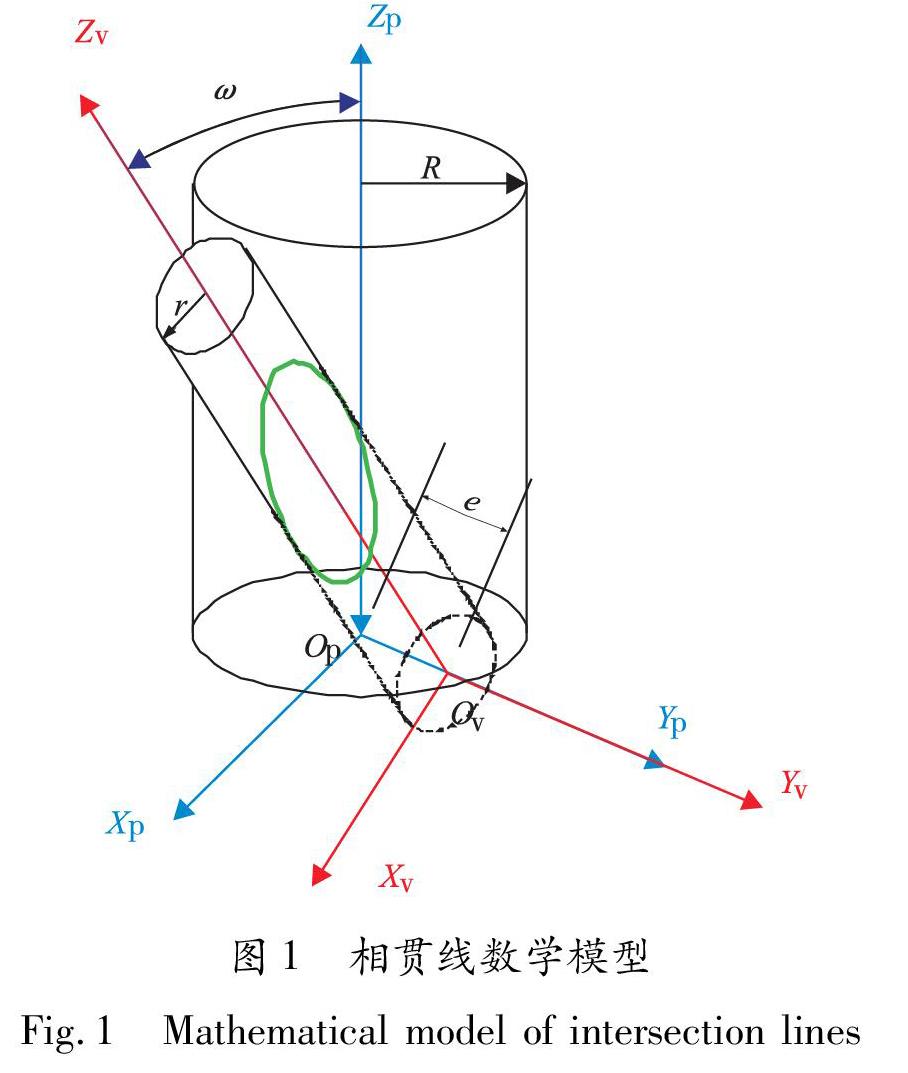
1.1 相贯线数学模型

1.2 相贯线数学模型的改进

2 6-DOF机器人与变位机模型的建立

在笛卡尔空间中描述焊缝和焊枪的姿态各需要3个角度[1]，但在实践中，只需焊缝的倾角和转角就可以将焊缝调节到理想的船型姿态，因选择2自由度变位机就可以把工件调整到理想的焊接位置.焊缝的偏角和焊枪的旋转角更多的是影响机器人的姿态，这也就意味着需要通过这2个参数对机器人关节姿态进行优化，从而确定机器人位姿的最终结果.D-H参数法是一种常用的机器人连杆建模方法，用来描述机器人与变位机之间的坐标关系.6-DOF机器人与变位机笛卡尔空间位置关系如图3所示.

3 机器人焊接运动规划

3.1 坐标系转化关系

计算出6-DOF机器人末端Wt和固定在变位机上工件的Wwp在世界坐标系Ww中的坐标变换矩阵，才能合理规划机器人和变位机在世

wppT，即主管坐标系到工件坐标系的位姿变换矩阵，该变换矩阵会因为工件装夹位置的不同而改变，因此需要确定一种通用的装夹方法来确保不同管径的工件在装夹完成后仍能确定主管坐标系在工件坐标系中的位姿.为了便于统一建模和计算，现规定在主管与支管间偏距e=0和支管倾斜角ω=0时，支管轴线Zv与工件坐标系Wwp的Z轴重合，且主管轴线Zp与工件坐标系的Y轴平行，如图4所示.

由此，主管坐标系WP可由工件坐标系Wwp经过一系列变换得到.沿着主管坐标系WP的ZP轴方向平移R/tanω，沿着YP轴方向平移e，沿XP轴方向平移R，绕Zp轴旋转π/2，最后绕XP轴旋转π/2与工件坐标系Wwp重合.规定沿坐标轴正方向移动为正，沿坐标轴负方向移动为负，顺时针旋转为负，逆时针旋转为正，所以，主管坐标系WP到工件坐标系Wwp的坐标变换矩阵为

3.2 主面二分法求焊缝参数

文献[3]提出了一种通过坐标变换的方式来建立焊缝特征矩阵的方法，并指出了相贯线上任意点的切线始终与过该点的两个圆柱切平面的交线重合.由此可以计算出焊缝处于船型位姿焊接状态所需要的参数、焊缝坐标系Wwd相对于主管坐标系Wp的特征矩阵.焊缝插接主法面二分角示意图如图5所示.

由方向向量S3可得到当前焊点的焊缝倾角θ和焊缝偏角σ.根据文献[1]对焊缝倾角和偏角的定义，设S3在水平面的投影向量 b=[X3，Y3，0]，焊缝偏角σ对焊接无影响，可取任意值，焊缝倾角θ为

通过主面二分法求得焊缝当前焊点关于焊缝3个角度参数θ，σ，φ的位姿矩阵为

将式⑥⑦联立，可求得该焊点处变位机关节位姿矩阵的各元素值，即可将变位机关节参数θ7和θ8用θ，σ，φ 3个角度参数表示.另外，解析法求机器人运动学逆解时可能存在多个计算结果，所以本文采用文献[11]的机器人逆解优化方法求出变位机逆解的唯一解.

同理，利用当前焊点的位置和船型位姿状下焊枪参数α，β，γ，可求得焊枪末端姿态矩阵，然后使其与位姿变换矩阵wtT相等，可用焊枪参数α，β，γ表示机器人各个关节θ1—θ6在当前焊点时的关节角度，最后将焊缝离散后进行插补运算[12-13]，即可规划出关节角关于时间t的连续运动轨迹，从而实现6-DOF机器人的连续焊接作业.

4 仿真验证

为了验证优化相贯线方程的正确性，用Matlab对相贯线轨迹进行了仿真，相贯线参数为ω=pi/2，e=200 mm，r=100 mm，R=300 mm.仿真结果如图6所示.

为了简化仿真模型，仿真过程仅针对相贯线焊接的位置进行研究，而没有对姿态进行规划，但并不影响验证相贯线模型的正确性.从图6可以看出，根据相贯线模型，虽然在Matlab中只得出了一部分轨迹图，但是由于相贯线是对称曲线，所以只需要通过坐标对称即可求出另一半轨迹.

为了使机器人运动轨迹更加直观，将相贯线轨迹离散插补后用Matlab toolbox工具仿真出部分相贯线运动轨迹，如图7所示.由图7可以看出，相贯线轨迹平滑，基本与实际轮廓吻合，验证了所建立相贯线模型和通用工件装夹数学模型的正确性.

5 結论

目前专用机器人进行插接管相贯线焊接，大多适用于主管与支管正交的情形，但实际生产过程中主管与支管间通常存在一定的偏置和倾斜.针对这个问题，本文在对主管与支管非正交情况下的相贯线焊缝进行研究的基础上，改善了相贯线数学模型，然后采用D-H参数建立6-DOF机器人与变位机模型，给出工件装夹模型与模型间的坐标系转换关系，用主面二分法求解焊缝参数，实现了专用机器人连续焊接作业的运动规划.

用Matlab机器人工具箱对焊缝模型和机器人运动规划进行了仿真，结果表明，相贯线轨迹平滑，与实际轮廓吻合，证明了所提出改进的相贯线和通用的工件装夹数学模型的正确性.

本文为管管想贯线焊接的离线编程提供了理论基础.本文所提出的方法是在仿真环境中进行的，下一步工作将在实际生产中验证该方法的可行性.

参考文献：

[1] 王晓峰，陈焕明，江淑园.焊接位姿参数定义的讨论及典型工件的建模[J].南昌航空工业学院学报（自然科学版），2006，20（2）：24.

[2] ZHOU L，LIN T，CHEN S B.Autonomous acquisition of seam coordinates for arc welding robot based on visual servoing[J].Journal of Intelli-gent and Robotic Systems，2006，47（3）：239.

[3] LUO H，CHEN X.Laser visual sensing for seam tracking in robotic arc welding of titanium alloys[J].The International Journal of Advanced Manufacturing Technology，2005，26（9/10）：1012.

[4] YE Z，FAND G，CHEN S，et al.Passive vision based seam tracking system for pulse-MAG welding[J].The International Journal of Advanced Manufacturing Technology，2013，67（9/12）：1987.

[5] 汪苏，韩凌攀，苗兴刚，等.相贯线焊接机器人示教再现的工程化实现方法[J].上海交通大学学报，2010（S1）：138.

[6] 苗新刚，汪苏，李晓辉.大构件相贯线焊缝轨迹拟合方法[J].焊接学报，2011（1）：89.

[7] 杜宏旺，王宗义，刘少刚，等.接管焊接机器人运动学及轨迹修正[J].焊接学报，2009（7）：45.

[8] 张晓东，王园宇，郝鹏飞，等.相贯线及其展开曲线的方程构建方法的研究[J].机械设计与研究，2008（2）：21.

[9] 张毅，张旭，罗元.不规则管管相贯曲线的轨迹规划[J].华中科技大学学报（自然科学版），2015（S1）：276.

[10]唐创奇，孟正大.弧焊机器人与变位机协调运动的实现[J].工业控制计算机，2008（1）：47.

[11]何广忠，高洪明，吴林.基于焊接位置数学模型的变位机逆运动学算法[J].机械工程学报，2006（6）：86.

[12]胡绳荪，申俊琦，陈昌亮，等.基于B样条空间等距线的机器人轨迹优化算法[J].天津大学学报（自然科学与工程技术版），2015（8）：723.

[13]霍孟友，王新刚，尹萍.自动焊接相贯线接缝的实时插补控制算法与仿真[J].焊接学报，2006（11）：37.