深部巷道开挖加卸荷诱发围岩失稳的模拟研究

靳西传，周宗红，龙 刚，侯廷凯

(1.昆明理工大学国土资源工程学院，云南 昆明 650093；2.桐梓煤电化循环经济工业园区管理服务中心，贵州 桐梓 563200)

0 引 言

随着浅部矿产资源的枯竭，深部开采将成为趋势与常态。目前，国外金属矿山开采深度已超过4 350 m，国内金属矿山也逐渐步入1 000～2 000 m的深度开采阶段[1]，深部开采的变形破坏机理与浅部有着很大的差异，因此，众多学者通过各种方式进行大量实验、监测来探究深部巷道围岩的力学特征，取得了巨大成就。但受到试验周期长、费用高和无法大规模使用的限制，数值模拟进入了视野，并伴随计算机的迅猛发展以及越来越高的计算精度和速度得到许多学者的认可和使用。

韩建文等[2]通过FLAC3D数值模拟技术对某矿山深部开采的回采进路模拟分析，确定断面4 m×4 m为最佳回采方案。郭进平等[3]等通过FLAC3D数值模拟技术确定既能保证出矿巷道的稳定，又能提高矿石回收率的破碎矿体出矿巷道的最佳间距为12.5 m。陈登红等[4]利用FLAC3D数值模拟技术对深部巷道围岩变形特征进行模拟研究，并与真三轴实验结果和实际测量的结果最对比，揭示了深部回采巷道围岩拉、压分区的产生机制并初步提出可以防止因过度应变软化而引起深部回采巷道围岩大变形的注浆、喷层等措施；王进等[5]通过FLAC3D数值模拟技术根据采场顶板围岩的应力分布和破坏机理对-500 m中段采场的人工矿柱参数进行了优化。苏仲杰等[6]通过FLAC3D数值模拟技术对五龙矿3431B深部运输巷道的变形破坏机理进行研究分析，确定松动圈的范围，确保了巷道的稳定。CAO等[7]、蔡建军等[8]利用FLAC3D数值模拟技术确定了较好的支护技术并优化了支护参数，为矿山巷道的支护工程的研究提供了参考，对实际工程的安全提供了保障。周辉等[9]基于原位监测结果构建的数值模型对深井巷道掘进过程中围岩扰动应力场的演化特征进行了分析，确定围岩应力扰动范围集中在巷道边墙8 m范围内，并通过扰动应力场和开挖扰动区演化特征的对比，验证了两者部分演化特征较为相似。秦万能等[10]运用应变软化模型和摩尔库伦模型进行计算，提出巷道底板采用锚索束注浆加固的治理方案解决了高水平构造应力条件下巷道围岩易失稳的难题。乔卫国等[11]通过FLAC3D对不同支护措施下的巷道围岩数值模拟结果进行定量分析，提出以锚杆、锚索为核心的锚网索喷联合支护方案，应用于实际工程并使巷道的稳定性和整体性得到有效提升。学者们通过巷道围岩的模拟为实际工程提供了巨大帮助，也验证了FLAC3D数值模拟技术的准确性与适用性。

虽然对深部巷道的模拟研究较多，但对于巷道开挖加卸荷诱发围岩破裂失稳的研究却很少，本文以云南某矿山1261中段沿脉巷道为例，通过FLAC3D对深部巷道开挖加卸荷情况下围岩的应力场、位移变化和塑性破坏区演化情况进行模拟研究，其中应力场主要探究巷道围岩在初步开挖后应力重分布情况，及随着开挖进行巷道围岩应力变化情况，进而分析8#矿体巷道开挖加卸荷诱发围岩失稳情况。

1 工程概况

云南某矿山8#矿体赋存于下石炭统摆佐组上部粗晶白云岩中，矿体顶板、底板与围岩界限清楚，沿层产出。矿体产状与地层一致，走向北东20～40°,倾向南东,倾角61～63°。8#矿体在剖面上呈层状一似层状，总体空间形态呈条带状向南西侧伏，矿体水平厚度为2.5～18.8 m，平均水平厚度为9.93 m，矿体沿走向和倾向延伸稳定，仅厚度上存在一些膨胀和收缩。其1261中段沿脉巷道形状为三心拱巷道，该地层厚度为40～60 m，埋深为1 275 m，断面尺寸为3 m×3 m，且在钻探过程中发现有不同程度的岩芯饼化现象，因此需要探究该中段沿脉巷道在开挖过程中的稳定性。

2 深部巷道开挖特性数值模拟

高应力环境下的巷道围岩在开挖过程表现出来的巷道围岩变形特征和浅部差异很大，受地质条件和监测技术的制约，无法准确获取巷道围岩的演化特征，故对1261中段的巷道开挖卸荷过程进行数值模拟，对实际工程提供理论依据与借鉴。

2.1 模型建立

根据圣维南定理及相关文献[12]，巷道局部开挖应力释放引起的岩体扰动的范围大约在巷道中心3～5倍巷道跨度的范围之内，并结合该矿体上向进路机械联合式充填的采矿方法和现场实际状况最终确定巷道模型几何尺寸为25 m×25 m×10 m(宽×高×长)，边界条件为：水平方向对模型四个侧面的水平速度进行固定约束(Vx=0，Vy=0),铅锤方向对模型底板施加固支约束(Vx=Vy=Vz=0)，再通过ANSYS软件建立巷道三维几何模型并导入FLAC3D软件，最终得到巷道三维几何模型图，见图1。本次模拟采用摩尔库伦模型作为运算准则，模型共有60 186个节点，55 460个单元。为了最大程度提高模拟的适应性，根据模拟要求并以实际为基础做出假定：根据田莉梅等[13]研究结果，断层对巷道的影响随着距离的增加，影响程度逐渐减弱，当达到15 m时，断层对巷道围岩变形和稳定性基本没有影响，故在本次模拟中将矿山中断层、微孔隙裂隙、生产用水、生产震动和地下水进行忽略；岩体视为连续的、各向异性的均匀介质；模拟计算为静态开挖计算，不考虑围岩的黏性和蠕变等行为。

根据室内物理力学试验和Mohr-coulomb准则得到室内岩体物理力学参数，考虑到原岩体受到构造活动的影响，需进行折减计算，通过相关文献[14-15]折减公式最终得出模型岩石物理力学参数值见表1。

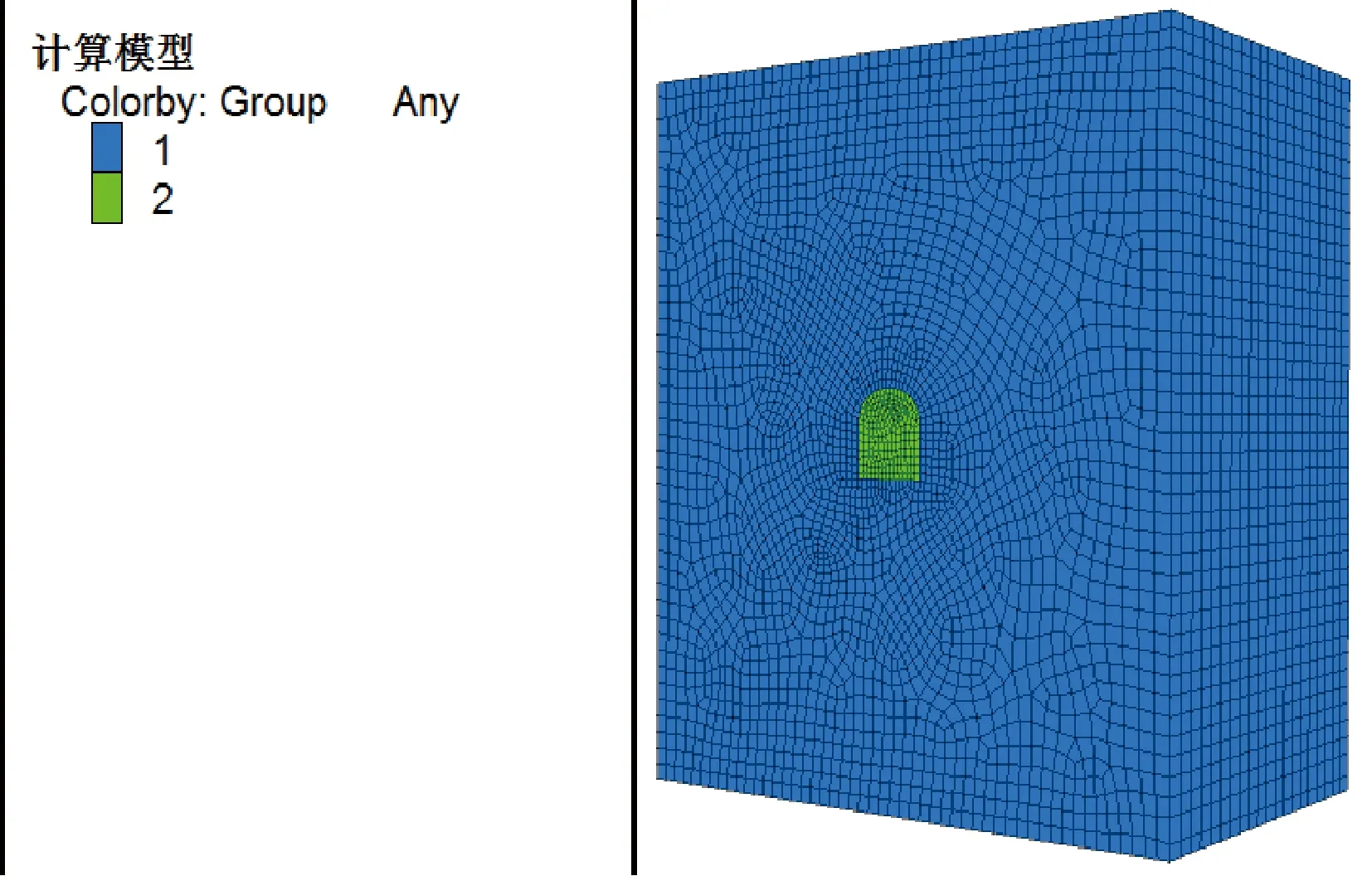
图1 三维计算模型图Fig.1 Three dimensional computation model diagram

表1 岩体模型力学参数Table 1 Mechanical parameters of rock mass model

弹性模量/GPa抗拉强度/MPa黏聚力/MPa内摩擦角/(°)泊松比体积模量/GPa剪切模量/GPa4.302.978.9420.252.871.72

本文采用快速应力边界法，也称S-B法，生成初始应力场。利用AE Kaiser效应得到原岩应力与埋深(>1 000 m)的相互关系[16]见式(1)。

σx=0.029H+1.1

σy=0.022H-1.7

σz=0.022H-2.8

(1)

式中：σx为沿岩层走向的水平应力；σy为沿岩层倾向的水平应力；σz为沿重力方向的垂直应力；H为埋藏深度。

通过计算得到在模型中Z=0时实际埋深1 289 m的水平方向沿岩层走向的初始地应力σx=38.48 MPa，沿岩层倾向的初始地应力σy=26.65 MPa，重力方向的初始应力σZ=25.56 MPa。运用渐变应力公式得出初始应力场不同方向的初始值和梯度值后运用FLAC3D软件计算并得出模型三分方向的初始应力场。

2.2 模拟方案

考虑到巷道模型断面的对称性，只对巷道的一半进行监测。经多次开挖分析计算后发现：巷道内壁向内延伸6 m是巷道发生变形的主要范围，因此监测点都在此范围内布置，主要位置为巷道底板、斜底角、帮部、拱肩、斜拱肩和拱顶，且每个位置的监测线上均布置6个监测点，各监测线相邻监测点间距均为1 m，布置情况见图2。监测点的主要作用是监测并记录开挖过程中应力及位移的变化值，导出并制作应力及位移云图，观察应力和位移的变化情况，进而分析巷道围岩在开挖过程中的变化规律。

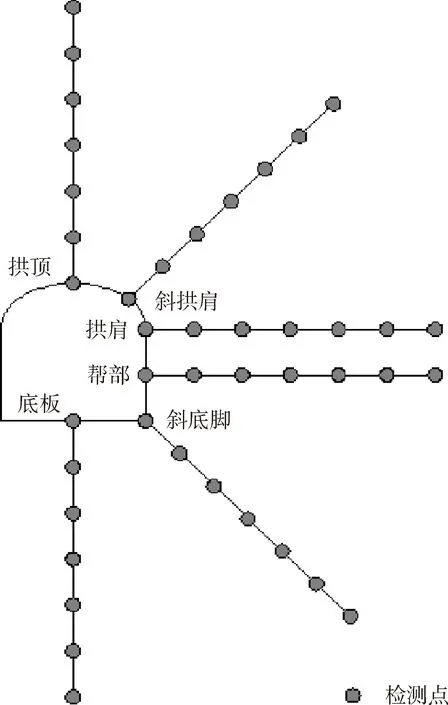
图2 监测点布置图Fig.2 Layout of monitoring points

本次开挖巷道全长10 m，分五步开挖，每步开挖2 m，且均采用无支护开挖。前一步的开挖计算达到平衡后再进行后一步的开挖，直至巷道开挖贯通，巷道开挖一步即2 m时模型计算2 000步。

3 结果与分析

3.1 开挖应力场演化分析

3.1.1 最大主应力演化

利用Kaiser效应得到巷道原始的切向地应力为26.65 MPa，径向地应力为25.56 MPa。由图3可以看出，巷道在初步开挖完成后，巷道各个位置的应力进行了重新调整，巷道围岩帮部切向应力加载到55.4 MPa，径向应力卸荷到15.3 MPa；巷道斜底脚处切向应力加载到64.9 MPa，径向应力卸荷到20.4 MPa；巷道斜拱肩处切向应力加载到63.3 MPa，径向应力卸荷到15.8 MPa。巷道其他位置都有不同程度的应力集中现象。

图3 第一步开挖主应力分布云图Fig.3 Cloud map of principal stress distribution in preliminary excavation

图4 不同开挖步数最大主应力分布云图Fig.4 Distribution of maximum principal stress distribution indifferent excavation step

图4反映了巷道围岩最大应力值随着开挖进行不断变化的情况。其中巷道帮部主应力值随着开挖的进行不断减少，第二步开挖结束后为33.8 MPa，并随着开挖进行依次减少为32.4 MPa、30.6 MPa和29.1 MPa，距离工作面越远，应力值越小；巷道斜底脚处主应力值随着开挖进行逐渐增加，依次为：72.8 MPa、76.3 MPa、77.8 MPa和79.1 MPa；巷道斜拱肩处主应力值随着开挖的进行不断减少，依次为58.5 MPa、57.3 MPa、56.9 MPa和56.2 MPa，距离工作面越远，应力值越小。其他位置的最大主应力值均随着开挖的进行逐渐减少，且距离工作面越远，应力值越小。

3.1.2 偏应力(主应力差)演化

为了更深入地了解开挖加卸荷对围岩稳定性的影响，通过编写fish语言监测巷道各位置的主应力差来综合分析开挖加卸荷对巷道围岩稳定性的影响。图5中“1 m”指距离巷道内壁1 m。

除帮部和底板外，距离巷道壁越近的区域，主应力差值越大，并随着开挖进展主应力差值继续增加。在开挖的初始阶段，各位置应力进行初始加载，并且增长幅度很大，其中斜拱肩主应力差值最大，为47.8 MPa，其次为拱顶的41.3 MPa，拱肩的36.5 MPa，都随着开挖的进行逐渐增加，并在巷道内壁附近达到峰值。

巷道围岩底板和帮部在第一步初始加载完后距离巷道内壁0.5 m左右分别达到峰值为36.2 MPa和34.9 MPa，并在第二步开挖初始阶因瞬间卸荷导致主应力差减小到30.1 MPa和30.2 MPa，并随着开挖的进行趋于平稳。

最小为斜底脚处的27.1 MPa，也是主应力最集中的位置，随后的每一步开挖都会有明显卸荷现象，在巷道内壁附近时的主应力差值明显大于巷道深处的主应力差值并随着开挖进行不断增加。

距离巷道1 m内和1 m外的主应力差值差距明显。而且距离巷道内壁1 m范围内，巷道围岩主应力差值在第一步开挖结束平衡后进行第二步的开挖的初始阶段有着瞬间降低现象，而在1 m范围外，巷道主应力差值在第一步结束，第二步开始阶段主应力差值有瞬间增加的现象。

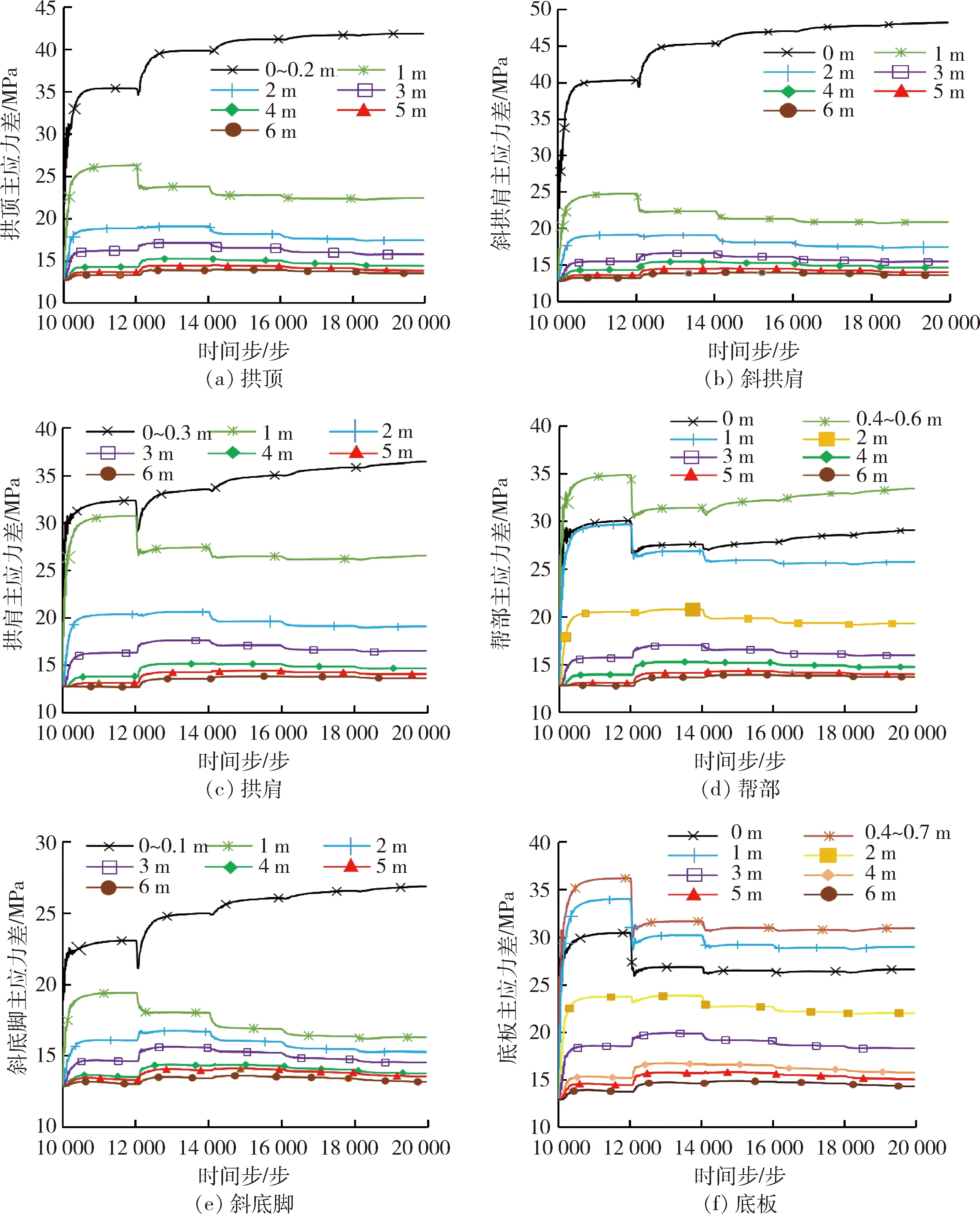
图5 各监测点位置主应力差演化图Fig.5 Evolution diagram of principal stress difference at each monitoring point

3.1.3 岩爆倾向性分析

岩爆是高应力环境下深部巷道开挖过程容易发生的一种地质灾害现象，结合钻探过程中发现有不同程度的岩芯饼化现象，故对巷道开挖过程的岩爆倾向分析是判断巷道稳定性的重要途径。

对于岩爆倾向性的判据有很多，基于本文开挖卸载后原岩应力重新分布使巷道围岩应力承载力所引发的失稳现象这一观点选择谢学斌判据[17]，其表达式见式(2)。

∂=σ1/σc

(2)

式中：σ1为最大主应力；σc为最大抗压强度，其判别准则见表2。

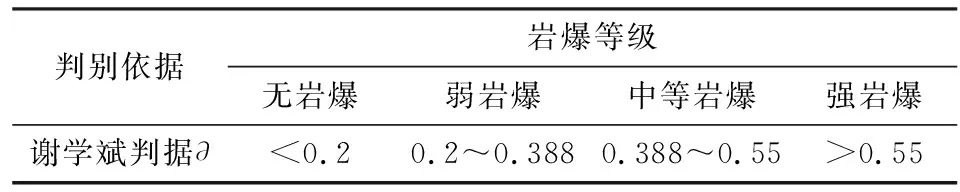
表2 谢学斌岩爆判据表Table 2 XIE Xuebin’s rock burst criterion table

由单轴压缩试验得出岩石最大抗压强度σc为53.39 MPa，根据式(2)得出各测点位置岩爆倾向性评价结果见表3，可知8#矿体岩爆倾向性为中等～强烈岩爆，岩爆可能发生的主要危险区域为开挖断面折角处。

3.2 位移演化

图6为不同开挖步位移变化图，限于篇幅给出第一步和第五步开挖位移变化图。由图6可以看出，巷道围岩在每一步完成后都产生了变形位移和形变量，形变量最大的部分为巷道底板、帮部、拱顶和开挖面，而由于巷道斜底脚位于应力交汇处，应力没用足够的释放空间，岩体因应力集中得到强化，因此巷道斜底脚出岩体处于压密状态，位移量不明显，在第二步开挖过程中达到最大为3.5 mm。整个开挖卸荷过程中围岩竖向位移量最大位置为巷道拱顶和底板，主要因为这两个位置的自由面都垂直于铅垂应力方向，监测点周围围岩在卸荷时产生的变形会较明显，拱顶围岩变形量随着开挖卸荷的进行不断增加，直至开挖完成后达到16.8 mm，底板围岩在前三步开挖进行中不断增加，在第三步开挖过程中竖向位移量达到最大为15.1 mm，随着开挖卸荷的继续进行，底板围岩位移量出现了很小程度的持续减小。巷道帮部围岩的横向位移量是整个巷道最大的，最先遭到破坏并随着开挖的进行从第一步的11.6 mm持续增加到16.7 mm。

表3 各测点位置岩爆倾向评价结果Table 3 Evaluation results of rockburst tendency at different measuring points

3.3 开挖塑性区演化

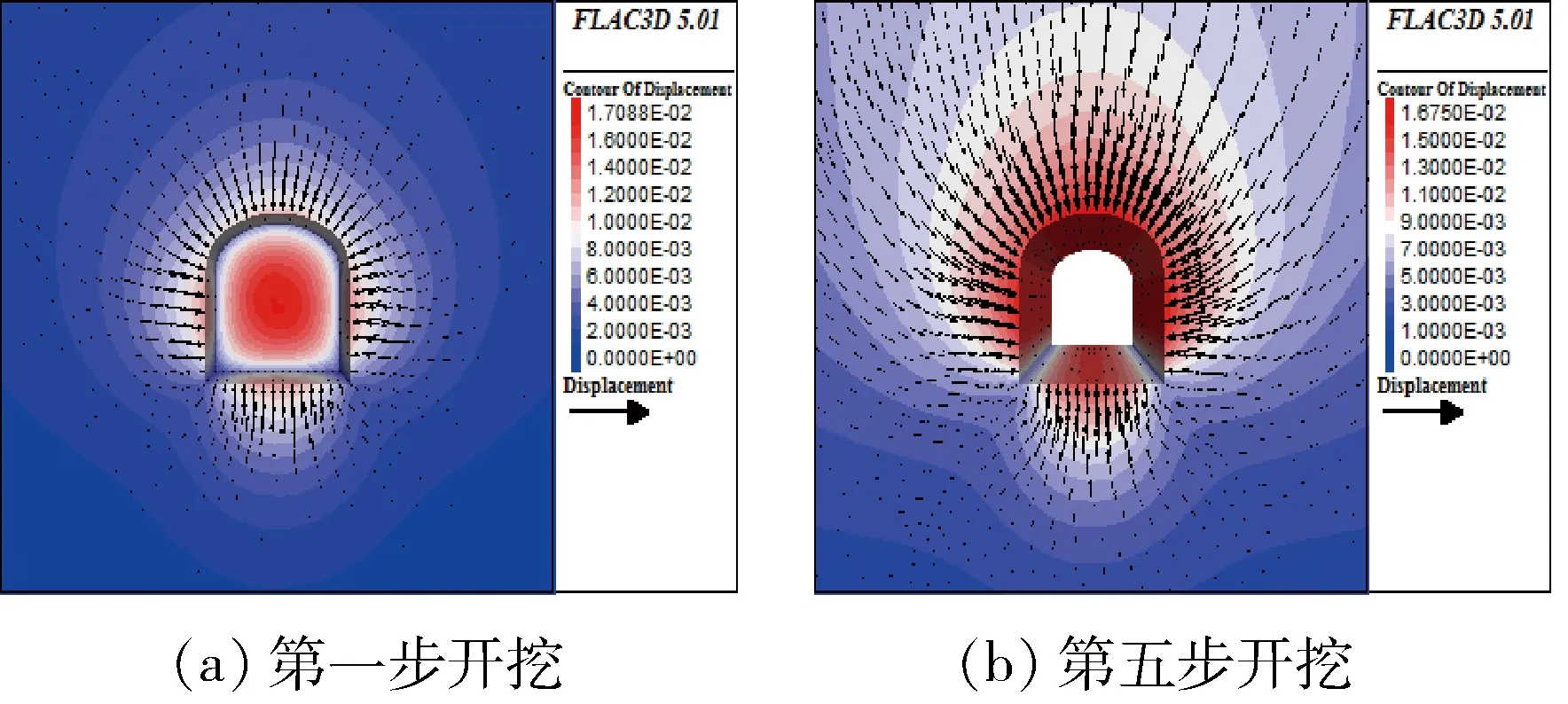
图6 不同开挖步位移演化云图Fig.6 Evolution of different excavation step clouds

图7 巷道开挖围岩塑性区演化图Fig.7 Plastic zone evolution diagram of surrounding rock in roadway excavation

图7为巷道围岩塑性区演化图，限于篇幅给出第一步和第五步开挖塑性区演化图。图例中sh-p、sh-n、ten-p、ten-n分别表示曾发生过剪切破坏、正在发生剪切破坏、曾发生过拉伸破坏和正在发生拉伸破坏。从图7可看出，塑性区主要分布在巷道的四周和开挖面中部，塑性区体积随着开挖的不断进行不断增加。不同形式的塑性破坏交替发生在巷道肩部、拱顶、底板和帮部，但演化图大部分为曾发生过剪切破坏。斜底脚处因应力持续集中并未超过储能极限,未出现塑性破坏区。随着开挖步数的增加，巷道自由面也在增加，围岩塑性区的剪切破坏和拉伸破坏的体积都在不断增加，但正在产生拉伸破坏的围岩体积很小，并随着巷道围岩在每一步开挖结束后的再平衡过程逐渐消失，从演化曲图上看，塑性破坏区主要破坏形式为剪切破坏，伴随少量拉伸破化。

4 结 论

1) 巷道帮部、斜底脚和斜拱肩处切向应力在第一步开挖时加载到最大值，径向应力发生卸荷。随着开挖的继续进行，巷道围岩应力逐渐减小并趋于稳定，巷道围岩多处于临界破坏或破坏状态。

2) 8#矿体沿脉巷道岩爆倾向性为中等～强烈岩爆，巷道折角处危险性较高。

3) 巷道围岩在每一步完成后都产生了不同程度的变形量，变形最大的部分为巷道帮部和拱顶，位于应力交汇处的巷道斜底脚处的岩石在达到极限储能前会继续储能，位移量较少。

4) 塑性区主要分布在巷道周围，在第一次开挖时出现大面积塑性区并随着开挖进行逐渐增大，塑性破坏区的破坏形式主要为剪切破坏并伴随少量拉伸破坏。