MIKE模型在长江下游河段涉河工程洪水影响分析中的应用

曾慧俊

(安徽省长江河道管理局,安徽 芜湖 241000)

随着数值模拟技术的发展,许多计算软件在中国的河流模型计算中广泛应用[1-3]。其中由丹麦开发的MIKE21软件可以用于模拟各种作用力下河道水位及流速的变化。河道中涉河工程的建设势必将改变河道过流条件,进而影响局部流场,利用MIKE模型对工程建设前后水位流速变化进行计算分析,为评价涉河工程对河道行洪能力的影响提供数据支撑。

1 河道概况

黑沙洲河段与芜裕河段均属芜湖市管辖。其中黑沙洲河段上起繁昌县荻港与铜陵河段相接,下至三山河口与芜裕河段上段相连,为首尾束窄、中间展宽的典型鹅头分汊河段。分汊段内有天然洲、黑沙洲,分水流为左、中、右三汊,高水位时,右汊微弯、中汊顺直、左汊弯曲。芜裕河段上段平面形态呈微弯“∽”型,江中潜洲将水流分为左右两汊,左汊为主汊。从高安圩至头棚为上弯段,深槽傍右岸,左岸是大套沟边滩；过头棚后深槽摆向左岸进入下弯段,在三坝以下深槽贴左岸下延至大拐,而右岸是大白茆边滩。该段右岸高安圩—保定圩、左岸三坝—大拐为水流贴岸区(图1)。

本次涉河工程为一高桩梁板码头,位于长江黑沙洲河段出口汇流段右岸。

2 模型建立

2.1 计算原理

平面二维水流数学模型的基本方程包括连续性方程和动量方程,在笛卡尔坐标系下的控制方程形式如下。

连续性方程为:

(1)

x向和y向运动方程为:

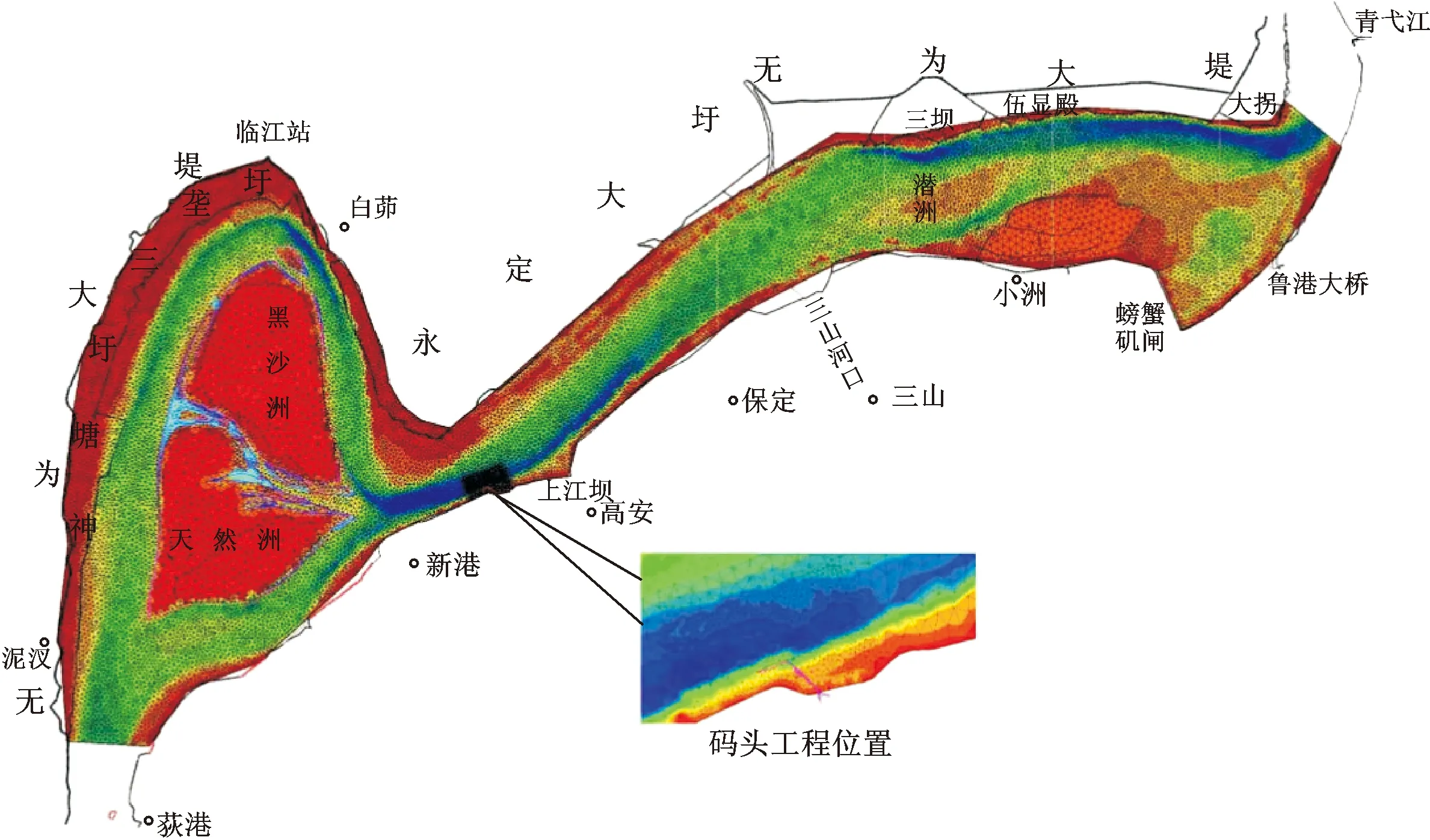
图2 计算区域网格划分Fig.2 Mesh generation of computation area

图3 验证流场图Fig.3 Verification of flow field diagram

(2)

(3)

式中:t为时间；x、y为笛卡尔坐标的两坐标轴；η为水面高程；d为水深；h=η+d为总水深；u、v为对应于x、y的速度分量；f=2Ωsinφ为科氏力(φ为纬度)；g为重力加速度；ρ为密度；ρ0为相对密度；vt为涡粘系数；Pa为大气压强；S为源汇项的流量(us、vs为源汇项对应的速度分量)。

在二维的水动力模块中流速是一个平均的概念:

(4)

2.2 计算网格

计算区域内地形比较复杂,为了合理布置计算网格,本文采用Delaunay三角化法对计算区域进行网格划分,并在工程位置附近进行了加密。在计算区域内共布置了17 945个网格节点和34 882个计算单元,其中工程附近计算网格间距约为20 m。工程河段的网格布置图见图2。

2.3 参数设置与模型验证

采用2007年6月洪水季实测水文资料与2017年3月枯水季水文资料进行厘定与验证。模型按曼宁公式计算断面平均糙率,作为初始计算的糙率值。考虑到糙率随水深具有深水区比浅水区糙率小的变化趋势,模型计算中用节点水深对断面平均糙率进行修正,再根据水位、流场情况对糙率系数进行分段调试。本河段糙率取值范围为主槽0.017～0.020 ,滩地0.022～0.028。

模型对2017年3月(Q=16 700 m3/s)实测的黑沙洲左右汊分流比、固定断面水位及流速进行了验证,验证流场、流速及潮位见图3-图5。

以上表明,经调试后的模型计算结果与实测数据吻合较好,其最大误差不超过2%,精度达到评价计算要求。

2.4 建设项目概化

建设项目为一座高桩梁板式码头,码头平台长112 m、宽20 m,平台下部采用钢管桩基础；码头接岸引桥总长约244.4 m,引桥标准排架间距为16 m,基础采用Φ800PHC管桩和Φ800钻孔灌注桩。

涉河工程对河道的影响主要体现为两方面:一是工程施工改变了原过流滩地地形;二是建筑物构造增加了水流阻力。为了反映建设项目对河道地形的改变,在模型计算中采用以下两种方法:一是对局部地形进行修正,将工程施工后的地形高程点纳入到模型计算地形中；二是通过计算现有桩基础减小的拖曳力来反映码头桩基础对水流的阻力,每个桩基础上减小的拖曳力在MIKE21中通过动量公式转化为切应力来计算,即:

τp·Δx·Δy=n·F

(5)

式中:τp为切应力;F为桩基础上的拖曳力;n为每个计算网格上桩基础个数(即分布密度);Δx、Δy为计算

图4 典型断面流速验证Fig.4 Verification of flow velocity in typical section

图5 典型断面潮位验证Fig.5 Verification of tidal level in typical sections

网格边长。拖曳力F由以下公式来计算:

F=1/2·ρCDBeHe·V2

(6)

式中:CD为拖曳力系数;ρ为水密度;Be为柱体的影响宽度;He为桩基础阻水长度;V为水流流速。

3 不同洪水组合下建设项目对河道行洪能力的影响

为分析工程修建后对长江行洪的影响,计算方案主要考虑长江汛期高水位条件,同时也兼顾中水位下工程前后水位、流场变化。选择长江下游防洪设计水位对应的设计洪水流量(Q=92 600 m3/s)、1998年洪水流量(Q=82 300 m3/s),及平滩流量(Q=45 000 m3/s)作为本次计算的洪水条件(表1、表2)。

分析计算结果,通过工程建设前后局部河道水位变化图(图6)可以看出,码头项目建成后,工程局部区域内水位变化主要体现为码头平台上游水位壅高,码头平台下游水位降低。三种工况下设计洪水流量影响范围与极值均大于后两种工况,水位最大增加0.9 cm,最大降低1.3 cm,水位变化值>0.2 cm的范围为码头平台上游150 m至平台下游660 m。通过工程建设前后局部河道流速变化图(图7)可以看出,码头平台的建设压缩了河道过流断面,主要表现为码头平台上下游流速减小,外侧局部区域流速增大。在设计洪水流量下,流速最大增加值为0.08 m/s,最大减小值为0.21 m/s。

表1 工程前后水位变化表Table 1 Water level change table before and after construction

表2 工程前后流速变化表Table 2 Variation table of flow velocity before and after construction

在设计洪水流量条件下,天然洲被水淹没,此处只考虑1998年洪水流量和平滩流量条件下码头工程对天然洲分流比的影响。表3给出了1998年洪水流量及平滩流量条件下天然洲右汊分流比的变化,由表3可知,码头项目的实施将导致天然洲右汊分流比的减少,但减小值很小。

表3 工程实施前后天然洲右汊分流比Table 3 The diversion ratio of the right branch of natural continents before and after the implementation of the project

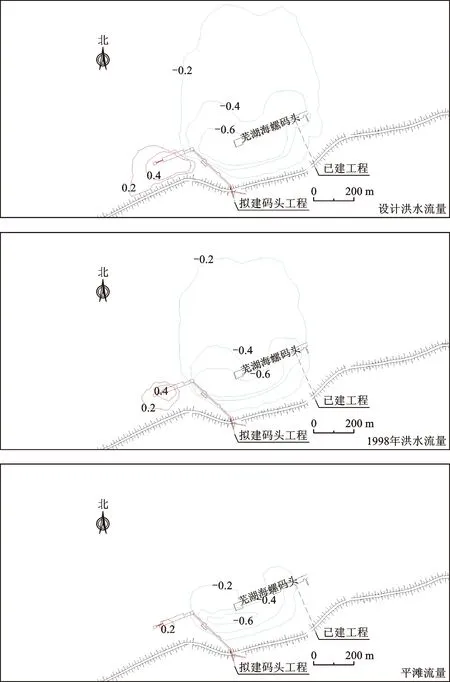
图6 不同工况下局部水位变化Fig.6 Local water level change under different conditions

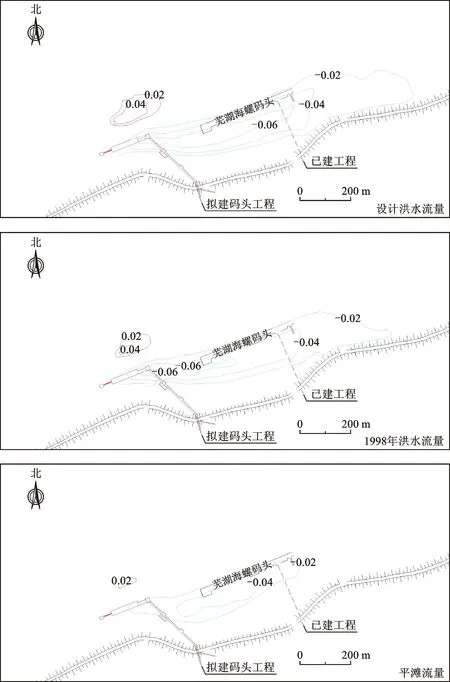
图7 不同工况下局部流速变化Fig.7 Local velocity variation under different working conditions

4 结语

本文基于MIKE模型,计算分析了某码头项目的建设对长江下游芜湖河段河道行洪能力的影响。通过研究计算过程与分析计算结果,结论如下:

(1) MIKE模型计算结果与实测水文资料吻合较好,精度满足洪水评价要求,能反映出本河段的水流运动特性。

(2) 模型采用局部地形高程修正与码头桩基础拖曳力减小两种概化方法,可以较好地模拟出码头类工程建设前后对局部流场的影响。

(3) 码头项目建设对河道局部水位及流场的影响较小,对主流位置及汊道分流比影响较小,不会对河势产生明显不利影响。