球坐标系下多介质混合物模型的数值模拟*

吴宗铎，赵 勇，严 谨，宗 智，高 云

（1.广东海洋大学海洋工程学院，广东 湛江 524088；2.大连海事大学交通运输工程博士后流动站，辽宁 大连 116026；3.大连理工大学船舶工程学院，辽宁 大连 116024；4.西南石油大学油气藏地质及开发工程国际重点实验室，四川 成都 610500）

多介质的激波间断问题一直以来都是计算流体力学方面的一个备受关注的问题，目前广泛应用的一个处理方法是利用Level Set 函数追踪气水界面，同时结合近似Riemann 解下的虚拟流体质点完成对冲击波参数的计算[1]。虽然得到的结果较理想，但是计算过程复杂，且计算依赖近似Riemann 解，无法在JWL (Jones-Wilkins-Lee)及Mie-Grüneisen 等复杂形式状态方程下展开更深入的研究[2-3]。

相比之下，利用多介质混合模型，可以将流场视为一个整体并用体积分数或质量分数来区分流体，从而在不直接求近似Riemann 解的前提下完成计算。多介质混合物模型早期由Abgrall 提出[4-5]，通过非守恒方程来计算由气体或低压缩度的固液体组成的流场[5-6]。随后，Abgrall 将该混合物模型扩展成一个七方程模型，能适应一般形式状态方程的流场[7]。柏劲松等[8]也利用此类多介质混合物方程来模拟两种以上介质的冲击过程，且配合等效方程可以适应一些复杂形式的状态方程[9]。梁珊等[10]和Liang 等[11]将Abgrall 的七方程模型与多GPU 的并行计算相结合来提高计算精确度。为了让算法更好的适应并行计算，刘娜等[12]将谱体积方法运用到多介质混合物模型中，提升了计算效率。

虽然该多介质混合物模型在采用直角坐标系处理平面波的问题时，取得不错的进展，但是对于常用于处理球面波的球坐标系下的多介质问题，仍然具备一定的局限性。第一，多介质混合物模型建立在速度和压力在界面处维持平衡的基础，仅对平面波适用，但是球面波的压力和速度都会随着传播半径的增加而衰减；第二，球坐标系下，原点位置处为冲击波运动的奇点位置，必须作出合适的处理；第三，为了增加工程实用性，计算模型需要能适应复杂形式的状态方程，而不仅仅是理想气体方程等形式简单的状态方程。

考虑到以上因素，本文将直角坐标系下的基于Mie-Grüneisen 状态方程下的多介质混合模型延伸到球坐标系下。为了压力和速度不平衡问题以及坐标原点的奇点问题，在原计算模型下作了参数修正并用质量分数替换体积分数，并对奇点处数值差分作了特殊处理—利用相邻网格点参数赋值给奇点参数但奇点处速度设定为0。最后，将通过数值算例验证其数值稳定性和计算准确性。

1 直角坐标系下的计算模型

考虑多介质的可压缩流体组成的混合流场，其运动形式可以用欧拉方程来描述：

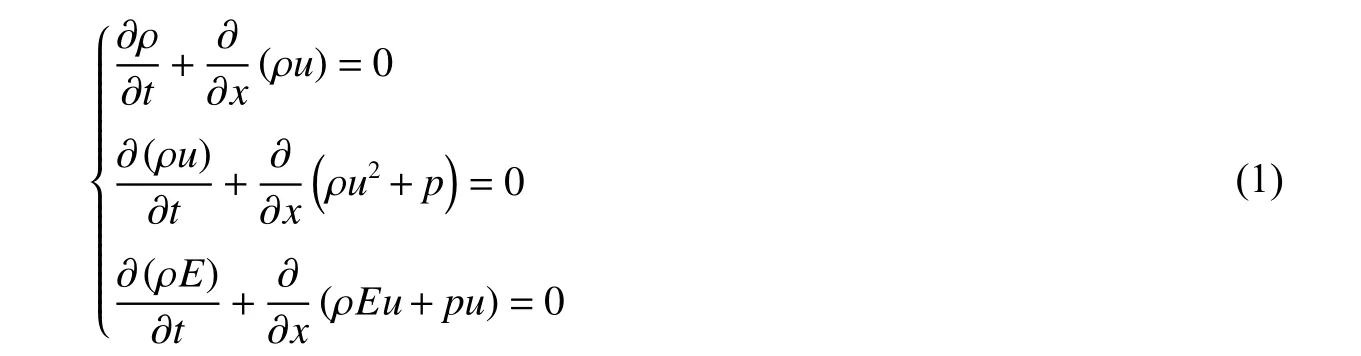
式中：ρ、p、u、E 分别为密度、压力、速度和单位质量能量[13]。单位质量的总能量为内能和动能的总和，且E=e+u2/2。

流场中介质的物理特性，可以用Mie-Grüneisen 状态方程来表述：式中：Γ 为Mie-Grüneisen 系数，pref和eref为参考点的压力和单位质量内能，与密度ρ 有关。

1.1 界面处热力学关系

界面处，流体的压力p 和速度u 均保持平衡[4]，此时p 与u 在界面处不发生变化，而密度ρ 与内能e 则出现数值间断。因此∂p/∂x 和∂u/∂x 约为0，式(1)中的质量守恒与能量守恒可以分别表示为：

将式(2)代入式(4)，有：

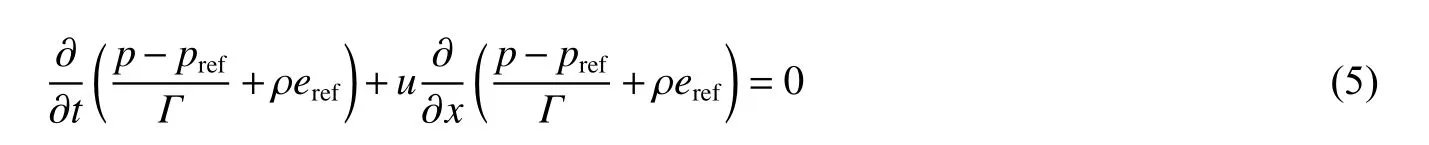
由于Γ、pref、eref都只和密度ρ 有关的函数，且式(5)对于任意的表达式pref(ρ)和eref(ρ)均成立。这里首先假设pref、eref都为0，那么有[2,9]

同理，可依次类推得到关于pref和eref的非守恒形式的方程：

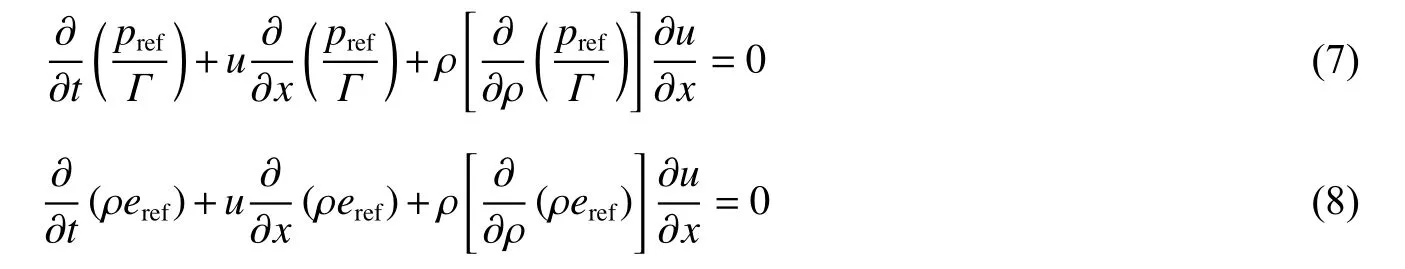
1.2 波面处热力学关系

由于式(6)～(8)的推导过程需要基于p 和u 在界面处连续这一前提条件，但是在左右波面处，p 和u 均出现间断面，式(3)和(4)不再成立。此时，对(6)作如下考虑：

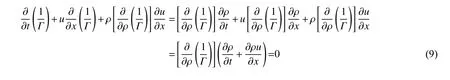
因此，在左右波面处虽然p 和u 均间断，但由于在同类介质中1/Γ 等参数的导数保持连续，因此，式(6)依然成立。同理，式(7)和(8)在左右波面处也成立。

1.3 输送方程

对于多介质流场，必须利用输送方程来捕捉界面的运动。流场中，某种介质的界面随时间变化的运动方程，称为输送方程。一般利用体积分数zi来建立介质的输送方程：

式中：i 为介质的种类序号。非守恒变量1/Γ、pref/Γ、ρeref均为独立变量，但它们对的ρ 偏导数可表达成关于体积分数zi的加权叠加。这样，综合式(1)、(6)～(8)和(10)，可完成直角坐标系下的多介质流场的求解。

2 球坐标系下的计算模型

球坐标系下，则需要考虑更多的问题。

第一，在采用直角坐标系下计算平面波问题时，p 与u 在界面处维持不变且偏导数∂p/∂x 与∂u/∂x 基本为0。该数值特性一直从界面处向左右延伸，直到波面处才形成间断，如图1 所示。但是采用球坐标系处理球面波问题时，当冲击波沿着半径r 向外扩散时，传播的形式则不再是平面冲击波，而是球面冲击波。此时，虽然p 与u 依然在界面处连续，但是球面波的扩散过程中p 与u 会随着半径增加而发生衰减，并非保持不变。因此，球面冲击波在界面处的偏导数∂p/∂r 与∂u/∂r 不再是0，而是一个稳定的负数。这种情况下，式(3)～(4)非守恒性方程的建立的理论基础并不十分准确。

第二，球坐标系下的内外介质产生相互作用时，内部的稀疏波(或激波)汇聚到一起后又反向朝着外部扩散，原点处便形成了一个奇点。奇点处的稀疏波形成了独特的反射机制。因此奇点的物理参数变化需仔细考虑。

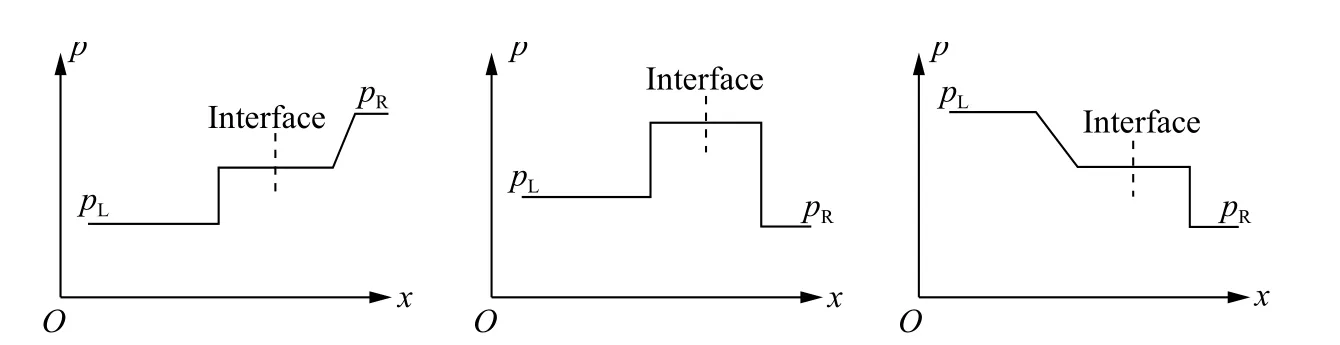
图 1 平面冲击波界面处p 的数值特征Fig.1 The numerical property of p at the interfacefor plane shock wave

2.1 球坐标系下控制方程

这里将球坐标系下的控制方程表示成守恒变量U 与通量F 的关系为[13-14]:

其中：

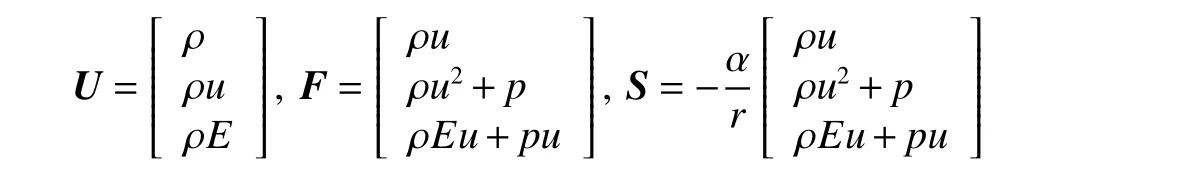
式中：系数α=2。式(11)可以改写成：

其中：

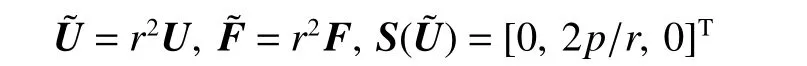
此时，将非守恒形式的方程组添加到式(11)中，即可得到球坐标系下的控制方程。

2.2 热力学参数修正

需要注意的是，非守恒形式的方程式(6)～(8)的推导，是以界面处于平衡状态为前提的。在球坐标系下，由于冲击波是沿着球面向四周扩散。随着扩散范围的增加，几乎所有的冲击波参数都会随着半径增加而降低。此时，p 与u 在界面处将呈现出持续的减小趋势。这样，式(6)～(8)无法直接使用到式(12)中。在直角坐标系和球坐标系下，界面间断的关系分别为

考虑到三个非守恒变量1/Γ、pref/Γ、ρeref均为密度ρ 的函数，这里每隔一个时间步对它们做修正:

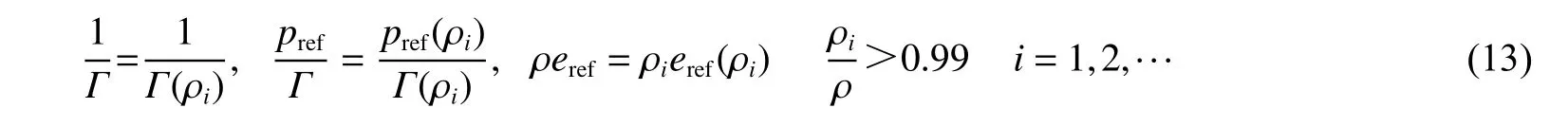
式中：ρi为介质i 的密度。而的其他参数如ρ、p、u、E 的计算，仍然借助当前时间步下的Γ、pref、eref。而式(6)～(8)则保留在系统方程中，并且每隔一个时间步，非守恒变量1/Γ、pref/Γ、ρeref都会得到修正。当时间步足够密时，非守恒形式在球坐标系下带来的误差可以控制在一定的范围内。

2.3 输送方程变换

由于每隔一个时间步，都会需要利用ρi进行修正。这里用质量分数代替体积分数来构造输送方程。利用式(12)中的质量守恒关系可得：

根据式(14)得到的质量分数yi可以很容易得到各介质的密度ρi(i=1, 2, ···)。而非守恒方程(6)～(8)中的偏导数，则转换成与质量分数相关的加权叠加：

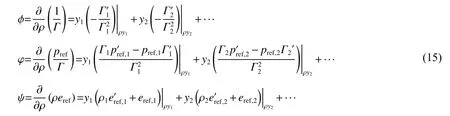
式中：φ、φ、ψ 为非守恒变量1/Γ、pref/Γ、ρeref偏导数，下角标1、2 代表流场中介质的序号。

相比式(10)给出的基于体积分数的输送方程，基于质量分数的输送方程能考虑到每一种介质的密度ρi，从而得到更为合理的偏导数φ、φ、ψ。

2.4 奇点处理

对于球坐标系来说，奇点是一个无法避免的问题。参考文献[15]中对奇点的处理方式，奇点处质点的运动速度为0，即u=0，但是奇点处的质量和能量守恒关系依然成立：

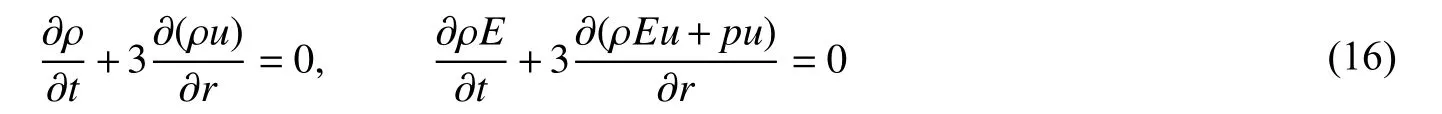
展开后，将u=0 代入，有：

由于在奇点处主要涉及冲击波的汇聚和发散，不涉及界面的运动，因此，可不考虑输送方程。参数Γ、pref、eref由密度ρ 直接计算得到。

文献[15]中，对偏导数∂u/∂r 采用了如下的计算方式：

式中：下角标1 和2 代表网格点序号。但考虑到本文的方程体系非守恒性较强，将u1和u2都替换为奇点处的速度0，这样偏导数∂u/∂r=0。再根据式(17)计算得到奇点处的其他参数。

2.5 差分格式

在有限体积差分下，第j 个网格点的变量Uj，可按如下格式计算：

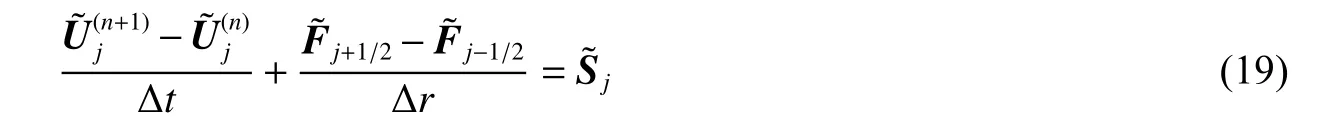
式中：Δt 和Δr 分别为时间和空间步长，上标(n)代表第n 步时间序号。对于物理量第j 和j+1 个网格点之间的通量和 源项分别为：

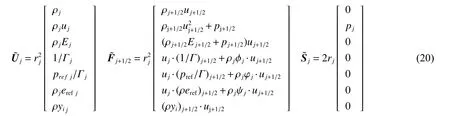
式中：角标j+1/2 表示通量中的参数，角标j 表示网格点的参数；在球面冲击波中，通量表示沿半径r 方向通过j 点的物理变量。

2.6 时间空间步长

时间步长Δt，满足收敛的条件为：

式中：CCFL是为了保证迎风型计算格式收敛而设置的一个0～1 之间的系数，满足收敛的条件为CCFL＜1,并且当CCFL取得越小时间步长越小，计算越精细, 这里取CCFL=0.4； uj和cj表示第j 个网格点的质点速度和声速。声速cj的表达式为：

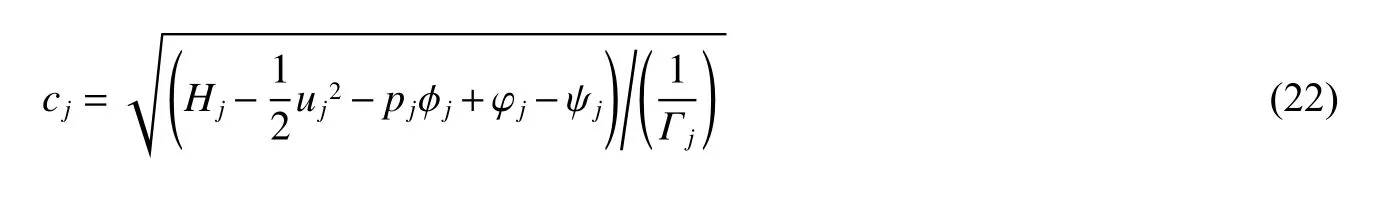
式中：H=E+p/ρ。

3 计算结果

3.1 无因次参数的气水作用算例

这里考虑一个无因次的气水作用问题[16]。初始时刻，中心气团的物理状态为：p=8.3×103，ρ=1.27，u=0，外部水的物理状态为：p=1.0，ρ=1.27，u=0。气体和水的状态方程分别为

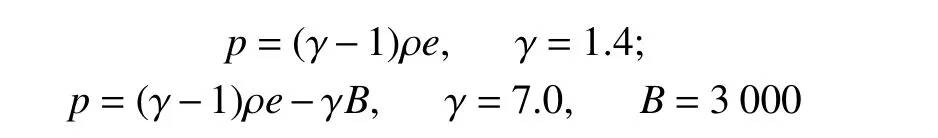
式中：γ 和B 为描述水和气体在低压缩度时的热力学参数。气团初始半径为R0。由于中心气团的压力和密度高于周边水的。因此，高压的气团会在水中形成冲击波并推动界面向外部扩散。对冲击波波面和介质界面的运动位置的变化情况进行记录（波面为水中压力的最大值位置，界面位置为从外向内气体的质量分数刚超过0.5 的位置），并绘制了冲击波和界面随时间变化的曲线，如图2 所示。从图2 可以看出，本文所得到的冲击波和界面的运动位置与Liu 等[16]和Flores 等[17]的结果都比较接近。三个数据的计算结果，在气水作用的初期差别不大。但是随着冲击波和界面向外扩散，本文的计算结果与Flores 等[17]的计算结果相比，误差略偏大，但仍然在一个合理范围内。

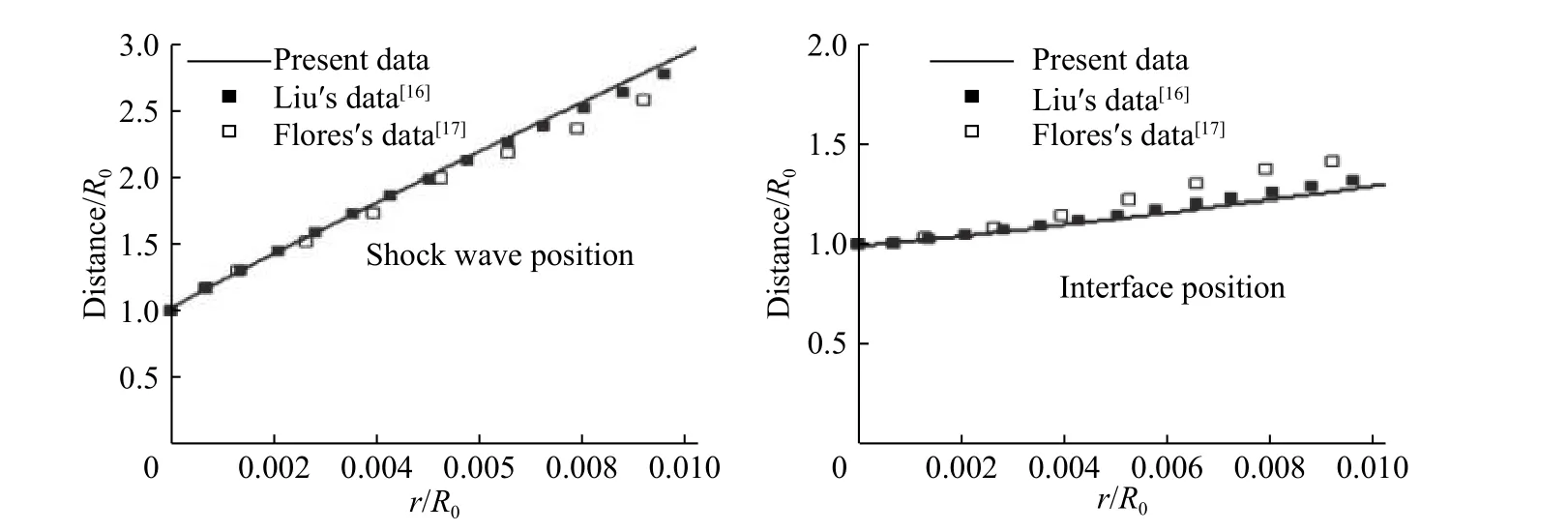
图 2 冲击波与界面位置随时间的变化Fig.2 Time evolutions of position of shock wave and interface

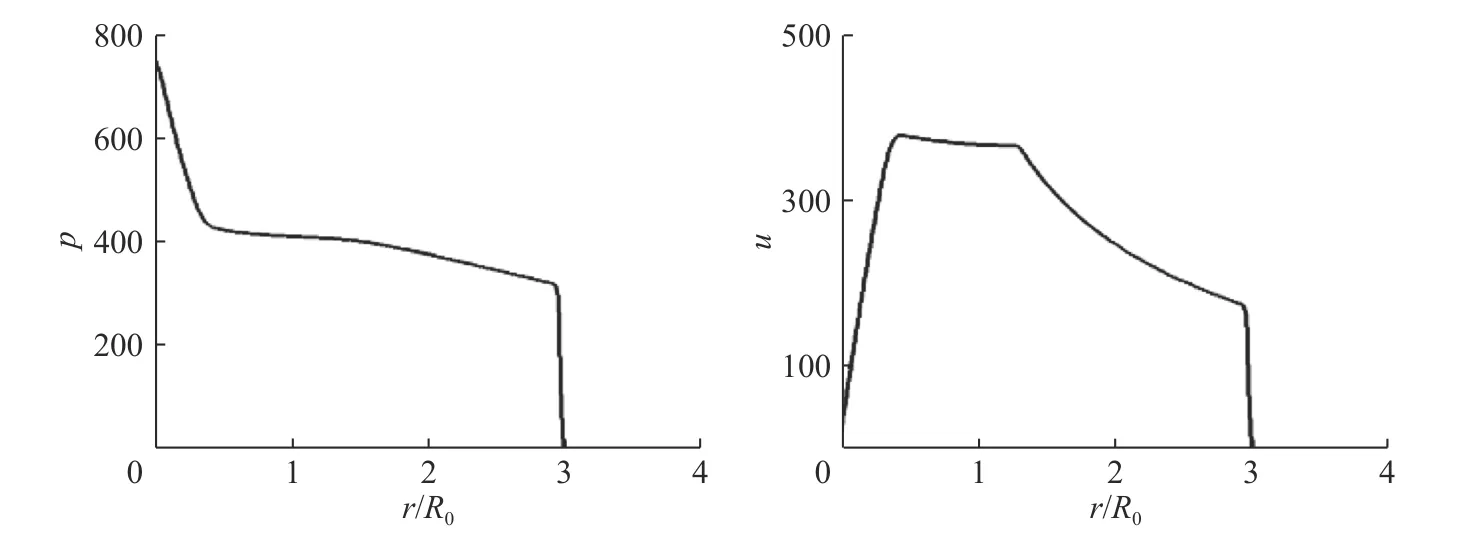
图 3 冲击波到达3 倍R0 时，压力与速度的分布Fig.3 The distributions of pressure and velocity when shock wave reaches 3R0

图3 为冲击波到达3 倍气团初始半径时候的压力和速度曲线。此时，向内收缩的稀疏波已达到中心原点处。由于气团已扩散开，中心处的压力开始逐渐下降，但中心处的速度仍然为0。速度曲线中，由中心向外的第一个拐点为稀疏波的端点，第二个拐点则为界面所在位置。另外，从图3 中可以看出，处于数值奇点的原点处，数值稳定性较好。证明本文所用的奇点处理方式能效果良好。

3.2 圆形药球的水下爆炸算例

假设一TNT 的实心药球质量为50 kg，将空间步长取为炸药球半径的1/100。利用改进后的多介质混合模型计算球坐标系下的冲击波运动情况。

炸药的状态方程为JWL 状态方程[3]：

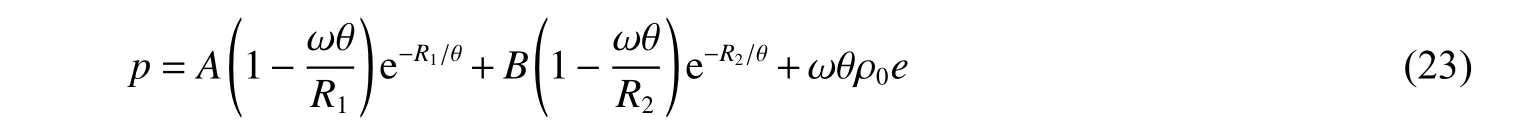
式中：A、B、R1、R2、ω 均为常数，由圆筒试验标定得到[3]；θ=ρ/ρ0，ρ0为物质的初始密度。水的多项式状态方程为[18]：

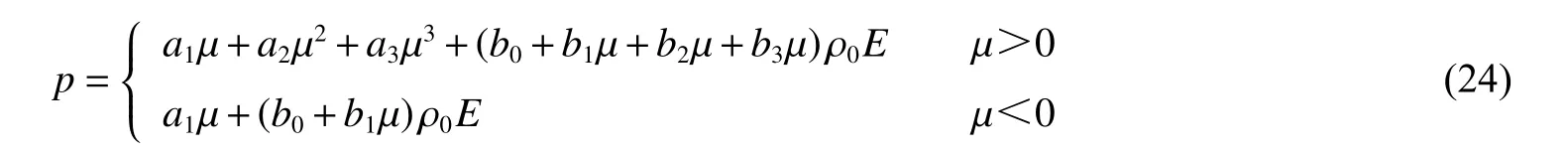
式中：μ=θ-1；a1～a3, b0～b3为展开后的多项式系数。状态方程(23)～(24)的参数取值见表1[19]。

表 1 状态方程参数Table 1 Coefficients of EOS

本算例中，将计算范围扩大至20 倍以上的药球半径。这样，可以得到冲击波运动到不同位置处的压力，如图4 所示。从图4 可以看出，由于在偏导数φ、φ、ψ 的处理方式差异，两种计算模型得到的压力分布有差别。但都具备较好的数值稳定性。当冲击波运动到较远位置时，会出现多个压力峰值。

在实际工程中，最受重视的是第一次的峰值。图5 为冲击波峰值压力随运动距离变化的曲线。作为对比，将给初始的体积分数模型[2]和改进后的质量分数模型同Zamyshlyayev 的经验公式[20]曲线作了对比。对比发现，改进后的质量分数模型可以得到更为准确的计算结果。在压力随运动距离发生急剧下降的过程中，利用体积分数得到的计算结果，得到的结果比经验公式的结果略微偏大。

图 4 冲击波到达不同位置处的压力曲线Fig.4 Pressure curves at the time instants when the shock wave reaches different positions

图 5 冲击波在不同位置处的压力峰值变化Fig.5 Peak value variation of pressure of the shock wave at different positions

图6 为利用体积分数与质量分数计算模型分别得到的压力时程曲线。从不同的计算结果中可以看出，利用改进后的质量分数模型，得到的计算结果好于体积分数模型。各个半径处的压力时程，质量分数模型均吻合得比较好。由于Zamyshlyayev 的经验公式仅考虑冲击波压力最大峰值未考虑压力的二次峰值，本文也仅模拟了冲击波压力的最大峰值。

图 6 不同计算模型下压力随时间变化曲线Fig.6 Time evolutions of pressure for different numerical models

4 结 语

针对球坐标下多介质界面捕捉困难的问题，本文对原始的Mie-Grüneisen 多介质混合物模型作了热力学参数修正、输送方程变换、特殊奇点处理等多项数值改进。改进后的基于质量分数的模型，可以在常规状态方程下准确捕捉界面和冲击波的运动，且可以在适应JWL 等形式复杂的状态方程。而适当的奇点处理也保证了数值计算在奇点处的稳定性。另外，数值算例证明，相比原始的体积分数模型，改进后的质量分数模型可以得到较为准确的计算结果。