外爆条件下冲击波与组合壳结构的相互作用*
高康华,李 斌,刘宇都,孙 松
(1.解放军92656 部队,海南 三亚 572000;2.陆军工程大学爆炸冲击防灾减灾国家重点实验室,江苏 南京 210007;3.南京理工大学化工学院,江苏 南京 210094)
安全壳是核反应堆抵抗外部袭击的最后一道屏障,一旦破坏势必造成放射性物质泄漏、大规模爆炸等严重后果。当前这方面的研究主要集中在弹体侵彻或飞机撞击对安全壳结构的局部贯穿、爆炸破坏作用[1-4],以及安全壳内部炸药或气体聚集引发的事故性内爆炸等[5-8]方面。对常规武器、炸药在安全壳外部一定距离处爆炸,由于安全壳本身尺寸较大,模型实验中爆炸荷载缩比很难实现,通过相似材料制作安全壳模型也极其困难,目前多以简化计算和数值模拟为主:Pandey 等[9]研究了外部爆炸时钢筋混凝土安全壳的非线性响应;余爱萍等[10-11]采用时域边界积分方程,提出半球型安全壳在爆炸冲击波作用下动力响应简化计算模型,考虑了空中爆炸和地面爆炸2 种情况下壳体位移和变形过程;王天运等[12-16]讨论了质点杆模型在冲击波作用下安全壳结构动力计算中的应用,采用流固耦合算法和有限体积元法,对爆炸条件下核安全壳动力响应进行数值模拟,得到安全壳破损的最小安全距离和爆炸当量,评估了安全壳筒墙的抗爆性能,并分析了爆炸地冲击作用下安全壳结构的可能破坏形式;申祖武等[17]将装药爆炸、土中传播和结构构成有限元体系,分析了炸药触地爆条件下安全壳基底的振动响应。
本文中,以核安全壳遭受外部冲击波作用为背景,根据安全壳结构特点,制作带防护墙的地面直立钢筋混凝土组合壳结构,体现了穹顶、环形梁、圆形柱壳和外部防护墙体等几何特征,对细部构造适当简化。鉴于核安全壳爆炸模型实验的复杂性,开展爆炸实验,目的在于研究空气冲击波作用下,此类组合壳外表面荷载和结构振动。由于未考虑相似率,所得实验结论不能直接用于实际核反应安全壳结构的爆炸防护,但相关实验数据可用作对理论计算模型验证和数值模拟方法修正,为核安全壳及同类结构的抗爆安全设计、爆炸作用下的毁伤预测和结构的防护加固提供理论参考和技术支持。
1 实验方法
1.1 模型结构
图1 给出了结构详图,图1(a)~(b)显示模型由穹顶、圆柱壳、防护墙以及底板组成,其中穹顶与圆柱壳通过环形梁连接,确保刚性连接。防护墙顶盖、墙体、层间板、圆柱壳和穹顶厚度均为50 mm,圆柱壳与防护墙间距15 mm,内外防护墙间距150 mm。图1(c)、(d)分别为水平剖面图A-A 和B-B,图中最外边的矩形框是支承底板,通过四周螺栓将整体结构与地面固定,确保刚性连接。中间矩形框是外防护墙,最里边是内防护墙,2 个同心圆是组合壳体拱顶的投影。防护墙是整体的双层结构,在剖面上呈十字形(图1(b))。实验结构采用加钢筋网的水泥砂浆浇注制作,水泥砂浆抗压强度σcon=30 MPa,弹性模量Econ=30.8 GPa;内部采用双向双层退火钢筋网片,钢筋直径d=4 mm,抗拉强度σsteel=215 MPa,弹性模量Esteel=200 GPa,其中组合壳配筋率为1.4%,防护墙顶板、墙体和层间隔板配筋率为0.65%。

图 1 实验结构详图 (单位:mm)Fig.1 Structure detail drawing (unit in mm)
1.2 实验工况
实验分2 种工况,如图2 所示:工况1,将模型结构置于地面;工况2,在结构四周堆围高1.0 m、宽0.85 m 的砂土。2 种工况下,均在距结构一定距离处用高能含铝炸药爆炸加载,爆源形式如图3 所示。
实验中主要量测压力、加速度、应变等参数,结构制作时预留传感器的安装位置。下面详细给出按工况1 实验时结构各类传感器布置图。按工况2 实验时,首先将模型结构周围0.85 m 处围护高度为1 m的沙袋,然后在沙袋与结构之间填入砂土并层层压实,各类传感器布置参照工况1。
1.3 传感器布设
结构外表面爆炸压力量测时,取一半结构布设压力传感器,选取PCB-113B 型压力传感器,其量程为1.38~6.89 MPa,其灵敏度为0.73 μV/Pa,测点分布及编号如图4 所示。
防护墙、圆柱壳及穹顶部位加速度量测时,选取型号为CA-YD-103 的加速度传感器,量程为1 960 m/s2,灵敏度为2.04 pC/(m·s-2),测点分布及编号如图5 所示。

图 2 模型结构爆炸加载实验图Fig.2 Model structures under explosion loadings

图 3 爆源形式Fig.3 Explosion source

图 4 压力传感器的分布 (单位:mm)Fig.4 Distribution diagrams of pressure sensors (unit in mm)

图 5 加速度传感器的分布图 (单位:mm)Fig.5 Distribution diagrams of acceleration sensors (unit in mm)
防护墙、柱壳、穹顶部位应变量测时,选取BX120-50AA 混凝土应变片,电阻为120 Ω,测点分布及编号如图6 所示。
实验所用数据采集器型号为DH5922N,16 通道,最高采样速率为每通道256 kHz。针对2 种实验工况进行了9 次爆炸实验,具体条件及测点分布如表1 所示,Q 为药量,L 为爆心距,H 为爆心高度。

图 6 应变传感器分布示意图 (单位:mm)Fig.6 Distribution diagrams of strain sensors (unit in mm)
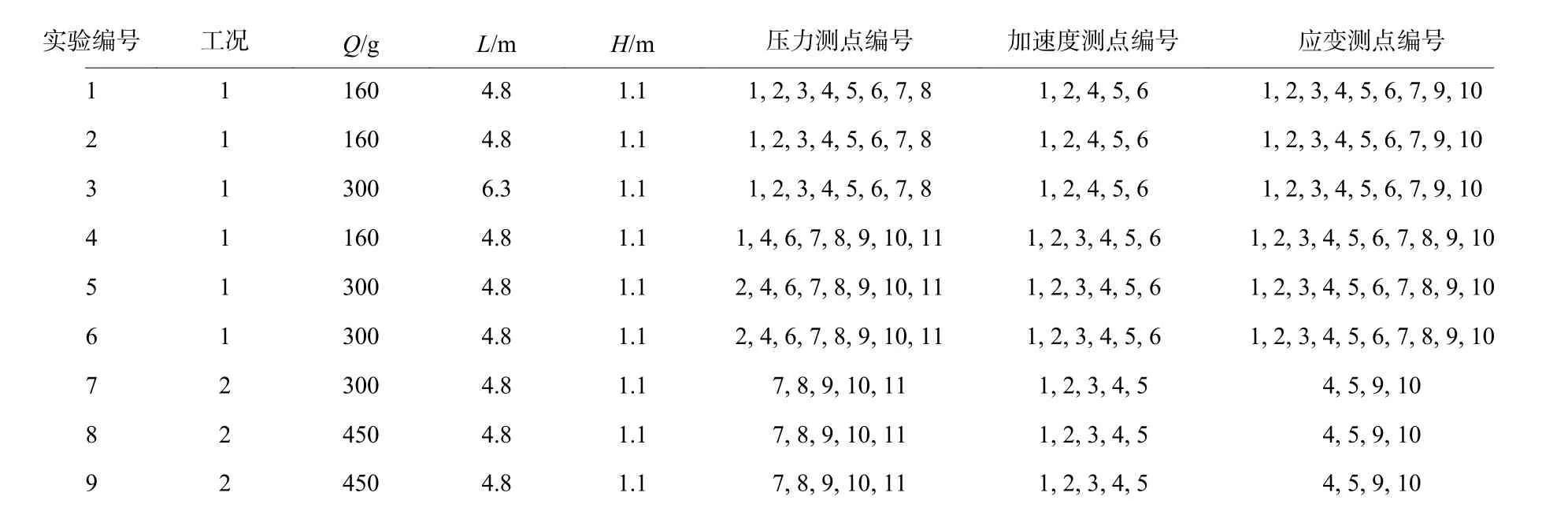
表 1 爆炸实验条件Table 1 Explosion experiment conditions
2 实验结果及分析
2.1 结构外部荷载分布
图7~8 分别给出了2 种实验工况、不同炮次下防护墙和柱壳表面各点的荷载时程曲线。从图7~8 可以看出:相同条件下,各点压力随着药量的增加而升高;对迎爆面来说,冲击波到达后,爆炸荷载先迅速上升至峰值,由于涡流影响再衰减到某一压力值,随后再上升到滞止压力,与防护墙相比,柱壳表面的这一特征更明显;结构表面从迎爆面到背爆面,随着冲击波经过依次产生荷载,峰值压力逐渐减小,峰值到达时间逐渐增加,背爆面荷载峰值上升时间也相对较大,体现冲击波对结构的绕射过程。由于荷载作用时间较短,冲击波到达测点5、11 时,测点1、7 正相荷载基本结束,表明化爆条件下地面空间结构荷载稳态环流相可忽略。
在空气冲击波作用下,柱壳迎爆面部分表面压力由冲击波反射效应产生,后半部分(背爆面)表面压力由冲击波绕射产生,如图9 所示,其中圆形为柱壳横截面。图9(a)中冲击波阵面I-I 以波速 Dφ向右传播,与结构相遇后在A 点发生正反射,该点峰值压力为结构表面最大压力,即图8 中测点7 的压力;除A 点外,冲击波在柱壳结构迎爆面其他各点会发生斜反射,图9(b)为规则斜反射区,R 为反射波阵面;当入射角 φ到达极限角度 φcr时即进入不规则反射区,开始形成马赫波(图9(c));马赫杆(马赫波波阵面)沿结构表面传播并逐渐增高,到达柱壳截面B、C 点时,马赫杆后面出现明显的气体滑流线S(图9(d))[18-19],并在滑流线附近形成涡流,使马赫杆发生弯曲,沿无荷载的后背曲面扩展(图9(e)),呈现绕射效应,涡流的影响随着 Dφ的 增大而增强, Dφ过大时波阵面后面气流速度会超过声速,在结构背面形成膨胀波,涡流和膨胀波在结构背面产生的负压会抵消部分马赫波产生的法向正压,使结构该部分承受的总压力降低,图8(a)显示相同条件下药量较小时,测点10 与测点8 的压力峰值相差不大,随着药量的增大,测点10 的压力低于测点8 的,如图8(c)所示;此后由上下2 个半环面传来的马赫波会在D 点相遇碰撞并产生反射马赫波RMS,使该点压力升高(图9(f));而后RMS 反向传播,气体边界层增厚并形成包含复杂涡流的分离区,冲击波逐渐离开结构表面,随着涡流强度的增大和分离区的扩张,气体滑流线消失,入射冲击波与马赫波M 合并逐渐恢复平面波状。

图 7 H=1.1 m 时防护墙表面各点的压力Fig.7 Overpressure-time curves at various pressure test points on the surface of the protecting wall when H=1.1 m

图 8 L=4.8 m,H=1.1 m 时,柱壳表面各点的压力Fig.8 Overpressure-time curves at various pressure test points on the surface of the cylindrical shell when L=4.8 m and H=1.1 m

图 9 冲击波与柱壳结构相互作用示意图Fig.9 The interaction between the shock wave and the cylindrical shell structure
图10 给出了防护墙和柱壳迎爆面正反射压力时程曲线,正相作用时间约为2.5 ms,测点1 和测点7 在冲击波传播方向相距250 mm,冲击波到达时间相差约1 ms,正反射峰值超压相差约10 kPa,约占最大峰值超压的20%,表明对一般化爆冲击波,在波长与结构尺寸在同一量级的情况下,在确定结构表面冲击波荷载时,应考虑入射冲击波压力在绕射过程中的自然衰减。
图11 表明防护墙迎爆面上,距离地面较近点的荷载较大,主要与空中爆炸条件下传播至结构表面的马赫波高度 HM相关。 HM随传播距离变化并受比例炸高 H/ Q1/3和地面性质影响,若 HM小于结构高度Hstr,可认为结构迎爆面下部为马赫波入射、上部为球面冲击波入射;若 HM≥Hstr,可认为整个结构与马赫波相互作用;若装药距离结构较近,爆炸后可能马赫波尚未形成,仅有球面入射波与结构相互作用。图11中,测点2 主要承受马赫波产生的正反射荷载,测点1 则主要承受球面入射波产生的斜反射荷载,因此测点2 的爆炸荷载要高于测点1 的。此外,Langlet 等[20]的实验也表明,对于地面直立有限长圆柱体,在结构迎爆表面规则反射区域内,不同高度位置承受的荷载有差别,离地面较近的结构表面点的荷载较大,这与本文实验结果是一致的。

图 10 模型结构迎爆面反射压力对比Fig.10 Reflected pressure of the blast side on the model structure

图 11 防护墙迎爆面荷载对比Fig.11 Explosion pressure of the blast side on the protecting wall
2.2 结构振动特性
实验所用装药量较小,产生的爆炸冲击波仅使整体结构发生弹性振动。图12~15 给出了模型结构振动加速度时程曲线,爆源距离L 均为4.8 m,测点1、5、6 体现防护墙的振动特性,测点2、3、4 体现组合壳的振动特性。总体比较而言,测点1 的振动频率较高,测点2、4、5、6 的振动具有低频特征。

图 12 各测点的加速度时程曲线 (Q=160 g,工况1)Fig.12 Acceleration-time curves at various test points (Q=160 g, the first condition)

图 13 各测点的加速度时程曲线 (Q=300 g,工况1)Fig.13 Acceleration-time curves at various test points (Q=300 g, the first condition)

图 14 各测点的加速度时程曲线(Q=300 g,工况2)Fig.14 Acceleration-time curves at various test points (Q=300 g, the second condition)
由图12~15 可以看出:测点1 的加速度体现了爆炸冲击波传播到结构后,防护墙迎爆面部分先产生振动,频率较高,随着防护墙整体参与振动,振动频率降低,振动幅值下降;测点5 主要体现了防护墙整体的振动特性,其振动时间滞后于测点1,最大幅值发生在振动第2 循环,随着防护墙整体参与振动,测点1、5 的振动频率和幅值逐渐一致;防护墙后侧测点5、6 的加速度对比表明,两者的振动频率较为一致,幅值上的差别系由于冲击波绕射到防护墙后侧后对各点的作用不同所致。对组合壳结构,测点4 的振动幅值与测点2 的较一致,但频率在初始时段略低于测点2 的,测点4 体现了组合壳结构的整体振动;测点3 的振动幅值较小,但其振动频率较测点4 的高,且存在2 个明显的峰值。
图16 给出了2 种工况下结构振动加速度时程曲线,对于测点1,工况2 较工况1 的振动频率降低,幅值减小,体现了外部土介质对防护墙迎爆部分构件的防护作用,而对于测点5,工况2 的加速度幅值较工况1 的小,但2 种工况下振动频率较一致,主要由于实验中围土高度及范围较小,围土对防护墙整体振动频率影响不大;对组合壳结构,测点4 表明2 种工况下组合壳整体振动频率一致,但工况2 的幅值较工况1 的小。图17 给出了不同条件下测点3 的加速度时称曲线,图中显示加速度均存在2 个峰值,第1 个峰值随着药量的增大而明显增大;工况2 中第1 个峰值压力要小于工况1 中的,而2 种工况的第2 个峰值基本一致,表明围土对测点3 第1 个峰值有影响,可认为冲击波传播到结构时,环梁先于穹顶受载产生振动,进而引发穹顶振动并形成第1 个加速度峰值,此后随着冲击波绕射时与穹顶相互作用,形成第2 个加速度峰值,该峰值受周围土介质的影响不大。

图 16 2 种工况下各测点的加速度时程曲线(Q=300 g)Fig.16 Acceleration-time curves at various test points under two experimental conditions (Q=300 g)

图 17 不同条件下测点3 的加速度时程曲线Fig.17 Acceleration-time curves at test point 3 under different experimental conditions
图18 ~19 给出了不同工况下模型结构不同部位的应变时程曲线,测点1、2、6、7 反映防护墙的应变,测点9、10 反映组合壳底部的应变。图18 中,测点1 的应变峰值在振动第2 循环,测点2 的应变峰值在振动第1 循环,爆炸波接触防护前墙后,前墙类似于底部固支的悬臂结构,底部应变最大,而后振动频率随着防护墙整体的参与逐渐降低;图18 中还显示测点7 的应变幅值及振动频率均小于测点6 的,测点7 实际上反映了防护墙的整体振动。
从图19 可以看出,测点9 和测点10 的应变最大峰值均在振动第1 个循环,而后逐渐衰减;测点9 的应变峰值大于测点10 的。相同爆炸加载条件下,测点9 的应变值在工况2 时比工况1 时的要小,表明结构周围围土后,在一定程度上增强了圆柱壳的约束作用,使其整体振动幅值减小,这与图16 中测点4 在2 种工况下的加速度对比情况一致。

图 18 防护墙各测点的应变时程曲线 (Q=160 g,L=4.8 m,工况1)Fig.18 Strain-time curves at various test points of the protecting wall (Q=160 g, L=4.8 m, the first condition)
3 结 论
(1)化爆冲击波荷载作用时间短,压力衰减快,结构荷载主要产生于冲击波绕射结构的过程,随着波绕射逐渐施加到结构表面;若结构尺寸与冲击波波长处于同一量级,在确定结构表面荷载时应考虑冲击波压力在绕射传播过程中的自然衰减。
(2)外部爆炸冲击波作用下,结构体现出局部与整体振动耦合的特性,与冲击波最早接触的构件先振动,而后由于结构整体参与使振动频率降低、幅值减小;本实验中结构周边围土降低了防护墙迎爆面的振动频率,减小了防护墙和组合壳整体加速度和应变幅值,但对结构整体振动频率影响不大。
——以徐州高层小区为例

