采用最优场景法求解含风电的无功优化模型

齐晖, 程韧俐，史军，华栋，孙高星

(1.深圳供电局有限公司，广东 深圳 518000；2. 华南理工大学，广东 广州 510640)

无功优化是指在满足一系列物理约束和运行约束的情况下，通过调控发电机无功出力、无功补偿设备输出和变压器变比来优化电网无功和电压的分布情况，从而使有功网损最小或电压质量最高[1-3]。随着具有波动性的风电大规模并入电网，电网出现电压频繁波动[4]，进而出现电压质量问题如电压越限。因此，需研究考虑风电的无功优化模型，以解决风电不确定性给电网带来的电压质量问题，同时降低系统的网损。

含风电无功优化模型的求解在数学上是一个不确定的非线性规划问题，目前主要有两种处理方法，即随机规划[5-11]和鲁棒规划[1-15]。随机规划法又包含机会约束规划法和场景分析法[16]。文献[5]假设风力机模型为异步发电机，风速服从Weibull分布，通过蒙特卡洛方法模拟风电功率，采用粒子群算法求解含风电的无功优化模型。该方法提高了风电不确定性下电网电压质量和系统运行经济性，但蒙特卡洛模拟过程耗时过长。文献[6]利用机会约束规划法求解配电网中多目标无功规划问题，采用基于随机抽样的蒙特卡洛方法提高约束条件的检验效率。结果表明该方法可大幅降低电压越限的风险，但蒙特卡洛模拟限制了算法的效率。文献[7]用机会约束规划法构建了一个两阶段随机优化模型，考虑了负荷和并联无功补偿装置可用性的不确定性。该方法将模型中机会约束转换为确定性的约束，从而将不确定性无功优化问题转化为一个确定性优化问题，最后通过内点法求解。该转换过程考虑约束是线性的，会产生近似误差。机会约束规划需提前给定风速的概率分布信息，并且蒙特卡洛模拟过程使得算法非常耗时，适用于求解周期较长的无功规划模型[8-9]。概率场景分析法是采用不确定性因素的典型场景代替其所有可能发生的场景，利用典型场景发生概率计算目标函数期望值，通过建立期望值模型，寻求满足典型场景下物理约束和安全运行约束的无功电压控制方案。文献[10]建立了含风电机组的配电网无功优化模型，利用场景概率法计算网损的电压偏差值，并采用改进的差分进化算法求解配电网潮流模型。文献[11]对风电机组的出力场景进行探讨，构建了不同场景下的确定性无功优化模型，采用不同的优化算法对各个场景下的模型分别求解，得到不同场景下无功补偿装置的投切方案。同时，在全场景下建立了以网损和静态电压稳定性为目标函数的多目标无功优化模型，并通过改进差分法获取模型的Pareto前沿面。文中表明全场景是能协调各种场景下无功资源的整体最优方案，而某种场景下的最优无功电压方案不一定能满足其他场景下的安全约束。概率场景分析法可在一定程度上解决机会约束规划法耗时长的问题，但未充分利用不确定性因素的概率分布信息，无法准确反映实际模型的情况。鲁棒优化法无需假设不确定性数据的概率分布函数，只需给定不确定集(包括盒式、锥式和椭球不确定集)，寻求能满足不确定集内所有场景约束条件的优化方案。鲁棒优化法理论上只适用于线性(凸)系统，因此在有功经济调度优化中得到了广泛的应用[17-19]。它在求解含风电的有功调度模型时考虑了风电边界场景，从而获得保证电网在风电功率边界处依然能安全运行的鲁棒解。然而，无功优化模型中包含非凸非线性的潮流方程，因此鲁棒优化法无法直接用于求含风电的无功优化模型。一些研究者先将无功优化模型中的潮流方程线性化[12-14]和凸化[15]，再利用鲁棒优化法求解含风电的无功优化模型。文献[12]采用恒功率因数控制模型对风电场进行建模，并将风电功率用盒式不确定集表示，同时对潮流方程进行线性化处理，建立含风电的鲁棒无功优化模型。进一步通过线性优化方法求解，获得模型的最优鲁棒解。测试结果表明，所获得的无功电压控制方案可保证电压在正常范围内波动。文献[15]将鲁棒优化法应用于含风电的配电网无功优化模型的求解。利用锥松弛后的支路电流公式对潮流方程进行凸化处理，将鲁棒优化问题转化成一个混合整数凸规划模型，通过求解转化后的模型得到鲁棒电压控制方案。对比传统的确定性方法，文中的方法计算时间更长，但能获得更优和更安全的可行解。鲁棒优化方法比随机规划法在建模和求解上更简单，但它忽略了风电的概率分布信息，获得的控制方案在经济性上更保守，同时对潮流方程的凸化近似处理会造成模型的近似误差，无法反映真实的潮流分布情况。因此，该方法在求解不确定性无功优化模型的应用受到了限制。

为克服上述方法的缺点和存在的问题，本文提出了一种求解含风电无功优化模型的最优场景法，该方法可以在不使用蒙特卡洛模拟的情况下处理模型中风电的不确定性，同时可充分利用风电的概率分布信息。本文的主要工作包括：

a)建立了含风电的无功优化模型。在无功优化模型的基础上，考虑风电场输出功率的概率分布，同时考虑了风电场3种控制模型，即恒速恒频、恒电压控制和恒功率因数控制，以模拟风电场运行的真实特征。

b)提出了求解含风电无功优化模型的最优场景法。最优场景法包括两个阶段，第一阶段固定离散控制变量(包括无功补偿电容和变压器分接头)，通过调整连续控制变量(包括发电机无功出力)获得各风电场景下的最优控制变量，并计算各场景最优控制变量下的所有场景电压越限次数和越限程度，选出所有场景下电压越限风险最小的控制变量，其对应的场景为称为最优场景。第二阶段固定第一阶段优化得到的连续控制变量，调整离散控制变量使得所有风电场景下电压越限风险更小，同时使平均网损最小。

c)采用标准IEEE 14节点系统和IEEE 57节点系统对最优场景法进行测试，并与机会约束规划方法进行比较，以验证它的有效性和优越性。

1 含风电场的无功优化模型

本节将介绍无功优化模型、风电场模型以及如何在无功优化模型中考虑风电场。

1.1 无功优化模型

1.1.1 目标函数

无功优化的目标是通过控制发电机输出的无功功率、无功补偿装置输出(如电容器组数)和变压器变比来减少网损(或提高电压质量)，网损

(1)

式中：S为系统所有节点的集合；Ui为节点i的电压幅值；θij=θi-θj，θi为节点i的电压相位，所有相位值均以平衡节点的相位为参考；Gij为节点导纳矩阵Y第i行第j列元素Yij的实部。需要注意的是，本文中的参数和变量(相位除外)均采用标幺值。

1.1.2 等式约束

无功优化模型中潮流方程可以表示为

(2)

式中：PGi和QGi分别为节点i发出的有功功率和无功功率；PLi和QLi分别为节点i的有功负荷和无功负荷；QCi为电容无功补偿量，由于其固有的物理特性，取值一般为离散值；Bij为节点导纳矩阵Y第i行第j列元素Yij的虚部。

1.1.3 不等式约束

无功优化模型的不等式约束主要包括发电机无功出力约束、电容无功补偿量约束、节点电压幅值上下限约束和变压器变比约束，分别为：

(3)

式中：SG、SC、ST分别为系统中发电机节点、无功补偿电容、变压器的集合；QGimin、QGimax为QGi的下限和上限；QCimin、QCimax为QCi的下限和上限；Uimin、Uimax为Ui的下限和上限；Tl为变压器l的变比，为离散变量，隐含在Bij和Gij中；Tlmin、Tlmax为Tl的下限和上限。

1.2 风力发电机模型

风力发电机按无功功率的控制模式可分为恒速恒频控制(fixed speed constant frequency type，FSCFT)和变速恒频控制[10]。变速恒频控制又分为恒压控制模式(constant voltage controlling mode，CVCM)和恒功率因数控制模式(constant power factor controlling mode，CPFCM)[20-22]。无论哪种控制类型，风力发电机的输出有功均可表示为风速的函数[23-24]。下面分别介绍风力机的输出功率模型及其3种控制模型。

1.2.1 输出功率模型

风力机的输出功率主要取决于通过其叶片的风速大小[23-24]，可假设它是关于风速的函数。目前风电功率与风速的关系主要有二次函数形式和三次函数形式[23]。但考虑到风力机的实际运行情况，输出功率的风速特性比函数表达形式更为重要。也就是说，在列写输出功率关于风速的表达式时，应进一步考虑切入、切出和额定风速。本文使用的风电机组有功输出功率表达式[12,25-26]为：

(4)

式中：P为风电机组有功输出功率；vci、vco、vr分别为风力机的切入、切出、额定风速；Pr为风力机额定输出功率；A0、A1、A2为计算系数。

A0、A1、A2的取值为：

(5)

风速v为服从Weill分布的随机变量，其分布函数

(6)

式中c和k分别为分布函数的尺度参数和形状参数[23]。

1.2.2 恒速恒频模型

早期的风力机控制技术还尚未成熟，无法实现对风力机叶轮转速的自主控制，因此只能在较小的风速范围和异步模式下发电。在潮流计算时，一般采用PQU节点来模拟风力机的恒速恒频控制模式[20]，即风力机消耗的无功功率

(7)

式中：U为节点电压；R为定子和转子电阻之和；X为定子和转子漏电抗；Xc为并联电容器电抗；Xm为励磁电抗。

随着电力电子控制技术的发展，恒速恒频控制模式风力机的控制技术被更先进的变速恒频型控制模型所取代。

1.2.3 恒功率因数控制模型

恒功率因数控制风力机通过Crowbar电阻和电流互感器用来实现恒功率因数控制，其运行原理可参考文献[12]。它消耗的无功功率

Q=P×tanφ.

(8)

式中φ为功率因数角。

1.2.4 恒压控制模型

恒电压控制的风力机电压由全功率转换器控制，其工作原理与传统发电机相同，并且它具备自主控制风力机无功功率的能力[27-29]，在潮流计算时可当作PU节点处理，只不过其有功输出功率是一个随机变量，其运行原理可参考文献[12]。

3种不同控制类型的风力机可根据其无功功率的控制方式进行区分，其中恒速恒频控制和恒功率因数控制风力机的无功可分别采用式(7)和式(8)计算，而恒电压控制的无功为维持风力机端电压恒定时所需的无功功率。

1.3 风电场接入对无功优化模型的影响

由于受尾流效应、空气对流和叶轮间距的影响[30]，每台风力机的运行状态都不一样。但在实际中，同一个风电场中不同风力机之间的空间位置通常非常接近，呈现出高度的相关性[31]。为简化含风电的无功优化问题的求解，本文忽略同一风电场中不同位置风力机之间的输出功率差异，假设同一风电场中所有风力机属于同一控制类型。基于这一假设，风电场模型可采用风力机模型替代，文献[12]和[14]也采用了类似的处理方式。因此，风电场有功输出功率可当作一个随机变量，其大小取决于风速的大小，风速是服从式(6)中Weibull分布的随机变量，从而含风电场的无功优化模型在数学上是一个带随机变量的非线性优化问题。为方便起见，用向量和函数表示式(1)—(3)中的无功优化模型，并加入随机变量，从而得到含风电场的无功优化模型为：

(9)

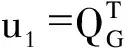
对于恒速恒频控制风电场，需在式(9)的无功优化模型中采式(7)表示其无功消耗，无功功率取决于有功功率和电压，可采用联合迭代法[32]求解潮流；对于恒功率因数控制风电场，采用式(8)表示其无功消耗，在潮流计算时将它当作PQ节点；恒电压控制风电场的无功平衡方程与常规发电机节点的无功平衡方程保持一致。风电场的输出功率是一个随机变量，在输出功率发生波动时，可能导致一些节点电压发生越限，威胁系统运行的安全性，因此需研究出相应的电压控制策略避免电压越限的发生。

2 求解含风电的无功优化模型的最优场景法

最优场景法的目的是降低电压越限的风险和系统网损，由两个阶段组成：第一阶段采用内点法优化连续控制变量选择最优场景，以降低电压越限风险；第二阶段采用遗传算法处理离散控制变量以进一步降低电压越限风险和系统网损。下面将详细介绍最优场景法的原理和算法步骤。

2.1 算法原理

在介绍原理之前，需注意以下3点：

a)存在一个最优场景，在该场景下，最小化系统网损，得到最优的控制变量，可使变量越限的概率最小。也就是说，在最优场景得到一个最优控制变量，对于其他任何场景，电压越限的可能性都是最小的。

b)最大限度地减小网损并不是含风电场无功优化模型的唯一目标。在考虑风电出力不确定性的情况下，降低变量越限的风险，提高系统运行的安全性更为重要。

c)含风电场的无功优化模型既有离散变量又有连续变量，是一个非线性混合整数规划问题，而内点法擅长解决非线性连续优化问题[1]，遗传算法处理含离散变量的优化问题更出色[3]。因此，可将它们组合形成混合优化算法，以结合两类算法的优点。

根据以上3个方面，可以构造一个由内点法和遗传算法组成的混合优化算法来求解含风电场的无功优化模型。该算法分为以下2个阶段：

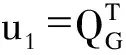
(10)

(11)

2.2 算法步骤

最优场景法求解含风电场的无功优化模型，具体可通过以下7个步骤实现：

步骤1，输入电网和风电数据并设置算法参数。输入电网数据和风电场的数据，设定算法参数包括内点法的收敛精度ε和中心参数δ，遗传算法的种群数量Psize、变异操作的概率Pm和交叉操作概率Pc，最大迭代次数为Ms，置迭代次数k=0。

步骤2，随机生成风电场有功输出功率场景。利用式(4)表示的输出功率表达式和风速的Weibull分布，模拟产生N个风电场景ξ1,ξ2,…,ξN。

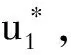
步骤5，判断迭代次数是否满足k>Ms，若满足则停止迭代，进行下一步；若不满足，则继续转到第3步。

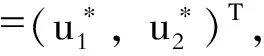
步骤7，输出计算结果。

最优场景法求解含风电场无功优化模型的步骤如图1所示。

3 算例分析

本文将通过两个算例验证所提方法的有效性和优越性。算例1采用IEEE 14节点系统，在系统中考虑恒功率因数控制风电场，将最优场景法与机会约束规划法比较，验证最优场景法的优点和有效性。机会约束方法是目前解决不确定性非线性规划的一种有效而通用的方法，它的目标是搜索约束条件和目标函数满足一定置信水平的解[8]。算例2测试的是IEEE 57节点系统，并考虑恒功率因数和恒电压控制风电场，目的是验证最优场景法两个阶段混合迭代的效果以及算法适应不同类型风电场和大系统的能力。由于恒速恒频控制风电场的技术已经过时，算例中忽略了该类风电场模型。

图1 最优场景法求解含风电场无功优化模型的步骤Fig.1 Procedures of optimal scenario method in solvingreactive power optimization incorporating wind farms

3.1 算例1：含风电场的IEEE 14节点系统

IEEE 14节点系统包含5台发电机、17条传输线、3台变压器和1台电容器，系统接线如图2所示。所有参数的计算均采用标幺值，同时选择100 MVA作为系统的基准功率。发电机有功功率和无功功率上下限的数据见表1。节点电压安全取值范围设置为：负荷节点0.95～1.05，发电机节点0.9～1.1。变压器的变比及调整步长见表2。电容补偿装置位于9号节点，其输出范围为0～0.5，投切步长为0.1。风电场位于10号节点，其控制模式为恒功率因数控制。风电场的切入、切出、额定风速分别为vci=4m/s、vr=16m/s、vco=22 m/s，其额定输出有功功率设为Pr=0.6，功率因数为cosφ=0.95。风速Weibull分布函数的尺度和形状参数分别为c=2.0、k=8.0。

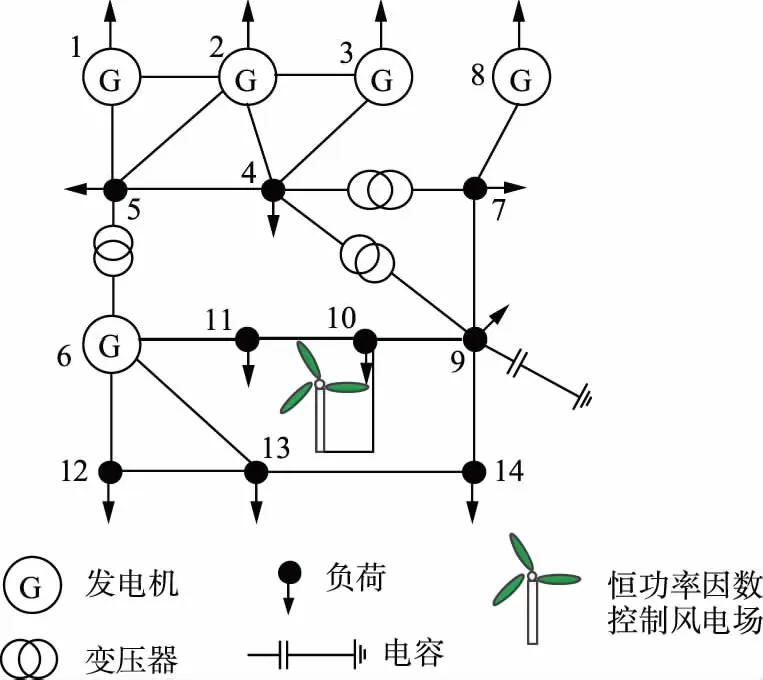
图2 IEEE 14节点系统接线Fig.2 Wiring of IEEE 14-bus system

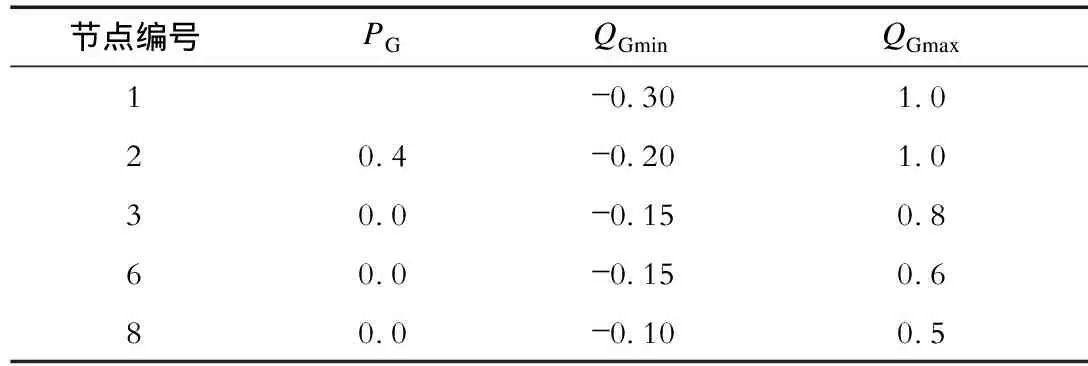
PGQGminQGmax1-0.301.020.4-0.201.030.0-0.150.860.0-0.150.680.0-0.100.5

注：节点1为平衡节点，其有功输出功率未知。

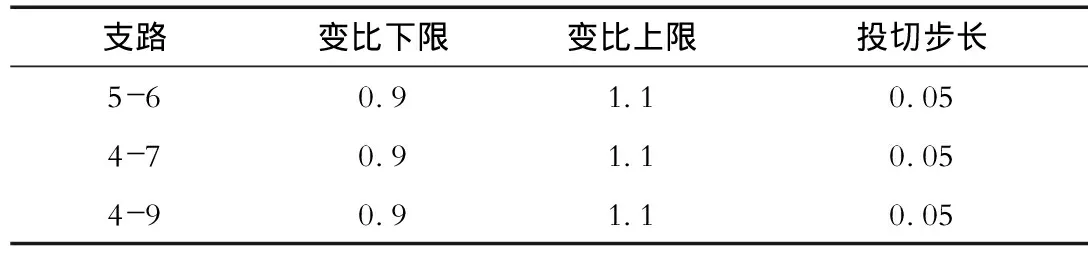
表2 变压器参数Tab.2 Transformer parameters

内点法的参数设置：中心参数δ=0.1，收敛精度ε=10-6。遗传算法的参数设置：种群数量Psize=50，变异概率Pm=0.3，交叉概率Pc=0.2，最大迭代次数Ms=50。首先，对一些具体场景进行分析，并介绍最优场景法的详细算法过程。然后，考虑风速和风电场模型，分析一般情形下最优场景法的测试结果，并与机会约束规划法进行比较。为了便于理解和分析，这里不计算变量的越限量，si中仅含越限次数。同时，算法只执行一次循环，即第一阶段和第二阶段各执行一次。

3.1.1 最优场景法的详细过程

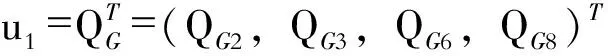
表3 不同场景下变量越限次数和平均网损Tab.3 Out-of-limits times and average power loss of variables under different scenarios

3.1.2 最优场景法与规划约束规划对比

通过对几个具体场景的例子分析之后，进一步将最优场景法用于一般性场景分析，同时场景的产生需要用到式(4)和风速的分布，并将机会约束规划与本文提出的最优场景法进行比较。

首先，通过式(6)给出的Weibull分布得到N=200个的风速样本，再通过式(4)得到一组场景ξ1,ξ2,…,ξN，蒙特卡洛模拟产生的风电场输出功率场景如图3所示。

图3 蒙特卡洛模拟产生的风电场输出功率场景Fig.3 Output power scenarios of wind farm generated by Monte Carlo simulation

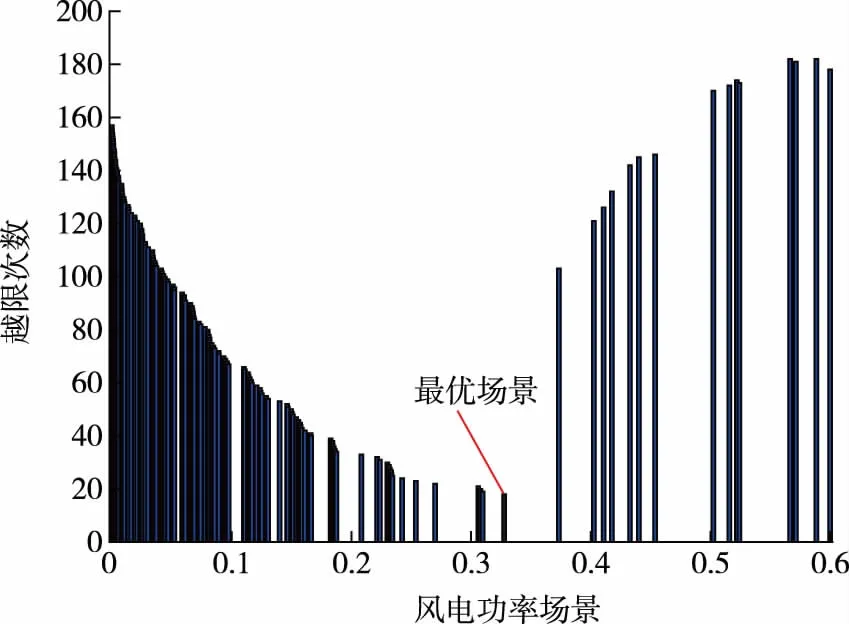
图4 变量越限次数随风电输出功率场景变化的情况Fig.4 Out-of-limits times of variables varying with output wind power scenarios

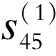
图5 新风电场景下最优场景法状态变量的测试结果Fig.5 Test results of state variables obtained by optimal scenario method under new wind power scenarios

表4 机会约束规划法与最优场景法的比较Tab.4 Comparison of chance-constrained planning method and optimal scenario method

3.2 算例2：含风电场的IEEE 57节点系统

为测试算法中两个阶段混合迭代的效果以及算法的鲁棒性，本节测试IEEE 57节点系统，假设该系统同时包含恒电压控制和恒功率因数控制模型的风电场。该系统包括7台发电机、62条传输线、15台变压器和3台电容器。所有节点电压幅值允许的工作范围设置为0.9～1.1。

在参数设置方面，风电场参数及其相应的风速分布参数见表5。假定恒功率因数控制风电场的功率因数为cosφ=0.95。算法最大迭代次数为Ms=5，取场景数N=200。遗传算法和内点法的参数设置与算例1相同。

表5 风电场参数及其相应的风速分布参数Tab.5 Parameters of wind farms and relevant wind speed distribution

表6 最优场景法迭代结果Tab.6 Iteration results of the optimal scenario method

图6 200个场景对应的变量越限次数Fig.6 Out-of-limits times of variables corresponding to 200 scenarios

为验证最优场景法的有效性，重新生成另外200个风电场景来检验最优控制变量，得到IEEE 57节点系统中所有风电场景下的状态变量如图7所示。从图7可以看出，所有状态变量均处于设定的安全范围内。综上所述，最优场景法可适用于更大的节点系统，同时可获得多风电场并网情形下的电压控制策略。

图7 IEEE 57节点系统中所有风电场景下的状态变量Fig.7 State variables under all wind power scenarios in the IEEE 57-bus system

4 结束语

随着风电接入电网的规模不断扩大，保证风电场并网后电网的运行安全性显得尤为重要。为此，本文提出了最优场景法，目标是降低风电场并网后系统电压越限风险，同时保证网损最小。该算法分为2个阶段：第1阶段通过内点法优化连续控制变量搜索最优场景；第2阶段在第一阶段的基础上通过遗传算法优化离散变量，进一步降低电压越限风险和系统平均网损。通过测试IEEE 14节点系统，表明最优场景法在求解含风电场的无功优化模型时，可得到比机会约束规划法更安全的电压控制策略，同时计算耗时更少。通过测试IEEE 57节点系统，表明最优场景法可适用于更大的节点系统，同时可获得多风电场并网情形下的电压控制策略。虽然最优场景法在求解含风电场的无功优化模型时具有一定的优势，但需从理论上证明它的有效性，同时需探索更高效的算法来代替遗传算法处理离散变量，从而求解大规模电网的无功优化问题。