基于方案（初步）设计阶段的规则桥梁简化抗震设计方法

文｜辽宁省交通规划设计院有限责任公司 周丹

一、成文原因

我国处于世界两大地震带之间，是一个强震多发国家。我国地震的特点是发生频率高、强度大、分布范围广、伤亡大、灾害严重。公路桥梁是生命线系统工程中的重要组成部分。在抗震救灾中起着重要作用。随着这些年地震灾害的不断发生，国内外桥梁抗震技术有了长足发展，我国也借鉴了发达国家的抗震设计技术，并结合国内的具体情况，相继在2008年实施了《公路桥梁抗震细则》，在2011年实施了《城市桥梁抗震设计规范》 。

《公路桥梁抗震细则》较《公路工程抗震设计规范》（JTJ004-89）有了较大改变。不仅扩大了使用范围，设计方法也采用两水平设防、两阶段设计。并增加了延性抗震设计和能力保护原则以及减隔震桥梁的设计原则等内容，为桥梁抗震设计提出了更高标准的要求。

《城市桥梁抗震设计规范》在《公路桥梁抗震细则》基础上引用了基于性能的抗震设计思想（Performance-based Seismic Design），基于性能的抗震设计理论针对不同的结构特点和性能要求,综合考虑和应用设计参数、结构体系、构造措施和减震装置来保障桥梁结构在各级地震水平作用下的抗震性能。

由于我国近些年基础设施建设速度的加快，设计任务量大。按照规范要求，大部分桥梁都需要进行桥梁抗震分析与计算。而规则桥梁约占桥梁总数比例的90%。如何寻求一种方法能快速、准确的判断桥梁的抗震性能，拟定墩柱尺寸，确定支座类型，满足方案阶段及初步设计阶段的要求。

在《城市桥梁抗震设计规范》与《公路桥梁抗震细则》中都已经给出了规则桥梁简化计算方法。但是由于规范中一些参数的取得比较繁杂，而且有些桥梁简化方法还需要建立抗震计算模型，这都大大增加了抗震设计的复杂程度。本文在总结了规则桥梁计算要点的基础上，分析这些参数对整个桥梁抗震的影响，并对其进行相应的简化，总结几种常用类型的规则桥梁的计算规律。通过具体建立有限元模型和简化方法对比分析总结出影响桥梁抗震结果的因素。

二、《城市桥梁抗震设计规范》简化抗震方法参数数据分析

本文以《城市桥梁抗震设计规范》CJJ166-2011 中条文6.5.2～6.5.5 为依据，此规范以下简称为《规范》。规范简化抗震方法只适用于规则桥梁。规则桥梁在跨数、几何形状、质量分布、刚度分布都比较均匀，没有突变，所以规则桥梁地震反应以一阶阵型为主，地震的动力响应相对来说简单。简化方法的计算原理正是将复杂的结构体系转化为单质点体系。

根据地震动微分方程，

m 是质量，k 是刚度，c 是阻尼。质量与加速度相关，阻尼与速度相关，刚度和位移相关，这三者之和与外力平衡，外力为地面的加速度引起的惯性力。

方程有两个参数：自振频率 ω 和阻尼比 ζ。对于大多数桥梁结构，阻尼比为0.05，因此，起作用的独立参数只有自振频率。地震作用的大小与结构的刚度和质量有关，但真正起作用的是它们的比值。

能够准确求出结构的自振频率（自振周期），是求出地震作用的关键。

《规范》6.5.4 中，连续梁周期：

2.1 简支梁桥抗震设计参数简化

S 为根据基本周期计算出的反应谱值。T1为简支梁基本周期。Mt为换算质点质量，其中Msp、Mcp、Mp分别为上部结构质量、盖梁质量、墩身质量。ηcp、ηp是盖梁和墩身的换算质量。求出Mt的关键是求出ηcp和ηp。分别对应振型曲线的墩身计算高度H 处，H/2 处、及基础顶面位移与单位力作用处位移之比。Xhi是用单位力作用下的振型曲线。目的是将墩身各分段质量核算到墩顶，将多质点体系转化为单质点体系。

经过对不同墩高，不同截面单墩模型的位移阵型曲线计算，得到ηp的值在0.22～0.26 之 间。ηcp在0.8～0.9 之 间。 墩身和盖梁在整个换算质量中占比相对较小，ηcp、ηp的取值对整个抗震计算不会产生实质性的影响。

δ 为顺桥向或横桥向作用于支座顶面或上部结构质心上单位水平力在该处引起的水平位移。δ 为对桥梁整体刚度有贡献的所有墩柱的总体柔度。需要注意的是，对于总体刚度有贡献的桥墩数量要根据支座的布置情况来确定。一般认为某一方向固定支座下面的桥墩对整体刚度有贡献，某一方向滑动支座可以自由移动，认为对整体刚度没有贡献。

2.2 连续梁桥抗震设计参数简化

规范中连续梁梁桥地震力的计算分为两种情况。根据支座形式的不同，分为顺桥向只一个支座为固定支座的布置情况（盆式支座或球型钢支座）和板式橡胶支座情况。两种不同支座的布置形式直接影响整个地震力在各个桥墩之间的分配，地震力的分配是按照桥墩的刚度在整体刚度中的比重进行分配的。

1、盆式支座或球形钢支座

《规范》6.5.3 条文，说明的是一联连续梁桥中，顺桥向只一个墩采用固定支座情况下的地震力计算。

固定支座下的墩柱会承担大部分的地震作用，而滑动支座下墩柱因为支座的摩擦系数也会承担一部分地震力。在实际的设计中，桥梁下部墩柱的尺寸一般都保持一致，所以在方案设计和初步设计中，只需要对固定支座下的墩柱进行抗震计算即可。在施工图设计中，非固定支座可适当调整墩柱配筋即可。

2、板式橡胶支座

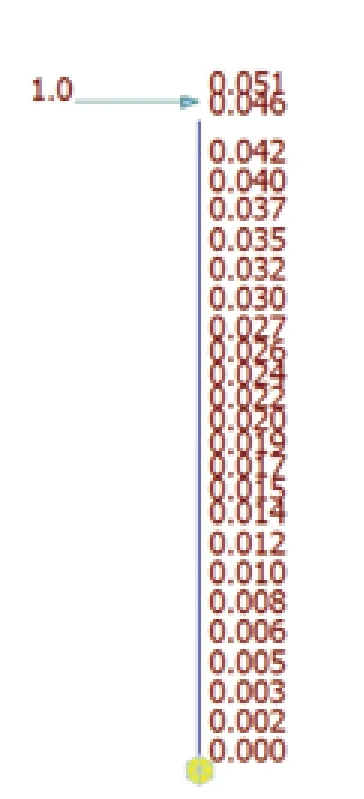
图1.墩柱柔度图

图2.纵桥向一阶频率

图3.横桥向二阶频率

《规范》6.5.4 条文，说明的是采用板式橡胶支座的连续梁桥和连续刚构桥，顺桥向地震力计算。

由以上公式可见，求出一联总的等效刚度是求出基本周期的关键。使用规范方法，需要建立结构计算模型，并且准确模拟支座刚度、地基基础刚度，才能得到等效刚度。本文以下方法无需建立模型，根据力学方法，可以得到满足初步设计要求的基本周期及地震力。

桥梁整体刚度主要是由墩柱的侧移刚度形成的整体刚度。每一个墩柱位置处的集成刚度并联后形成桥梁整体刚度。而每一个墩柱的集成刚度是由墩顶几排支座并联后与墩柱刚度串联后的刚度。

其中，Kl为桥梁等效刚度，Kij为墩柱与支座的集成刚度，K墩i为各桥墩的抗推刚度，K支i为支座的抗推刚度，G 为橡胶的剪切模量，ΣA支为支座承压面积总和，Σt 橡胶支座中橡胶片的厚度总和。

根据等效刚度求出基本周期，根据，Ektp=SMt求出总的水平地震力。每一个墩柱所承受的水平地震力按照每一个桥墩的集成刚度K墩i在总的等效刚度Kl中的比重，进行地震力分配，然后按照规范进行抗震计算即可。

表1 简支梁单墩模型计算基本周期参数值

三、依托实际工程对比简化方法与模型方法结果

3.1 简支箱梁抗震对比

现以一跨32 米混凝土简支箱梁为例，运用简化方法与MIDAS 建立空间模型的结果进行对比。此工程上部结构为单跨32m混凝土箱形截面，横桥向为双墩（无盖梁），墩柱直径1.8 米，墩高9.7 米。支座约束情况：纵桥向一个桥墩为纵向固定约束，一个桥墩为纵向移动约束。横桥向两个支座，一个为横向固定支座，一个为横向移动支座。

基本周期计算:

建立单墩模型，墩底约束考虑桩土共同作用效应，在桥墩支座顶面高度处施加单位力。取得单位力作用下的振型曲线。单个墩柱模型中查得该处的水平位移，为单个墩柱的柔度。横桥向两个墩柱的共同柔度为一个墩柱柔度的一半。从单墩模型中查得δ1=0.051×10-3m，所以δ=0.026×10-3m。

查看MIDAS 空间梁单元模型结果，第一振型为纵桥向振型，基本周期为1.14，基本吻合。

多媒体信息技术在初中语文课堂教学中的作用是不可磨灭的。它让学生更直接地了解到课文中的一些问题，让学生对课文的理解更透彻、更直观。多媒体技术在语文中的运用，不仅对激发学生学习兴趣，突破教学重点和难点，加强师生间的信息交流和反馈，提高语文课堂教学的效率能起到事半功倍的作用，还有利于形成学生的自主、合作、探究的学习方式，促进学生创新思维、综合性学习能力的提高。但是，任何教学方法、手段的选择，都是为达到所设的教学目标、取得最佳的教学效果服务的。而且，作为现代化的教学技术手段，也并非每一课都适用。

因为横桥向无盖梁，横桥向周期计算方法同纵桥向计算。

查看MIDAS 空间梁单元模型结果，第二阵型横桥向周期，T2=1.12s 与简化方法计算结果T=1.156s 小了3.6%.分析原因由于空间模型中桥墩和主梁形成框架，这种框架效应横桥向影响稍大些。

3.2 连续梁桥抗震对比分析

算例2 为三跨连续梁桥3×32=96m，上部结构为箱梁，横桥向设置两个圆形墩柱，直径为1.8m。支座为普通盆式支座，边中墩跨径线处设置纵桥向约束，其余跨径线处顺桥向放开。横桥向两个支座，一个固定约束，一个移动约束。

1、顺桥向计算

连续梁顺桥向水平地震力由纵桥向约束的两个边中跨处支座进行承担。

查看MIDAS 空间梁单元模型结果第一振型为纵桥向运动，基本周期为1.998s，结果吻合。

2、横桥向计算

在规范6.5.5 连续梁横桥向计算需要建立有限元模型进行计算。本文按照刚度分配理论，对横桥向无横向联系的桥梁只需建立单墩模型，来求得横桥向的周期。

本文方法建立单墩模型方法计算：

根据连续梁桥的横向约束情况。整联桥梁横桥向一共由4 根墩柱承担横桥向水平荷载。那么整个桥梁的整体横桥向刚度就是一个墩柱柔度的1/4，总体δ=0.052×10-3/4=0.013×10-3。

按照规范建立有限元模型计算：

根据《规范》6.5.5：连续梁桥横桥向等效刚度Kt：

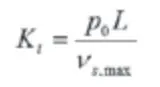
P0为沿计算模型（包含边界联）横桥向作用于主梁的单位力。vs,max为单位力作用下结构横桥向的最大位移。L 为计算模型总长。

按照规范要求建立结构计算模型的方法，求连续梁桥的横桥向基本周期。在MIDAS 空间梁单位模型上，横桥向施加均布力10KN，查得结果横桥向结构最大位移为0.014m。

在MIDAS 空间梁单位模型上查得横桥向振型的基本周期为：1.50s，吻合。

从以上计算结果比较可以看出，对于连续桥梁横桥向计算，框架效应的影响更明显，横桥向的周期按照本文思路算法比规范算法稍小一些，这个周期范围在反应谱曲线的下降阶段，周期越小，算出的地震作用越大，所以，在连续梁桥横向计算方法上，运用本文思路求得的基本周期是偏于安全的。

四、简化方法计算要点归纳

1、规则桥梁的地震力与结构的刚度和质量的比值有关，也就是结构的频率或基本周期。

2、盖梁和桥墩的质量换算系数是用能量法或者代替质量法将墩身各分段质量核算到墩顶，简化为质点质量处理，避免了多质点体系基本周期的复杂。质量换算系数能大体确定在一个范围内，其值对结果的影响不大。

3、桥梁的整体刚度是由桥墩和支座的合成刚度决定的，哪些桥墩和支座会对整体刚度有贡献，取决于支座的类型和分布情况。板式橡胶支座，每个支座的刚度相差不大，能将地震力均匀分布于每个桥墩，有利于结构对地震能量的扩散。盆式橡胶支座或者球型钢支座将大部分地震力集中于固定支座处的桥墩，使固定墩承受较大的水平地震力。

4、对于桥梁横桥向的地震作用，由于横桥向刚度受结构形式变化影响很大，横桥向有横向联接（盖梁、系梁）等情况，本文未做阐述。但总体思路依然是求出横桥向的刚度是求出地震力的关键。

表2 连续梁单墩模型基本周期参数值-纵桥向

表3 连续梁单墩模型基本周期参数值-横桥向

表4 连续梁规范方法基本周期参数值-横桥向