基于PCCs-DEMATEL指标筛选的BP神经网络用水量预测

崔惠敏，薛惠锋，王 磊，赵臣啸

(1.西安理工大学，西安 710000; 2.中国航天系统科学与工程研究院，北京 100048)

国家“十三五”规划纲要明确提出“实行最严格的水资源管理制度，以水定产、以水定城，建设节水型社会”等要求。水资源分布不均衡、配置机制不完善等问题制约着我国节水型社会的建设进程，面向决策支持的用水量预测研究是水资源优化配置的数据支撑，是水资源应用研究的重要组成部分[1]。现有文献中存在许多用水量相关预测方法，适用于地区水资源合理配置。其中，短时间内日用水量预测多用于供水系统的优化调度和设备检测管理，年度中长期用水量预测多用于对城市建设、生态保护提出决策建议。

国外研究者对于水资源趋势预测分析更多的是对算法进行优化。G-CHEN等[2]提出了一种多随机森林模型，集成小波变换和随机森林回归(W-RFR)用于城市用水量的预测。使用离散小波变换(DWT)分解，并用随机森林回归(RFR)方法对每个子系列进行预测。LCP Velasco等[3]利用人工神经网络(ANN)分析城市用水决策数据，使用Neuroph Studio进行数据准备、模型模拟和预测结果的测试。TMF Jr等[4]利用滞后的天气状况历史数据和以前记录的用水量来预测8个区域的需求量。国内研究者在预测方面研究了相关因素对用水量的影响。李斌等[5]预测短期市区供水系统用水量，使用组合预测权重系数优化指标，并对灰色-神经网络的二元组合进行求解。郭磊等[6]分析了总用水量与地区生产总值的负相关性，构建了基于相关性分析结果，构建了基于经济、人口为自变量的趋势模型。景亚萍等[7]分析比较不同预测模型使用效果，构建组合灰色神经网络预测模型，并运用马尔科夫链进行修正，获得高精确度的预测值。王开章等[8]运用灰色理论模型，通过精度检验，不断进行模型修正，对水源地的水质变化趋势进行了预测分析。

综上，现有水资源预测模型的算法包含许多智能算法，其中在选择预测所用的影响因子时，论证不够充分、合理，主要依赖于一些定性分析。统计指标涵盖了多项影响因素，历史数据反映出各因素对用水量指标产生的复杂影响。构建完备、适合的指标模型，有利于分析影响用水量的关键因素，从而可以更全面、准确地预测用水量，为水资源管理决策提供完备、高效、准确的定量数据支撑。本文采用定性与定量相结合的方法[9]，针对统计数据，应用DEMATEL(Decision Making Trial and Evaluation Laboratory，决策试验评估实验室)方法作定性分析，应用皮尔逊相关系数作定量分析，对与用水量相关的指标进行分析筛选，利用BP神经网络3层结构模型对年度用水量进行预测，为国家资源宏观调控提供数据支撑。

1 理论方法

1.1 皮尔逊相关系数

皮尔逊相关系数PPCs(Pearson correlation coefficient)是由统计学家卡尔·皮尔逊在前人的基础上改进得出的。皮尔逊相关系数用于定量地衡量变量间相关程度，标准值介于-1到1之间。针对2个变量之间的皮尔逊相关系数，函数定义为变量协方差与标准差的商值，计算公式如下：

(1)

式中：R为相关系数；X与Y分别表示2个用于比较的变量。

皮尔逊相关系数已经应用于异常检测、医学信号相关度测量、光热试验影响分析等多种研究领域[10-12]。

1.2 DEMATEL

1971年Bottele为研究解决现实世界里复杂问题，提出了DEMATEL方法论。该理论运用图论以及矩阵工具进行系统要素分析，判断要素间强弱的因果关系[13]，充分利用专家的知识与经验来处理复杂的问题，通过筛选主要的影响因素，从而实现对系统结构的简化分析。方法实现需要进行以下步骤：

(1)确定不同因素间的关联关系，构建直接影响矩阵，并进行规范化处理。

(2)

(2)规范化直接影响矩阵G，计算系统影响因素指标间的综合影响矩阵T。

(3)

T=G+G2+…+Gn

(4)

T=G(I-G)-1

(5)

一般情况下选择公式(2)计算综合影响矩阵，但当我们所需分析的指标数量足够多时，我们也可以采用公式(3)进行近似计算。

(3)计算指标的影响度fi与被影响度ei。

(6)

(7)

(4)计算指标的中心度与原因度。中心度的计算方法是将影响度与被影响度相加。对于研究对象而言，获得的中心度数值越大，影响力表现越大，反之则越小。原因度是将影响度与被影响度相减，当2者数值大于零时，则该因素为原因因子，反之则为结果因子。

mi=fi+ei

(8)

ni=fi-ei

(9)

1.3 BP神经网络

BP神经网络是一种采用误差反向传播原理的前馈神经网络，学习方式是将输入与输出的映射转变成一个非线性优化的问题，使用梯度下降算法，多层迭代修正网络结构间的权重，从而使得预测值与实际值间相对误差逐渐减少。网络结构由3层构成，分别是输入层、隐含层、输出层。其网络拓扑结构见图1。

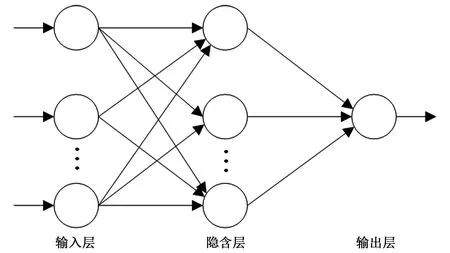
图1 BP神经网络拓扑图

2 指标筛选与预测方法

2.1 现有指标汇总

现有文献在影响用水量指标分析上，普遍选取了人口、工业水平、人民生活水平以及社会经济水平、气候变化等因素。《变化环境下城市用水量影响因子识别》一文[14]认为东莞市用水量影响因子涵盖年末总人口、GDP、农业总产值、工业总产值、第三产业增加值、年平均气温、年降雨量、降雨量大于0.1 mm的天数和日照时数等。《免疫进化算法和投影寻踪耦合的水资源需求预测》[15]一文认为用水量与GDP、工业总产值、农业总产值、有效耕地面积、实灌耕地面积、农业用水系数、城镇人口、农村人口、城镇供水利用系数、牲畜数量、水重复利用率、居民人均可支配收入等指标关联性较高。王丽霞、任志远、孔金玲等人[16]选取工业生产总值、农业生产总值、人均GDP、城镇人口数、农村人口数、万元工业产值用水量、万元农业产值用水量、人均日生活用水量、农田有效灌溉面积、牲畜量、居民生活、农业生产和工业生产总用水量等10个因子作为延河流域用水量预测的关键驱动因素。

本文在已有研究的基础上，通过文献整理与网络调查归纳出广东省地级市水资源统计数据在人口、经济、地理、水资源4个层面共28种影响因素，并用A1、A2、…、G27、G28分类表示，结果见表1。依据研究地区的特定属性以及普遍认可的用水量预测的普适因子进行汇总。

表1 统计指标汇总

2.2 指标筛选

水资源受人口、经济、地理等多种因素影响。其中，既存在与用水量高度相关的指标，也存在关联度较弱的指标。本文采用从定性到定量的综合集成方法对指标进行筛选，构建科学合理的与用水量关联的指标体系。

2.2.1 数据来源

统计28个指标因素在广州的原始数据，为确保所有指标均有数据，时间范围划定为2005-2016年。数据来源为广州市统计局统计年鉴、广州市水务局水资源公报。

2.2.2 定性分析筛选

用DEMATEL方法对指标进行定性分析，定量描述。

首先以5级量表法对不同指标间相关性进行打分，得出初始的直接影响矩阵。指标因素i对j的影响层级分为5级，强相关、较强相关、一般相关、较弱相关、无关，每层对应的分数分别是7、5、3、1、0，对属于层级之间的关系，以2、4、6给予评分。在此次调查中，专家组由7名长期从事水资源研究工作的人员组成。其中包括2名国家水利部工作人员、3名省级水利厅工作人员、2名高校水资源专业教授。将打分表取平均值，对小数部分进行四舍五入，保留到整数位。根据公式(3)进行矩阵的规范化处理，根据公式(5)计算综合影响矩阵。

根据得到的综合影响矩阵，依照公式(6)、(7)分别计算指标间的影响度与被影响度，进而得出指标间关系的中心因子与原因因子。在笛卡尔坐标系中，依据因素指标的中心度与原因度标记出每个因素所处的位置，分析不同水资源指标在用水量预测中的重要性。由于主要考虑的是指标的影响程度，因此以中心度的值作为计算数据进行后续计算。

2.2.3 定量分析筛选

从指标的真实数据入手开展指标关联分析，分析冗余性。运用皮尔逊相关系数计算汇总指标与用水量关联程度并排序，从而筛选出高关联度的指标作为预测的参考因素。

首先对数据进行无量纲化处理，每一个指标除以该列最大值。其次选择用水量作为参考数据，其余28项指标依次作为对比数据，依照公式(1)计算皮尔逊相关系数。

考虑专家意见具有较强的随机性，将定性分析得到的中心度和定量分析得到的相关系数分别以40%、60%比例加和，将计算结果按照从高到低的顺序依次排列，结果见表2。计算取值范围的中位数，结果为0.815 5。选择影响程度综合排名高于0.815 5的指标因素作为预测时的考量信息。

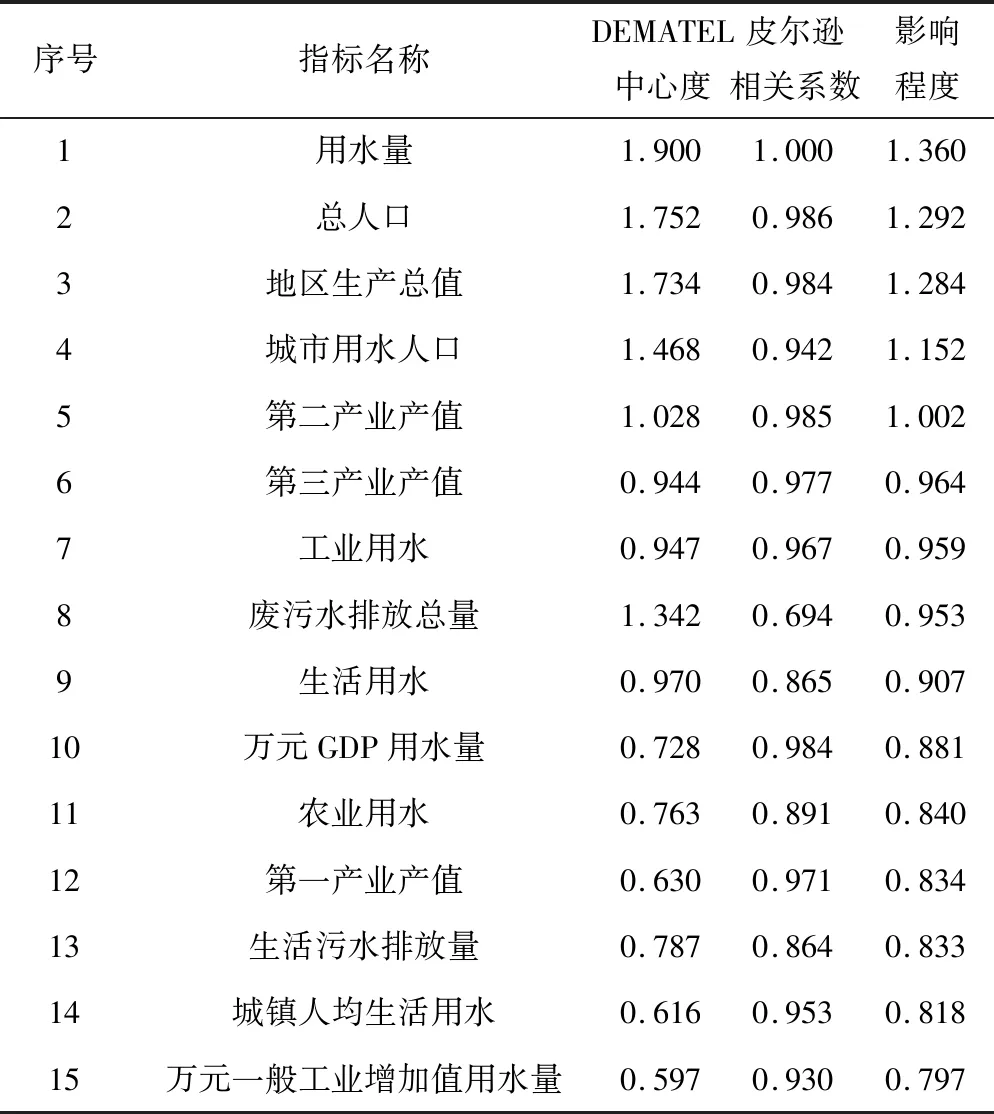
表2 指标筛选结果

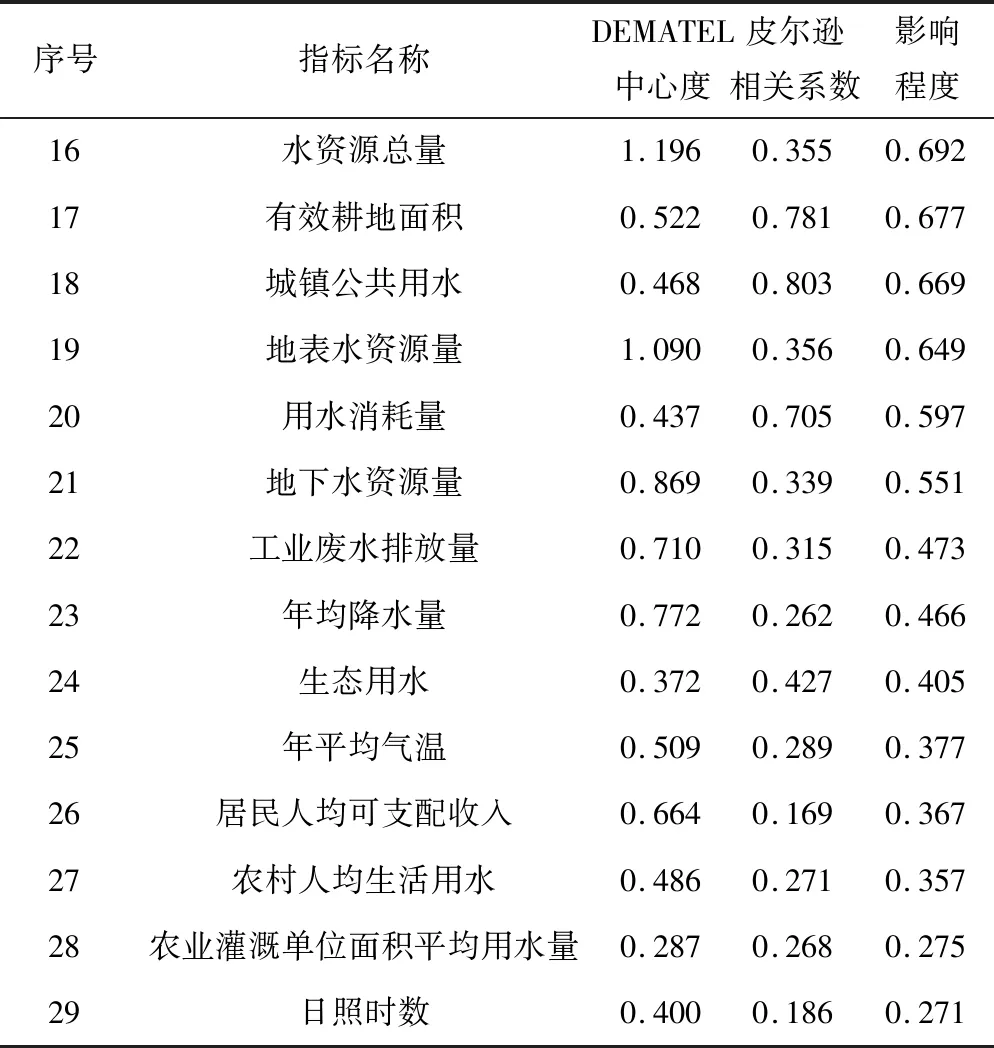
续表2 指标筛选结果

2.3 用水量变换趋势预测模型

2.3.1 BP神经网络预测模型

(1)统计数据处理。为了体现趋势动态变化过程，分析用水量变动特征，从而更好地进行预测，不直接采用历年的直接统计数据作为考量信息，而是首先计算统计数据的同比变化率pi，作为预测模型的输入量。

pi=(xi-xi-1)/xi

(10)

式中：xi为第i年用水量。

(2)归一化处理。统计数据属于不同的量级，应首先对原始的统计数据进行归一化处理，选择mapminmax归一化函数分别对训练集的输入输出矩阵、测试集的输入输出矩阵进行处理,将其数值归一化到[-1,1]。

(3)网络结构设定。神经网络的结构将直接影响网络预测结果的准确性。网络输入层包含的14个节点分别对应于本文所提出的指标体系中的14个指标。输出层共包含1个节点，输出用水量预测值。

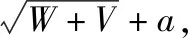
(4)结果评价。将预测出的同比变化率转化为实际的用水量数据，使用相对误差和决定系数进行结果评价，相对误差越小，精确度越高，决定系数越接近1，拟合效果越好。计算公式如下：

(11)

(12)

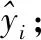
2.3.2 参照对比赋权指数平滑法

水资源统计数据具有时序性，在对时间序列数据进行预测时要充分考虑其时间价值。一般认为距离预测时间较近的数据拥有更高的时间价值。因此在预测分析时对各个时期的数据赋予不同的使用权重[18]。

假设当前时间为t，各观测时间的用水量记为X1,X2,…,Xt，进行连续n个时期的时序记录，下一时期将预测t+1阶段的数值Xt+1，不同时段数据的时间价值权重依次表示为：

(13)

进行归一化处理的结果：

(14)

预测计算公式：

(15)

(n≥2)

3 实例研究

3.1 模型应用

(1)BP神经网络预测模型。2005-2016年的统计数据包含12条信息，首先计算2006-2016年指标变化率pi，得出11条信息作为基本指标。将前一年的14项基本指标变化率作为输入，当年的用水量变化率作为输出，一共构成11条样本。选择其中9条样本作为训练集，以整体样本作为测试集。经过多次调试，当隐含层的节点数为10时，模型预测效果最好。调用MATLAB工具箱，选择节点数为14-10-1模型，设置相关参数，迭代次数设置为50次，训练目标为1e-8，学习率为0.01。将模型计算出的年度预测变化率转化为用水量，并计算与实际用水量之间的相对误差和决定系数。

(2)赋权指数平滑法。利用模型公式，代入用水量历史数据进行计算，得到结果见表3。

比较BP神经网络预测方法与赋权指数平滑法在用水量预测上的准确度，作为预测结果的分析依据。

3.2 预测结果分析

图2为BP神经网络模型预测结果与实际值的比较，图3为BP神经网络对训练样本的拟合效果，可以看出BP神经网络能很好地拟合用水量趋势变化量。

已有文献中通常基于指标原始数据对用水量进行预测，这种方法往往无法体现用水量动态变化趋势，利用变化率预测能够更好地体现这一状态，且用水量变化率包含多级小数位，对于误差的逆向传播提供了更高的精确度。本文以用水量年变化率pi与上年度用水量的乘积表征用水量预测值，能够更好地满足用水量预测的精度要求。

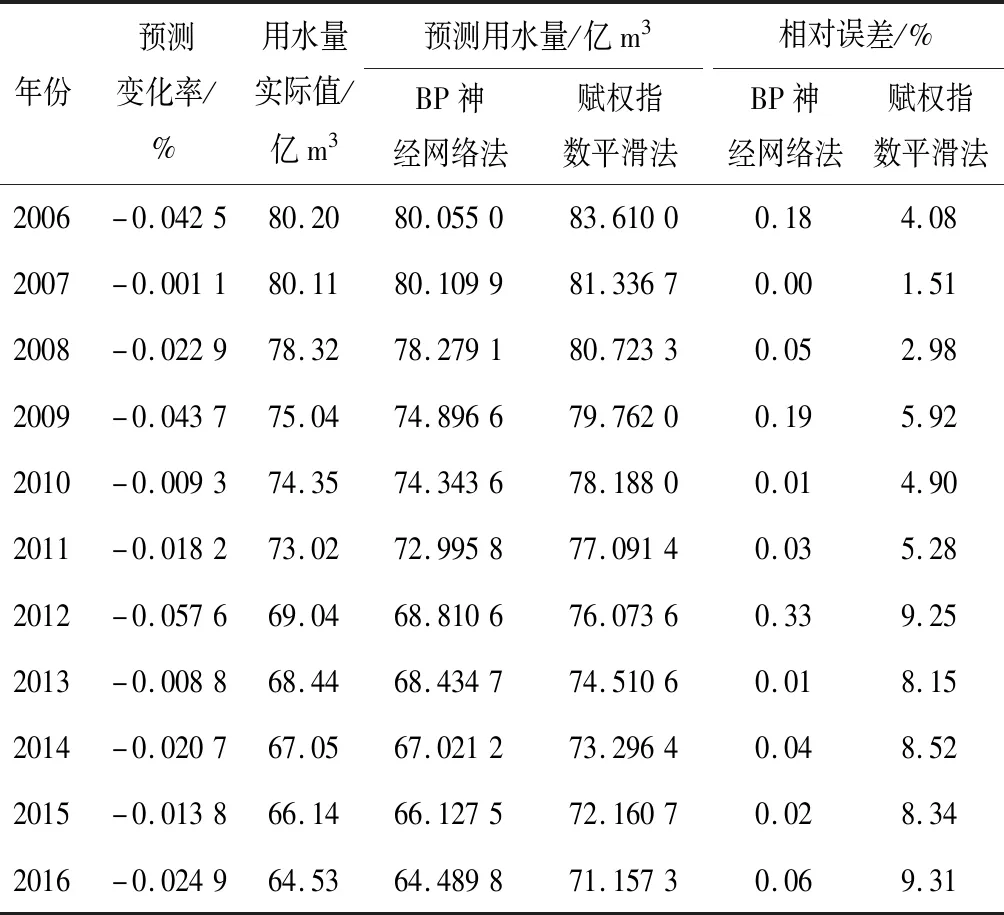
表3 预测结果分析

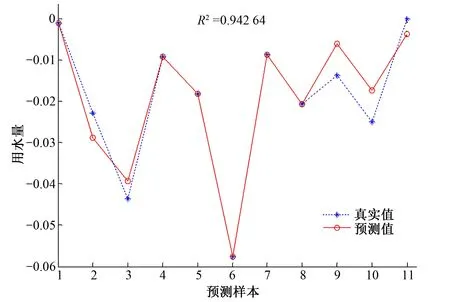
图2 测试结果与实际值对比

图3 BP神经网络对训练样本的拟合效果

表3是测试用水量预测结果对比。原始数据从2005年开始，计算后的同比变化率从2006年开始，分析前述评价指标，其中决定系数为0.942 6，相对误差见表3，相对误差为0.000 1～0.003 3，取得较高的准确度，说明神经网络的结构模型适合用于多统计指标的以年为基本单元的中长期用水量预测。

依据相对误差的比较，BP神经网络与赋权指数法2者的相对误差在精确度上超过2个数量级，BP神经网络模型的优势格外显著。赋权指数平滑法在试验过程中，虽然给予时间序列数据以递增的权重，但对于以年为单位的较大用水量数值，即使是个位数的变动对整体也有很大影响，单纯数理上的加和缺乏科学性、合理性。

BP神经网络的合理应用离不开输入层指标的设置，将影响用水量的指标通过定性与定量相结合的方法进行筛选。从筛选结果上看，影响用水量的主要指标集中在人口因素、经济因素上，地理因素虽然会对水资源产生影响，但因为其自身状态的稳定性，趋势变化不明显，对于用水量的预测参考价值低。另外，用水量数据出现连年下降的趋势，降幅比例没有明显变动规律，但下降趋势非常稳定。本文分析研究了广州市用水量统计数据，发现工业用水在用水总量中占据较大比重，而用水总量持续下降，反映出广州市的水资源利用效率伴随经济社会发展持续提高。

4 结 语

为保障资源的合理利用，采用准确、高效的预测方法对用水量进行预测至关重要。对于大量的历史统计数据，本文提出一种更全面、准确的基于PCCs-DEMATEL指标筛选的BP神经网络用水量预测模型。使用广东省广州市统计数据作为基础数据进行实证研究，与传统的、单一的基于时间序列的赋权指数平滑法进行比较分析，证实了本文提出的模型方法更具优越性。本文提出的这种研究模型也可以应用到水资源其他关键指标的预测分析上，比如废水指标中的入河废污水量、废污水排放量等，从而可以根据预测结果进行除污设备有效设置、突发事故预防等先决性工作指示。水资源相关指标的预测工作为国家实施最严格水资源管理制度提供了定性与定量相结合的、可靠的数据支撑。