基于组合赋权的改进尼梅罗指数法在地下水水质评价中的应用

骆茂林，罗 欢，李中阳，张金林，张 强

(成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都 610059)

随着我国工农业的发展和人口的不断增长，对淡水资源的需求量不断增加，而地下水资源作为相对清洁、稳定的水源，已成为维系我国缺水地区经济社会发展不可或缺的因素[1]。而切实、合理的地下水质量评价是使地下水在各级水质标准范围内充分发挥其作用[2]，防止出现因水质评价过轻而导致的水中毒或因评价过重而导致的水资源浪费等问题的前提保障。目前对于地下水质量评价的方法主要有：单指标法[3]、模糊综合评价[4,5]、尼梅罗指数法[6]、物元可拓法[7]、投影寻踪法[8]、人工神经网络[9]、贝叶斯模型[10,11]、灰色关联度法[12]、集对分析法[13]、主成分分析[14]等方法。不同的评价方法对同一水质监测数据会得出不同的评价结果，都存在着各自的优点和不足，有学者还对此作了大量对比研究[15,16]。尼梅罗指数法凭借计算过程简便、物理概念清晰、评价结果较符合实际等特点被广泛应用。但传统的尼梅罗指数法存在单项组分评分不连续和过分夸大最大污染指标的缺点。针对此问题，本文结合熵权和二项系数主客观融合权重对尼梅罗指数法予以改进，以寻求评价结果更具客观准确性。

1 评价方法与原理

1.1 熵权法

熵权法是一种成熟且应用广泛的客观赋权方法，它根据各评价指标的变异程度来确定不同评价指标的权重。变异系数越大，表明该指标的信息量越大，越应该给予较大的权重。

现在假设有m个待评价对象，记为M=(M1，M2，M3，…，Mm)，n个评价指标，记为D=(D1，D2，D3，…，Dn)，则待评价对象对应的评价指标的值构成的原始数据矩阵为X=(xij)m×n。其中xij为第i个评价对象在第j个指标上的值。

(1)对评价指标进行标准化处理。由于评价指标的单位不尽相同，且数据变化幅度较大，需要对矩阵X进行标准化处理，得到矩阵V=(vij)m×n。标准化处理后所有的值都介于0～1。标准化处理分为越大越优型和越小越优型。

对评价指标越大越优型，选择标准化公式：

(i=1，2，3，…，m；j=1，2，3，…，n)

对评价指标越小越优型，选择标准化公式：

(i=1，2，3，…，m；j=1，2，3，…，n)

(2)计算第i个对象在第j项指标下的特征比重pij。计算公式为：

(3)计算第j项指标的熵值Hj。即：

(4)计算第j项指标的变异系数Kj。当Kj越大时，该指标的信息量越大，越应给予较大的权重。计算公式为：

Kj=1-Hj

(5)确定各个指标的熵权。即：

1.2 二项系数法

常用的主观赋权方法有层次分析法、专家打分法、二项系数法。本文选用较为简便的二项系数法，该方法先由决策者比较相对重要性，然后对所有评价指标的重要性进行总排序，再对评价指标进行对称排序，最后根据二项系数加权和的计算公式得出各指标权重。

(1)假设有n个评价指标，分别标记为X1，X2，X3，…，Xn。经过决策者的评判比较得出相对重要性顺序，记为：

(2)依据重要性最强的指标放中间，次重要的指标对称放两侧的原则，重新排列为如下形式：

(3)利用二项系数加权和法计算各指标权重：

式中：i为第j项指标按对称排序后的位序。

1.3 组合赋权法

组合赋权即将不同赋权方法得到的权重予以结合，克服单一赋权方法的不足，提高所取权重的可靠性和可信度[17]。本文采用乘法归一化组合赋权法[18]，将熵权法所得的客观权重αj与二项系数法所得的主观权重βj进行组合，组合公式如下：

1.4 传统的尼梅罗指数法

尼梅罗指数法是由美国叙古拉大学的尼梅罗(N.L.Nemerow)教授提出的，旨在解决单指标法评价水污染不全面的问题的评价方法[19]，其计算步骤如下：

(1)根据地下水质量标准(GB/T 14848-2017)，划分不同评价指标下实测值的质量类别。

(2)参照表1根据质量类别赋予某一样本在某一指标下的分值Fi。

表1 地下水质量评分结果

(3)计算Fi的均值。即：

(4)计算某样本的综合得分值，并根据表2得出水质综合等级。即：

表2 地下水质量分级

1.5 改进的尼梅罗指数法

限于尼梅罗的计算公式，实际上放大了最大污染指标的作用，未能充分考虑各指标对水质的贡献程度，不能全面地评判样本的水质，而且尼梅罗指数法的水质质量评分表(见表1)中的数字是0，1，3，6，10共5个间断的数字，难以表征连续的实测结果。针对以上问题，前人已经对尼梅罗指数法作过一些修正[20-26]。蔡晔[20]，谷朝君[21]，杨磊磊[22]等用最大权重指标对应的得分值与最大得分值的平均值代替原来的最大值，但是没有考虑Fi的连续性问题；李玲玲等[24]将Fi的算术平均值与最大值取算术平均，来代替最大值，这过分削弱了最大值，导致评价结果失实，且没有考虑Fi的连续性问题；寇文杰[25]考虑到了Fi的连续性问题，提出了一种修正方法，但因为修正后的Fi小于修正前，所以最后的结果也比修正前小，影响了结果的准确性；倪天翔[26]提出了对Fi的修正公式，并用m(规定m一般取5)替换n(评价指标的个数)来给平均值加权，但是并没有真正意义考虑每个指标的权重，只是根据经验取的m值。本文采用已有的连续公式[26]，同时对Fi求加权平均，用权重最大指标的得分值Fwei和最大值Fmax的平均数来代替最大值Fmax，具体计算步骤如下。

(1)求Fi的加权平均值。即：

(2)计算综合得分值。即：

2 实例应用

研究区位于湔江冲洪积扇的中上端，地势西北高、东南低，地下水流向与地势走向基本一致；地下水类型主要为松散岩类孔隙水，大气降水为主要补给源。本文选用研究区2018年5月水质检测资料作为原始数据，根据水质检测结果和指标重要程度选出氨氮、总大肠菌群、铁、锰、总硬度、溶解性总固体、pH、氯化物、硫酸盐、硝酸盐、氟化物等11个指标共9组数据为研究对象(见表3)。

2.1 确定各指标权重

依次运用熵权法和二项系数法求取各评价指标对水质污染的贡献值，即权重，再运用组合赋权公式将2种方法的结果融合得到组合权重。权重结果见表4。

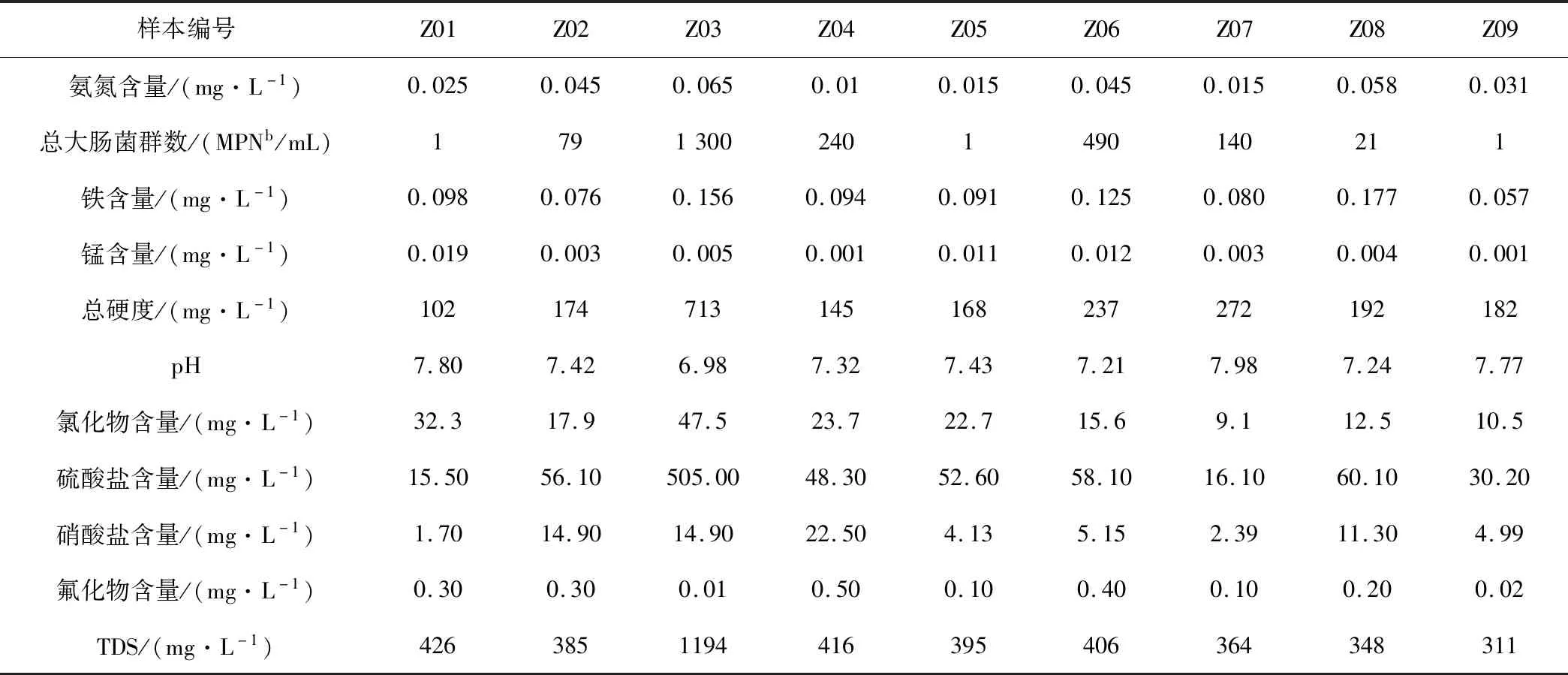
表3 水质检测结果

表4 各指标权重

2.2 计算样本的尼梅罗污染指数

为了突出改进尼梅罗指数法和传统尼梅罗指数法的差异，将改进前后的水质评价结果和F值以图表的形式给出(见图1、表5)。

3 评价分析

研究区域地下水开发利用现状以农村分散居民开采浅层地下水作为生活用水为主，评价范围不涉及地下水集中式饮用水水源保护区，因此根据《地下水质量标准》(GB/T 14848-2017)中的地下水分类，该工程区域地下水环境属Ⅲ类用水。因此，以Ⅲ类水标准来衡量检测结果是否超标。

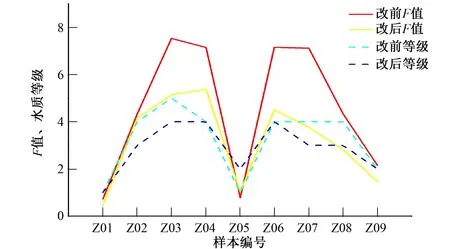
图1 尼梅罗指数法改进前后结果

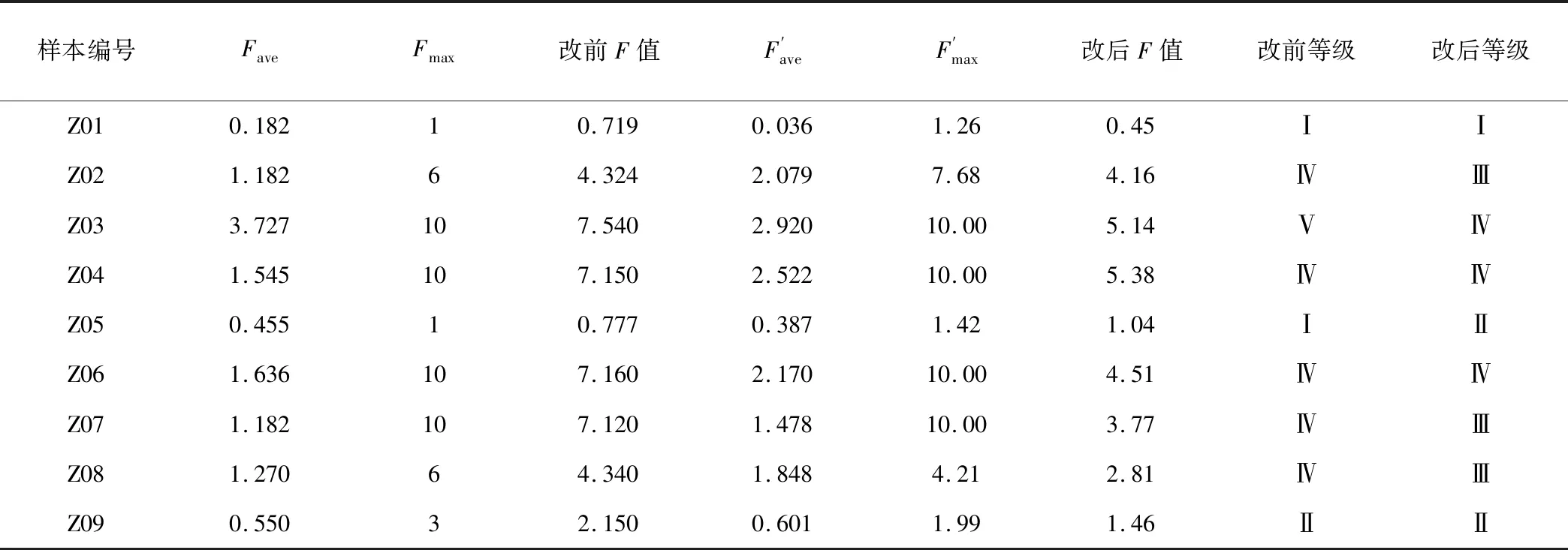
表5 尼梅罗指数法修正前后F值及评价结果对比

通过分析比较可知，除总大肠菌群、总硬度、硫酸盐、硝酸盐、TDS外，其余各项评价指标均未超标。总大肠菌群的超标率最高，达到67%，原因是水质观测点基本分布在农村，卫生条件相对较差，井口周边隔污措施少，富含微生物的生活污水和农田灌溉水渗入井内导致水体污染。总硬度、硫酸盐、硝酸盐、TDS等指标个别超标与区内的生活和农业活动有关。

从表4可以发现，熵权法得到的权重因只考虑客观数据而比较均匀(0.06～0.18)；而二项系数法因为考虑了数据间的联系和实际重要程度而导致权重波动幅度较大(0.001～0.246)；组合赋权同时考虑了2者的优点，更客观地反映样本的综合质量情况。

分析表5可以发现：修正前的水质结果有Ⅰ、Ⅱ、Ⅳ、Ⅴ 4个类别，Ⅰ类2个，约占总数的22%，Ⅱ类、Ⅴ类各1个，分别占总数的11%，缺少Ⅲ类水，以Ⅳ类水为主(5个)，约占总数的56%，水质评价结果偏差；修正后的水质结果有Ⅰ、Ⅱ、Ⅲ、Ⅳ 4个类别，Ⅰ类1个，约占总数的11%，Ⅱ类2个，约占总数的22%，Ⅲ、Ⅳ类各3个，约分别占总数的33%，水质评价结果偏好，且水质级别的分布更加均匀，不再集中于某一类水上。

修正前由于Fi是取的间断值0、1、3、6、10，所以导致最后的F值也是间断分布，且集中在0.71～0.8，4.32～4.34，7.10～7.60这3个狭窄的区间，因此缺乏Ⅲ类水；修正后的F值分布连续，在Ⅰ～Ⅳ类水对应的区间都有分布，且由于考虑了最大权重指标，相对降低了Fmax的贡献，使得F值减小。

4 结 论

地下水质量多指标综合评价的目的是旨在以简便的方法得出精确的结果。传统尼梅罗指数法正是因为评价过程简单、计算简便、物理逻辑清晰才受到广大生产工作者的青睐，但由于Fi不连续以及过分突出Fmax的作用，导致评定结果不是十分合理。因此本文采用Fi连续公式和熵权与二项系数组合权重来改进传统方法，并得到如下结论。

(1)总大肠菌群数量是影响所测样本水质的主要因素，主要原因是生活污水和农业施肥、灌溉。

(2)采用组合赋权的方法能有效规避或削弱单一赋权带来的缺陷并综合2者的优点，这也是涉及多指标赋权问题的一个趋势。

(3)从上述分析结果来看，改进的尼梅罗指数法解决了Fi不连续和过分突出最大值Fmax的问题，使水质评定结果更加连续、均匀。

(4)与传统尼梅罗指数法相比，改进的尼梅罗指数法计算步骤稍多，但计算方法依旧简单。根据《川西气田产能建设项目地下水环评报告》的水质评价结果和实际调查经历，改进的尼梅罗指数法得出的水质评价结果更加符合实际情况。