浅谈导数在经济分析中的应用

江显英

(贵州省黔南民族职业技术学院 贵州 黔南 558000)

随着市场经济的发展，经济的不断繁荣，经济活动中的实际问题将会愈加复杂，企业管理者对经济分析的难度也随之增大，简单的分析已经不能满足企业管理者对经济分析的需求。为了解决这类问题，本文利用常用的经济函数，结合一些实际问题，谈谈如何用导数来进行经济活动分析。

1.导数的概念

函数在某一点的导数是一个常数，是函数增量与自变量增量之比的极限，它反映的是函数值随自变量的变化快慢程度，即变化率，也被称为瞬时变化率。

2.最值在经济分析中的应用

在市场竞争中，厂商想要以价格优势抢占市场份额，有时以产品的平均成本最低为目标而控制产量、这是确定平均成本的最小值问题，经营者的目的是为了追求最大利润——利益最大化原则。

如，某旅行社组织海外旅行团，若每团人数不超过30人，飞机票每张收费2000元；若每团人数多于30人，则给予优惠，每增加1人，机票每张减少20元，直至每张机票降到1000元为止，每团乘飞机，旅行社需付给航空公司包机费30000元，问每团人数为多少时，旅行社可以获得最大利润？最大利润是多少？

这是一个关于最优化的问题，要解决这个问题，首先要建立相应的数学模型。目标函数是利润函数，根据题目给定的条件，建立利润与人数之间的函数关系，由于组团人数以30人为界，因此这里需要用分段函数来表示，要想使利润最大，即要求利润函数的最大值，而最大值只能在驻点处取得，因而问题转化为求函数的导数、驻点以及驻点的函数值。

解：设以x表示每团人数，p表示飞机票的价格，因为(2000-1000)/20=50，所以每团人数最多为30+50=80人，因而每张飞机票的价格

旅行社的利润函数L(x)为：

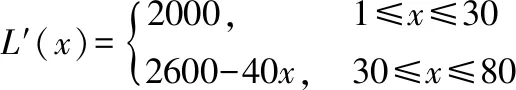
所以，当L′(x)=0，即x=65人时，利润函数取得最大值，即每团65人时，旅行社可以获得最大利润，最大利润是L(65)=54500(元)

3.弹性在经济分析中的应用

边际分析中考虑的函数增量与函数变化率是绝对增量与绝对变化率。实际上，仅仅研究函数的绝对增量与绝对变化率是不够的。例如商品甲每单位产品价格为10元，涨价1元；商品乙每单位产品价格为1000元，也涨价1元，此时两种商品价格的绝对增量都是1元，当与其原价格相比，两者涨价的百分比却有很大的不同，商品甲涨了10%，而商品乙涨了0.1%，由于两者的涨幅差别较大，解决此类问题的有力工具无疑是函数的相对变化率——弹性。

下面列举有关弹性的案例：

案例：有人说：气候不好对农民不利，理由是农作物歉收，会减少农民的收入。又有人说，气候不好反而对农民有利，理由是农作物歉收后其价格会上涨，因而会增加农民收入。应用经济学原理对这两种说法可进行如下解释。气候不好对农民是否有利，关键要看农民的总收入受气候影响如何变动。显然，气候不好的直接影响是农作物歉收，即农产品的供给量减少，这表现为农产品供给曲线将向左上方移动。假设此时市场对农产品的需求量不发生变化，即需求曲线固定不动，那么农产品供给量减少将导致均衡价格上升。由于一般对农产品的需求缺乏弹性，根据需求的价格弹性与销售总收入之间的关系可知，此时农民的总收入将随着均衡价格的上升而增加。故在需求状况不因气候不好发生变化，并且对农产品需求缺乏弹性的情况下，气候不好导致的农业歉收对农民增加收入是有利的。但是，若需求量也同时发生变化或需求是富有弹性，农民将不会因气候不好而得到更多收入。由上述分析可知，对这一问题的回答应该首先对农产品的需求弹性及需求状况做出假定，而不能笼统地下判断。