用户侧电池储能系统的成本效益及投资风险分析
潘福荣, 张建赟, 周子旺, 张 兴, 郑旭初
(1. 国网浙江省电力有限公司宁波供电公司, 浙江 宁波 315000;2. 浙江优能电力设计有限公司, 浙江 宁波 315100)
0 引言
储能系统按照安装位置的不同, 可分为发电侧储能、 输配电侧储能和用户侧储能, 相对前两者, 用户侧储能系统的单体项目相对更小, 也更接近电力用户。 截至2017 年底, 用户侧储能占全部应用规模的27%, 其中工商业削峰填谷占用户侧储能的73%, 是目前中国唯一进入商业化运行的电池储能领域[1]。
当前, 已有相关文献对用户侧储能的经济性进行了研究[2-13]。 文献[2]通过分析与计算, 确定了储能产品的目标成本, 分析了降低成本的主要途径。 文献[3-7]在成本方面只考虑了投资成本和年运行维护费用, 没有考虑置换成本、 废弃处置成本。 文献[3]考虑了用户侧电池储能系统在减少用户配电站建设容量和降低购电费用方面为用户带来的经济价值, 对上海地区某企业安装的钠硫电池储能系统进行了分析, 但没有定量分析各影响因素对储能经济性的影响。 文献[4]虽然考虑了储能系统在减少电网扩建容量、 削峰填谷降低总网损成本、 低储高发套利、 作为新能源发电备用容量和提高可靠性效益5 个主要方面的经济价值,但没有区分利益主体。 文献[5]建立了包括发电侧、 电网侧、 用户侧以及政府补贴的储能电站收益计算模型, 但用户侧经济效益只考虑了减少电量电费。 文献[6]建立了评价储能系统投资经济性的数学模型, 但只从削峰填谷方面分析了储能系统的效益。 文献[7]结合大型企业用户对电能质量和用电可靠性的需求, 对配置柴油发电机和电池储能进行了成本/效益分析。 文献[10]分析负荷侧电池储能系统在延缓设备投资收益、 直接收益、环境效益、 政府补贴4 个方面的经济价值, 但成本方面也只考虑了投资成本和运行维护成本。 文献[11]提出了适用于不同类型电池储能的全寿命周期成本模型, 但没有区分不同用户类型, 没有考虑市场经济环境对用户侧电池储能年均成本的影响。 文献[13]分析了储能在不同应用领域的价值收益模式, 初步建立了储能在不同收益模式下的收益模型, 但没有针对用户侧储能进行分析。文献[16]分析了储能系统在用户侧的应用模式和经济效益, 但没有进行定量计算。
由以上分析可知, 当前对用户侧储能的研究存在以下问题: 储能系统的成本收益模型考虑不全面, 成本收益模型针对多个效益主体, 没有对用户进行细分, 没有定量分析其投资风险。
本文建立了储能全寿命周期成本模型和用户侧收益模型, 基于浙江两部制电价及分时电价政策, 考虑不同的充放电策略, 以不同类型的工商业用户储能项目为例, 对储能项目的经济性进行计算, 并采用Crystal Ball 软件对投资风险进行了评估。
1 用户侧储能系统成本收益模型
1.1 全寿命周期成本模型
各类蓄电池储能的成本结构相同, 全寿命周期成本包括初始投资成本、 运行维护成本、 置换成本和退役成本。
(1)初始投资成本
储能系统主要包括电池组、 PCS(功率变换系统)、 BMS(电池管理系统)、 监控系统等。 初始投资费用主要与系统的存储容量和传输功率有关[2],初设投资成本计算公式如下:

式中: C1为储能系统初始投资成本; Pes为储能系统额定功率; Qes为储能系统容量; kp为与储能系统输入、 输出的峰值功率相关的成本系数; kq为与储能系统容量相关的成本系数。
(2)年运行维护费用
储能系统的年运行维护成本包括储能系统运行成本和维护成本, 主要是电池日常、 定期的人工维护, 如电池及其管理系统故障预防及消除、电池定期人工巡检等。 年运行维护成本可根据式(2)计算[14]:

式中: C2为储能系统运行维护成本; kom为单位容量年运行维护成本系数。
(3)置换费用
当电池储能寿命周期小于实际项目周期时,需对其进行更换, 置换费用主要来源于电池本体。电池储能的置换成本为:

式中: C3为电池每次置换成本; α 为电池成本的年均下降比例;k 为电池更换次数;n 为电池寿命。
(4)废弃处置成本
废弃处置成本指储能设备的寿命周期结束后,为处理该设备所需支付的费用, 主要包括设备残值和环保费用支出两方面。 设备残值与初始投资成本和回收系数有关, 为负值; 环保费用支出主要指回收电池所付出的成本。
随着电池储能回收机制的建立和日益完善,回收价值对电池储能的经济性影响越来越大。 对铅炭电池来说, 随着铅回收技术的进一步提升,目前铅炭电池可实现100%回收, 设备残值可达到初始投资的20%。 废锂电池的处理, 首先要对其进行放电、 拆解、 粉碎、 分选, 拆解之后的塑料以及铁外壳可以回收, 然后再对电极材料进行碱浸出、 酸浸出, 多种程序之后再进行萃取。 锂电池的回收技术复杂, 成本高昂, 目前尚无很好的回收方案, 没有明确的回收价值, 设备残值可看作零。 环保费用支出目前无相关数据参考, 暂不考虑。

式中: C4为储能系统废弃处置成本; γ 为储能系统回收系数。
1.2 收益模型
1.2.1 减少变压器容量投资
采用专用变压器(简称“专变”)供电的工商业用户, 根据自身最大负荷确定专变容量, 考虑建设储能系统, 则可减少专变容量投资。


式中: E1为减少变压器容量而节省的费用; ptr为专变单位容量造价; ST为没有储能时的变压器规划容量;为增加储能后的变压器规划容量; Pmax为不安装储能装置时用户最大计算负荷。
1.2.2 减少电费收益
(1)减少基本电费
采用两部制电价的工商业用户, 基本电价按变压器容量或最大需量计费。 对于新投产用户,考虑安装储能系统, 则变压器规划容量可适当降低, 利用储能的削峰填谷作用可减小用户的最大需量, 也就相应减少了用户每月所交纳基本电费。
基本电价按变压器容量计费时, 则每年减少基本电费E2为:

式中: eT为按变压器容量收取的基本电价。
基本电价按最大需量计费, 则每年减少基本电费E2为:

式中: ees为按最大需量收取的基本电价。(2)减少电量电费
在分时电价机制下, 用户通过储能系统在低谷电价时段充电, 在高峰、 尖峰电价时段放电,从而实现峰谷差套利, 减少购电费用。
每年价差收益E3为:
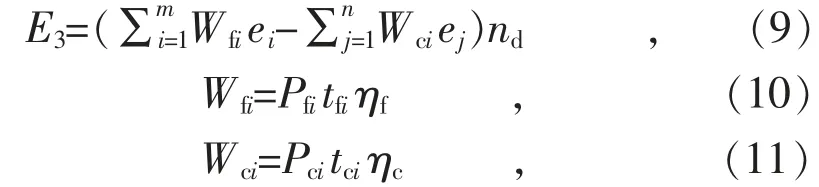
式中: m 为一天内m 个放电时段; n 为一天内n个充电时段; Wfi为第i 个放电时段放电电量; ei为第i 个放电时段用户用电电价; Wci为第i 个充电时段充电电量; ej为第j 个充电时段用户用电电价; nd为储能系统年平均运行天数; Pfi为第i个放电时段放电功率; Pci为第i 个充电时段充电功率; tfi为第i 个放电时段放电时长; tci为第i 个充电时段充电时长; ηf为平均放电效率; ηc为平均充电效率。
1.2.3 降损收益
储能系统的削峰填谷作用可减少专变损耗和用户配电网络损耗。 由文献[15]可推导, 在负荷功率因数和负荷点电压不变的情况下, 2 条负荷曲线所引起的有功损耗之差为:

式中: ΔW 为2 条负荷曲线在一天内的有功损耗之差; R 为用户变压器和用户配电网络电阻之和; cosθ 为负荷功率因数; U 为负荷母线电压; f1(t)为无储能系统时, 用户负荷曲线在t 时刻负荷值; f2(t)为建设储能系统后, 用户负荷曲线在t时刻负荷值; E4为年降损收益; eav为峰谷电价平均值。
1.2.4 可靠性收益
电力用户停电初期损失包括可能的设备损坏、
出现残次品、 少生产产品的利润损失与恢复生产启动费用等, 停电持续一定时间后, 停电损失主要是少生产产品的利润损失。 为避免过充过放影响电池寿命, 化学储能系统的DOD(放电深度)一般不超过80%, SOC(剩余电量)通常在20%以上,可以作为用户的后备电源。
停电损失与负荷重要程度、 行业类别、 停电时间、 停电时长、 失负荷大小等因素有关。 储能系统的配置对单回路、 双回路供电模式的可靠性有较大提升, 尤其是对于单回路供电模式, 而对双电源供电模式的可靠性几乎无提升效果[16]。
采用以下公式对可靠性收益进行计算:

式中: E5为用户建设储能系统后, 由供电可靠性提高带来的收益; Δr 为用户单位容量停电1 h 的损失; Δt 为建设储能系统后, 将减少的停电负荷折算到储能系统额定功率后的年平均停电时间。
2 用户侧储能系统经济性分析及风险评估
2.1 经济评价指标
考虑资金时间价值, 利用动态投资回收期、NPV(净现值)、 IRR(内部收益率)3 个经济评价指标对用户侧储能项目进行经济性评价。
(1)动态投资回收期(Pt′)计算

式中: CI 为现金流入量; CO 为现金流出量; i0为基准收益率; Pt′为动态投资回收期。(2)NPV 计算
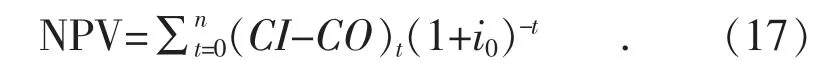
若NPV≥0, 则说明该方案能满足基准收益率要求的盈利水平且还能得到超额收益, 故方案可行。
(3)IRR 计算

若IRR≥ic(预期收益率), 则NPV>0, 说明项目在经济效果上可行。
2.2 生命周期内NPV
在储能系统的一个生命周期内, NPV 为:

式中: ET为储能系统生命周期内收益净现值; CT为储能系统生命周期内成本净现值; CPA(i, n)为年金现值系数; CPF(i, n)为一次支付现值系数。
2.3 投资收益及投资风险分析
由NPV 计算公式可知, 影响储能系统经济性的因素有: 储能系统额定功率、 储能系统容量、单位容量成本、 单位功率成本、 寿命、 电池回收系数、 基本电价、 峰谷电价、 储能系统年平均运行天数、 用户单位容量单位时间停电损失等。
随着技术的进步, 储能系统单位容量成本、单位功率成本会逐渐下降, 电池寿命也会逐渐增长, 同时峰谷电价、 基本电价等政策变动也会给储能项目投资带来风险, 在投资决策时需定量评估这些风险。
储能项目经济指标计算流程如图1 所示。 本文基于储能系统成本收益模型, 通过识别风险因素, 采用Crystal Ball 软件进行投资收益及投资风险分析。

图1 储能项目经济指标计算流程
3 算例分析
3.1 基础数据
2018 年9 月1 日浙江省工商业用户电网销售电价见表1。 可见, 浙江工业用户峰谷电价差为0.633~0.666 元/kWh, 一般商业用户峰谷电价差在0.796~0.828 元/kWh。
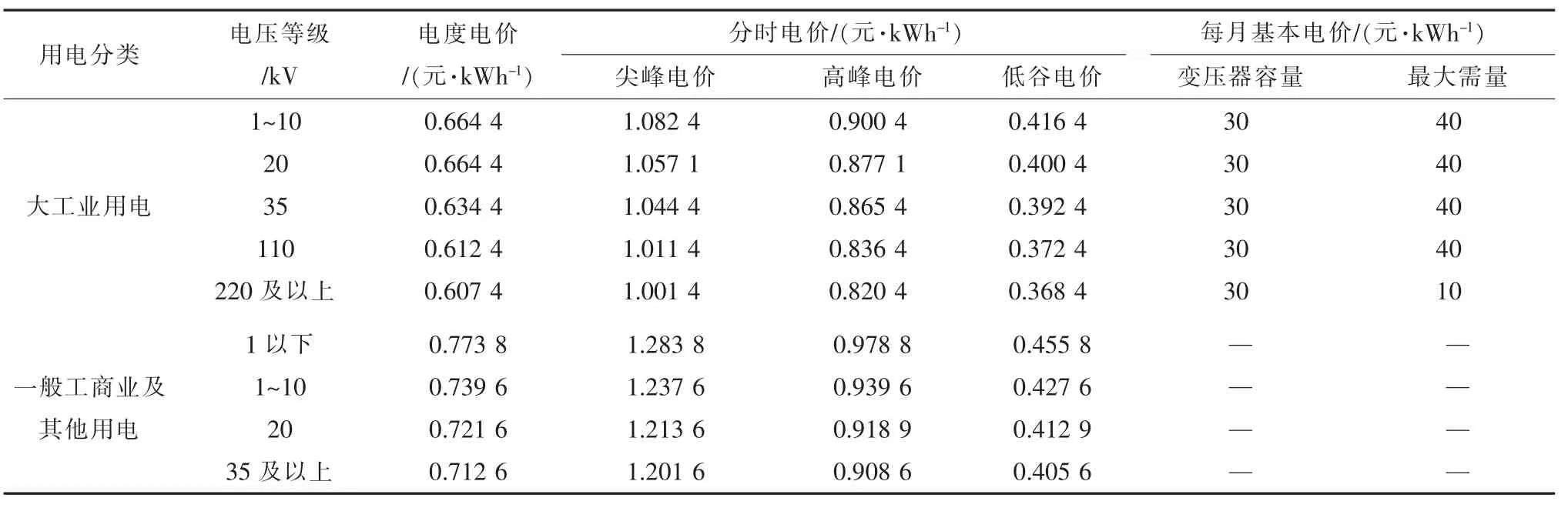
表1 浙江省工商业峰谷电价
分时电价时段划分见图2: 尖峰时段为19:00-21:00; 高峰时段为8:00-11:00, 13:00-19:00,21:00-22:00; 低谷时段为11:00-13:00, 22:00-次日8:00。

图2 浙江工商业六时段分时电价
从各种储能电池性能比较来看, 锂电池与铅蓄电池由于产业化基础较好, 相比其他路线具有明显的成本优势, 本文针对铅蓄电池、 磷酸铁锂电池进行分析。 2 种电池技术性能参数见表2。

表2 电池技术性能参数
3.2 投资收益计算
(1)大工业用户
以10 kV 大工业用户建设100 kW 的储能系统为例, 在浙江当前充放电条件下, 采取低谷充电、 尖峰放电, 在充放电时长各为2 h 时收益最大, 计算结果见表3。
由表3 计算结果可知, 在浙江当前的峰谷电价条件下, 10 kV 大工业用户建设磷酸铁锂电池、铅炭电池储能均能实现盈利。
(2)一般工商业用户
以10 kV 一般工商业用户建设100 kW 储能系统为例, 在浙江当前充放电条件下, 采取低谷充电、 尖峰放电, 在充放电时长各为2 h 时收益最大, 计算结果见表4。
由表4 计算结果可知, 在浙江当前的峰谷电价条件下, 由于缺少基本电费收益, 10 kV 一般工商业用户建设磷酸铁锂电池储能无法盈利, 铅炭电池储能可勉强实现盈利, 内部收益率为4.23%。
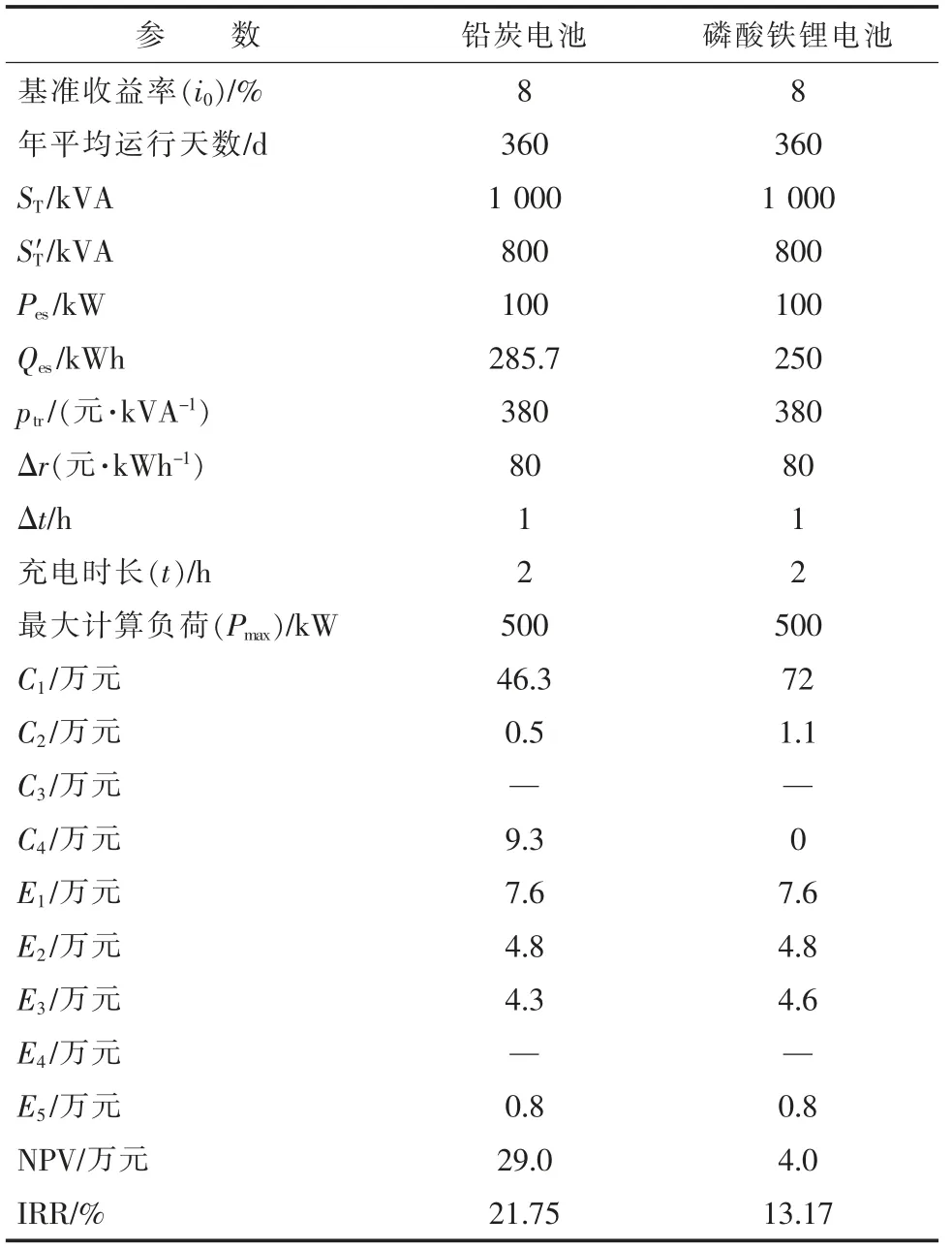
表3 10 kV 大工业用户储能系统投资收益

表4 10 kV 一般工商业用户储能系统投资收益
3.3 投资风险分析
考虑各种影响因素的不确定性, 分析大工业用户储能项目投资风险。 各假设变量的分布和决策变量取值范围见表5, 其中N(μ, σ2)表示变量服从正态分布。

表5 假设变量分布及决策变量范围
采用蒙特卡洛模拟10 000 次, 得到铅碳电池NPV 概率分布如图3 所示, 可以看出, 铅碳电池NPV 最小值为19.09 万元, 最大值为37.19 万元, 平均值28.92 万元。 按大小对影响净现值的因素进行排序, 得到项目周期、 单位容量成本、回收系数、 系统平均运行天数、 单位功率成本、能量转换效率等因素的敏感度数据如表6 所示,可以看出, 项目周期和单位容量成本对效益的影响占90%以上。
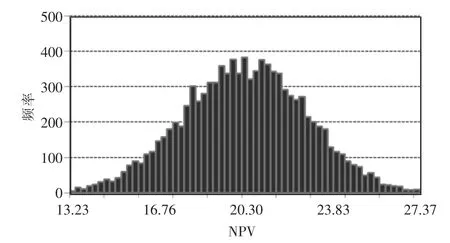
图3 铅碳电池NPV 概率分布

表6 铅碳电池NPV 敏感度数据
采用蒙特卡洛模拟10 000 次, 得到磷酸铁锂电池NPV 概率分布如图4 所示, 可以看出, 磷酸铁锂电池NPV 最小值为-3.55 万元, 最大值为11.71 万元, 平均值3.80 万元, NPV>0 的概率为96.51%。 按大小对影响NPV 的因素进行排序, 得到项目周期、 单位容量成本、 年运行天数、 能量转换效率、 单位功率成本的敏感度数据见表7。

图4 磷酸铁锂电池净现值概率分布

表7 磷酸铁锂电池NPV 敏感度数据
4 结语
本文建立了用户侧储能系统成本收益模型,利用NPV、 IRR 等经济评价指标对浙江大工业用户、 一般工商业用户储能案例进行了效益分析。在当前浙江峰谷电价及两部制电价下, 大工业用户采用铅炭电池和磷酸铁锂电池的IRR 分别能达到21.75%和13.17%, 具有不错的经济性。 一般工商业用户由于缺少基本电费收益, 采用铅炭电池可勉强实现正收益, IRR 为4.23%; 采用磷酸铁锂电池, 目前还不具备经济性。 最后, 采用Crystal Ball 软件对大工业用户的储能项目进行敏感度分析、 投资风险计算, 为浙江开展用户侧储能项目提供指导。

