变压器绕组匝间短路电动力的研究

关羡滨，滕 跃，张洪坤，鲍 峰，张秀红

[1.松花江水力发电有限公司吉林白山发电厂，吉林省吉林市 132013；2.华润电力（锦州）有限公司，辽宁省锦州市 121006]

0 引言

变压器绕组匝间短路故障具有检测困难、电动力剧烈和危害大等特点[1]。变压器故障的统计资料显示，由于匝间短路故障辨识难度大导致变压器设备损坏的比重较高[2]。差动保护作为变压器的主保护，在处理该故障时存在失效或拒动的问题，从而导致长期负载运行的绕组出现严重变形、绝缘损坏等恶劣后果[3]。

短路电抗法、频率响应法和低压脉冲法等作为变压器绕组形变的传统检测方法，在检测过程中具有运输困难、试验费用昂贵、接线复杂以及耗时长等缺点，已经不适用快速发展的电力系统[4]。机械振动法作为在线监测法中的一种，具有操作简单、对设备影响小以及费用低等优点，能够安全可靠地监测设备的运行状态，具有较好的应用前景[4]。变压器绕组短路故障时电流激增以及受力剧烈，是变压器绕组振动的主要原因，因此对变压器绕组电动力的研究有助于分析变压器绕组的振动与形变特性。近年很多学者基于场路耦合原理研究变压器内部故障时磁场问题[5]。文献[6]利用有限元法研究变压器的直流偏磁效应，虽然考虑了变压器故障时的电磁特性，但是二维模型的计算误差较大。国内外已有文献研究变压器绕组外部短路时的电动力，通过对比二维和三维仿真模型下的短路电动力，说明三维电磁模型更具有适用性[7]。文献[8]利用有限元法仿真分析短路绕组的轴向和径向电动力，但是没能考虑安匝不平衡对绕组电动力的影响。已有研究表明，变压器绕组匝间短路对设备运行乃至系统稳定产生了极大危害，虽然这一问题引起了国内外的广泛关注，但是罕有文献对变压器绕组匝间短路电动力进行分析。

本文基于场路耦合原理，提出一种变压器绕组匝间短路电动力分析方法。通过建立变压器三维有限元磁场模型，模拟绕组匝间短路故障时谐电磁环境，结合时域微分电路模型分析变压器故障时绕组电磁力的变化情况，并总结其规律。最后，通过对比数值仿真与物理实验验证仿真模型的正确性和有效性。

1 变压器绕组匝间短路仿真模型

变压器绕组作为多自由度机械系统，变压器绕组的电动力使用虚位移法[9]计算：

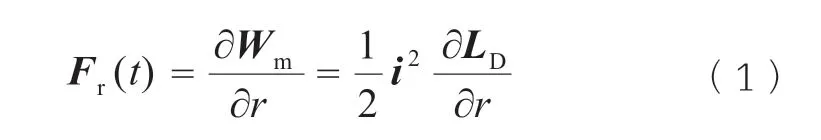
式中Fr——作用在r方向的电磁力；

Wm——绕组漏磁场的磁场储能；

i和LD——基于场路耦合计算得到的绕组电流和电感。

基于变压器时域场路耦合电磁仿真模型进行绕组匝间短路电动力分析，由式（1）可知动态电感和时域电流为绕组电动力关键的电磁耦合参数，其中等效电路模型计算时域电流，三维等效磁场模型计算动态电感。

1.1 磁场模型

基于磁场模型分析变压器励磁非线性问题，采用棱边有限元法以及矢量磁位A，建立变压器磁场模型：

式中μ——磁导率，

J——电流密度矢量。

依据棱边有限元法求解模型磁场区域的整体插值函数为：

式中 {Mn，n=1，2，…，nn}——基函数序列，n——序列编号，nl——总棱边数。

依据格林定理对上式求解，可得相应磁场区域的伽辽金加权余量方程：

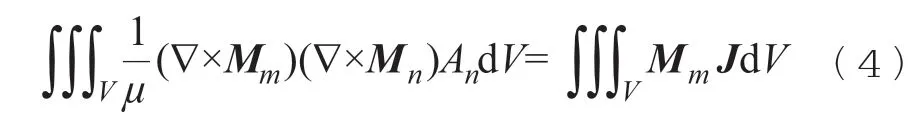
式中 {Mm}——权函数序列，

m——序列编号。

磁场模型中若已知电流i，将加权余量方程离散形成代数方程组，求解可得A，进而计算磁场能量。

1.2 电路模型

变压器磁链方程为：

式中ψ——模型的磁链向量；

Ls（t，i）——静态电感矩阵；

i——电路模型的绕组电流；

利用变压器内部基本电磁关系，可知时域电路微分方程为：

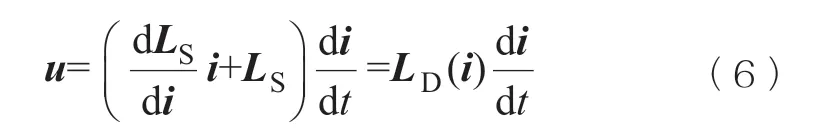
式中u——电压激励；

LD——动态电感矩阵。

若tk时刻的线圈电流为ik，利用四阶龙格库塔法对电路模型中建立的方程求解，可知tk+1时刻的电流ik+1为：

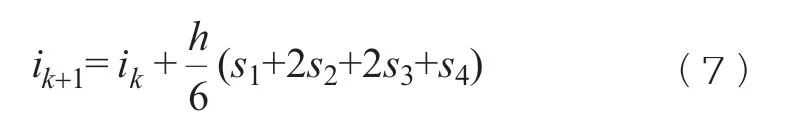
式中h——步长，

s1～s4——步长内的分段计算斜率。

基于能量扰动的思想，若线圈电流增加Δi时，将电源总能量与动态电感和电流关联：

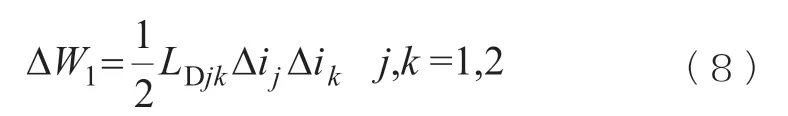
同时，相同电流变化量的条件下，变压器对应内部系统的磁场能量增量为：

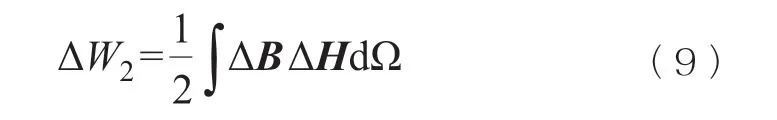
基于变压器能量转换过程中的能量守恒原理，联立式（7）和式（8）可计算动态电感LD。

2 仿真分析

基于场路耦合计算变压器绕组匝间短路电动力。单相三柱式实验变压器参数见表1。

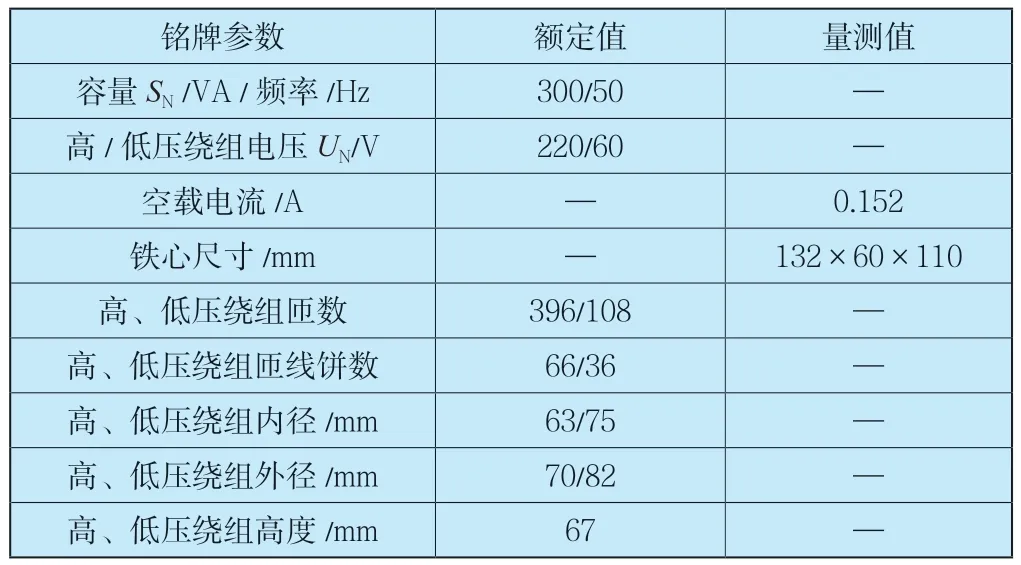
表1 单相变压器额定参数Table 1 Rated parameters of single-phase transformer

磁场模型求解时在外表面施加磁场平行的边界条件，电路模型中施加正弦电压作为激励，依据场路耦合模型分析变压器高压侧绕组匝间短路工况下短路绕组电磁力的变化规律。

利用ANSYS/Maxwell建立变压器三维模型，仿真模型如图1所示。其中，R1和R2分别表示原、副边电阻，ZL为负载，N11、N12和N13为高压绕组，其中N12为短路绕组，N2为低压绕组。

（1）绕组首端匝间短路。

变压器空载运行，高压绕组首端分别设置6%和10%的匝间短路故障，短路线饼分别为1～4号线饼和1～7号线饼。

变压器绕组首端匝间短路时各线饼受力分布见图2。

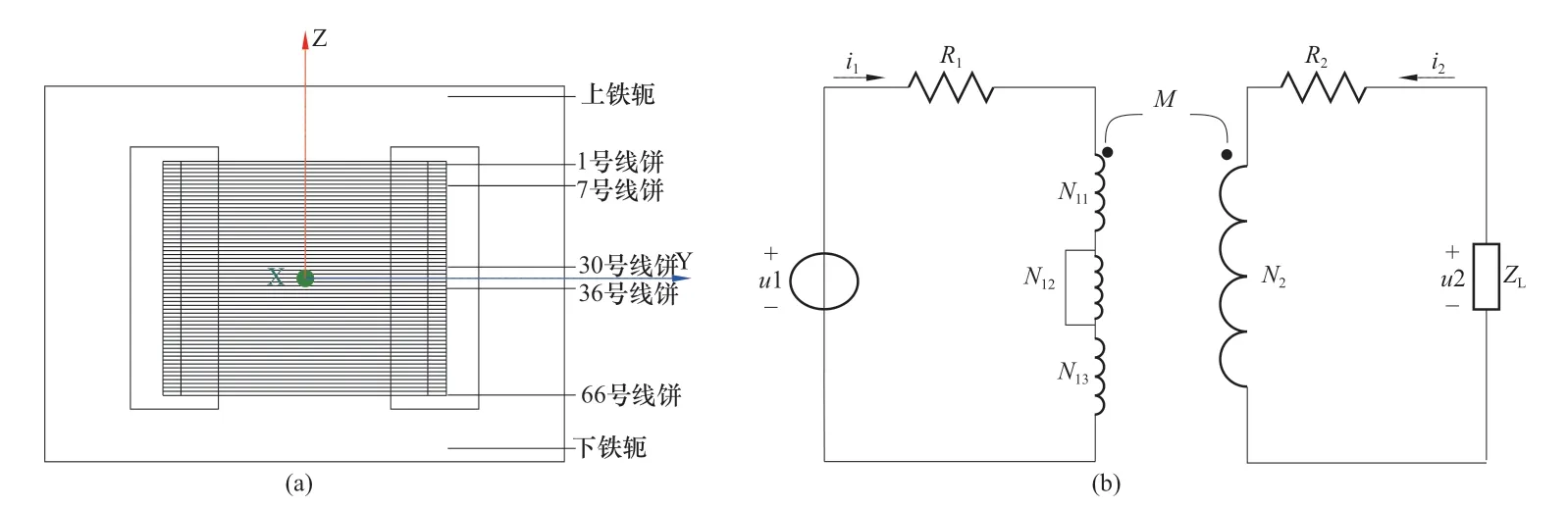
图1 变压器匝间短路仿真模型（a）高压绕组结构；（b）仿真电路图Figure 1 Simulation model of inter-turn short circuit

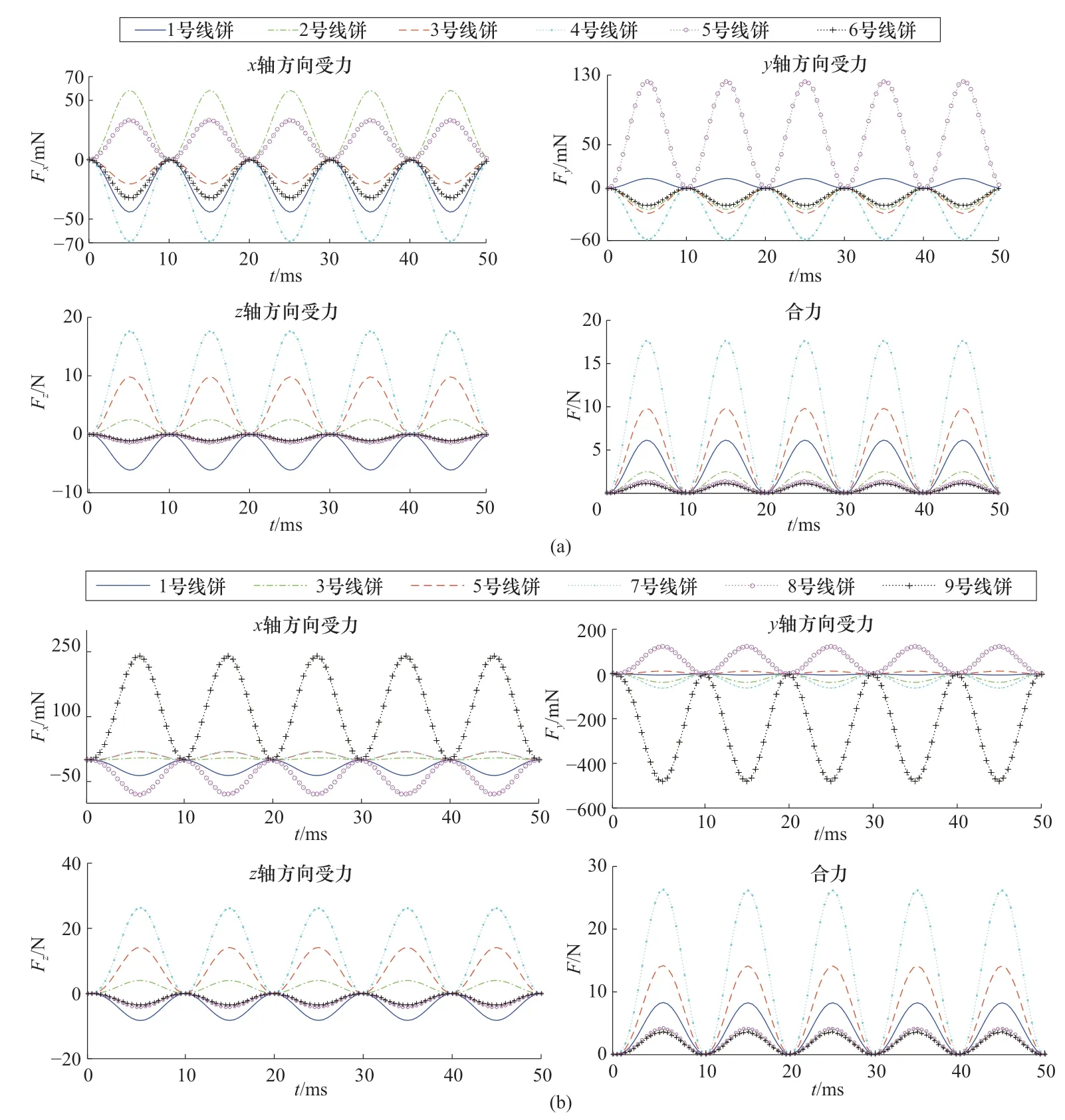
图2 首端绕组电动力分布（a）6%匝间短路；（b）10%匝间短路Figure 2 Force distribution in top winding

由图2可知，由于不同位置线饼的漏磁通方向各异，造成线饼承受不同方向的拉伸或压缩力。短路绕组在径向受力较小，且随着短路匝数的增大，使得非短路绕组沿径向的受力值高于短路绕组。短路绕组以及非短路绕组主要承受轴向电磁力，非短路绕组沿轴向受力小于短路绕组。两种短路状态都表明短路绕组中，远离铁轭的绕组受力值高于靠近铁轭的绕组受力值，且两种绕组沿z轴受力的方向相反。

（2）距离首端1/3处匝间短路。

变压器空载运行，距离高压绕组首端1/3处分别设置6%和10%的匝间短路故障，短路线饼分别为21～24号线饼和1～7号线饼。

距离高压绕组首端1/3处匝间短路时各线饼受力分布见图3。

6%匝间短路时，距离高压绕组首端1/3处的绕组沿径向的受力远小于相同情况时的首端绕组。随着短路匝数的增大，非短路绕组沿径向的受力值高于短路绕组。短路绕组以及非短路绕组主要承受轴向电磁力，非短路绕组沿轴向受力小于短路绕组，且非短路绕组沿轴向的受力具有对称性。

（3）绕组中部匝间短路。

变压器空载运行，高压绕组中部分别设置6%和10%的匝间短路故障，短路线饼为31～34号线饼和30～36号线饼。

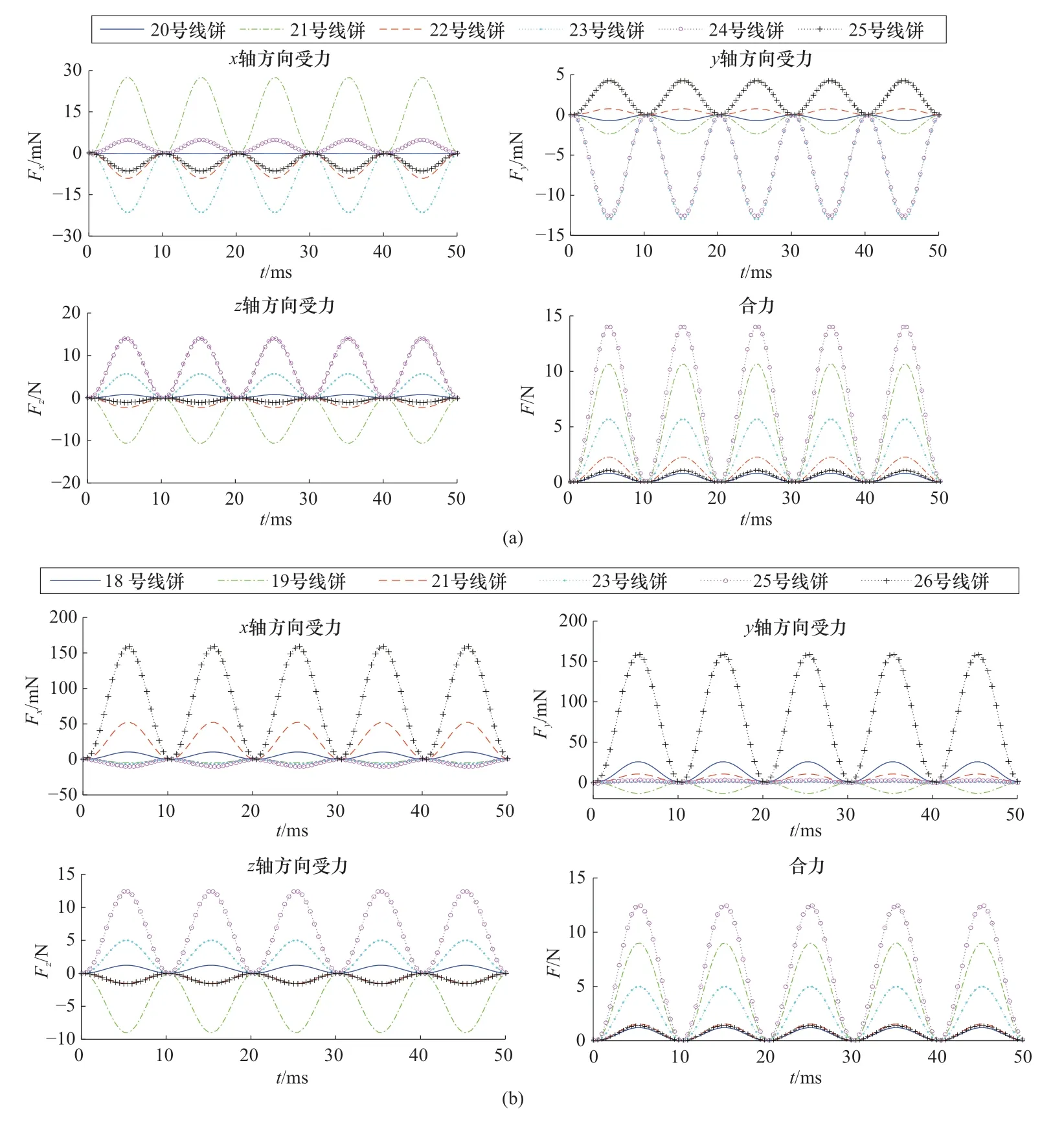
图3 1/3处绕组受力分布图（a）6%匝间短路；（b）10%匝间短路Figure 3 Force distribution in third winding

变压器绕组中部匝间短路时各线饼受力分布见图4。

由图4的可知，中部绕组短路时，随着短路匝数的增多，非短路绕组沿y方向承受应力增加幅度高于沿x方向的受力情况，且受力值前者高于后者。短路绕组以及非短路绕组主要承受轴向的电磁力，短路绕组轴向电磁力高于非短路绕组，合力的最大值分布在短路匝的两端。同时，短路匝两端沿轴向的受力方向相反，且具有对称性。

3 实验验证

绕组振动加速度是电磁力激励下的强迫振动，将首端短路线饼电磁力作为简谐激励源，进行谐响应仿真分析。考虑铁心振动的影响，分别量测铁心与绕组的振动情况，利用盲源分离法[10]获取首端10%匝间短路故障时绕组振动的具体信息，仿真与实验结果如图5所示。

由图5可知，匝间短路时首端绕组振动的仿真与实验量结果具有一致性，且绕组的振动主频为100Hz。仿真与实验的结果表明，该模型能够有效和正确地仿真绕组匝间短路的受力值。

研究表明，通过建立变压器匝间短路电磁模型，开展变压器绕组匝间短路电动力的仿真分析，有助于解决变压器故障时绕组的受力影响，进而预测绕组在短路冲击下的变形情况。

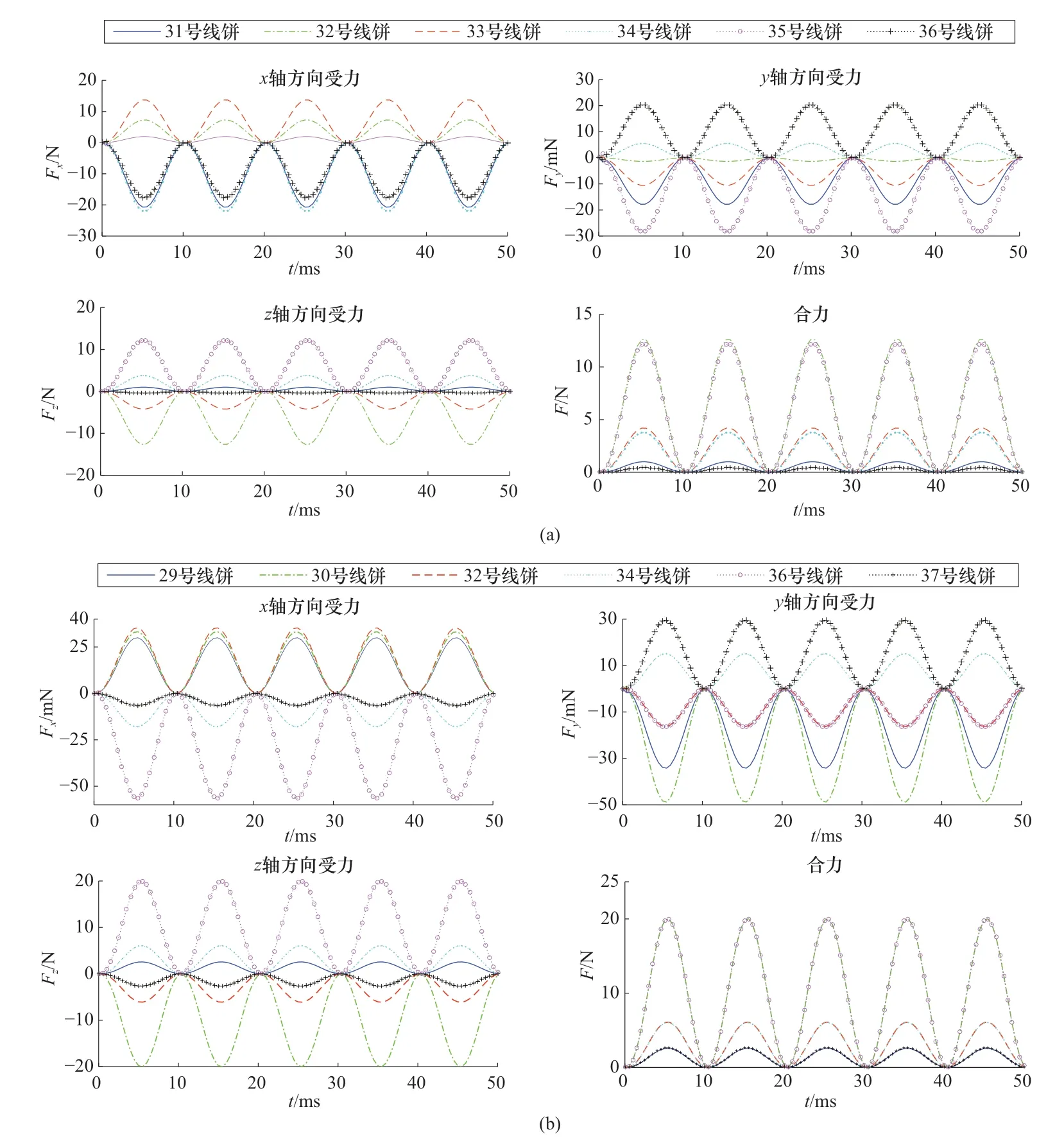
图4 中部绕组受力分布图（a）6%匝间短路；（b）10%匝间短路Figure 4 Force distribution in middle winding

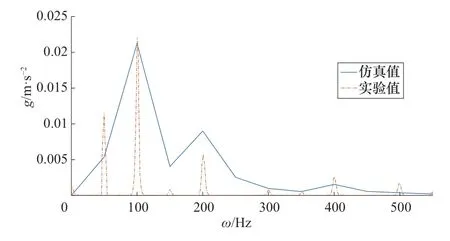
图5 变压器绕组首端振动频谱图Figure 5 Vibration spectrum in top winding

4 结束语

利用时域场路耦合模型研究变压器绕组匝间短路问题，得出以下结论：

（1）绕组在不同位置发生匝间短路时，端部匝间短路所产生的电动力更为恶劣。结果表明场路耦合模型能够有效模拟变压器绕组匝间短路时的内部磁场环境，仿真振动谐响应与振动频谱图对比验证了本文方法的正确性。

（2）电动力仿真结果表明，短路绕组主要承受轴向电磁力，端部绕组匝间短路时，线饼受力较为严重。首端及距离高压绕组首端1/3处绕组匝间短路时，短路电动力不具有对称性，中部匝间短路时，短路电动力具有对称性。