考虑铁耗的异步电机状态观测器设计及关键参数辨识研究
董 侃,刘伟志,马颖涛,宋永丰,安泊晨
(中国铁道科学研究院 机车车辆研究所,北京 100081)
异步电机因其结构简单、易于维护、可在恶劣环境下运行等优点而在传动领域得到广泛应用[1]。异步电机在额定载荷附近能达到较高的效率,然而在列车惰行等轻载工况下的效率并不理想。随着国家大力倡导节能降耗理念,如何解决异步电机的轻载低效问题已成为目前高性能传动控制领域的研究热点。
国内外对异步电机效率优化控制的研究已有近40年时间,在众多方法中[2-3],基于损耗模型的控制方法LMC(Loss Model Control)因其物理意义明确、寻优速度快等优点而得到广泛关注。然而LMC算法的优化效果依赖于准确的电机参数,由于电机运行工况复杂多变,电机参数通常也会大范围变化。因此,要提高优化效果,需要准确实时获得电机参数。
目前,在线辨识技术一般可以分为频域辨识、时域辨识和人工智能法三大类[4]。其中,频域辨识由于不能反映动态过程中的非线性,研究趋于减少。时域辨识中,目前主要有最小二乘法、模型参考自适应法和扩展卡尔曼滤波法,三种方法各有优缺点,其中最小二乘法计算量小,然而对扰动抑制能力较弱[5];扩展卡尔曼滤波法对噪声不敏感,且动态性能较好,然而计算量大[6];模型参考自适应法辨识效果较好,但同时辨识多个参数时,自适应率较难设计[7-8]。人工智能法目前理论研究成果较多,但在大功率交流传动领域的工程应用尚不成熟[9]。
本文在前人研究的基础上,基于稳定性分析设计自适应律,对损耗模型中的关键参数进行自适应辨识研究。设计了考虑铁耗的异步电机状态观测器,为提高观测速度和系统的鲁棒性,进行基于反馈矩阵的极点配置;设计了基于稳定性定律的关键参数自适应辨识算法,改善了算法性能;通过仿真和实验对本文理论进行了验证。
1 基于损耗模型的电机效率优化算法现存问题
基于损耗模型的电机效率优化算法以准确的电机模型为基础,通过优化磁链指令达到电机损耗最小的目的。由文献[10]可知,异步电机损耗模型表达式和优化磁链表达式为
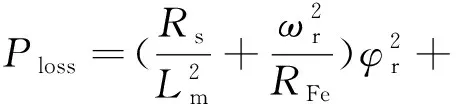
( 1 )
( 2 )
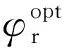
定义电机效率为
( 3 )
式中:ωm为机械角频率。
结合式( 1 )~式( 3 )可得
( 4 )
其中
( 5 )
( 6 )
定义因电机参数偏差而带来的效率变化百分比为
( 7 )
式中:xn为所研究参数的额定值;Δx为参数的偏差值。基于上述推导,得到图1、图2所示定子电阻和铁耗电阻对优化算法的影响。
可见,损耗模型法的优化效果依赖于电机参数,且低速下定子电阻影响较大,铁耗电阻影响较小,高速下铁耗电阻的影响逐渐增大。因此要提高优化效果,需对电机关键参数进行实时修正。
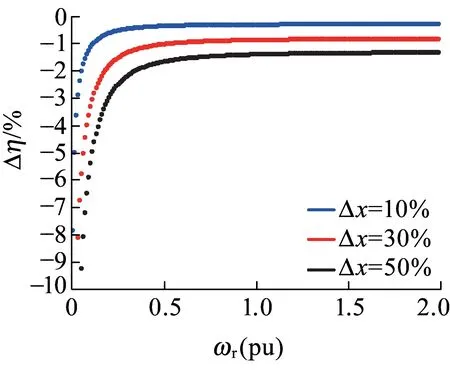
图1 定子电阻参数敏感性
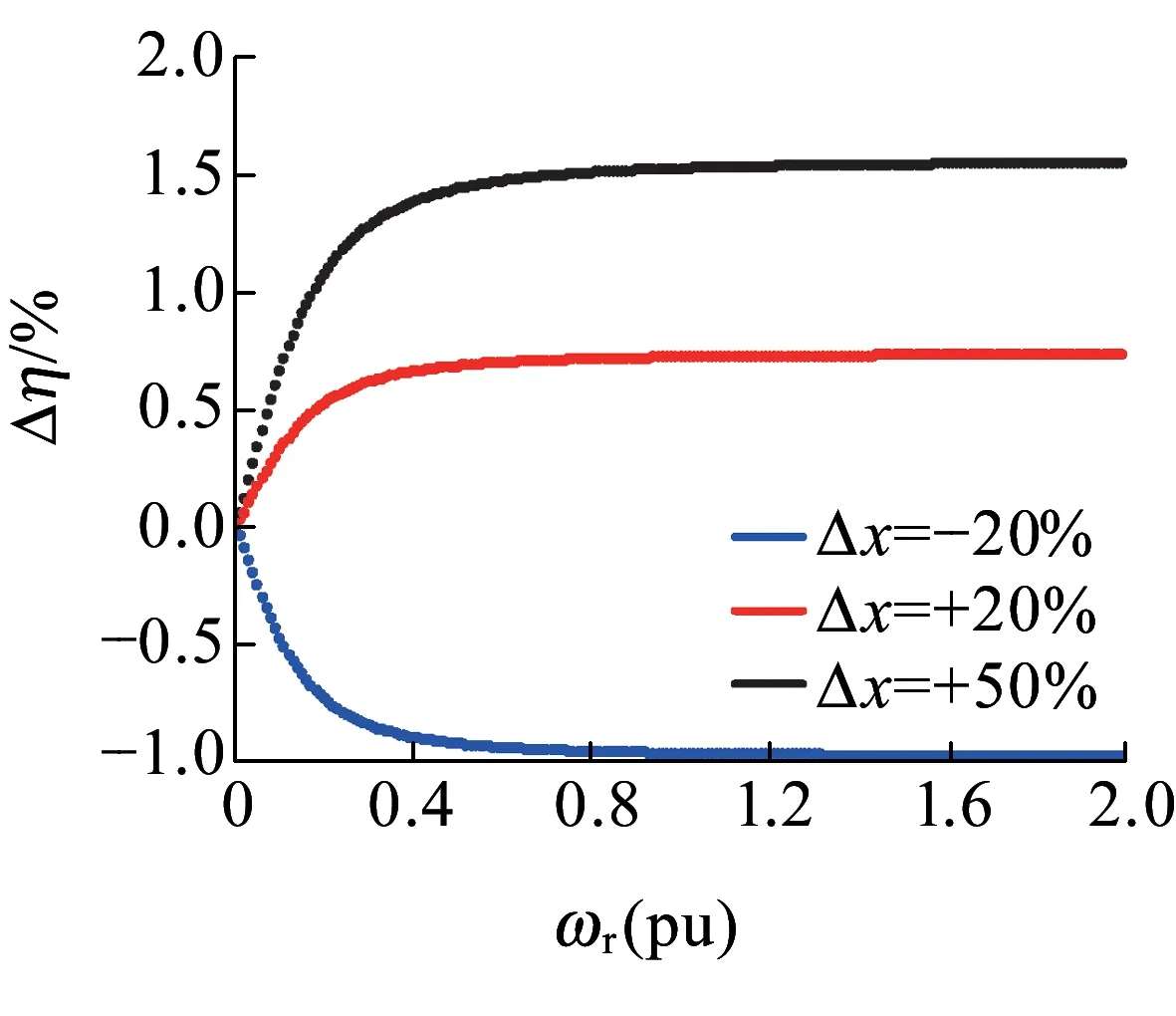
图2 铁耗等效电阻参数敏感性
2 考虑铁耗的状态观测器设计
铁耗是电机运行过程中真实存在的,并且电机损耗模型中包含铁耗参数,而传统的状态观测器通常忽略铁耗的影响。对包含铁耗的状态观测器进行设计,并对闭环观测器进行极点配置。
2.1 考虑铁耗的状态观测器设计
图3为两相静止坐标系下包含铁耗的电机等效电路。其中,ωsl为转差角频率,Isα和Isβ分别为定子α、β轴电流,Irα和Irβ分别为转子α、β轴电流,Vsα和Vsβ分别为定子α、β轴电压,Vrα和Vrβ分别为转子α、β轴电压,φmα和φmβ分别为α、β轴主磁链,iFeα和iFeβ分别为α、β轴铁耗等效绕组电流。
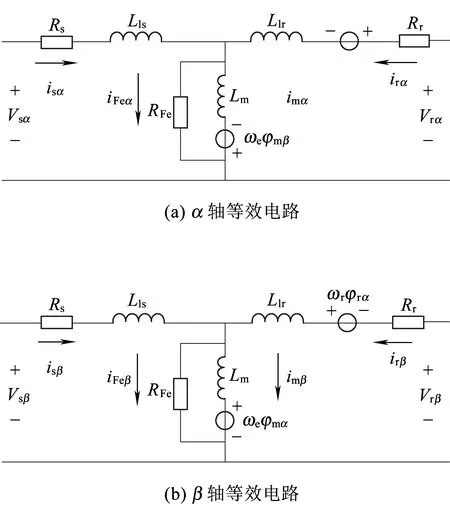
图3 考虑铁耗的电机等效电路
忽略图3暂态过程,由励磁支路电压方程和气隙主磁路方程转子电流可表示为
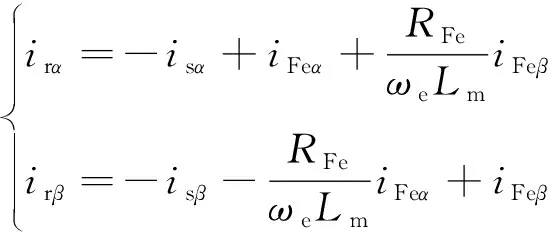
( 8 )
由转子磁链公式转子电流还可表示为
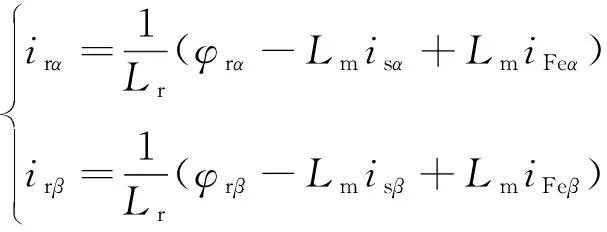
( 9 )
结合式( 8 )、式( 9 )可得铁耗支路电流为
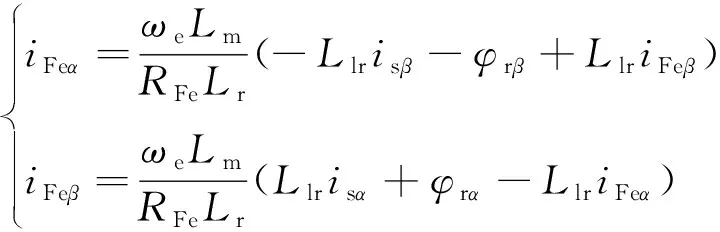
(10)
定义
(11)
(12)
将式( 9 )分别代入定子磁链和转子电压方程,可得
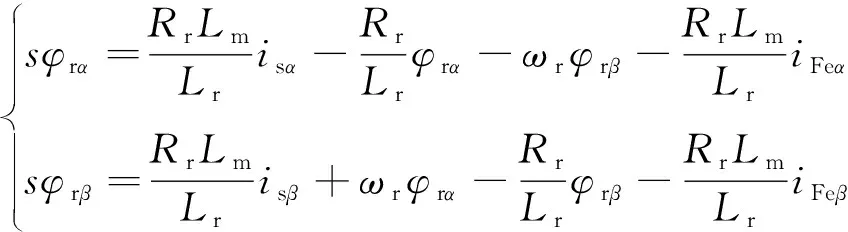
(13)
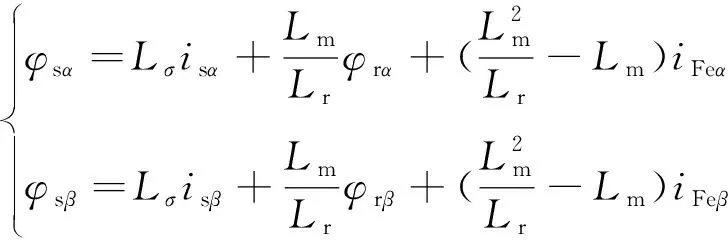
(14)
将式(13)、式(14)代入定子电压方程,并忽略定转子漏感,可得
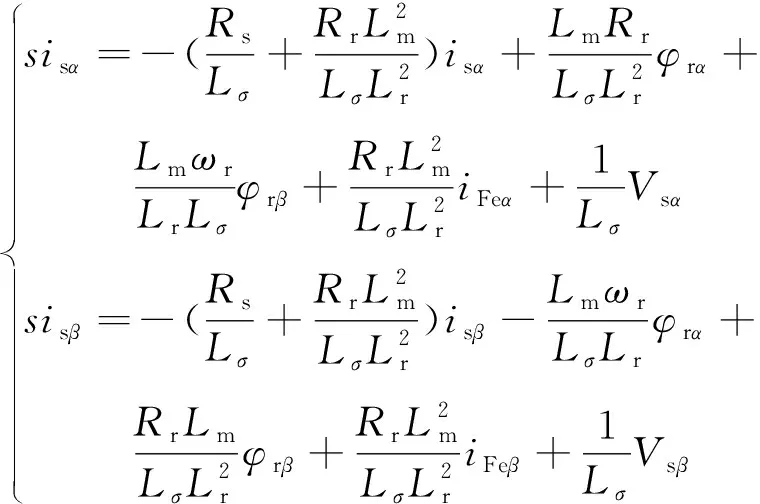
(15)
利用式(10)对式(13)和式(15)中的铁耗支路电流分量进行化简,整理得
(16)
其中
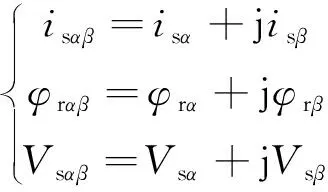
(17)
(18)
(19)
(20)
(21)
(22)
(23)
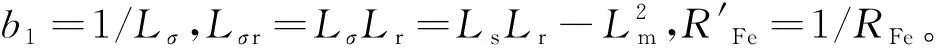
下文对该模型进行闭环极点配置,并基于此对关键参数进行自适应辨识。
2.2 极点配置
由于开环观测器对扰动的抑制能力较差,通常需引入状态反馈矩阵。将开环观测器写成标准形式
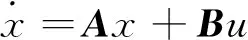
(24)
由于定子电流较易测量,通常以定子电流误差为反馈,通过反馈矩阵K进行极点配置,由此构成的闭环状态观测器如图4所示,其中F=[1 0],C=[0 1]。
闭环观测器的状态方程为
(25)
(26)
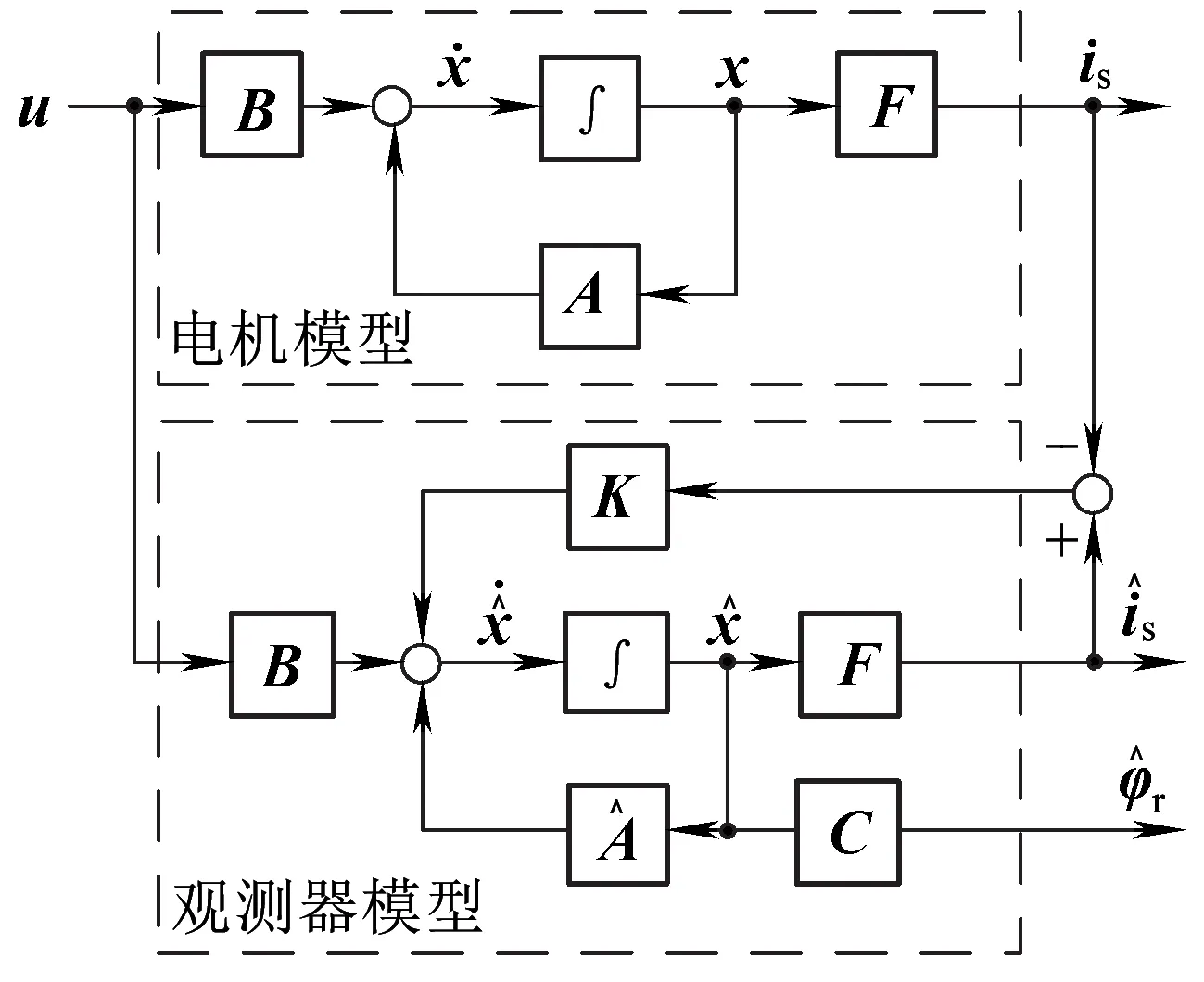
图4 闭环状态观测器
进一步整理式(25)可得
(27)
反馈矩阵K通常可表示为[11]
(28)
则式(27)所示闭环观测器可表示为
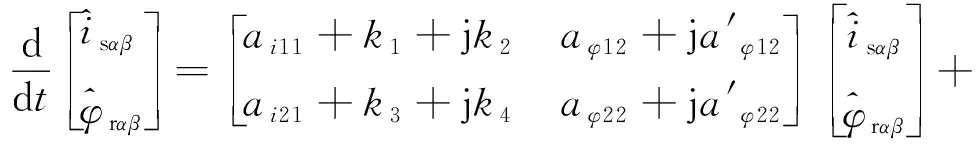
(29)
由控制理论可知,连续系统的极点在复数左半平面即可保证系统稳定,并且极点配置越远离虚轴,系统收敛越快,但对系统扰动的抑制能力也越差。因此需要综合考虑系统收敛速度与对扰动的敏感性进行极点配置[12]。
电机状态观测器的极点配置方式主要有两种:一是将观测器极点配置为与电机极点成正比关系[13],二是将观测器极点的实部配置为与电机极点的实部成正比关系[14]。综合考虑观测器收敛速度、抗干扰能力和数字实现方式等条件,本文将观测器极点配置为电机极点的p倍,考虑到观测器收敛速度应大于电机收敛速度,p应大于1。即
λo=pλm
(30)
式中:λo为所设计的闭环极点;λm为电机模型的极点。
为简化计算,定义
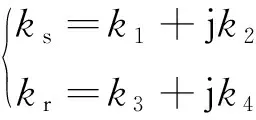
(31)
综合式(16)、式(29)和式(31)推导可得电机模型和观测器模型的特征方程为
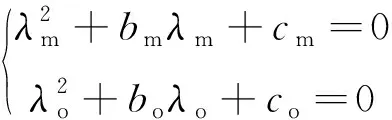
(32)
其中
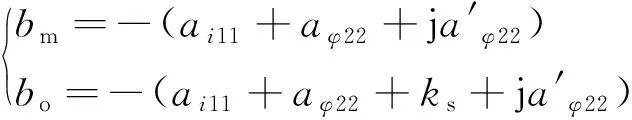
(33)
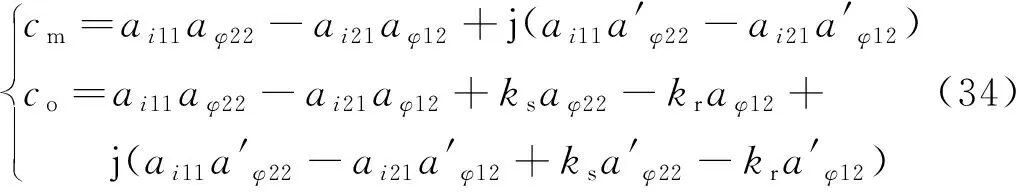
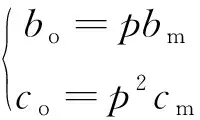
(35)
对式(35)进行求解,可得
(36)
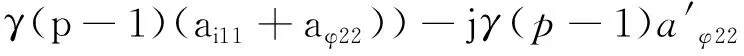
(37)
由上文分析可知,p值越大,观测器极点离虚轴越远,系统收敛越快,但对扰动的抑制能力也越差;反之,p值越小,极点离虚轴越近,系统对扰动的抑制能力增强,但收敛速度减慢。下面以转子电阻为例,利用Matlab对p值进行辅助设计,根据式(32)~式(37),图5所示为不同p值下,电机转子电阻增大50%时,观测器的极点轨迹对比。由计算结果可知,p取值越大,因转子电阻偏差而引起的极点轨迹偏移越严重。综合考虑观测器收敛速度和对扰动的抑制能力,并参考文献[15]中的结论,选取p=1.25。
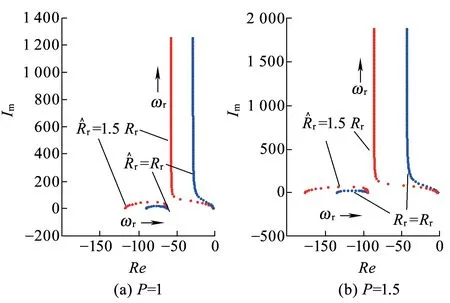
图5 转子电阻与p值设计的关系
初步选定p值后,对电机其他参数进行性能校验。图6为p取值1.25时,定子电阻、激磁电感和铁耗电阻偏移50%时的观测器极点轨迹图。可见,上述p值条件下,激磁电感、铁耗电阻和定子电阻的参数偏移对观测器两个极点影响较小,验证了上述极点配置方法对参数扰动的抑制效果。
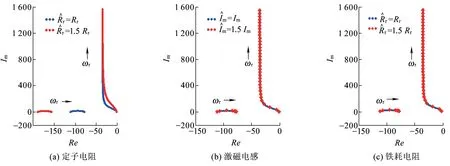
图6 p值取1.25时,对定子电阻、激磁电感和铁耗电阻参数扰动的抑制效果
3 自适应辨识
由上文分析和文献[10]的论述可知,损耗模型法的优化效果依赖于电机参数,且定子电阻和铁耗等效电阻影响较大,因此本章对这两个参数的自适应辨识进行研究,解决优化算法的参数敏感性问题。
3.1 系统误差方程
将上文设计的状态观测器系数矩阵写成方阵
(38)
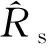
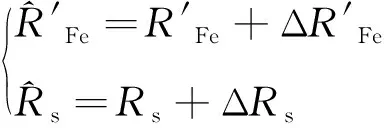
(39)
根据式(39),可将式(38)写成
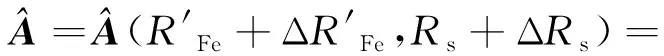
(40)
其中
(41)
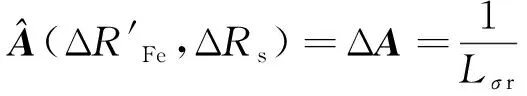
(42)
将电机模型写成状态方程标准形式
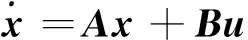
(43)
闭环模型(25)可改写为
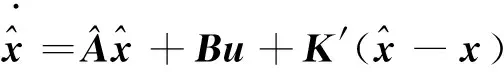
(44)
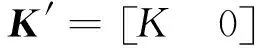
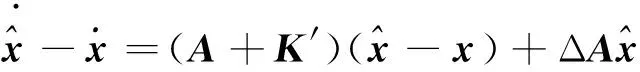
(45)
定义观测器误差
(46)
由此得到误差状态方程为
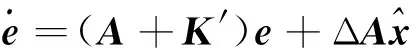
(47)
3.2 辨识自适应律设计
本节对自适应律进行设计,通过设计满足稳定性定律的自适应率,调节定子电阻的辨识值和铁耗电阻倒数的辨识值,令误差状态收敛于0附近,可认为观测器参数与电机参数相当,从而完成辨识。
构造李雅普诺夫函数
(48)
显然V≥0,对V求导,化简可得
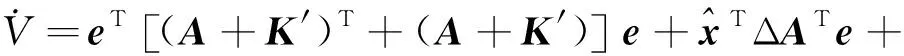
(49)
结合式(42)、式(47),对式(49)进行化简,可得
(50)
其中
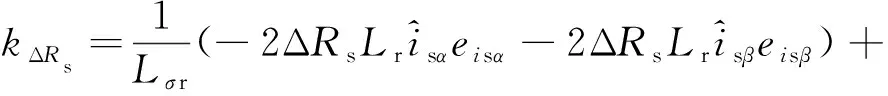
(51)
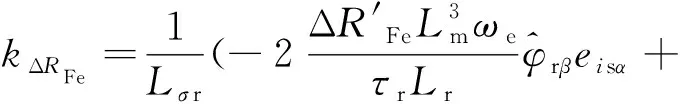
(52)
式(52)中的磁链误差项较难计算,由于定、转子漏感较小,忽略漏感则可消去磁链误差项,式(52)可简化为
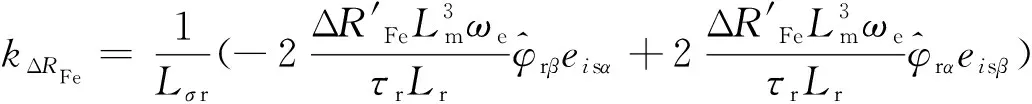
(53)
要满足李雅普诺夫稳定性定律,需保证式(50)负定,由于观测器极点被配置为电机极点的p倍,保证了式(50)的第一项负定[16],因此只需满足式(51)和式(53)等于0即可,求解得
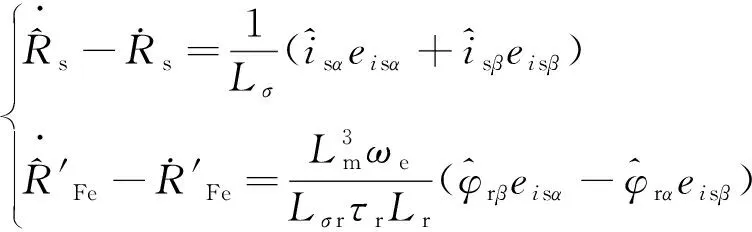
(54)
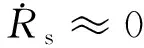
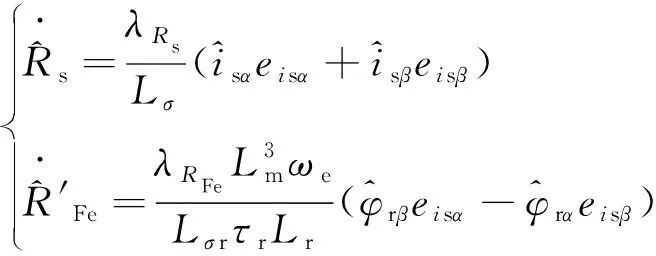
(55)
式(55)即为理论推导得到的定子电阻和铁耗等效电阻倒数的自适应辨识方法,控制框图如图7所示。
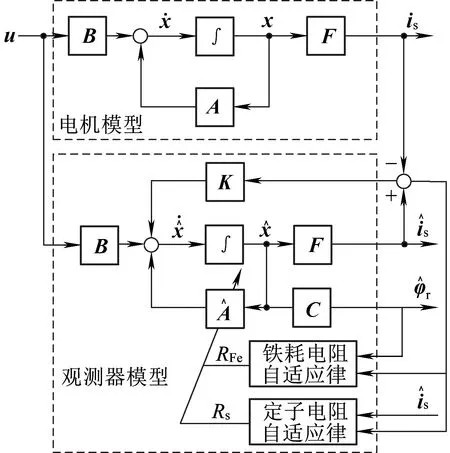
图7 带自适应辨识功能的闭环状态观测器
3.3 辨识算法的参数敏感性
式(55)所示的自适应辨识算法如图8所示,其包含其他电机参数,在实际应用中需加以改进。
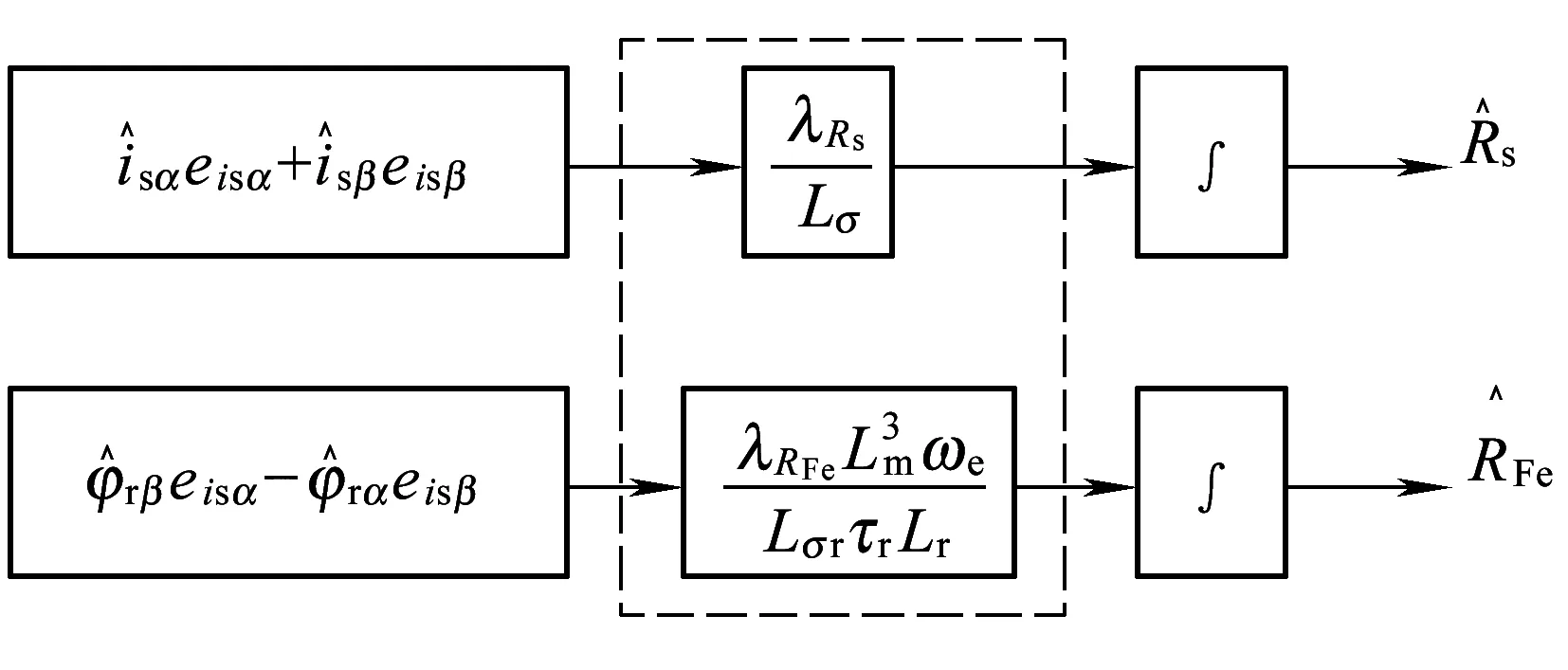
图8 初步理论推导的辨识算法
由式(55)可知,之所以对参数敏感,其本质是因为部分电机参数作为积分器的系数,电机运行过程中的参数偏移会被辨识算法累积放大。实际应用中可用积分系数取代电机参数,将式(55)改造成一个比例积分控制器,如图9和式(56)所示。
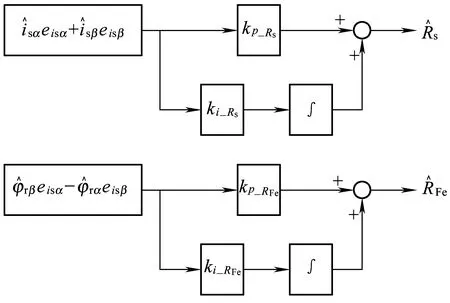
图9 优化的辨识算法
(56)
4 仿真与实验
4.1 仿真分析
为了验证上文所述算法,以Matlab/Simulink为工具搭建仿真模型。并联铁耗电阻额定值约为200 Ω,其他参数见表1。
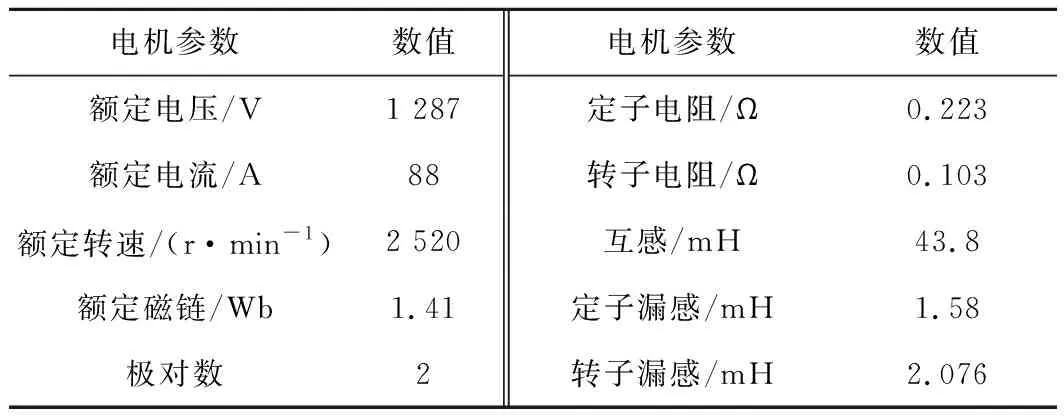
表1 电机参数
由于Matlab库中的电机模型未考虑铁耗,本节仿真用的电机模型采用S-function[17]编程实现。其状态方程如式(16)所示,转矩和运动方程为
(57)
(58)
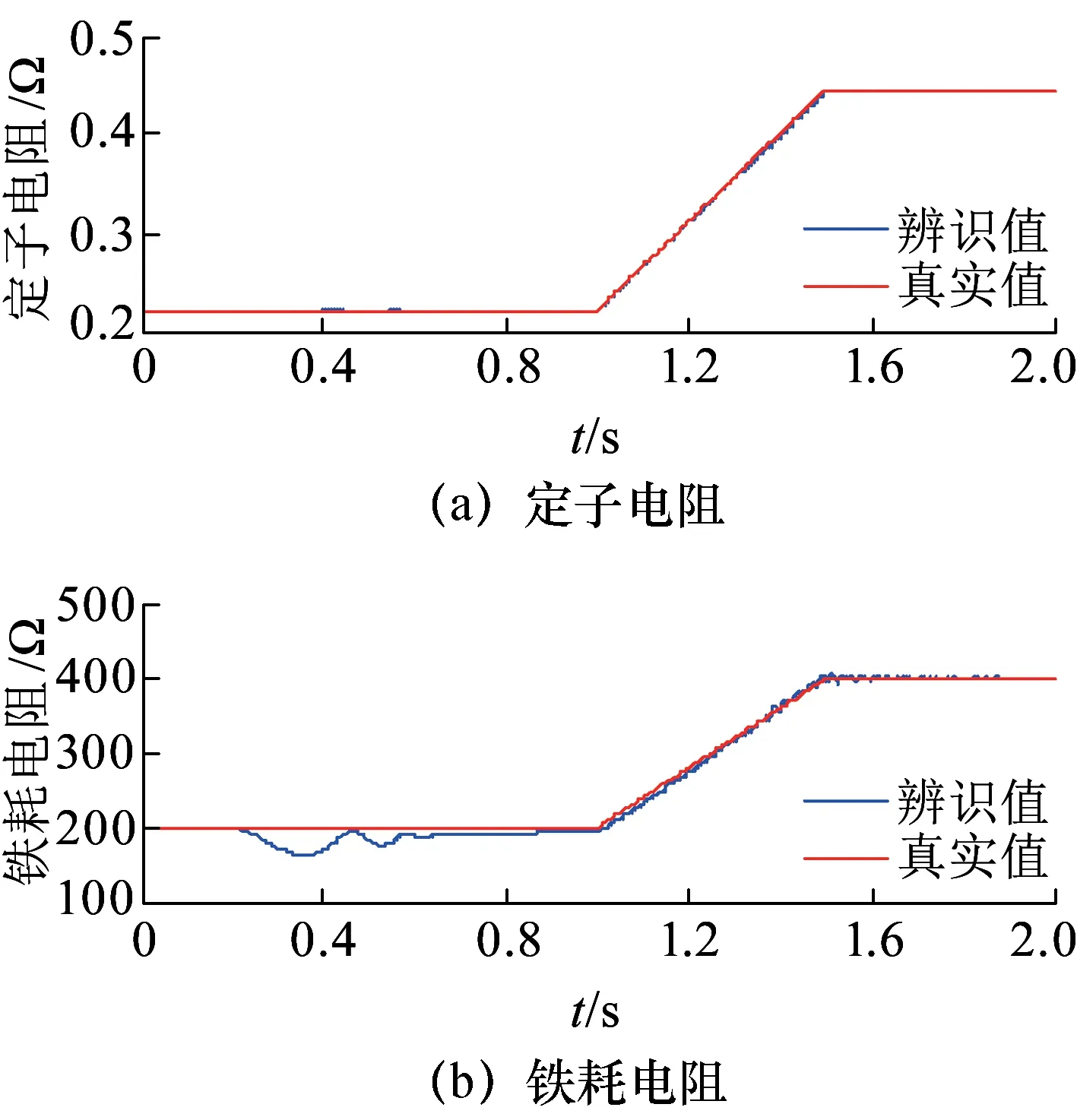
图10 斜坡响应仿真波形
为了充分验证算法性能,分别设计了斜坡响应仿真和阶跃响应仿真,以验证算法的追踪性能和参数阶跃跳变时的动态性能。斜坡响应如图10所示,可以看到,电机模型中的定子电阻和铁耗电阻从额定值斜坡增大至2倍额定值的过程中,辨识算法能较好的实现跟踪。阶跃响应如图11所示,从仿真结果可见,电机参数发生阶跃变化时,辨识值仍能较快响应,具有较好的动态性能。
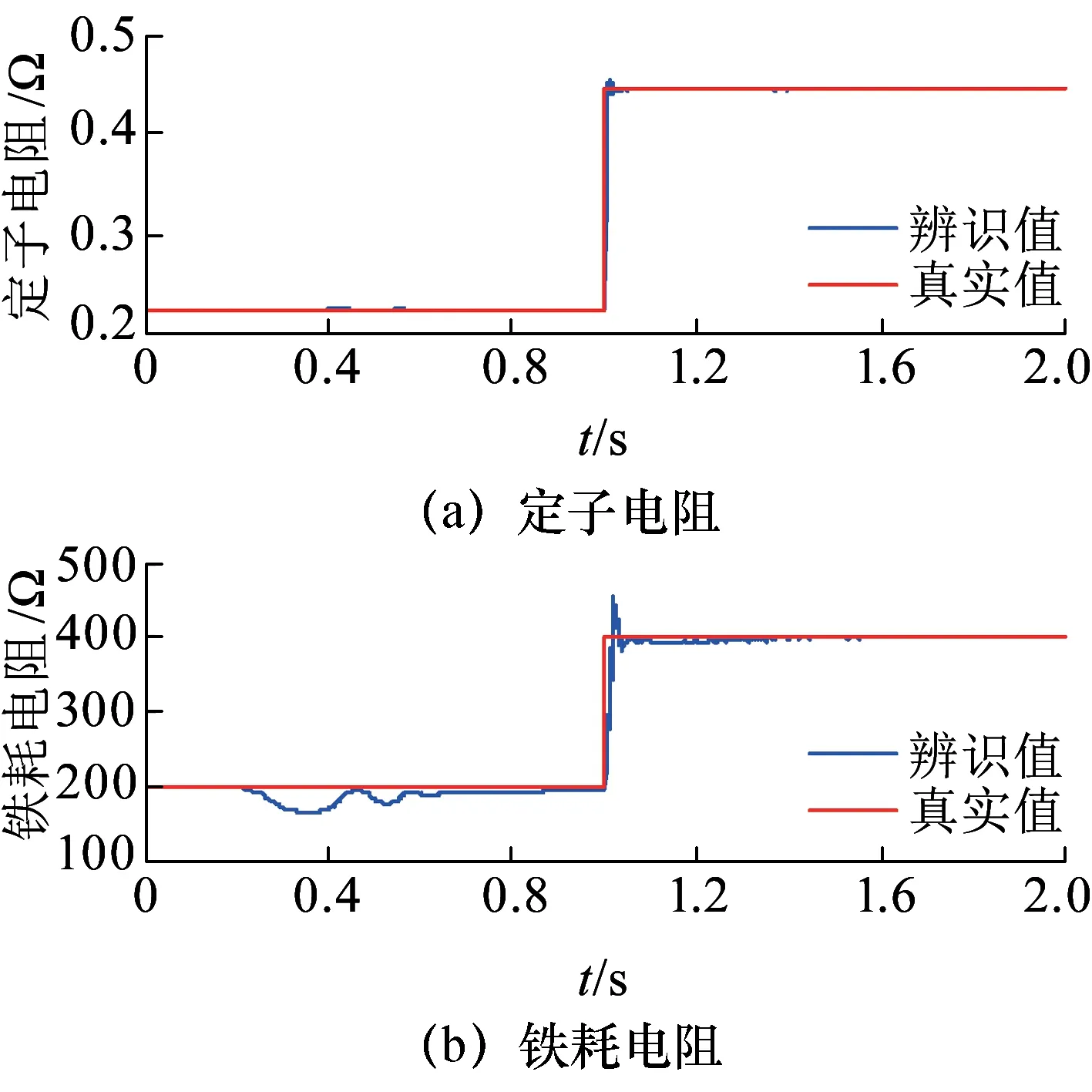
图11 阶跃响应仿真波形
下面对上文所述辨识算法的参数敏感性进行分析。由图8可知,理论推导的辨识算法中,定子电阻辨识几乎不受电机参数影响,而铁耗电阻的辨识与转子电阻关系较大。因此主要分析铁耗电阻辨识算法对转子电阻的参数敏感性。图12给出了转子电阻增大50%时理论方法与改进算法的辨识对比。图12(a)所示辨识波动较大,且收敛较慢,而改进算法经过了短暂的调节过程很快跟踪了实际值,表现出了较好的辨识性能。
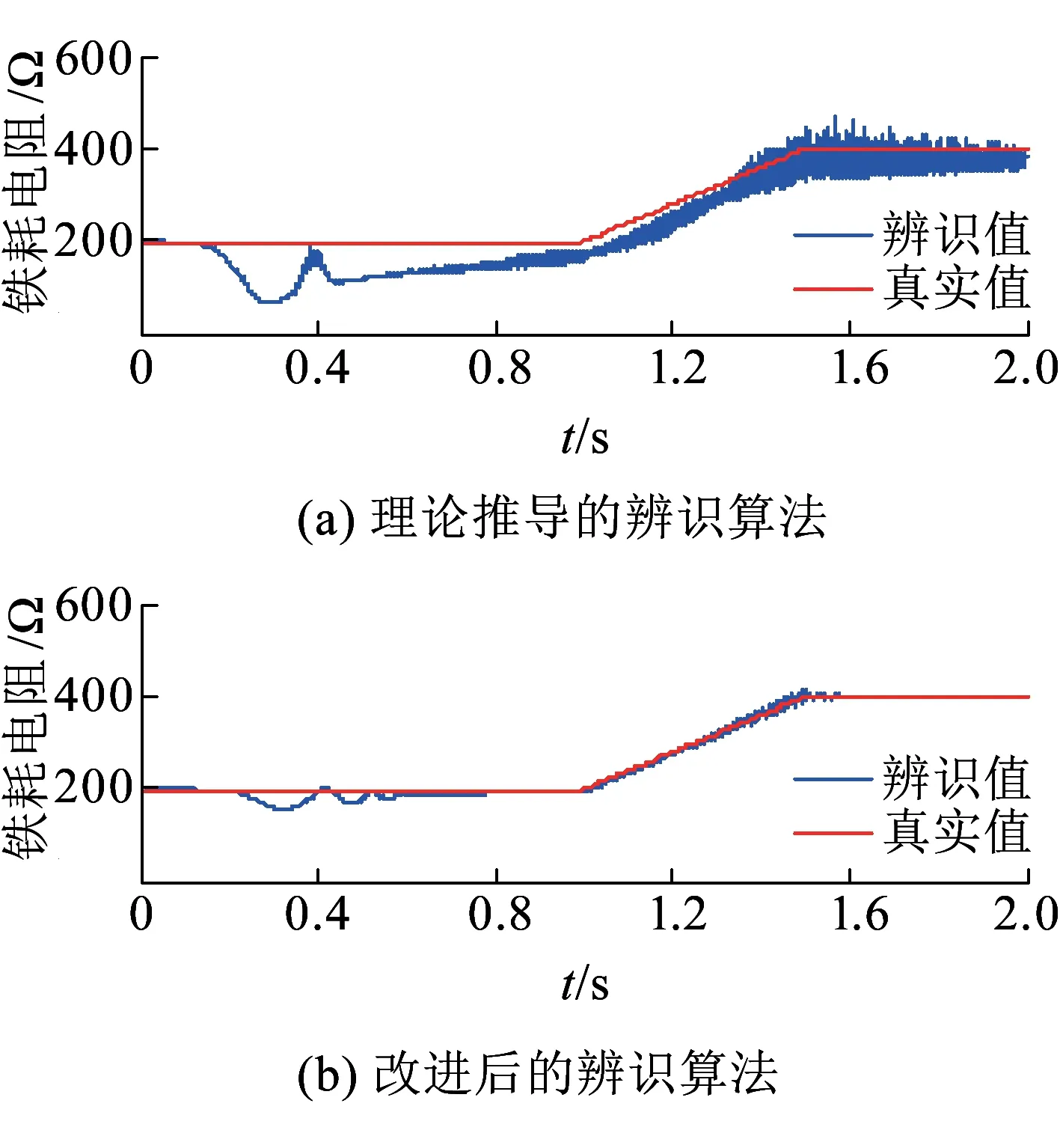
图12 辨识算法参数敏感性仿真对比
图13所示为加入本文辨识算法后的损耗模型法仿真结果,2 s之前未采用损耗模型法,2 s时投入优化算法,三条曲线分别为经过低通滤波处理的电机效率、损耗及输出功率对比。投入优化算法后,电机效率从82%上升至92%,电机损耗从10 kW降至4 kW左右,优化效果较明显。
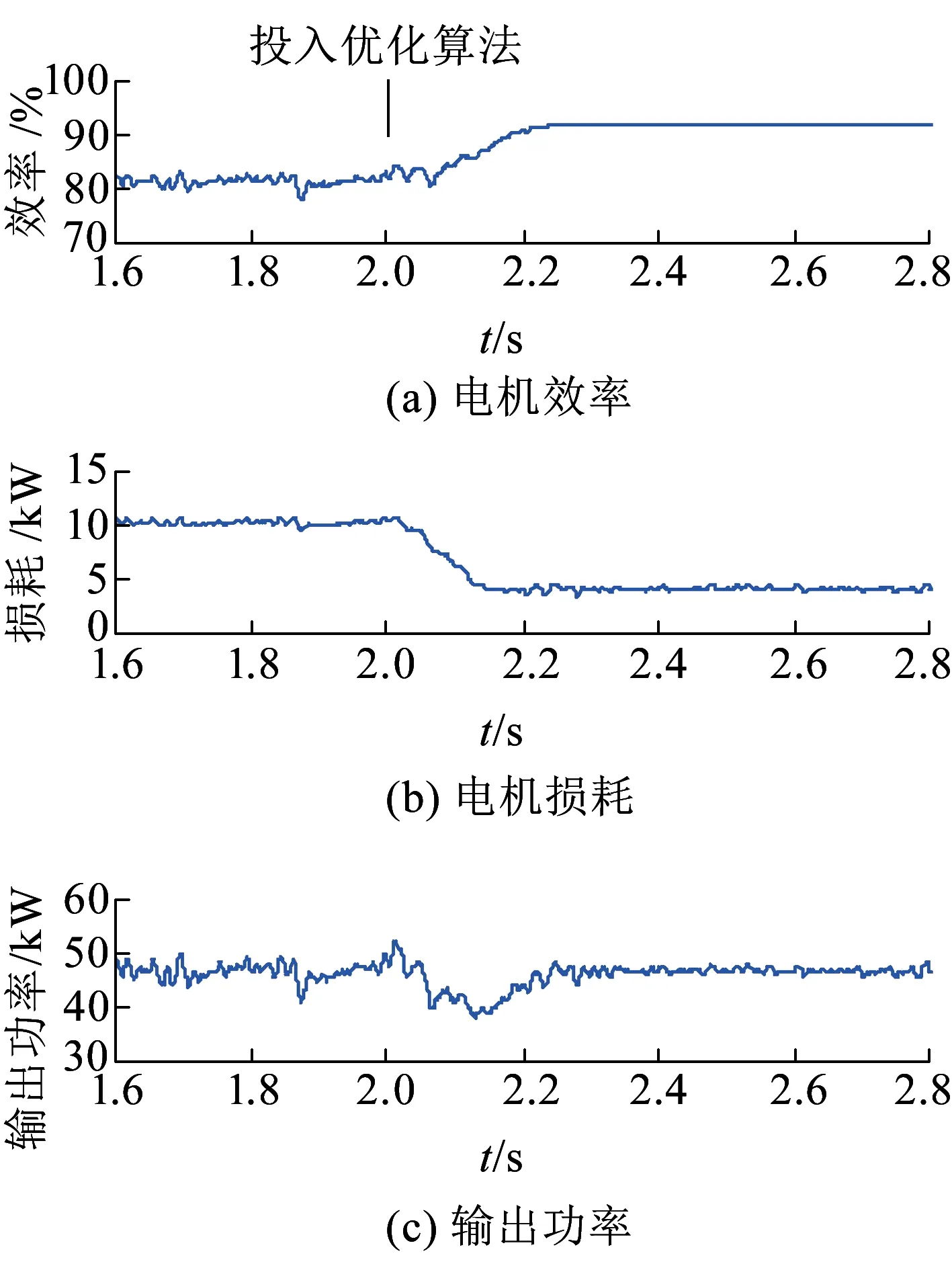
图13 效率优化算法投入前后效率、损耗及输出功率对比
4.2 实验验证
为了进一步验证本文所提方法,基于实际异步电机和两电平IGBT逆变器构成的实验平台,采用DSP+FPGA编程和虚拟仪器监控,实验用直流电压1 650 V,电机参数与仿真相同,得到图14~图16所示结果。
定子电阻和铁耗电阻辨识效果如图14和图15所示。其中定子电阻辨识初始值人为设置为0.5倍额定值,启用辨识算法后,经过短暂的暂态过程,定子电阻辨识值逼近额定值并保持稳定。铁耗电阻的辨识目前没有较权威的验证方法,本文采取实验记录数据并绘制铁耗电阻辨识值与定子频率的关系曲线,与铁耗电阻理论值进行对比的方法。铁耗电阻理论值见式(59),且目前主流理论对n的取值分别为0.7和1.6[10]。从图15所示曲线可知,辨识结果与n=0.7的理论值较接近,可近似认为实验所用电机的铁耗等效电阻符合n=0.7的变化规律。
(59)
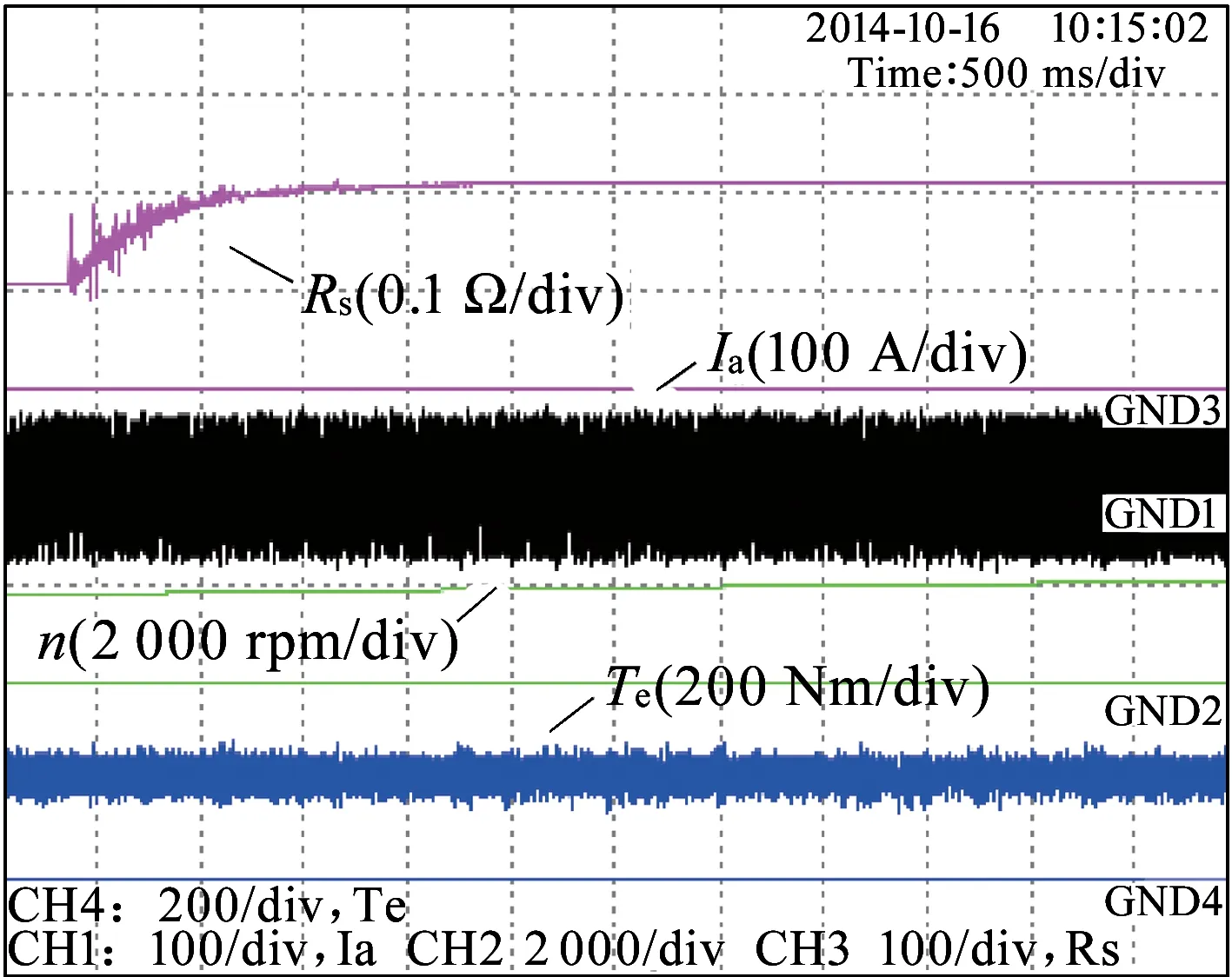
图14 定子电阻辨识
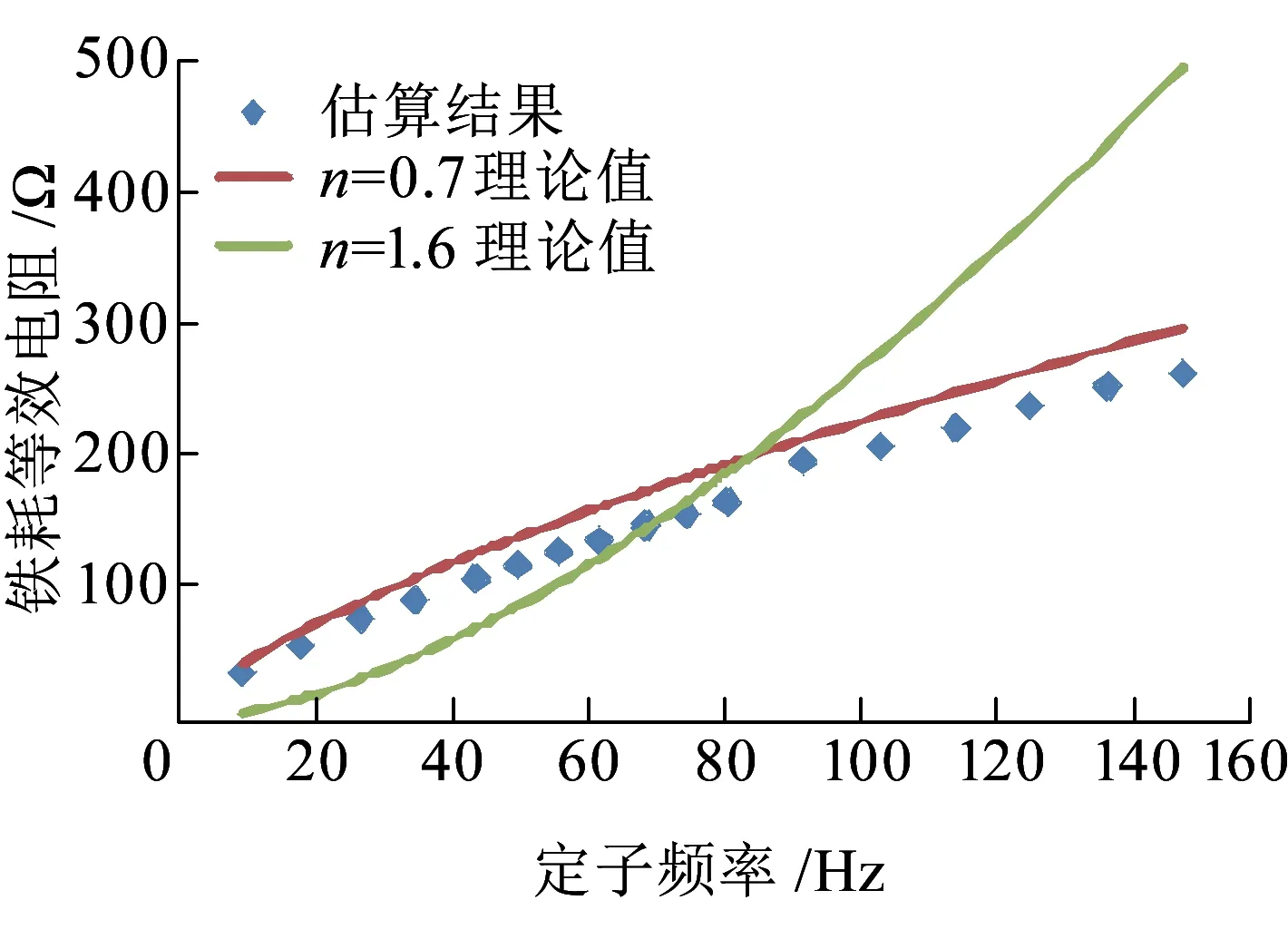
图15 铁耗等效电阻辨识
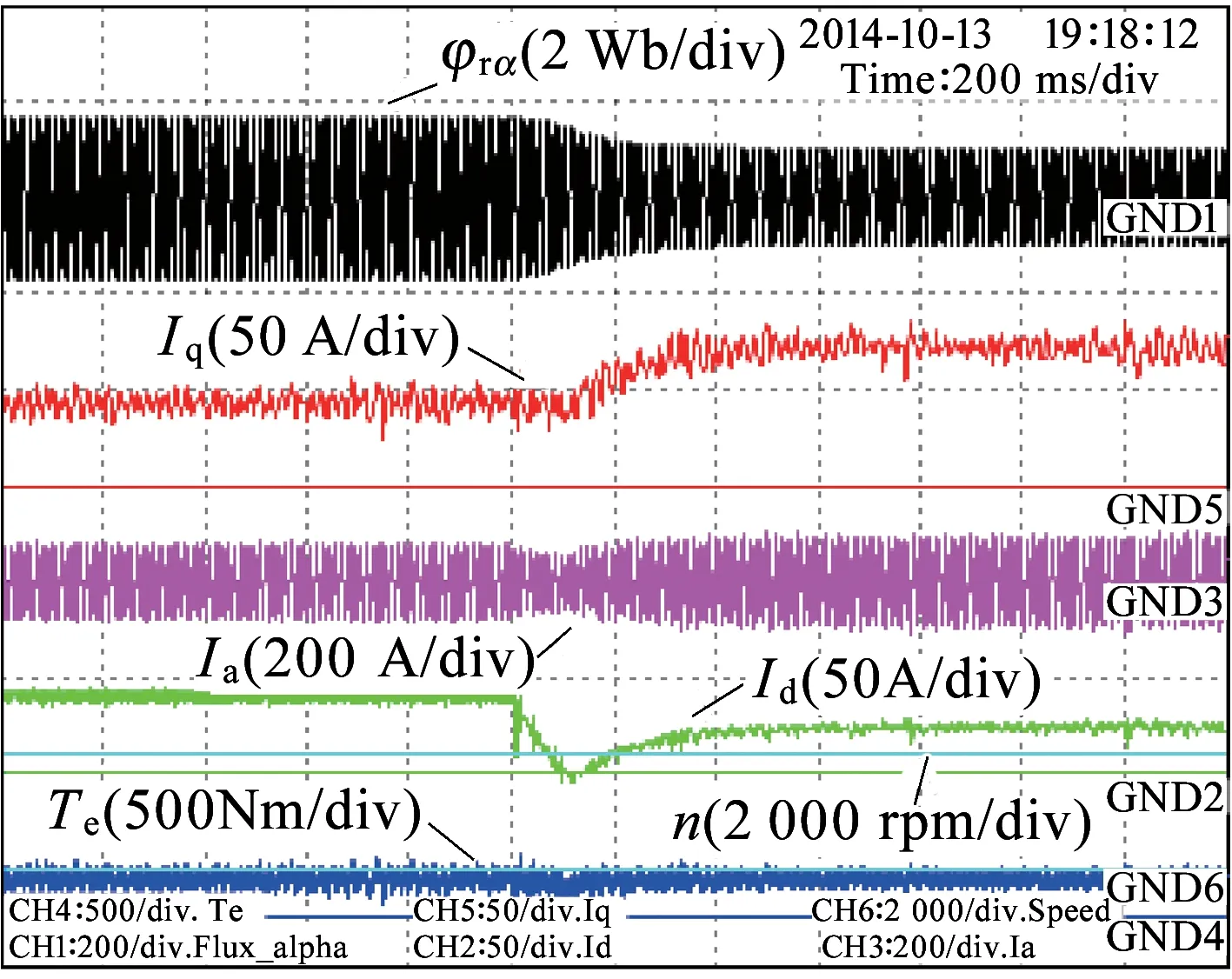
图16 效率优化控制实验结果,负载转矩200 Nm
对加入辨识算法的效率优化控制进行验证,采取的方法是电机先以传统控制加速至额定频率,待转速稳定后投入本文控制策略,对优化前后的效率和相关电量进行对比,结果如图16所示。图16所示工况负载转矩为200 Nm,波形依次为转子磁链观测值α轴分量、转矩电流反馈值、电机相电流、励磁电流反馈值、电机转速以及电磁转矩。投入优化算法后,电机磁链指令减小,实验结果中的转子磁链观测值和励磁电流反馈值相应减小,转矩电流分量则相应增大。通过功率分析仪和扭矩仪分别测量电机输入有功和轴端输出功率,得到优化前后效率分别为85.3%和90.5%,且在优化过程中转矩和转速较稳定,表现出了较好的控制性能。
5 结束语
基于损耗模型的电机效率优化算法因其物理意义明确、寻优速度快等优点而受到广泛关注,然而该方法对电机参数较为敏感,要提高优化效果,需实时准确获取相关电机参数。本文对电机关键参数进行了自适应辨识研究设计了考虑铁耗的电机状态观测器,并通过极点配置提高了观测器收敛速度和参数鲁棒性;基于稳定性分析设计了参数辨识自适应律,实现了定子电阻和铁耗等效电阻的在线辨识;通过仿真和实验对本文理论的可行性和有效性进行了验证。

