含腐蚀及椭圆度缺陷管道的动态屈曲传播研究

李牧之，余建星，余杨，段晶辉，韩梦雪，李杨，于佳晖



含腐蚀及椭圆度缺陷管道的动态屈曲传播研究

李牧之1, 2，余建星1, 2，余杨1, 2，段晶辉1, 2，韩梦雪1, 2，李杨1, 2，于佳晖1, 2

(1.天津大学 水利工程仿真与安全国家重点试验室，天津，300072；2. 高新船舶与深海开发装备协同创新中心，上海，200240)

通过建立有限元模型对海底管道的真实工况进行数值模拟，计算准静态条件下的管道压溃压力以及屈曲传播压力，并与管道全尺寸试验结果以及DNV-OS-F101规范中的计算结果进行对比，验证模型的准确性；在有限元模型中利用数据传递的方法将准静态条件下管道局部压溃的受力状态传递到动态模型中，并对管道在动态条件下的变形特点进行探究；研究管道腐蚀深度、初始椭圆度以及加载的传播压力对屈曲剖面长度、屈曲传播速度和反向椭圆度等管道动态屈曲传播特征值的影响。研究结果表明：在加载压力较小时，管道屈曲剖面长度随压力增大而减小；管道屈曲传播速度随着压力和初始缺陷的增大而加快；管道反向椭圆度的出现会阻碍屈曲沿管道轴线的传播，管道反向椭圆度随压力增大而增大。

海底管道；动态传播；初始椭圆度缺陷；片腐蚀缺陷

海底管道作为海上油气田的“生命线”，始终处在深海高压的工作环境中，一旦局部发生腐蚀或落物撞击等意外事故而导致管道性能下降，将发生局部压溃，这种压溃变形将沿着管道长度方向发生屈曲传播现象[1]屈曲传播会从发生局部压溃的位置开始，沿着管道轴线一直向下传播，直到外部环境压力低于屈曲传播压力或遇到局部加强结构为止。引起海底管道局部失效的常见因素包括腐蚀、地震、海水冲刷、船舶起抛锚作业以及管道在铺设过程中的损伤等，其中因腐蚀而导致海底管道破坏的事故占总事故的比例大于1/3[2]，是造成巨大经济损失的首要因素。自从1970年美国Battelle Columbus实验室[3]发现屈曲传播现象以来，国内外研究者对此进行了大量的理论和试验研究。PALMER等[4]对管道的屈曲传播现象进行了深入的理论研究，他们采用二维圆环模型进行计算，认为在屈曲传播之后管道被破坏为“哑铃”形状，并由此推导出屈曲传播压力的计算公式。CROLL[5]在其工作基础上把发生局部屈曲的管道分为压溃段、过渡段和未屈曲段3个部分，探究在何种情况下未屈曲段管道会沿着管道轴线向下转变为过渡段和压溃段管道。KYIAKIDES等[6−8]对准静态和动态下的缩尺比管道屈曲情况进行了研究。ALBERMANI等[9−10]通过高压舱试验计算出管道的屈曲传播压力并与圆环压溃试验结果进行了对比。RAMASAMY等[11]运用有限元分析软件ABAQUS对不同缺陷形式的管道进行了非线性计算，得出大口径管道在缺陷端部的压溃压力和屈曲传播压力。贾旭等[12]基于弹性力学理论，根据单层保温管道的结构特点、横截面上作用力的层间传递特性和变形协调条件，建立了静水压力作用下海底单层保温管道的屈曲分析方法。余建星等[13−15]运用深海结构压力舱，进行了全尺寸屈曲传播的准静态试验，根据得到的试验结果对管道在深海环境下的性能表现进行评估，并对局部压溃压力和屈曲传播压力进行了计算。刘源等[16]针对深海管道的压溃问题，采用二维模型模拟了管道和止屈器之间的接触情况，并分析了管道在外压和接触共同作用下的管道压溃形式。陈飞宇等[17]研究了在弯曲、轴力和外压的联合作用下的管道屈曲压溃问题，认为多种载荷对管道压溃压力的影响并不是单一载荷的线性叠加。GONG等[18]运用二维理论模型，研究了复杂载荷作用下海底管道的失稳机理。由此可见，目前的研究重点为局部屈曲发生的条件以及屈曲传播压力。人们对管道的局部屈曲及屈曲的传播在准静态条件下的研究很多，而对动态条件下的屈曲传播速度等动态特征值的研究较少。海底管道的动态条件即管道在实际深海作业中所处的恒定高压环境。在现有的准静态条件下的试验中，在加载舱内以水为介质对管道外部进行压力加载，管道外部压力逐渐上升直到管道缺陷段发生压溃，在管道被压扁后，发生大位移导致其外部压力骤降，屈曲无法向下传播。随着水的不断注入，管道的外部压力逐步趋于平稳，屈曲开始沿管道轴向传播，此时稳定下来的压力就是准静态条件下的屈曲传播压力。而海底管道的动态条件则要求维持外部压力环境稳定，即动态条件下的屈曲传播试验需要在整个试验过程中保持外部压力恒定。在实际工程中，铺设在海床上的海底管道外部所受的压力基本上是恒定的，一旦管道发生局部屈曲或压溃，屈曲就会沿着管线轴线方向高速传播[19]，此状态下的速度是准静态试验中测得的管道屈曲传播速度的数倍，带来的危害以及经济损失要比准静态条件下严重得多。基于海底管道真实工况的动态特性，对含有缺陷管道的动态屈曲模型进行研究，更有实际意义。本文作者利用有限元软件ABAQUS对管道的压溃过程进行建模分析，利用弧长法(Riks)模拟存在初始缺陷管道的准静态压溃形式，并与全尺寸管道试验结果以及DNV-OS-F101规范中的计算结果进行对比，以验证模型的准确性；在此基础上，采用数据传递的方法把管道静态模型的计算结果传递到动态模型中，从而模拟海底管道的动态条件，并对管道的屈曲剖面长度、屈曲传播速度以及反向椭圆度等动态特征值进行研究。由于不同管道在服役过程中所遭受的破坏形式以及所处的外部压力环境各不相同，故改变动态加载压力、初始椭圆度缺陷以及管道片腐蚀缺陷程度，探究管道在海底发生屈曲破坏时，其动态特征值的变化情况。

1 模型准确性验证

1.1 全尺寸管道模型试验

天津大学建造的全尺寸深海压力舱如图1所示。该装置总长11.5 m，直径为1.6 m，可模拟4.3 km水深的深海压力环境进行1:1等比例管道试验。本次试验所采用的管道模型基本参数如表1所示。在试验过程中，通过加压泵逐步对全尺寸管道施加水压，当水压达到管道所能承受的极限值后，管道将发生压溃，进而发生屈曲传播。根据整个试验过程中水压的加载曲线，可以得到管道在初始缺陷处的压溃压力以及管道整体的屈曲传播压力。

采用ABAQUS软件对试验过程进行数值模拟。其中，有限元模型中的几何参数和材料参数与试验管道的参数一致，通过Riks算法来追踪管道压溃及屈曲传播的全过程。有限元模拟与试验压力加载曲线对比如图2所示。图2中，c为管道的压溃压力，pr为屈曲传播压力。管道变形试验结果和数值模拟结果对比如图3所示。

图1 全尺寸深海压力舱

表1 管道参数

1—模拟压力加载曲线；2—试验压力加载曲线

1.2 DNV规范

DNV-OS-F101规范[20]中关于海底管道压溃压力c与屈曲传播压力pr的计算公式如下：

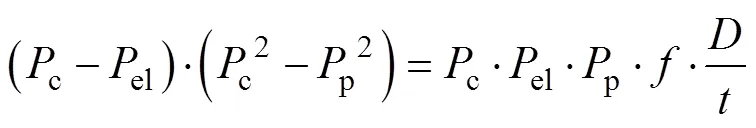
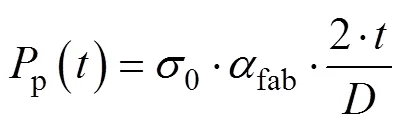
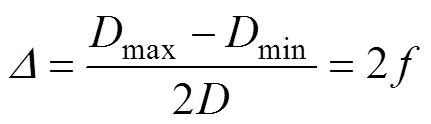
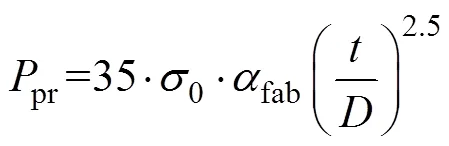
式中：为管道外径；为壁厚；el，p和为辅助计算参数；为弹性模量；为泊松比；max为管道缺陷处椭圆截面的最大直径；min为椭圆最小直径；0为管道材料的屈服强度；为椭圆度；fab为管道的制造系数，取0.93。

将c和pr有限元模拟结果分别与管道试验结果和DNV-OS-F101规范(下面简称为DNV规范)计算结果进行对比，如表2所示。由表2可以看出：采用弧长法进行准静态建模得到的结果与DNV规范计算结果以及试验结果吻合。运用3种方法所得到的压溃压力及屈曲传播压力一致，证明有限元模型可以较好地模拟管道的压溃过程。

(a) 管道变形试验结果；(b) 管道变形数值模拟结果

表2 不同方法下Pc和Ppr对比

2 动态屈曲传播过程

动态屈曲传播过程的实现是在准静态条件下使存在缺陷的管道达到压溃后，通过数据传递的方法将已经出现局部屈曲的管道模型传递到能够维持管道外压稳定的动态分析步中，进而得到动态条件下的管道屈曲传播情况。数值模拟中采用的管道模型外径为 44.4 mm，壁厚为1.659 mm，在管道外表面设置一定的腐蚀削薄作为管道初始缺陷，管道腐蚀示意图如图5所示。

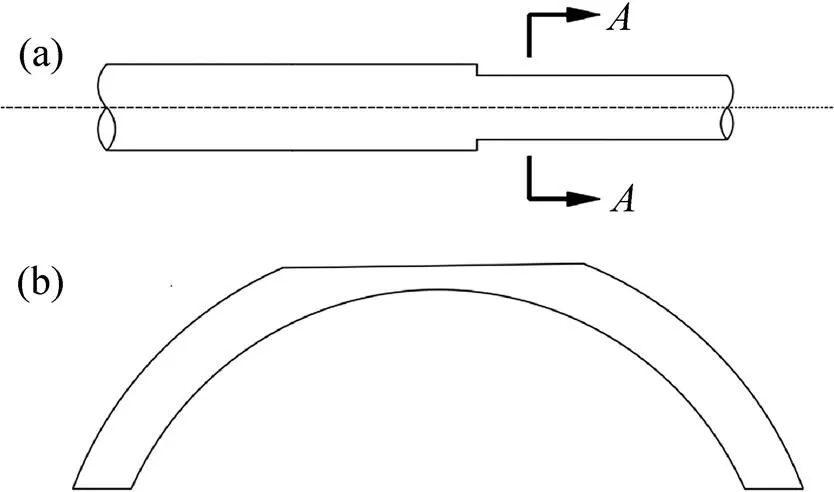
(a) A−A截面；(b) A−A截面的部分放大图

在ABAQUS软件的CAE模块中建立管道的准静态模型，分别定义管道的几何形状、材料属性、接触、约束和载荷等，并完成网格划分，采用弧长法计算得到局部屈曲的管道准静态模型。

在准静态的计算结果中，选取管道在缺陷处已经发生轻微压溃的某一分析步的状态，通过数据传递的方法传递到动态模型中，作为动态模型的初始状态，同时选择动态显式分析方法对管道动态屈曲传播参数进行计算。但这种方法仅导入准静态分析完成后的材料属性和网格变形情况，需另定义加载条件、边界条件以及接触条件等。

采用数据传递的方法相当于在准静态条件下模拟管道在缺陷处的破坏，并将管道的局部压溃变形形式传递到下一步，同时重新设定分析模式，保证管道外部压力的恒定，从而满足动态计算的条件。不同动态时间下管道屈曲传播如图6所示。从图6中可以看出：在管道端部产生局部压溃后，随着时间的变化，屈曲在恒定外压下沿着管道轴线快速向下传播。

同时，需要对椭圆度、腐蚀深度以及恒定外部压力等管道的屈曲特征参数进行敏感性分析。若反复在ABAQUS/CAE中修改这些参数，则需要对每一个模型都进行繁琐的建模过程，耗时耗力。所以，为了方便对管道模型的修改以进行敏感性分析，本文作者通过直接修改建模过程中的操作语句(Python)来简化分析过程。

动态加载时间/ms：(a) 初始状态；(b) 1；(c) 2；(d) 3

3 管道动态屈曲传播特征值

3.1 管道屈曲剖面长度

通过修改Python语句的方法，建立管片腐蚀深度分别为0.05，0.1，0.15和0.25 mm，初始椭圆度分别为0，1%，2%和3%的管道准静态模型。通过数据传递，对管道的动态模型施加不同的压力诱发屈曲传播，管道屈曲剖面长度随加载压力的变化如图7所示。

由图7可见：1) 随着初始缺陷即初始椭圆度和腐蚀深度增大，管道屈曲剖面长度也随之增大，拟合公式中可采用完备的二次多项式表示；2) 同一管道的屈曲剖面长度与动态模型中施加的外部压力无明显关系。

在上述结果中，诱发屈曲传播的压力与屈曲剖面长度之间无明显规律，这是因为在管道动态模型的数值模拟中对管道外表面施加的压力过大。为此，本文作者采用更加密集的压力加载梯度，对不同压力下的管道屈曲剖面长度的变化进行进一步分析研究。

以腐蚀深度为0.1 mm并含有1%椭圆度的管道为研究对象，先采用弧长法对准静态模型进行计算，得到此管道的屈曲传播压力pr为2.76 MPa。因此，只需在动态模型中施加大于2.76 MPa的压力，屈曲即可沿着管道轴线方向传播。通过多组计算后得到在腐蚀深度为0.1 mm并含有1%椭圆度的管道在不同动态加载压力下的屈曲剖面量纲一长度如图8所示(其中，为屈曲剖面长度，为加载的动态压力)。由图8可以看出：当1.0＜/pr＜2.0时，屈曲剖面长度随着动态压力的增大而减小；当/pr＞2.0时，加载的动态压力对屈曲剖面长度并无明显影响。将数值计算结果拟合后得到如下表达式：

椭圆度/%：(a) 0；(b) 1；(c) 2；(d) 3

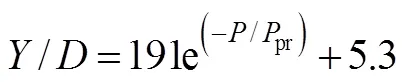
3.2 屈曲传播速度

对腐蚀深度为0.05~0.25 mm的管道施加不同的压力诱发屈曲传播，得到屈曲传播速度随加载压力的变化，如图9所示。为了能够更直观地得出各因素对屈曲传播速度变化的影响，对屈曲传播速度进行拟合：

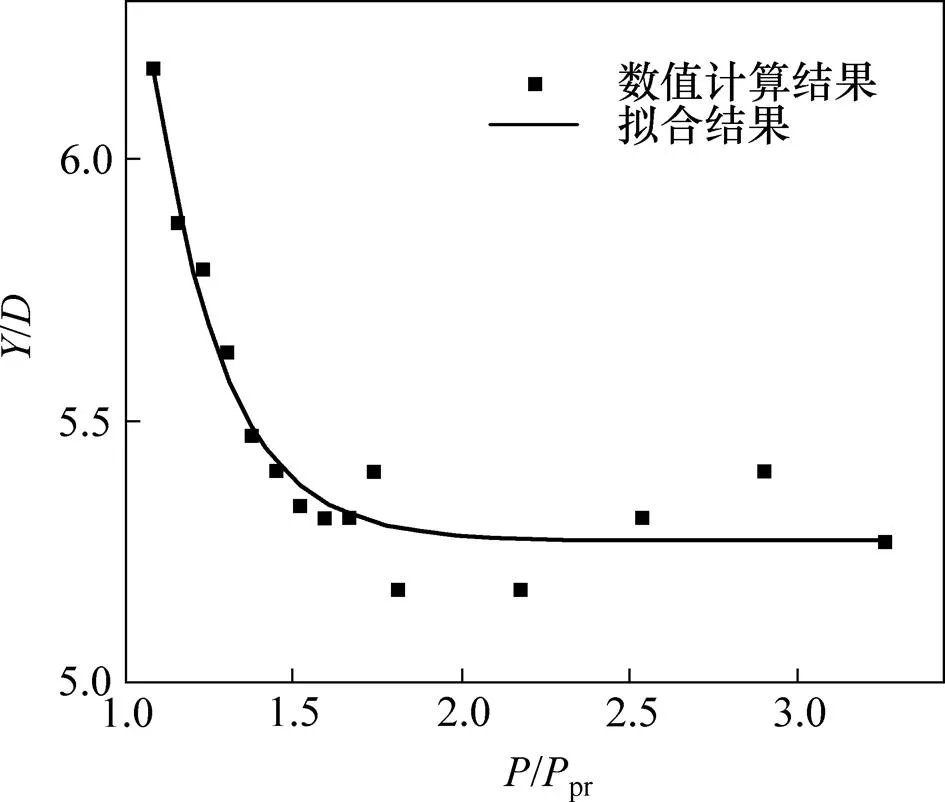
图8 　管道在不同加载压力下的屈曲剖面量纲一长度

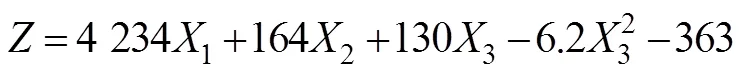
式中：为屈曲传播速度；1为椭圆度；2为腐蚀深度；3为压力。

式(8)中校正后的相关系数为0.966 64，拟合结果较好。

由图9可见：1)屈曲传播速度与管道的初始缺陷，即初始椭圆度以及腐蚀深度呈正比，可采用线性关系描述其对应关系；2)施加的动态加载压力与屈曲传播速度呈正相关，可采用二次多项式表示。

在屈曲动态传播的过程中，外力做功等于外压与管道变形体积的乘积，此能量使管道从弹性进入塑性阶段，还有部分能量消散在流体中。在能量平衡的状态下，外压越大，外力做功就越大，管道进入到塑性阶段所需的时间就越短，屈曲传播速度也就越大。

3.3 反向椭圆度

建立腐蚀深度为0.05 mm、无初始椭圆度的管道模型，选择屈曲传播到管道中段速度稳定的阶段进行反向椭圆度分析。

采用弧长法所得计算结果中，此管道模型的屈曲传播压力pr为6 MPa，在动态模型中对其施加6 MPa的恒定压力，选择管道中段进行椭圆度分析，管道椭圆度随量纲一距离的变化如图10所示。其中，轴正值表示管道存在正向椭圆度，负值则表示管道存在与初始椭圆度相悖的反向椭圆度。

从图10可以看出：1) 前半段正向椭圆度较大部分为屈曲剖面的一部分，管道在此时已经出现较小的屈曲状态；2) 在选取的管道区域的后半部分，出现反向椭圆度以阻碍屈曲的平行传播；3) 反向椭圆度的绝对值先增大再减小，最终会趋于0；4) 即使对管道施加等同于屈曲传播压力的动态加载压力，只要屈曲能够沿着管道轴线向下传播，就一定存在反向椭圆度 以阻碍屈曲向下传播的趋势，换言之，反向椭圆度与正向椭圆度一样，在屈曲的传播过程中都是普遍存 在的。

椭圆度/%：(a) 0；(b) 1；(c) 2；(d) 3

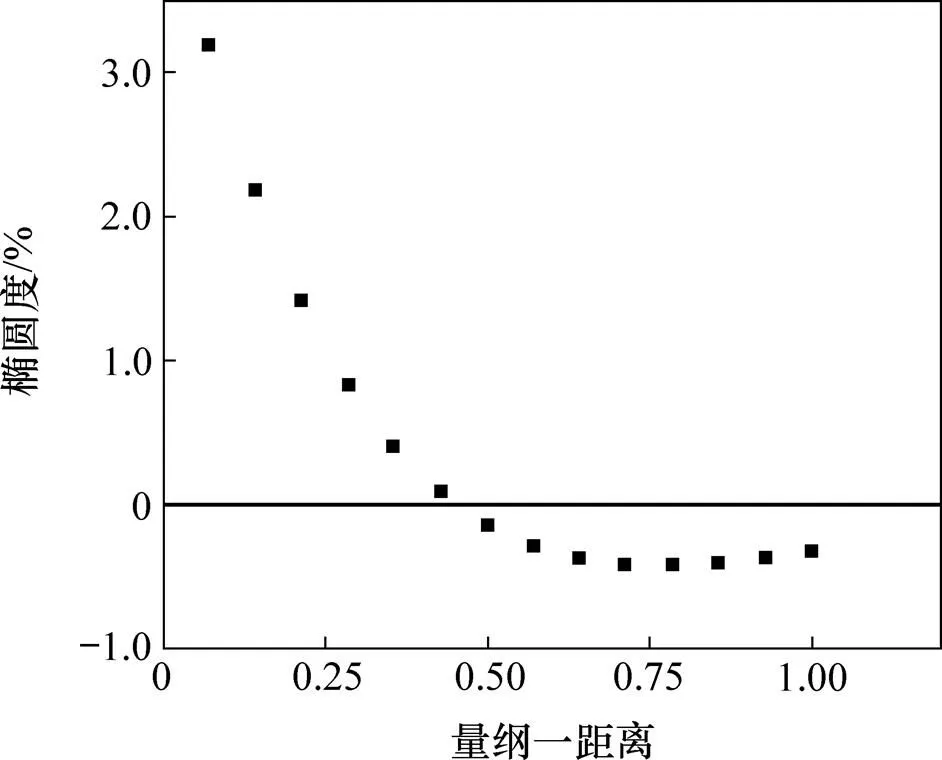
图10　压力为6 MPa时管道椭圆度随量纲一距离的变化

为了探究不同动态压力下管道的椭圆度变化情况，在相同管道模型中分别施加不同的压力诱发屈曲传播。同一路径上管道椭圆度变化如图11所示。从图11可以看出：随着压力增大，管道上出现的反向椭圆度也随之增大，但当压力较小时，同一路径上的椭圆度变化趋势基本相同，最大反向椭圆度虽然有增大趋势，但变化幅度不大；而当压力较大时，最大反向椭圆度变化幅度较大。在此基础上，可以将反向椭圆度与摩擦相类比，摩擦会阻碍物体的相对运动趋势，而反向椭圆度会阻碍屈曲沿着管道轴线向下平行传播的趋势。由此可见，在外部压力较小时，屈曲传播速度也较小，会出现较小的反向椭圆度阻碍屈曲的平行传播；而在外部压力较大时，屈曲传播速度加快，管道本身会阻碍平行传播，因而反向椭圆度也会增大。

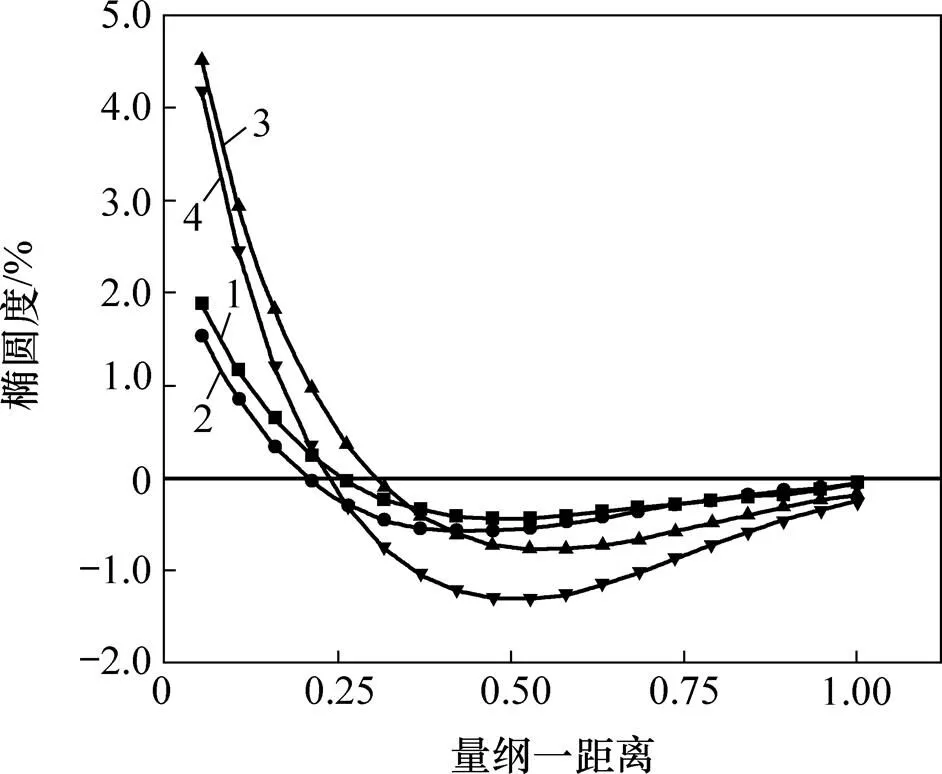
加载压力/MPa：1—7；2—9；3—10；4—11

3.4 正交传播

在反向椭圆度的敏感性分析中发现，如果对一段很长的、存在局部压溃的管道施加较大的动态加载压力时，屈曲会先沿着管道轴线向下平行传播一定的距离，随后，传播方向调转90°，并以该方向向下传播一段距离后，再恢复到原来的传播方向，这就是管道的正交屈曲传播。也可以说，由于管道在某一压力下出现了最大的反向椭圆度，进而引发了正交传播现象。管道正交传播示意图如图12所示。

图12　管道正交传播示意图

但是，在数值计算中发现，如果管道模型存在较大的正向初始椭圆度或一定的腐蚀深度，即使压力增大到管道的压溃压力，也只会加快屈曲传播的速度，并不会出现正交传播的形式。同时，正交传播是屈曲传播过程中反向椭圆度的最大化表现形式。由此可见，管道存在的初始椭圆度和腐蚀深度会对反向椭圆度产生一定的影响。

4 结论

1) 本文提出研究管道屈曲传播动态特征值的数值模型。通过弧长法对管道前期准静态条件下的压溃模态进行模拟，使模型能够在不同的动态压力下完成屈曲传播，同时利用全尺寸试验结果和规范DNV-OS-F101中的计算结果验证了模型的准确性；借助数据传递的方法将准静态模型中已经在缺陷处出现明显压溃的管道应力状态和变形情况传递到动态模型中，完成恒定压力下海洋环境的模拟，并对动态屈曲传播的重要特征参数进行分析。

2) 对于屈曲剖面长度来说，在动态屈曲传播模型中，当动态加载压力较小时，屈曲剖面长度随着压力的增大而减小，当加载的压力较大时，压力对屈曲剖面长度并无明显影响；随着管道初始缺陷的增大，屈曲剖面长度也有一定程度增大。对于屈曲传播速度来说，传播速度随着动态加载压力和初始缺陷的增大而加快，用多项式即可较好地拟合速度和各参数的关系。

3) 反向椭圆度与正向椭圆度一样，在屈曲的传播过程中都是普遍存在的；在外部压力较小时，屈曲传播速度也较小，会出现较小的反向椭圆度阻碍屈曲的平行传播；在外部压力较大时，屈曲传播速度加快，管道本身会阻碍平行传播的趋势，因而，反向椭圆度也会增大，并且管道存在的初始椭圆度和腐蚀深度会对反向椭圆度产生一定的影响。

[1] 翟宇轩, 余建星, 孙震洲, 等.海底管道整体式止屈器的止屈性能研究[J]. 天津理工大学学报, 2014, 30(5): 46−51.

ZHAI Yuxuan, YU Jianxing, SUN Zhenzhou, et al. The arresting performance of integral buckle arrestors for offshore pipelines[J]. Journal of Tianjin University of Technology, 2014, 30(5): 46−51.

[2] 曹永升, 王沙, 赵晨, 等. 海底集输管道的破坏与防护[J]. 化学工程与装备, 2013(7): 98−99.

CAO Yongsheng, WANG Sha, ZHAO Chen, et al. Destruction and protection for the offshore gathering pipeline[J]. Chemical Engineering & Equipment, 2013(7): 98−99.

[3] MESLOH R E, SORENSON J E, ATTERBURY T J. Buckling and offshore pipelines[J]. Gas, 1973(7): 40−43.

[4] PALMER A C, MARTIN J H. Buckle propagation in submarine pipelines [J]. Nature, 1975, 254: 46−48.

[5] CROLL J G A. Analysis of buckle propagation in marine pipelines[J]. Journal of Constructional Steel Research, 1985, 5(2): 103−122.

[6] KYRIAKIDES S, CHANG Y C. On the effect of axial tension on the propagation pressure of long cylindrical shells[J]. International Journal of Mechanical Sciences, 1992, 34(1): 3−15.

[7] KYRIAKIDES S, NETTO T A. On the dynamics of propagating buckles in pipelines[J]. International Journal of Solids & Structures, 2000, 37(46/47): 6843−6867.

[8] CORONA E, KYRIAKIDES S. On the collapse of inelastic tubes under combined bending and pressure[J]. International Journal of Solids & Structures, 2015, 24(5): 505−535.

[9] ALBERMANI F, KHALILPASHA H, KARAMPOUR H. Propagation buckling in deep sub-sea pipelines[J]. Engineering Structures, 2011, 33(9): 2547−2553.

[10] KHALILPASHA H, ALBERMANI F. Hyperbaric chamber test of subsea pipelines[J]. Thin-Walled Structures, 2013, 71: 1−6.

[11] RAMASAMY R, TUAN YA T M Y S. Nonlinear finite element analysis of collapse and post-collapse behaviour in dented submarine pipelines[J]. Applied Ocean Research, 2014, 46: 116−123.

[12] 贾旭, 侯静, 田英辉. 静水压力作用下海底单层保温管道压溃屈曲分析[J]. 中国海上油气, 2006, 18(5): 341−343.

JIA Xu, HOU Jing, TIAN Yinghui. The buckling analysis on single layer insulation pipeline acting by external hydrostatic pressure[J]. China Offshore Oil and Gas, 2006, 18(5): 341−343.

[13] 余建星, 卞雪航, 余杨, 等. 深水海底管道全尺寸压溃试验及数值模拟[J]. 天津大学学报(自然科学与工程技术版), 2012, 45(2): 154−159.

YU Jianxing, BIAN Xuehang, YU Yang, et al. Full-scale collapse test and numerical simulation of deepwater pipeline [J]. Journal of Tianjin University(Science and Technology), 2012, 45(2): 154−159.

[14] 余建星, 李骁, 徐立新, 等. 深水海底管道凹陷机理[J]. 天津大学学报(自然科学与工程技术版), 2015, 48(11): 1009−1013.

YU Jianxing, LI Xiao, XU Lixin, et al. Denting mechanism of deepwater pipeline[J]. Journal of TianJin University(Science and Technology), 2015, 48(11): 1009−1013.

[15] YU Jianxing, SUN Zhenzhou, LIU Xiaoxie, et al. Ring–truss theory on offshore pipelines buckle propagation[J]. Thin-Walled Structures, 2014, 85: 313−323.

[16] 刘源, 苗春生, 余建星, 等. 海底管道屈曲传播中管壁与扣入式止屈器非线性接触问题研究[J]. 天津大学学报(自然科学与工程技术版), 2017, 50(3): 225−232.

LIU Yuan, MIAO Chunsheng, YU Jianxing, et al. Nonlinear contact between subsea pipeline and slip-on arrestor during the process of buckling propagation[J]. Journal of Tianjin University (Science and Technology), 2017, 50(3): 225−232.

[17] 陈飞宇, 余建星, 赵羿羽, 等. 复杂载荷条件下有缺陷海底管道非线性屈曲分析[J].中南大学学报(自然科学版), 2015,46(7): 2701−2706.

CHEN Feiyu, YU Jianxing, ZHAO Yiyu, et al. Nonlinear buckling of subsea pipes with imperfection under complex loads[J]. Journal of Central South University(Science and Technology), 2015, 46(7): 2701−2706.

[18] GONG Shunfeng, NI Xingyue, BAO Sheng, et al. Asymmetric collapse of offshore pipelines under external pressure[J]. Ships and Offshore Structures, 2013, 8(2): 176−188.

[19] KYRIAKIDES S, BABCOCK C D. On the dynamics and the arrest of the propagating buckle in offshore pipelines[C]// Proceedings of the Annual Offshore Technology Conference. Texas, USA. 1979: 1−12.

[20] DNV-OS-F101, Submarine pipeline systems[S].

Research on dynamic buckling propagation of pipeline with corrosion and ovality

LI Muzhi1, 2, YU Jianxing1, 2, YU Yang1, 2, DUAN Jinghui1, 2, HAN Mengxue1, 2, LI Yang1, 2, YU Jiahui1, 2

(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China; 2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China)

A finite element model was used to simulate the subsea pipelines in practical engineering. The results of collapse pressure and propagation pressure were compared with those of full-scale collapse test and the calculation results of DNV-OS-F101 specification, and the accuracy of the model was verified. A method called data transfer in the finite element simulation was used to transfer the quasi-static stress state of the collapsed pipeline to the dynamic model. In this way, the deformation characteristics of the pipeline under the dynamic condition was studied. Besides, the influences of corrosion depth, ovality and the external pressure on dynamic characteristic values of pipeline such as the length of buckle profile, the buckle velocity and the reverse ovality were researched. The results show that the length of buckle profile of pipeline decreases with the increase of loading pressure at low pressure. The buckle velocity of pipeline increases with the increase of pressure and the initial imperfection. The appearance of reverse ovality of pipeline will hinder the propagation of buckling along the pipeline axis, and the pipeline reverse ovality increases with the increase of pressure.

submarine pipeline; dynamic propagation; initial ovality defect; plate corrosion defect

P752

A

1672−7207(2019)05−1165−08

10.11817/j.issn.1672−7207.2019.05.020

2018−05−28；

2018−07−28

国家重大科技专项(2016ZX05028005-004)(Project(2016ZX05028005-004) supported by the National Science and Technology Major Program of China)

余杨，副教授，从事深海结构耦合动力分析、海洋平台运动控制研究，E-mail: yang.yu@tju.edu.cn

(编辑 伍锦花)