基于接触摩擦理论的岩壁吊车梁锚固设计

于 冲，杨社亚，张 睿，石广斌，郝春游，徐 明，冯 飞

(1.中国电建集团西北勘测设计研究院有限公司， 陕西 西安 710065；2.中国水利水电第十一工程局有限公司， 河南 郑州 450001； 3.西安建筑科技大学，陕西 西安 710055)

0 前 言

KSEP水电工程位于非洲赞比亚和津巴布韦界河——赞比西河的卡里巴峡谷段，北岸为赞比亚，南岸为津巴布韦，原装机容量750 MW。扩机工程装机两台，单机容量150 MW，总装机容量300 MW，为津巴布韦独立以来的最大工程。扩机工程由右岸地下引水发电系统、母线竖井、地面主变平台、地面电抗器平台、开敞式地面开关站等组成。2018年3月28日，津巴布韦总统埃默森·姆南加古瓦亲临扩机工程竣工仪式，为电站揭牌剪彩。KSEP水电站主厂房地质条件较好，地下洞室基本均为Ⅱ类围岩。

目前，岩壁吊车梁设计主要采用刚体极限平衡法、现场模型试验和现场量测、计算机数值仿真计算法等。传统的刚体极限平衡计算方法通常基于岩台地基反力基本按三角形分布、地基反力的合力通过岩台上某点、岩台下部锚杆与岩台面交点为力矩中心点等假定，并不能真实地反映岩壁吊车梁真实的受力机理和工作状态[1-6]。现场模型试验和现场量测费时、费力，且费用较大，国内仅在小湾水电站工程中进行了1 ∶1的模型试验[7]。以有限元为代表的数值计算方法及其软件的兴起和成熟，为岩壁吊车梁的设计提供了新的方法和手段。本文采用非线性有限单元法，精细模拟围岩、梁体、锚杆以及岩壁吊车梁与岩体的接触面，对岩壁吊车梁的受力特性进行了系统的计算分析。

1 岩壁吊车梁设计

岩壁吊车梁断面体型见图1，锚固设计见图2。梁体设计断面为2.0 m×2.9 m(宽×高)；锚固方案为：梁体上部二排锚杆为450 MPa级 T32钢筋，间距90 cm，入岩L=7.0 m，水平倾角20°和25°，岩台下部一排锚杆为450 MPa级 T32钢筋，间距90 cm，入岩L=4.8 m。

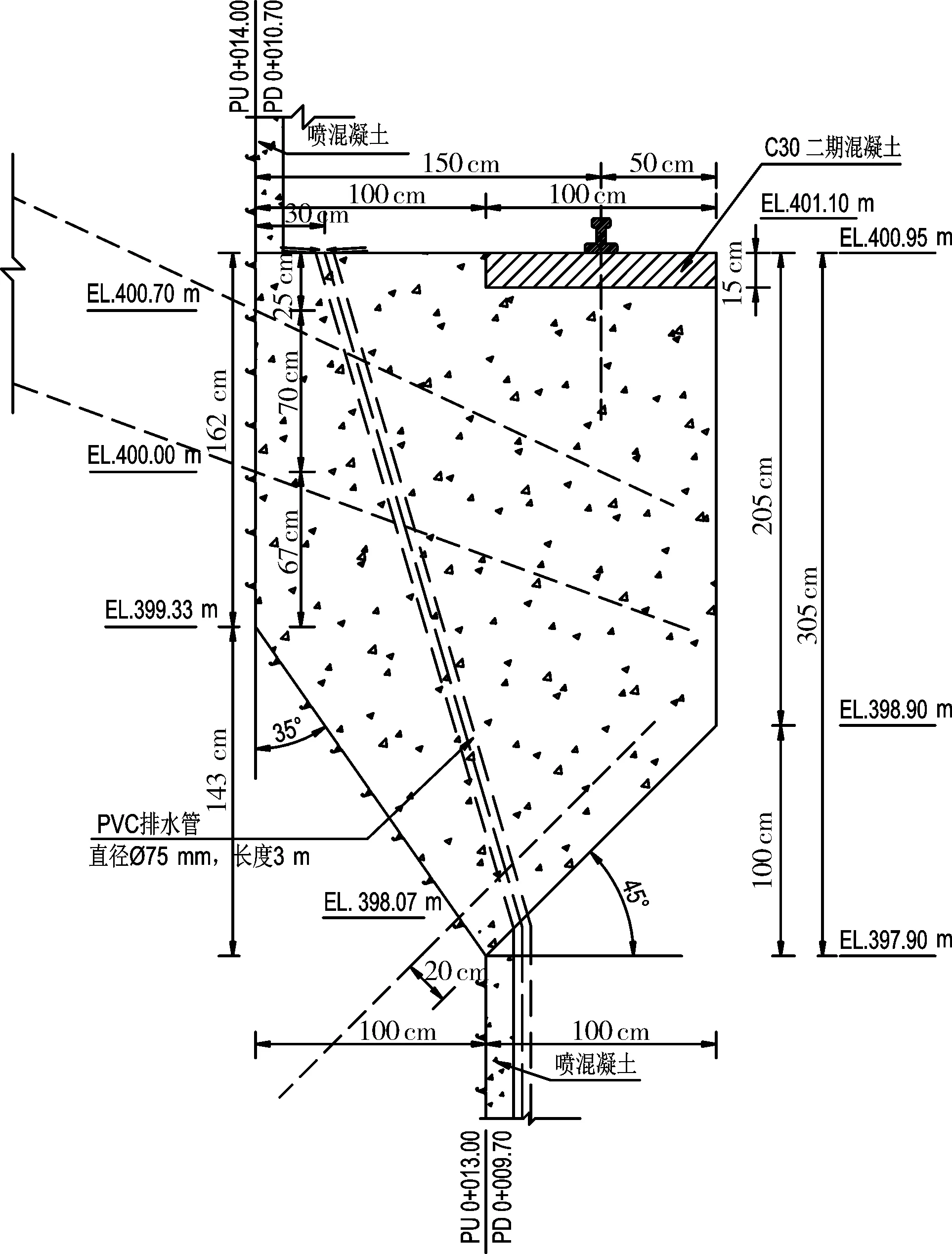
图1 岩壁吊车梁体型(比例尺 1 ∶20)

2 岩壁吊车梁有限元分析

2.1 物理力学参数

岩体及支护材料物理力学参数如表1、2所示。岩壁吊车梁与岩壁接触面分别按纯摩(黏聚力C=0，摩擦系数f=0.65)和混凝土/岩抗剪断(C′=1.1/2=0.55 MPa，f′=1.1/1.7=0.647)。

表 1 地下厂房区围岩物理力学参数

表2 支护材料物理力学参数

2.2 工况及载荷

(1)工况1(完建期工况)：只计岩壁吊车梁自重。

(2)工况2：运行期工况。

荷载组合：运行期荷载=吊车竖向轮压+吊车横向水平荷载+吊车梁自重荷载。

地下主厂房安装2台套250 t/50 t-21.7 m(分别为主钩、副钩及跨度)桥式起重机，桥机大车单个最大轮压为400 kN。由于吊车横向水平荷载有两个方向，本文选取最不利的工况进行计算，即横向水平荷载指向厂房内。

2.3 有限元计算模型

将岩壁吊车梁简化为平面应变问题进行分析，假定围岩和梁体为线弹性材料，研究在运行期吊车轮压、吊车横向水平荷载和吊车梁自重(含二期混凝土自重)、轨道及附件重等作用下岩壁吊车梁的变位、应力变化规律和锚杆的内力变化规律。

岩壁吊车梁二维有限元计算模型坐标系取水平方向为X轴，垂直向上为Y轴。岩体采用平面四边形8结点等参单元(PLANE82单元)，锚杆采用杆单元(LINK1单元)，岩壁吊车梁与围岩接触面采用接触单元(TARGE169、CONTA172)进行模拟。有限元模型边界条件：上部、下部和左侧边界施加固端约束，有限元模型见图3。

图3 岩壁吊车梁有限元计算模型

2.4 有限元计算结果

本节岩壁吊车梁锚固及结构有限元计算，综合考虑了梁体和围岩的相互接触和共同受力，更能真实地反映岩壁吊车梁的受力状态[8-11]。有限元计算得到的运行期上部二排锚杆、岩台下部锚杆的应力，不包括地下厂房施工期开挖、因围岩变位作用而赋存于锚杆中的应力，这部分应力可以通过结构系数γd和岩壁吊车梁监测资料综合考虑。

图4～7分别显示了完建期、运行期岩壁吊车梁锚杆应力分布，从锚杆应力图中可以看出上部第1排锚杆的拉力大于第2排锚杆的拉力。表3列出了不同荷载工况下上部两排锚杆的应力极值。采用纯摩参数，在运行期上部第1排锚杆的拉应力为158.666 MPa，第2排锚杆的拉应力为144.306 MPa；采用抗剪断参数，在运行期上部第1排锚杆的拉应力为92.835 MPa，第2排锚杆的拉应力为70.284 MPa。锚杆应力均小于锚杆360 MPa的强度设计值，且有一定的安全裕度。

图8～19分别显示了完建期、运行期岩壁吊车梁与岩台接触面上的应力分布情况。从图中可以分析出，运行期在岩壁吊车梁自重、竖向吊车轮压荷载、横向水平荷载等荷载的共同作用下，岩壁吊车梁将向厂房内侧变形，岩壁吊车梁与围岩的后缘接触面的正应力很小。采用纯摩参数，接触面的正应力和剪应力主要分布在岩台斜面；采用抗剪断参数接触面的正应力和剪应力主要集中在岩壁吊车梁下部锚杆与岩壁的交点至岩台下角点之间的范围内。

由有限元的计算结果得到：采用纯摩参数，岩壁吊车梁的抗滑稳定安全系数为1.0；采用抗剪断参数，岩壁吊车梁的抗滑稳定安全系数为1.1。岩壁吊车梁是稳定的。

图4 完建期岩壁吊车梁锚杆应力分布，纯摩参数(单位：kPa)

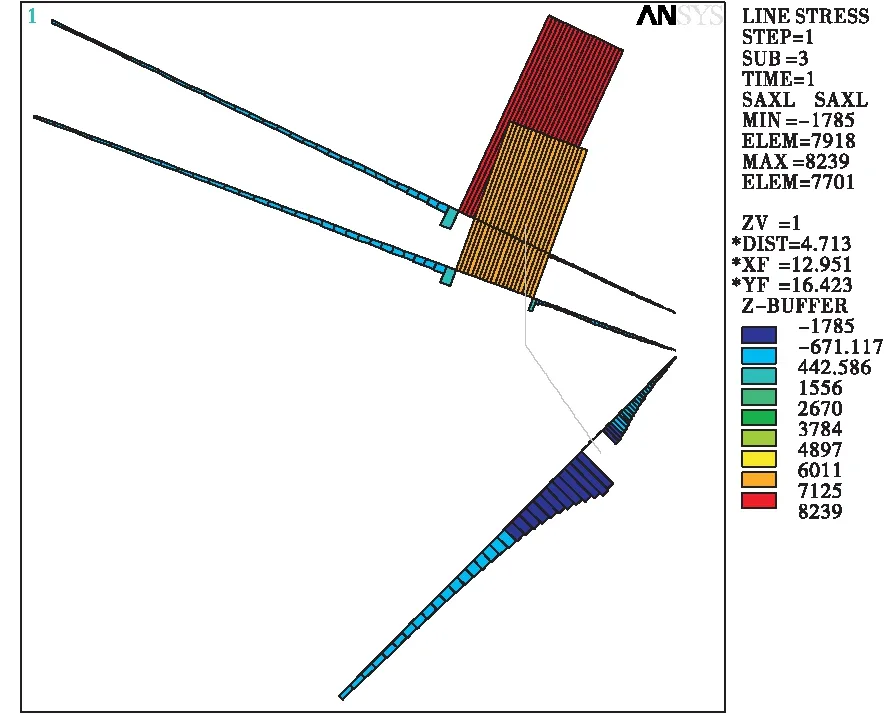
图5完建期岩壁吊车梁锚杆应力分布，抗剪断参数(单位：kPa)

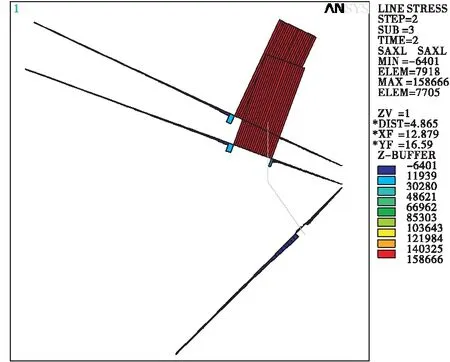
图6 运行期岩壁吊车梁锚杆应力分布，纯摩参数(单位：kPa)

图7运行期岩壁吊车梁锚杆应力分布，抗剪断参数(单位：kPa)

图8 完建期岩壁吊车梁与岩台接触面正应力，纯摩参数(单位：kPa)

图9完建期岩壁吊车梁与岩台接触面剪应力，纯摩参数(单位：kPa)

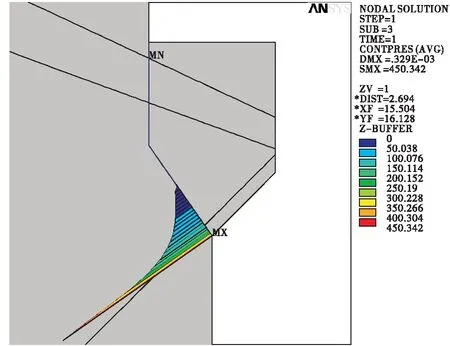
图10 完建期岩壁吊车梁与岩台接触面正应力，抗剪断参数(单位：kPa)

图11完建期岩壁吊车梁与岩台接触面剪应力，抗剪断参数(单位：kPa)

图12 运行期岩壁吊车梁与岩台接触面正应力，纯摩参数(单位：kPa)

图13运行期岩壁吊车梁与岩台接触面剪应力，纯摩参数(单位：kPa)

图14 运行期岩壁吊车梁与岩台接触面正应力，抗剪断参数(单位：kPa)

图15运行期岩壁吊车梁与岩台接触面剪应力，抗剪断参数(单位：kPa)

图16完建期岩壁吊车梁位移，纯摩参数(单位：m)

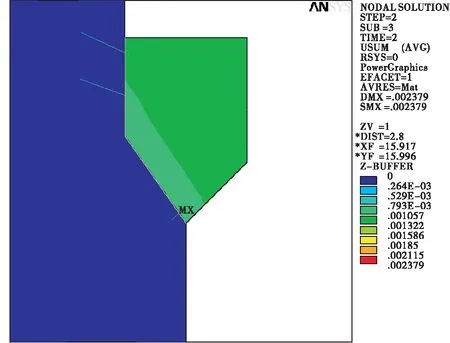
图17运行期岩壁吊车梁位移，纯摩参数(单位：m)

图18完建期岩壁吊车梁位移，抗剪断参数(单位：m)

图19运行期岩壁吊车梁位移，抗剪断参数(单位：m)

3 结 语

(1)基于接触摩擦理论，采用ANSYS软件对KSEP水电站岩壁吊车梁锚固结构进行了精细的有限元分析，计算得到的岩壁吊车梁上部两排受拉锚杆的抗拉承载力以及梁体的抗滑稳定均满足要求，且有一定的安全裕度。

(2)采用接触界面单元模拟滑动面，锚杆单元模拟岩壁梁上部二排锚杆、岩台下部锚杆，并且按照真实的桥机轮压施加荷载，较好地模拟了各种荷载工况下锚杆的受力状况及梁体与围岩的摩擦、滑动状态，可准确分析出不同工况下锚杆的内力、应力和滑动面的应力分布状态与安全性态，避免了传统“刚体极限平衡法”的各种假定，能更真实、全面反映岩壁吊车梁的工作性态及支护机理，对其他工程的岩壁吊车梁的稳定性分析、支护设计有较好的借鉴和指导作用。