改进二进制-实数编码混合蛙跳算法在水电机组短期发电调度中的应用

杨 哲，杨 侃，吴 云，夏 怡，齐伟擎，张天衍，仲晓林



改进二进制-实数编码混合蛙跳算法在水电机组短期发电调度中的应用

杨 哲１，杨 侃1，吴 云2，夏 怡1，齐伟擎1，张天衍1，仲晓林3

(1.河海大学水文水资源学院，南京 210098；2.山西水利职业技术学院，运城 044004；3.扬州市勘测设计研究院有限公司，扬州 225000)

本文将改进实数编码混合蛙跳算法(IR-SFLA)和二进制编码的(IB-SFLA)方法分别应用到水电站经济负荷分配(ELD)和机组组合(UC)问题，提出解决STHGS问题的IBR-SFLA方法．实数编码版本IR-SFLA利用混沌学遍历性、随机性特征生成初始种群，采用更新的局部搜索和位置更新策略实现青蛙更新换代，并在迭代后期通过自适应青蛙激活机制重新激发青蛙搜索能力；在二进制编码IB-SFLA中引入改良青蛙子种群分组方式，将青蛙种群分为领导蛙、追随蛙和变异蛙3类蛙群，各类蛙群分别基于正态云模型的精英进化策略、改进的局部搜索机制和混沌理论的蛙群变异操作进行更新迭代．运行结果显示IBR-SFLA相较对比算法，在低、中、高水头下最高缩减耗水量1.14×107、1.22×107、7.52×106m3，有效提升水能资源利用效率；在保证运算精度、稳定性的同时，平均运行时间最高缩减178、173和172s，进一步，改进策略性能分析显示，各改进策略可有效增强搜索性能，提升精度，且耗时增幅较小，在较小种群规模下便可获取较高质量的解，为解决大规模机组短期电力调度优化课题提供有效了新思路．

水电站机组短期发电调度(STHGS)；自适应青蛙激活机制；改良子种群分组方式；云模型精英进化策略；混沌蛙群变异

水电站机组短期发电调度(STHGS)问题的研究旨在满足水电站电网发电要求前提下，寻求最小的发电和机组启停水量消耗．通常STHGS可划分为两个子问题，一是水电站机组组合(unit commitment，UC)优化，决定运行时段内机组启停的时序组合，典型0～1规划问题；二是机组经济负荷分配(economic load distribution，ELD)，为连续空间约束问题，旨在对每台机组进行最优负荷分配．对机组组合和负荷分配优化可有助提升水能资源利用效率，增发电量，保证电网系统运行稳定．STHGS问题研究历经由传统数学到智能算法优化的过渡，传统数学方法以混合整数非线性规划、拉格朗日松弛法(LR)、二次规划(QP)和动态规划(DP)为主，以DP为例，此方法可以求出理论最优解，但面对较大规模机组组合易陷入“维数灾”，虽然传统方法取得了不同程度的优化效果，但在面对大规模机组发电优化问题时的运算效率和精度难以得到保证．随着人工智能的兴起，诸如萤火虫算法、万有引力算法(GSA)、烟花算法[1-3]等方法被应用到复杂水电站发电优化调度问题．与传统方法相比，智能算法不受约束条件的限制，凭借灵活的搜索策略和强大的收敛性能，可在较短时间内获取高质量的优化结果．与此同时，为进一步增强搜索和收敛性能，由两种或多种算法组合的混合方法被应用到STHGS问题优化．然而，上述方法在收敛性能和搜索精度等方面仍有提升空间．例如万有引力算法，虽然加入混沌理论来增强局部搜索能力，但整体效率、鲁棒性仍有待提升和改善；蚁群算法随着机组数目的增多，搜索效率显著下降，且参数设置可能会导致结果早熟．总体来说，对于STHGS问题，迫切寻求更高效的优化方法和工具．

混合蛙跳算法(SFLA)子种群内部信息交流和全局蛙群信息共享可有效引导算法向全局最优方向快速收敛，但仍存在“早熟”收敛弊端．为此，学者针对混合蛙跳算法进行改进，并应用于水资源、交通、电力系统等领域[4]．本文首先构建水电站机组短期发电模型，包含机组组合和负荷分配子模块；进而在传统SFLA基础上加以改进分别提出二进制编码IB-SFLA和实数编码IR-SFLA．前者用于解决UC子问题，改进策略为引入云模型和混沌理论，将蛙群分为3类子种群，每类子种群按各自搜索方式进行更新；后者被应用到经济负荷分配子问题，改进策略为基于改进Logistic映射的种群初始化和启发式青蛙激活机制，以及改良的蛙群局部搜索公式，从而提出二进制及实数编码混合蛙跳算法(improved binary and real-coded shuffled frog leaping algorithm，IBR-SFLA)．在三峡大规模水电站机组短期发电调度优化的应用，验证了算法在解决高维、非线性、离散发电调度问题中的高效性和适用性，为此类问题优化提供有效新方法．

1 短期水电站发电调度(STHGS)问题描述

1.1 经济负荷分配

经济负荷分配作为短期水电站发电调度子问题，旨在以最小水量消耗完成发电目标，目标函数为

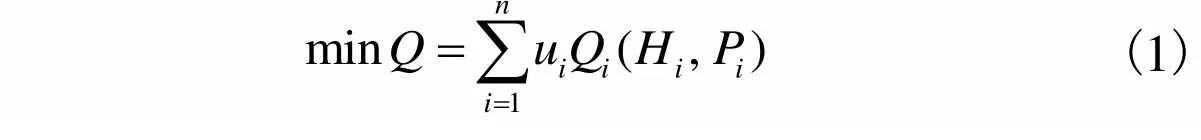
(1)

1.2 水电机组组合

机组组合问题是寻求机组开启和关闭的最优时序安排，减少发电和机组开启、关闭时水量的消耗．相应目标函数可描述为

(2)

1.3 约束条件

(1) 功率平衡约束为

(3)

(2) 旋转备用约束为

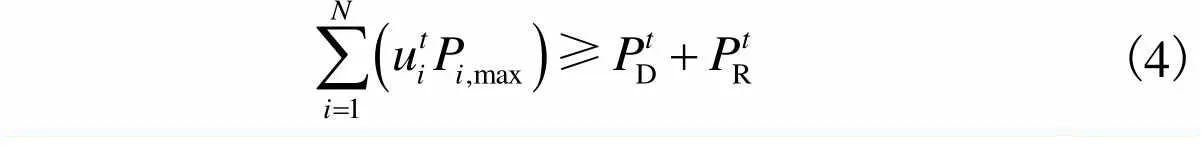
(4)

(3) 水电机组发电负荷约束为

(5)

(4) 禁止运行区约束为

(6)

(5) 最小启停时间约束为

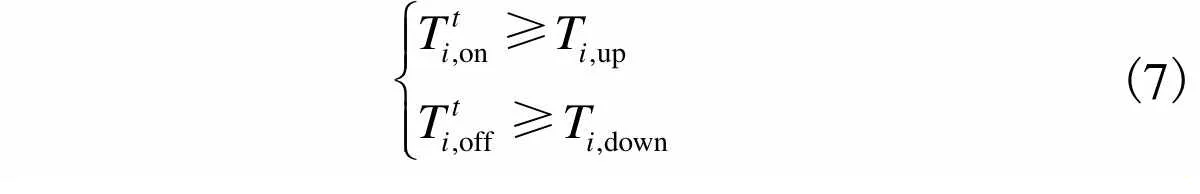
(7)

(6) 水电站调蓄和下泄流量约束为

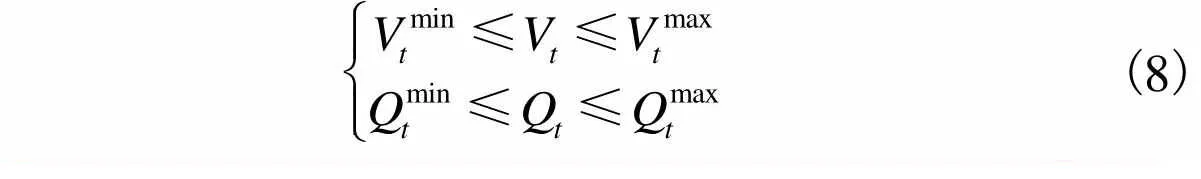
(8)

(7) 水量平衡约束为

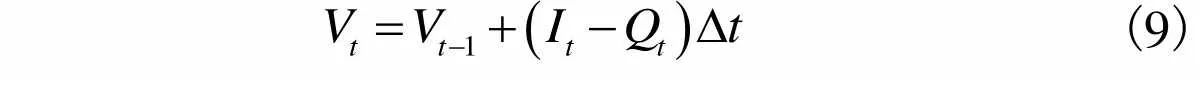
(9)

2 改进的IBR-SFLA

2.1 混合蛙跳算法

混合蛙跳算法(SFLA)是结合了确定性和随机性方法的基于群体智能的后启发式全局优化算法，该算法融合了模因演化和基于群体行为的粒子群算法的优点，具有参数少、理论概念易于理解等特点[5]．有关SFLA的更新和种群分组策略参阅文献[6]．

2.2 改进二进制编码混合蛙跳算法

2.2.1 青蛙子种群分组策略

传统SFLA分组策略首先将种群内各只青蛙按适应度好坏排序，此分组方式往往把适应相对较差的青蛙分在靠后的群组中，使得该组青蛙更新效率远不如前面的群组，导致青蛙的学习更新效果不佳．

为此，本文将整个蛙群划分为领导蛙、追随蛙、变异蛙3类蛙群，各类蛙群根据各自青蛙特点按相应更新机制进行迭代，从而提高更新效率．具体分组方法如下．

2.2.2 追随蛙蛙群局部搜索策略

图1 改进Sigmoid函数

Fig.1 Improved Sigmoid function

传统蛙跳算法中，子群中最差个体首先参照内部最优青蛙进行更新，若适应度无法提升，则根据全局最优青蛙进行更新；因而青蛙更新过程中并没有同时利用子种群、全局最优个体携带信息，导致蛙群子种群内部局部搜索机制存在局限性．本文对局部搜索方式进行改良，同时利用子种群内最优个体和全局最优个体来引导最差青蛙进行跳跃步长、觅食位置更新，其更新公式为

(11)

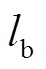
2.2.3 基于云模型的领头蛙蛙群精英进化策略

云模型可完成定性概念和定量描述间不确定转换，构建一种定量和定性间的映射，具有随机性和稳定倾向性的特点[7]．云模型的引入可在小范围内搜寻潜在的最优解，从而显著提升算法局部优化性能．

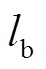
2.2.4 基于混沌理论变异蛙蛙群变异策略

变异蛙蛙群往往都是种群中较差个体，学习和交流能力远不如领导蛙和追随蛙蛙群，对此，本文根据混沌学理论遍历、随机、规律性等特征，运用改进后Logistic映射(式(12))生成混沌变量[9]，对青蛙进行混沌变异操作，在算法陷入迭代停滞时，在收敛域以外空间进行跳跃性“开拓”，寻找游离在可行域中的“有利突变”个体．

(12)

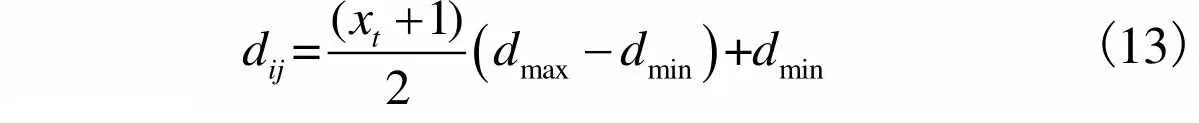
(13)

变异蛙更新后的位置如果优于当前全局范围内最优青蛙位置，原位置即被取代，若无法得到提升则保留原位置，继续按变异策略搜索直至触发终止条件.

2.3 改进的实数编码混合蛙跳算法

2.3.1 混沌理论初始种群生成机制

初始种群生成方式直接影响种群多样性和整体质量，相比随机生成的初始种群，利用第2.2节阐述的混沌原理遍历性、随机性进行蛙群初始化，可有效提升种群多样性、分布均匀性．

由于IR-SFLA优化变量为实数编码的机组负荷，因而对混沌变量映射到优化变量的方式进行调整，其公式为

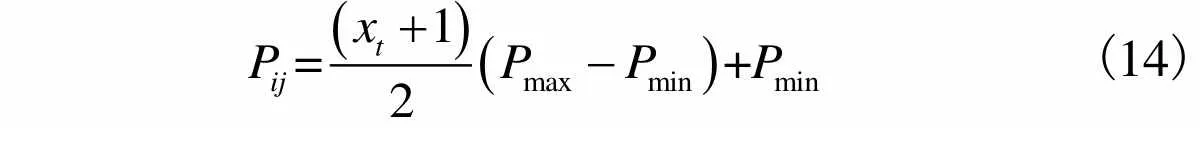
(14)

2.3.2 改进的局部搜索和位置更新策略

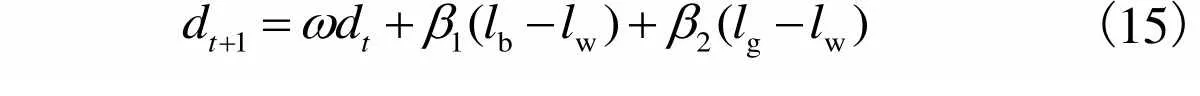
(15)

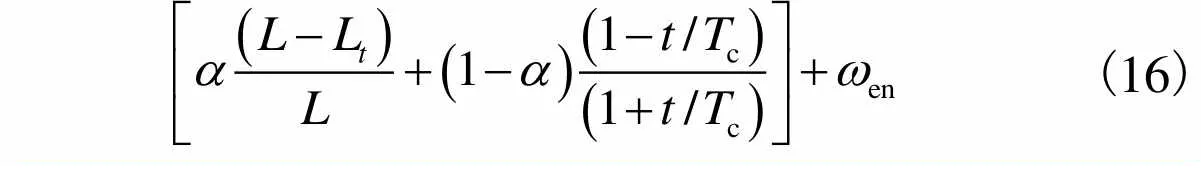
(16)

2.3.3 启发式青蛙激活机制

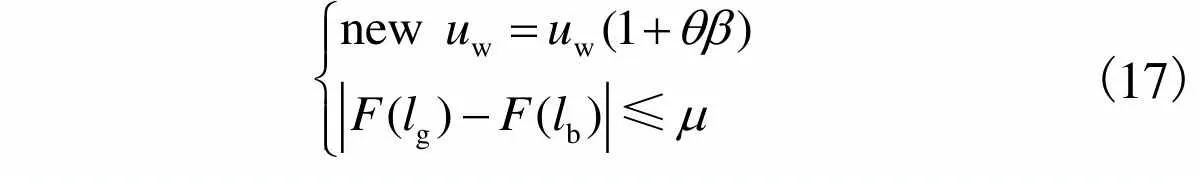
(17)

(18)

3 基于改进IBR-SFLA水电站短期发电调度模型

3.1 基于IB-SFLA的机组组合优化模型

将经济负荷分配模型与机组组合模型分别作为内、外层子模块，外层模块通过调用IR-SFLA制定的最优负荷分配表，对开启发电机组分配最优机组出力，进而计算相应总发电耗水量．内外层模块进行耗水量信息交流反馈，将信息传到UC子模块，利用提出IB-SFLA搜寻更优机组组合方式．详细模型优化流程如图2所示．

3.1.1 编码结构及初始化

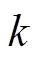
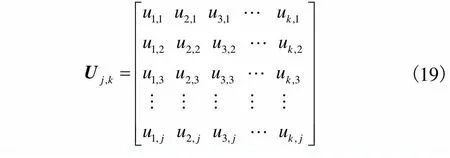
(19)

(20)

3.1.2 约束条件处理策略

1) 旋转备用约束修补策略

在某时刻机组组合方案确定后，需判定其是否满足旋转备用约束(见式(4))．若不满足需要启动备用容量补充方案，在启动额外机组满足旋转备用约束时，可能出现新增开机机组过多，导致备用容量偏大而额外增加一部分耗水量，此时需通过修复策略关闭部分机组．

引入机组启停优先顺序表来对合理安排机组启停时序，优先顺序表依照各类型机组在满负荷状态下的平均耗水率升序排列．机组满负荷耗水率[11](m³/MW)定义为

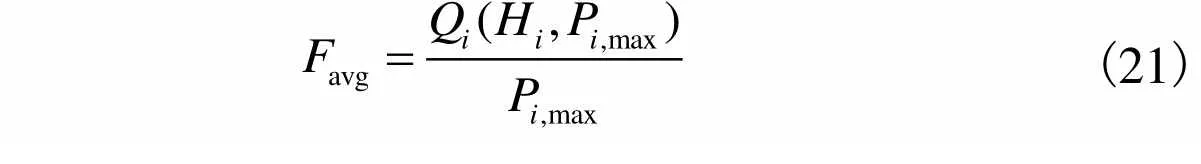
(21)

(1) 容量补充方案．当稳定运行条件下所有启动机组的总输出上限小于当时水电站的装载计划和备用容量之和时，以机组开启和关闭优先顺序，依次关闭已达到最小启动时间的机组，直到满足约束条件．

(2) 修复策略．当稳定运行条件下所有启动机组的最小输出总和大于当时水电站的装载计划和备用容量之和时，以机组启停优先顺序的相反顺序依次关闭满足最小启动时间的机组，直到满足系统备用容量约束．

2) 开启、关闭时间修补策略

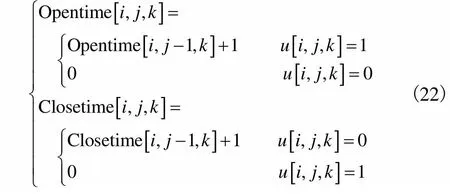
(22)

3.2 基于IR-SFLA经济负荷分配优化模型

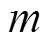
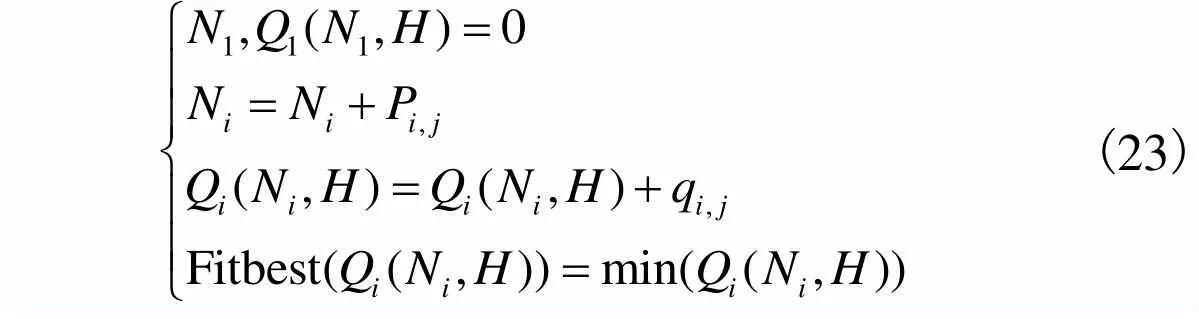
(23)

4 案例研究

4.1 三峡水电站STHGS研究

为验证IBR-SFLA在解决复杂、连续和离散空间优化耦合的STHGS问题的适用性和寻优性能，本文以三峡水电站大型发电机组短期发电优化为例，选取左、右岸26台发电机组，调度周期为24h．

4.1.1 算法主要参数设置

4.1.2 机组稳定运行区、发电负荷要求

不同机组流量特性曲线各有不同，在不同水头下都有各自稳定运行区，图3为75m、88m和107m平均水头下各类型机组(1#～26#)稳定、限制运行区的分布情况；水电站依照电力部门的用电计划，制定的发电机组各时段负荷要求如图4所示．

4.1.3 计算结果与讨论

针对三峡水电站26台发电机组在75m(低)、88m(中)和107m(高)平均水头下分别独立运算20次，机组分配负荷表、开启和关闭时序组合参见表1；图5为20次运算中最优发电耗水量的迭代曲线，描述了∶群中最优耗水量、平均耗水量迭代过程．

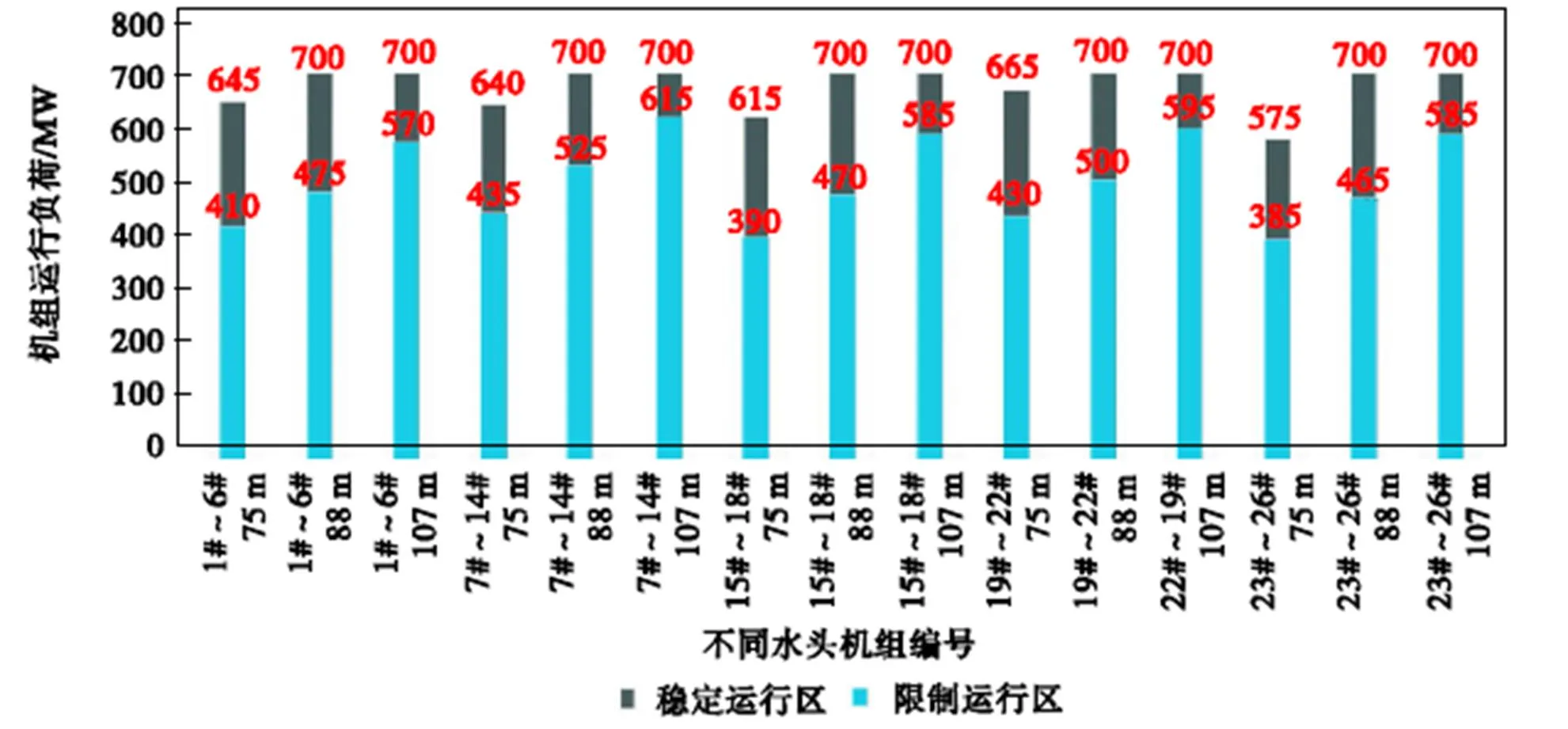
图3 各发电机组稳定、限制运行区

图4 机组各时段发电负荷要求

从图5可以看出，迭代初期IBR-SFLA在领头蛙蛙群领导下，算法依靠云模型在局部的深度搜索能力可以快速向最小耗水量不断逼近；与此同时追随蛙在改进搜索策略引导下不断向最小耗水量逼近；随着迭代深入，蛙群开拓能力开始下降，搜索可能趋于稳定停滞状态，即局部最优，变异蛙蛙群结合混沌理论随机性和遍历性特征，可在收敛停滞区域以外可行搜寻空间“开拓”更优解，有助蛙群及时跳出局部最优，摆脱“早熟”迹象，向更优耗水量收敛，而在迭代后期，IBR-SFLA稳定收敛到最优解．

表1 部分机组低水头各时段最优启停状态组合

Tab.1 Part of optimal unit commitment under the low water head

由表1可知，基于IBR-SFLA求解的机组短期发电调度经济负荷分配和机组组合可满足最小开启和关闭时间、禁止运行区域等约束；有效保证机组在各自稳定运行区运行，避免频繁启停对机组寿命的不利影响，实现发电机组安全高效运行．

为进一步验证IBR-SFLA在解决短期电力调度问题的高效性，选取改进遗传算法(LAGA)、扩展蚁群(EACO)、混沌引力搜索算法(CGSA)、烟花算法(FA)和改进蜂群算法(IBCO)作为对照，初始种群规 模和进化代数均保持一致，各方法独立运行20次，发电总耗水量迭代曲线如图6所示．

由图6可以看出，与对比算法相比，IBR-SFLA求解精度得到有效提升，可获取更小发电耗水量；LAGA收敛的最优解相对较差，与其交叉、变异参数不确定性有很大关联，IBR-SFLA需控制参数较少，一定程度降低算法不确定性；IBCO陷入搜索停滞状态时的局部深度“开拓”能力不如IBR-SFLA，导致其中后期搜索进程放缓，过早收敛到局部最优解．

图5 基于IBR-SFLA耗水量迭代曲线

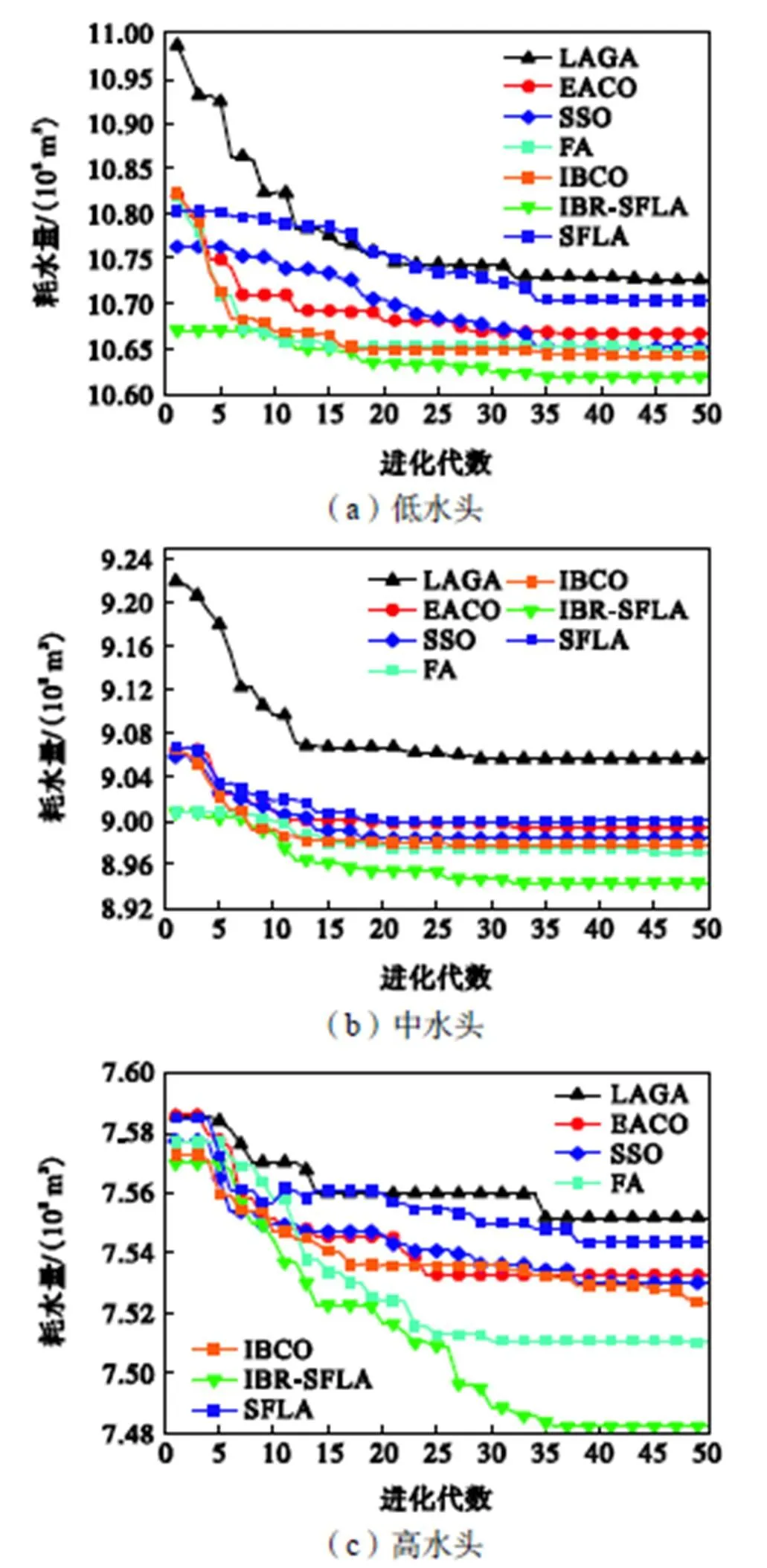
图6 IBR-SFLA与对比算法的发电耗水量迭代曲线

为进一步对比各算法结果的分布和离散情况，将3种水头下20次运行耗水量整理成箱形图(图7).图中各算法对应箱形图左侧为数据点，右侧为数据分布“箱子”．由图7可以看出，IBR-SFLA对应低、中和高水头的最优耗水量精度均优于其他算法，体现在IBR-SFLA获取的“箱子”位于最低位置；20次运行结果围绕中位数分布密集，离散程度较低，可由IBR-SFLA相对扁平的“箱子”和较短“胡须”(箱子上下的延伸线)验证，它表明IBR-SFLA在解决稳定性和准确性方面更加出色．对于高水头工况，虽然IBR-SFLA对应“箱子”高度并不占据优势，但其20次运算结果的分布位置均优于对比算法，较短的“胡须”表明不存在与中位数相距较远的“离群解”．

上述迭代曲线和箱形图验证了IBR-SFLA在求解精度和可靠性方面的高效性，但并未体现IBR- SFLA运算速度优势，IBR-SFLA整体性能(精度、可靠性和运算速度)优势如表2所示，表中“平均”、“最优”分别为20次运行平均和最优解．

分析表2数据可得以下结论．

(1)求解精度方面，IBR-SFLA相比LAGA、EACO、CGSA、FA以及IBCO有显著提升，以低水头为例，20次运行“平均”耗水缩减量分别为1.14×107、5.32×106、4.32×106、3.68×106和2.99×106m3，缩减率分别为1.06%、0.50%、0.40%、0.35%和0.28%，可以看出对SFLA的改进策略使得求解精度显著 提升．

(2) 求解速度方面，青蛙子种群只更新组内最差或最优青蛙，因而1次迭代可能只需计算1次，最多也只需3次运算，充分压缩每次迭代所需时间，提升算法寻优和收敛速度．

(3) 稳定可靠性方面，IBR-SFLA20次运行所得结果的标准差显著降低，图8中扁平的箱形图和较短的“胡须”表明解分布较为密集，离散程度较小，整体质量可得到保证，从而验证了IBR-SFLA良好的求解稳定性．

图7 基于IBR-SFLA和对比算法的耗水量箱形图(20次运行)

表2 IBR-SFLA与对比算法在3种水头下运行结果对比(20次运行)

Tab.2 Computational results of IBR-SFLA compared with other algorithms under three types of water heads(20 operations)

4.2 改进策略性能分析

为进一步验证种群规模、4种改进策略对算法性能的影响，体现本文方法的有效性和优势，设计了多组方案进行计算，各方案寻优过程、计算时间对比如图8所示．

从单一改进策略来看，4种策略较传统 SFLA均可不同程度改善短期发电调度耗水量；将各策略进行耦合所得优化结果最为明显．计算时间方面，加入改进策略的SFLA会有所增加，但增幅较小；从不同种群规模结果可知，改变种群规模对本文方法的提升有限，同时会显著增加计算时间．

综上所述，所提出的改进策略可有效地提高算法搜索性能，显著提升运行效率，在牺牲一定计算时间的前提下可获取更高质量的结果．

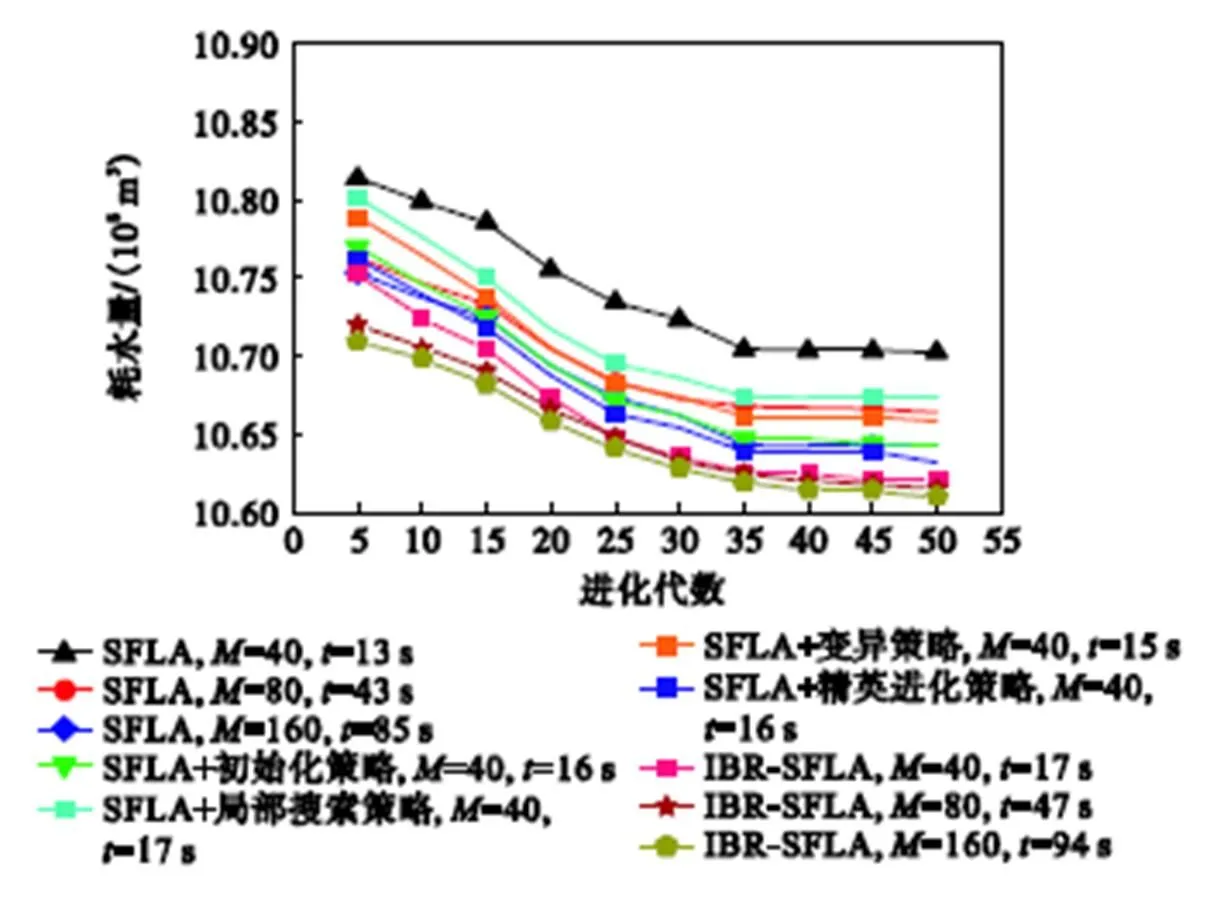
图8 不同方案下优化过程和运行时间对比(75m水头)

5 结 语

针对机组组合和经济负荷分配子问题组成的水电站短期发电调度问题，本文首先提出改进的二进制IB-SFLA和实数编码IR-SFLA，对于UC子问题，IB-SFLA将青蛙种群分组为3类，各类子种群基于云模型理论、改进的局部搜索公式、混沌学原理分别进行领头蛙、追随蛙和变异蛙蛙群的进化、更新、变异操作；经济负荷分配作为连续空间优化问题，由基于混沌理论的初始种群生成策略、改进的局部搜索与位置更新公式和启发式青蛙激活机制的IR-SFLA进行优化，进而提出基于二进制-实数编码IBR-SFLA方法．

改进后的IBR-SFLA应用到大规模机组短期电力调度优化问题，削减了水电站发电耗水量，实现水能资源高效利用；算法在保证运行稳定性前提下进一步提高求解精度，缩减运行时间，为STHGS优化问题提供切实有效新方法．

［1］ 石季英，薛 飞，李雅静，等. 基于免疫二进制萤火虫算法的主动配电网低碳目标网架规划[J]. 天津大学学报:自然科学与工程技术版，2017，50(5)：507-513.

Shi Jiying，Xue Fei，Li Yajing，et al. Active distribution system planning for low-carbon objective using immune binary firefly algorithm[J]. Journal of Tianjin Univer-sity：Science and Technology，2017，50(5)：507-513(in Chinese).

［2］ 沈冬梅. 基于改进引力搜索算法的电力系统机组组合问题的研究[D]. 上海：东华大学，2016.

Shen Dongmei. Research on Unit Commitment Problems in Power System Based on Improved Gravitational Search Algorithm[D]. Shanghai：Donghua University，2016(in Chinese).

［3］ Srikanth R K，Panwar L K，Kumar R，et al. Binary fireworks algorithm for profit based unit commitment(PBUC)problem[J]. International Journal of Electrical Power& Energy Systems，2016，83：270-282.

［4］ Hidalgo-P A，Vega-Rodríguez M A，Ferruz J，et al. MOSFLA-MRPP：Multi-objective shuffled frog-leaping algorithm applied to mobile robot path planning[J]. Engineering Applications of Artificial Intelligence，2015，44：123-136.

［5］ 赵付青，陈自豪. 基于自适应变异因子策略的混合蛙跳算法[J]. 甘肃科学学报，2016，28(1)：6-11.

Zhao Fuqing，Chen Zihao. Shuffled frog-leaping algorithm based on the theory of adaptive mutation factors[J]. Journal of Gansu Sciences，2016，28(1)：6-11(in Chinese).

［6］ 杨 哲，杨 侃，夏 怡，等. 考虑不同生态流量要求梯级水库群生态调度及其算法[J]. 天津大学学报：自然科学与工程技术版，2018，51(12)：1266-1277. Yang Zhe，Yang Kan，Xia Yi，et al. Optimal ecological operation of cascade reservoirs and the algorithm considering different ecological flow demand[J]. Journal of Tianjin University：Science and Technology，2018，51(12)：1266-1277(in Chinese).

［7］ 李德毅，孟海军，史雪梅. 隶属云和隶属云发生器[J]. 计算机研究与发展，1995，32(6)：15-20.

Li Deyi，Meng Haijun，Shi Xuemei. Membership clouds and membership cloud generators[J]. Journal of Computer Research and Development，1995，32(6)：15-20(in Chinese).

［8］ 黄海鹏，徐镇凯，李诒路. 基于云模型的河流健康多层次模糊综合诊断——以赣江南昌段为例[J]. 长江流域资源与环境，2015，24(增1)：62-69.

Huang Haipeng，Xu Zhenkai，Li Yilu. River health based on cloud model of multilevel fuzzy comprehensive diagnosis—In Nanchang section of ganjiang river[J]. Resources and Environment in the Yangtze Basin，2015，24(Suppl 1)：62-69(in Chinese).

［9］ 邹 强，王学敏，李安强，等. 基于并行混沌量子粒子群算法的梯级水库群防洪优化调度研究[J]. 水利学报，2016，47(8）：967-976.

Zou Qiang，Wang Xuemin，Li Anqiang，et al. Optimal operation of flood control for cascade reservoirs based on parallel chaotic quantum particle swarm optimization[J]. Journal of Hydraulic Engineering，2016，47(8)：967-976（in Chinese).

［10］ 滕志军，张晓旭. 基于惯性权重蛙跳算法的WSN布局优化[J]. 东北电力大学学报，2015，35(6)：66-69.

Teng Zhijun，Zhang Xiaoxu. The layout optimization of WSN based on inertia weight shuffled frog leaping algorithm[J]. Journal of Northeast Dianli University，2015，35(6)：66-69(in Chinese).

［11］ Lu P，Zhou J Z，Wang C，et al. Short-term hydro generation scheduling of Xiluodu and Xiangjiaba cascade hydropower stations using improved binary-real coded bee colony optimization algorithm[J]. Energy Conversion and Management，2015，91：19-31.

［12］ 吉 鹏，周建中，张 睿，等. 改进量子进化混合优化算法在溪洛渡电站机组组合中的应用研究[J]. 电力系统保护与控制，2014，42(4)：84-91.

Ji Peng，Zhou Jianzhong，Zhang Rui，et al. Study of unit commitment in Xiluodu based on a hybrid optimization algorithm of improved quantum evolution algorithm[J]. Power System Protection and Control，2014，42(4)：84-91(in Chinese).

Application of Short-Term Hydropower Generation Scheduling in a Hydropower Station Based on Improved Binary —Real-Coded Shuffled Frog Leaping Algorithm

Yang Zhe1，Yang Kan1，Wu Yun2，Xia Yi1，Qi Weiqing1，Zhang Tianyan1，Zhong Xiaolin3

(1. College of Hydrology and Water Resources，Hohai University，Nanjing 210098，China；2. Shanxi Conservancy Technical College，Yuncheng 044004，China；3. Yangzhou Survey Design Research Institute Co.，Ltd，Yangzhou 225000，China)

Short-term hydropower generation scheduling(STHGS)in a hydropower station is a complex multi-dimensional，non-linear optimization problem in non-continuous space with multiple constraints. The STHGS problem can be decomposed into unit commitment(UC)and economic load distribution(ELD)sub-problems. The traditional shuffled frog leaping algorithm(SFLA)has low efficiency on solution precision and reliability. This research focuses on incorporating the improved binary and real-coded SFLA into solving STHGS. The improved real-coded SFLA(IR-SFLA)and binary-coded SFLA(IB-SFLA)are applied to ELD and UC sub-problems，respectively. The IR-SFLA initializes the population with ergodicity and randomness in chaos theory and adopts renewed local search and location update strategies to realize frog evolution. In addition，the adaptive frog activation mechanism is introduced into reactive frog vitality during later iteration stage. In terms of IB-SFLA，the new frog grouping strategy tends to divide the frog population into leader，follower，and mutation frog sub-populations. Furthermore，each sub-population adopts the elite evolution strategy based on the normal cloud model as well as the improved local search pattern and frog mutation operation on basis of chaos theory to complete the iteration process. Overall，the final IBR-SFLA is established and applied to solve the STHGS problem. Comparison of the simulation results indicates that the IBR-SFLA can dramatically reduce the water consumption during power generation，with values of 1.14×107，1.22×107，and 7.52×106m3，corresponding to 75，88，and 107m water heads，and improve the utilization efficiency on hydropower resources. Moreover，with computational reliability and precision guaranteed，the maximum mean computation time reduction values are 178，173，and 172s. Furthermore，performance analysis indicates that the strategies can effectively enhance the search performance and improve the accuracy by increasing the computation time with a small amount. The high-quality solutions can be obtained at a small population size. Thus，the IBR-SFLA is verified to provide new basis to solve the STHGS problem in large hydropower stations.

short-term hydro generation scheduling(STHGS)in hydropower station；heuristic frog activation mechanism；improved sub-populations grouping strategies；elite evolution based on normal cloud model；frog mutation based on chaotic search

the Research and Extension Project of Hydraulic Science and Technology in Shanxi Province(No.2017DSW02)，the Science and Technology Project of Yunnan Water Resources Department，the National Basic Research Program of China (No.2012CB417006)，the National Science Support Plan Project of China (No. 2009BAC56B03).

TM612

A

0493-2137(2019)09-0979-11

2018-01-30；

2018-12-21.

杨 哲（1991—），男，博士研究生，zyang7279@hhu.edu.cn.

杨 侃，kyang@hhu.edu.cn.

山西省水利科学技术研究与推广资助项目(2017DSW02)；云南省水利厅科技资助项目；国家重点基础研究发展计划(973计划)资助项目(2012CB417006)；国家科技支撑计划资助项目(2009BAC56B03).

10.11784/tdxbz201801105

(责任编辑：孙立华)