基于自抗扰控制的永磁同步电机调速系统的研究
郑陆洋 傅惠南 余 雷 李 增
(广东工业大学机电工程学院,广东 广州 510006)
0 引言
永磁同步电机因结构简单、运行可靠、效率高、体积小等特点,在国防军工、工业伺服、电动汽车等诸多领域得到广泛应用。 但永磁同步电机是一个强耦合、参数时变、复杂的非线性系统[1],且在运行过程中易受环境、 外部负载干扰和其他未知因素的影响, 因此传统的PID 控制策略存在着不足和缺点。 自抗扰控制技术是中科院研究员韩京清提出的一种非线性控制理论,是在PID 控制基础上,引入了“安排过渡过程”和同时合理“提取微分信号”的方法,并加入扩张状态观测器对系统的未知模型和外部扰动总和作用量进行实时估计与补偿, 来改善控制器的性能, 在电机控制领域应用前景比较宽广[2]。
永磁同步电机的调速控制系统一般采用速度环、电流环闭环的串联结构。 电流环作为控制系统内环,其作用是对定子电流的准确与快速跟踪, 其控制效果好坏直接决定速度环的控制性能, 对整个控制系统而言作用重大; 转速环作为控制系统的外环, 其主要作用是对速度指令进行跟踪, 并输出电流作为电流环的输入, 它能够保证系统的抗干扰能力和快速响应性。目前而言, 在永磁同步电机矢量控制中, 通常在d-q同步旋转坐标系下建立永磁同步电机的数学模型,选用id=0 的控制方式进行解耦控制,控制过程简单。 但是当电流环采用PI 控制器控制时, 会出现电流波动大、抗扰能力差及稳定性不足等问题[3],速度环采用PI控制器,对负载变化的抗干扰能力减弱。 文献[4]中提出了采用模糊PID 控制器,可以解决参数实时整定问题,但模糊PID 控制器参数设置主要依靠经验, 且运行中计算量较大;文献[5]中提出采用滑模变结构的控制策略进行控制, 可以提高控制系统的响应速度和稳定性,但仍存在稳态误差。
本文以PI 控制的双闭环永磁同步电机矢量控制模型为基础, 采用自抗扰控制器代替速度环、 电流环的PI 控制器,使超调量减小,增强了抗扰能力,提高了控制性能。 通过仿真实验验证了该方法可行。
1 自抗扰控制器的分析与设计
1.1 自抗扰控制的分析
自抗扰控制器(active disturbance rejection controller,ADRC)是一种基于误差反馈的控制方法 ,不依赖于对象的精确数学模型; 主要由跟踪微分器、 扩张状态观测器和非线性状态误差反馈控制律三部分组成[6]。 跟踪微分器主要是安排过渡过程对输入信号进行跟踪并合理提取微分信号; 扩张状态观测器的作用是对系统未知模型的不确定部分和系统外部扰动的总和作用量进行实时估计并进行补偿, 从而使系统线性化为积分器串联型结构,简化了控制对象,提高控制性能;非线性状态误差反馈控制律是将安排过渡过程和扩张状态观测器的相应输出之间误差进行非线性组合, 它能使稳态误差以指数形式成数量级减小[7],以达到理想的控制效果。 为减少计算量、 降低复杂度, 采用一阶的ADRC。 一阶自抗扰控制的结构如图1 所示。
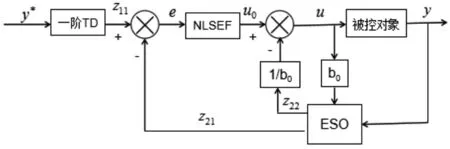
图1 一阶自抗扰控制的结构图
一阶自抗扰控制器三部分的具体实现形式如下:
被 控 对 象:
跟踪微分器
扩张状态观测器
非线性状态误差反馈控制律
式(1)-(4)中:x 是状态变量;u 为输入信号;y 是输出信号;y* 是期望输出信号;z11是y* 安排过渡后的跟踪信号;r 是非线性函数的时间尺度;z21和z22是扩张状态观测器对状态变量和扰动信号的观测值;β01、β02和β 是扩张状态观测器和非线性状态误差反馈控制律的参数;u0是扩张状态观测器输出的中间变量;b0补偿因子。 fal 函数是非线性函数,其具体形式为:

式 (5) 中:δ 决 定 该 函 数 线 性 区 间 长 度;α 为 该 函数 的 参 数,0 ﹤α ﹤1;sign 是 符 号 函 数。
1.2 速度环ADRC 的设计
永磁同步电机的机械运动方程为:
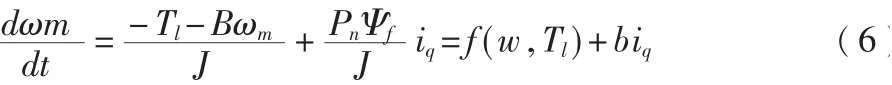
由式(6)可知速度环是一阶模型,因此速度环的自抗扰控制器为一阶的ADRC,其结构如图2 所示。

图2 速度环自抗扰控制器结构图
其中为ω* 是给定的速度信号,z11是安排过渡后的跟踪输出,z21和z22是扩张状态观测器的观测输出速度及系统扰动,u 是补偿后的输入信号,u0是非线性状态误差反馈控制律输出的控制信号。 速度环一阶自抗扰控制器的具体实现形式如下:
跟踪微分器:
扩张状态观测器
非线性状态误差反馈控制律
1.3 电流环ADRC 的设计
同步旋转坐标系下电机电流方程为:

由式(10)可知电流环为一阶模型,因此电流环的自抗扰控制器也为一阶的ADRC, 电流环处于控制系统的内环,电流的变化速度能够满足基本的控制要求,同时从设计原则的简单性和实用性来说,省略过渡环节,由于跟踪微分器省略,同时用比例环节来替代非线性误差反馈控制律。 电流环自抗扰控制的结构如图3 所示。

图3 电流环自抗扰控制器结构图
其具体实现形式为:
扩张状态观测器:
2 转速、电流双闭环永磁同步电机矢量控制模型的搭建
2.1 基于PI 控制的双闭环PMSM 模型的搭建
以永磁同步电机矢量控制[8]为基础,速度环与电流环均采用PI 控制, 搭建基于PI 控制的双闭环永磁同步电机控制系统如图4 所示, 模型主要由电机、坐标变换模块、SVPWM 模块、测量转换模块等部分组成。
2.2 基于ADRC 控制的双闭环PMSM 模型的搭建
采用自抗扰控制器代替永磁同步电机矢量控制系统中速度、电流环PI 控制器,在MATLAB/Simulink 中搭建系统仿真模型如图5 所示。
3 仿真结果对比分析
为验证本文所设计的基于ADRC 控制的双闭环PMSM 调速系统的控制效果,在Simulink 中进行仿真,电机的仿真参数设置为:定子电阻RS=0.958Ω;定子电感Ld=Lq=12mH; 磁链ψf=0.1827Wb; 转动惯量J=0.003kg·m2;阻尼系数B=0.008N·m·s;电机极对数Pn=4。
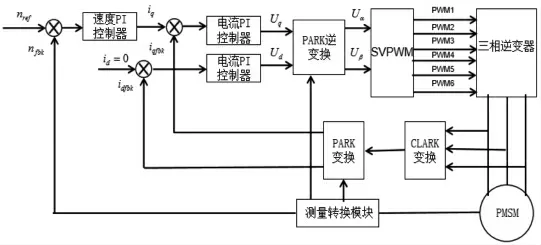
图4 基于PI 控制的PMSM 矢量控制图
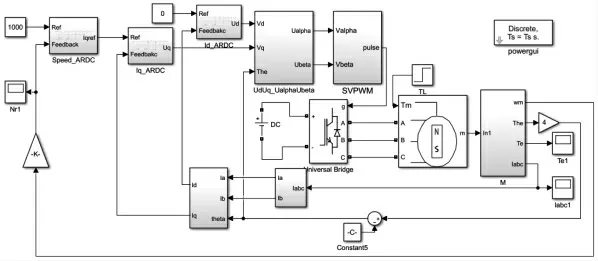
图5 基于ADRC 的双闭环PMSM 调速系统模型图
给定转速为1000r/min,初始负载为4N·m;在0.5s时负载阶跃到8N·m,系统仿真运行时间为1s,得到电机转速响应曲线、 转矩响应曲线及定子三相电流响应曲线比较如图6、图7、图8。

图6 电机转速响应曲线对
从图6 中可以看出, 采用ADRC 控制器的双闭环永磁同步电机调速系统与采用PI 控制器的双闭环永磁同步电机调速系统相比, 减小了超调, 抵抗负载变化的能力更强,两者达到稳定时间基本相同。
从图7 中可以看出, 采用ADRC 控制器的双闭环永磁同步电机调速系统与采用PI 控制器的双闭环永磁同步电机调速系统相比, 转矩波动小, 在负载变化时能够快速响应,抗干扰能力更强。
从图8 中可以看出, 采用ADRC 控制器的双闭环永磁同步电机调速系统与采用PI 控制器的双闭环永磁同步电机调速系统相比, 在启动时刻电流幅值变化较小, 意味着大电流对电机冲击更小, 二次波动幅值小,稳定性更好。

图7 电机转矩响应曲线对比图
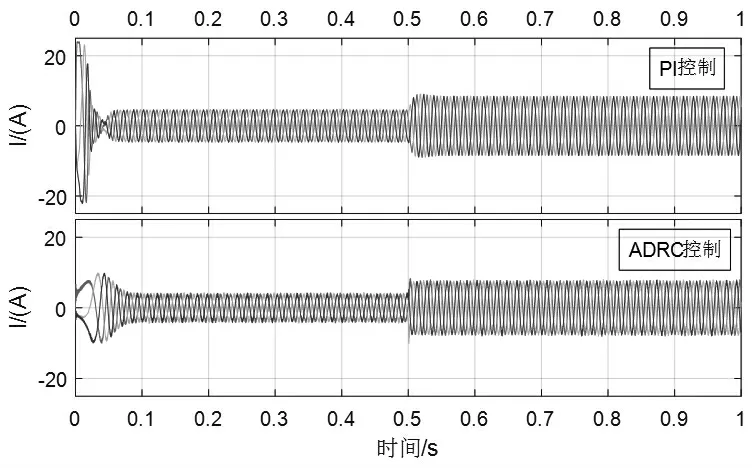
图8 电机定子三相电流响应曲线对比图
4 结语
根据上述的比较分析结果可知, 将自抗扰控制器应用到永磁同步电机速度环和电流环的控制中取代PI 控制器,能够减少超调量,增强控制系统的抗扰能力, 提高永磁同步电机的控制性能, 为工程实践应用提供了参考。

