种植土-碎石绿化带雨水入渗的数值分析

程树斌 张春会 关彤军 戴凌云 赵彦辉 马志中

摘要：為分析理论解析法求解种植土-碎石绿化带雨水入渗问题的合理性，建立了非饱和种植土-碎石绿化带雨水入渗的有限元模型，模型上边界设置储水表皮，模拟雨水入渗和积蓄，下边界为饱和排水，模型两侧不透水。首先，利用有限元模型模拟了均匀降雨条件下的雨水入渗特征，与理论解析解对比，验证了模型的正确性。然后，利用有限元模型计算石家庄市2年重现期3 h设计暴雨雨型条件下种植土的雨水入渗，地表开始积水时间、降雨结束后积水深度、雨量径流系数分别为075 h，13.6 cm和0.24，均匀降雨理论解析解计算结果分别为0.72 h，14.4 cm和0.17，两种方法计算结果相差不多。再次，利用有限元模型计算了下边界孔压变化、上边界孔压变化条件下的种植土地表开始积水时间，结果表明随着下边界孔压降低，地表开始积水时间延长，随着上边界孔压降低，地表开始积水时间延长，当下边界孔压为0 kPa时，初始上边界孔压分别为-6 kPa和-12 kPa，地表开始积水时间分别为45 min和50 min，地表开始积水时间有一定差异;当初始上边界为-6 kPa，下边界分别为0 kPa，-1 kPa，-2 kPa和-3 kPa时，地表开始积水时间分别为45 min，45 min，46 min和47 min，下边界条件对地表开始积水时间影响较小。地基土渗透系数为6.5×10-9 m/s，地基土孔隙水压力分别为0 kPa，-4.5 kPa，-9 kPa，-13.5 kPa和-18 kPa，利用有限元模型求解获得种植土地表开始积水时间分别为54 min，54 min，55 min，55 min和56 min，地表积水深度分别为11.9 cm，11.7 cm，11.5 cm，11.4 cm和11.3 cm，随着地基土孔隙水压力降低，种植土地表开始积水时间略有延长，种植土地表积水深度略有降低，总体上地基土孔隙水压力对种植土地表积水时间和积水深度影响不大。地基土孔隙水压力0 kPa，渗透系数分别为6.5×10-9 m/s和6.5×10-7 m/s，利用有限元模型计算获得种植土地表开始积水时间均为54 min，积水深度均为119 cm，地基土渗透系数对种植土地表积水时间和积水深度基本无影响。从上述研究结果可以看出，可以使用平均降雨强度和理论解析法计算地表开始积水时间和积水深度;下边界条件对地表开始积水时间和积水深度影响不大;地基土的饱水渗透系数、地基土的初始含水率对地表积水开始时间和地表积水深度影响不大;使用理论解析解求解种植土-碎石绿化带雨水入渗问题是合理的。

关键词：城市给水排水工程;种植土-碎石绿化带;有限元模型;边界条件;雨型

中图分类号：TU443文献标志码：A

CHENG Shubin， ZHANG Chunhui， GUAN Tongjun， et al.Numerical modeling to rainfall infiltration into planting-soil-crushed-stone green belt[J].Journal of Hebei University of Science and Technology，2019，40（1）：79-85.Numerical modeling to rainfall infiltration into

planting-soil-crushed-stone green belt

CHENG Shubin1，2， ZHANG Chunhui2，3， GUAN Tongjun2， DAI Lingyun3， ZHAO Yanhui2， MA Zhizhong2

（1.Shijiazhuang Municipal Construction Management Office， Shijiazhuang， Hebei 050000， China; 2.Shijiazhuang Municipal Design & Research Co.， Ltd.， Shijiazhuang， Hebei 050000， China;3.School of Civil Engineering， Hebei University of Science and Technology， Shijiazhuang， Hebei 050018， China）

Abstract：To verify the rationality of the theoretical analytical method to solve the rainfall infiltration into planting-soil-crushed-stone green belt， the finite element model of the rainfall infiltration into unsaturated planting soil is established. The water storage skin is used to model the infiltration and accumulation of rainwater on the upper boundary of the model. The lower boundary is saturated and drained， and the both sides of the model are impervious. Firstly， the infiltration characteristics of road rainwater under uniform rainfall conditions are modeled by the finite element model. Compared with the theoretical analytical solution， the finite element model is proved to be right. Secondly， the infiltration of road rainwater into planted soils is calculated by the finite element model under the condition of 2-year recurrence period and 3-hour design rainstorm of Shijiazhuang city. The beginning time of the surface water， the rainwater depth of stopping rainfall and the coefficient of rainfall runoff are 0.75 h， 13.6 cm and 0.24， respectively. The analytical results of uniform rainfall method are 0.72 h， 14.4 cm and 017， respectively. The results of the both methods are basically identical. Thirdly， the finite element model is employed to calculate the beginning time of the surface water under the condition of different pore pressure at the lower boundary and upper boundary. The results show that with the pore pressure descending at the lower boundary， the beginning time of the surface water rises up. With the pore pressure dropping at the upper boundary， the beginning time of the surface water increases. When the pore water pressure is 0 kPa at the lower boundary and the initial pore water pressure at the upper boundary are -6 and -12 kPa， the beginning time of the surface water are 45 and 50 min， respectively. Obviously the beginning time of the surface water is different. When the initial pore water pressure is -6 kPa at the upper boundary and the pore water pressure at the lower boundary are 0， -1， -2 and -3 kPa， the beginning time of the surface water are 45， 45， 46 and 47 min， respectively. The lower boundary condition has little effects on the beginning time of the surface water. When the permeability coefficient is 6.5×10-9 m/s and the pore water pressure of ground soil are 0， -4.5， -9， -13.5 and-18 kPa， the finite element model is used and the beginning time of the surface water are 54， 54， 55， 55 and 56 min， respectively. Correspondingly the surface water depths are 11.9， 11.7， 11.5， 11.4 and 11.3 cm， respectively. With the pore water pressure in ground soil decreases， the beginning time of the surface water slightly increases， and the surface water depth descends. As a whole， the pore water pressure in ground soil has little effect on the beginning time and the depth of the surface water. When the pore water pressure in ground soil is 0 kPa and the permeability coefficients are 6.5×10-9 and 6.5×10-7 m/s， the beginning time and the depth of the surface water by the finite element model are 54 and 11.9 cm， respectively. The permeability coefficient of the ground soil has little effect. Based on above analysis， our main conclusions are： Uniform rainfall intensity and theoretical analytical method can be used to calculate the beginning time and the depth of the surface water. The lower boundary condition has little effects on the beginning time of the surface water and water depth. The saturated permeability coefficient and the initial water content of the ground soil have no significant influence on the beginning time of the surface water and water depth. It is recommended to employ the analytical solution to analyze the rainwater infiltration in to planting-soil-crushed-stone green belt.

Keywords：city water supply and sewage engineering; planting-soil-crushed-stone green belt; finite element model; boundary conditions; rainfall pattern

河北科技大学学报2019年第1期程树斌，等：种植土-碎石绿化带雨水入渗的数值分析为改善城市生态环境，减轻城市热岛效应和内涝灾害，2014年住房和城乡建设部发布了《海绵城市建设技术指南》[1]，鼓励中国各个城市建设海绵城市。2015年，迁安[2]、镇江[3]、南宁[4]等16个城市入选海绵城市建设试点城市。海绵城市建设技术已为国内外学者广泛关注。在海绵城市建设技术方面，美国率先提出了低影响开发的概念（low influence development），随后一些国外学者先后研究了低影响开发建设技术[5-8]。中国学者也先后对透水路面、植草沟、雨水花园、生物滞留带、下凹式绿地等海绵城市结构设施开展了研究[9-14]。近些年，随着海绵城市建設工程的实践还出现了许多新的海绵城市结构和海绵道路结构，种植土绿化带就是其中一种。种植土绿化带海绵道路结构的工作原理为[20]机动车道为不透水沥青路面，雨水沿横坡汇流至下凹绿化带内，经种植土入渗至碎石储层内，再逐渐入渗至地基土内。程树斌等[20]取种植土为研究对象，将种植土绿化带雨水入渗视作非饱和一维问题，假设降雨均匀，下边界为饱和排水边界，进而利用拉普拉斯变化给出了种植土雨水入渗的计算方法。程树斌等给出的理论解为[20]K=qB-（qB-eαψ0）e-z-4（qB-qA）e（L-z）/2e-t/4M，（1）式中，M=∑∞n=1sin（λnz）sin（λnL）e-λ2nt1+（L/2）+2λ2nL;λn为如下超越方程的正值解，即tan（λL）+2λ=0;K为相对渗透系数，K=K0（Ψ）/Ks，K0（Ψ）为孔压Ψ时非饱和土渗透系数，Ks为饱和渗透系数;qA=qA0/Ks;qB=qB0/Ks，qA0为初始条件调整降雨强度，qB0为种植土上边界降雨强度;Ψ0为种植土下边界孔压，一般取为0;α为种植土孔压与体积含水率之间负指数函数关系的拟合系数;L，z和t分别为种植土无量纲厚度、坐标和时间，具体表达式参考文献[20]。

利用式（1）求解均匀降雨条件下种植土内的孔压演化，然后采用种植土孔压曲线正、负孔压包络面积代数和为0的方法求得地表开始积水时间（即种植土饱和的时间）[20]，进而可计算种植土绿化带降雨历时内地表积水深度、雨量径流系数、下凹绿地深度等设计参数。

然而，在利用公式（1）求解地表积水时间时，尚有几个疑问需要厘清：

1）利用式（1）求解地表积水时间时，假设降雨量在降雨历时内均匀分布，没有考虑雨型的影响，然而实际降雨是非均匀的，这种假设是否对计算结果有影响？

2）种植土下边界含水率是变化的，在分析中一般简化为饱和排水边界，这是否对计算结果有影响？

3）式（1）求解中，仅研究了种植土，没有考虑碎石层、地基土含水率和渗透系数的影响，这是否对计算结果有影响？

为了明晰上述问题，本文在Geo-Studio2012[21]下建立了种植土绿化带雨水入渗的有限元数值模型，分析了雨型、种植土下边界条件和地基土特性对种植土绿化带雨水入渗的影响。

1数值模拟

1.1种植土雨水入渗有限元模型

本文算例由石家庄市汇明路种植土绿化带工程概化而成，其结构如图1所示。取种植土进行研究。种植土纵向长度远大于横向，可视为平面应变问题。种植土宽度为2.4 m，厚度为0.6 m，种植土下边界为饱和排水边界，上边界为流量边界，其值为降雨强度。以种植土下边界中心为原点，向上为正，坐标系如图1所示。

种植土的初始条件如下：下边界孔压为0 kPa，上边界孔压为-6 kPa。左、右两侧均为不透水边界。种植土的饱水渗透系数为1.0 cm/h （即2.78×10-6 m/s），饱和体积含水率为0.48，残余体积含水率为0.11，α=0167 kPa-1（或0016 7 cm-1）。

为模拟雨水在地表的积蓄，在地表设置了储水表皮[21]。

考虑机动车道雨水汇集至种植土绿化带，绿化带等效降雨强度qe为[20]qe=q（1+ψeAy+A0Al）=qη，（2）式中：q为降雨强度;Ay为机动车道宽度;Al为绿化带净宽，ψe为雨量径流系数;A0为绿化带被混凝土占据的宽度。本文汇明路工程中，Ay=7.5 m，Al=2.4 m，A0=0.6 m，ψe=0.9，η=4.06。建立的数值模型如图2所示。

1.2数值模型验证

为验证建立的数值模型的正确性，取如下降雨进行分析：暴雨均匀持续24 h，总降雨量为55.7 mm，等效降雨强度qe=9.42 mm/h。利用2.1中的有限元模型求解。

另外，使用解析解式（1）进行求解，λn值取12项，分别为[20]1.836 6，4.815 8，7.917 1，11.040 8，14.172 4，17.307 6，20.444 8，23.583 1， 26.722 2，29.861，33.001 9，36.142 1。

种植土内孔压随时间演化规律的有限元模型解和解析解结果如图3所示。图3中，T为实际入渗时间，Z*为真实竖向坐标，参考图1。从图3可以看出，本文数值解与解析解结果基本一致，这表明本文数值模型是正确的。

从图3可以看出，在初始状态，种植土非饱和，土体内孔压为负，从地表向下孔压近似线性增加。随着雨水入渗，近地表的孔压增大。随降雨时间增加，从地表向下孔压不断增加，并逐步趋于饱水。

1.3雨型对种植土地表开始积水时间的影响

石家庄市2年重现期3h设计暴雨历时曲线如图4所示，其3 h累计降雨量为46.4 mm。

等效降雨强度是对图4所示的设计暴雨历时曲线增大4.06倍，结果如图4所示，等效降雨量为188.4 mm。按图4等效降雨强度历时曲线进行计算，获得种植土内孔压演化如图5所示。

从图5可以看出，随着降雨，种植土饱和度快速增长。当降雨45 min左右（约0.75 h），地表开始积水，3 h降雨结束后，地表积水接近13.6 cm。若植物耐水湿时间为12 h，降雨结束后，还可允许入渗9.75 h，入渗雨水975 cm，因此下凹绿化带深度不宜超过9 cm，以避免在这种降雨条件下绿化带内植物浸泡时间过长而枯萎。

若积水深度为9 cm，则溢流4.6 cm，流量径流系数为46/188.4=0.24。

利用公式（1），使用平均降雨强度计算，等效平均降雨强度为188.4/3=62.8 mm/h，其地表开始积水时间为0.7 h，按植物耐水湿时间12 h考虑，下凹绿化带深度可为9.7cm，取为9 cm。入渗雨量为62.8×0.7+2.3×10+10×9=156.96 mm，溢流31.4 mm，流量径流系数为31.4/188.4=0.17。

对比有限元模型解和解析解可以看出，两种方法得到的地表开始积水时间和流量径流系数相差不多，这表明雨型对解析解计算的地表开始积水时间、降雨结束后积水深度、雨量径流系数等的计算结果影响不大。

1.4下边界条件对地表开始积水时间的影响

使用理论解析解（即公式（1））计算中，一般将下边界简化为饱和排水边界，这种简化是否合理呢？

实际上，理论解析解中下边界条件可根据下边界含水率确定。然而，降雨入渗后下边界较湿润，甚至饱和。降雨停止，种植土内水分也逐渐入渗，通过下边界进入碎石层，下边界含水率仍然很大。若碎石层内有积水，蒸发气化也使得种植土下边界含水率较高。因此，从定性上来看，将下边界视作饱和排水边界进行计算有一定道理，计算结果稍有保守，下面进行定量分析。

变化初始上边界和下边界条件，按表1所示6种工况，使用本文数值模型计算，获得了上（初始）、下边界为不同负孔隙水压力（或含水率）情况下地表开始积水时间，结果如表1所示。

从表1可见，当下边界为饱和排水边界（工况1和5）、初始上边界条件不同时，地表开始积水时间分别为45 min和50 min，地表开始积水时间有一定差异。当初始上边界条件相同（如工况1、工况2、工况3、工况4），下边界条件改变时，地表开始积水时间在45～47 min之间，下边界条件对地表开始积水时间没有显著影响。

因此，在使用理论解析公式（1）计算地表开始积水时间时，种植土下边界取为饱和排水边界，对计算结果没有显著影响。

1.5地基土性质对种植土地表开始积水时间的影响

首先建立种植土-碎石层-地基土的海绵道路结构雨水入渗模型。

种植土的物理及水力学特性参数如21和2.3所示。初始上边界的孔压为-12 kPa，上边界条件为雨量边界条件，其值为图4所示的等效降雨强度。不指定下边界条件，下边界直接与碎石层相接。

碎石层厚度为0.75 m，孔隙度为0.4，饱和体积含水率为0.4，α=1.55 kPa-1，残余体积含水率为0.08，饱和渗透系数为3×10-4 m/s。

碎石层下为地基土，地基土α为0.032 kPa-1。饱和体积含水率为0.43，残余体积含水率为0.28。地基土的工况如下：初始孔隙水压力分别为0，-4.5，-9，-13.5，-18 kPa，地基土的饱水渗透系数分别为6.5×10-9 m/s和1.0×10-6 m/s，共10种工况。

地基土计算区域尺寸为50 m×25 m，计算域足够大。地基土除与碎石层接触界面外的边界均为不透水。种植土和碎石层位于地基土表面正中央。

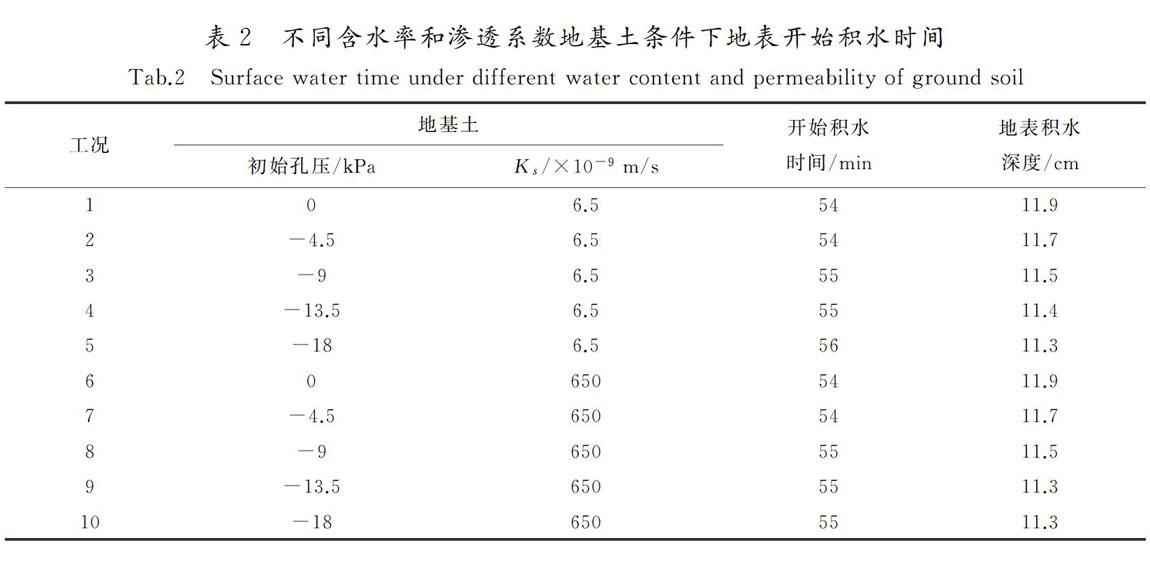
利用建立的有限元模型进行计算，获得不同工况地表开始积水时间和积水深度如表2所示。

从表2可以看出，渗透系数相同（如6.5×10-9 m/s）条件下，不同初始孔压（或饱和度）地基土地表开始积水时间在54～55 min之间，降雨结束后地表积水高度在11.3～11.9 cm之间，地基土初始孔压对种植土地表开始积水时间和降雨结束后的地表积水高度都影响微小。地基土的渗透系数增加100倍，若地基土初始孔压相同，种植土地表开始积水时间和降雨结束后的地表积水高度都基本没有影响。

可见，地基土的含水率（初始孔压或饱和度）和地基土的饱水渗透系数对种植土地表开始积水时间和降雨结束后积水高度基本无影响。

从前述数值模拟结果可以看出：使用平均降雨强度和理论解析公式（1）计算地表开始积水时间和积水深度与考虑雨型的有限元计算结果差别不大;下边界条件对地表开始积水时间和积水深度影响不大;地基土的饱水渗透系数、地基土的初始含水率对地表积水开始时间、地表积水深度影响不大。

可见，使用理论解析公式（1）计算降雨條件下种植土的地表开始积水时间是完全可行的。

2设计的计算方法

前述研究结果表明，使用理论解析公式（1）可以计算降雨条件下地表开始积水时间，进而可以计算种植土绿化带工程中的一些关键设计参数，具体实现过程如下：

1）将设计降雨雨型的降雨量在降雨历时内平均，作为设计降雨强度，然后利用公式（2）求解等效降雨强度qe;

2）利用理论解析公式（1）和等效降雨强度计算不同时间的种植土内孔隙水压力分布图;

3）计算不同时间孔隙水压力分布图的面积代数和，当分布图的面积代数和为0时，对应的时刻即为地表开始积水时间。若地表开始积水时间为T0，稳定入渗时间[20]为T1，则降雨结束时种植土入渗雨水的高度H0为H0=qeT0+KsT1。（3）若在降雨历时内不能入渗的雨水，全部通过径流排走，则雨量径流系数可以表示为λ=qe（T0+T1）-H0-H3qe（T0+T1）。（4）式中，H3为种植土下凹绿化带深度。

若没有雨水排走，则绿化带需要下凹，以储存来不及入渗的雨水。若绿化带内植物的耐水湿时间为T2，则下凹绿化带设计深度为H3=（T2-T1）Ks。（5）

3结论

本文在GeoStudio2012中分别建立了种植土、种植土-碎石-地基土的绿化带雨水入渗有限元模型，分析了雨型、种植土下边界条件、地基土含水率和渗透性对地表开始积水时间和积水深度的影响，获得了如下结论：

1）使用平均降雨强度和理论解析公式（1）计算地表开始积水时间和积水深度与考虑雨型的有限元计算结果差别不大。

2）下边界条件对地表开始积水时间和积水深度影响不大。

3）地基土的饱水渗透系数、地基土的初始含水率对地表积水开始时间和地表积水深度影响不大。

4）可以利用理论解析公式（1）计算种植土的地表开始积水时间。

5）式（3）—式（5）可用于计算雨量径流系数、下凹绿化带深度。

参考文献/References：

[1]住房和城乡建设部. 海绵城市建设技术指南[S].2014.

[2]王雪，严军，俞仲春，等.迁安市既有小区广场馨园海绵城市设计策略[J].中国给水排水，2018，34（8）：1-4.

WANG Xue，YAN Jun，YU Zhongchun，et al. Design strategy of sponge city in Qian'an city： Taking the square Xinyuan as an example[J].China Water & Wastewater，2018，34（8）：1-4.

[3]绪涛，周绪旭，张旭伟，等.镇江海绵城市建设工程质量监督管理研究[J].工程质量，2018，36（9）：17-20.

XU Tao，ZHOU Xuxu，ZHANG Xuwei， et al.Research on the quality supervision and management of Zhenjiang sponge city construction[J].Construction Quality，2018，36（9）：17-20.

[4]吴珊，彭定仕，苏拥军，等.海绵城市设计方案及模拟论证——以南宁心圩车辆段为例[J].水科学与工程技术，2018（4）：42-46

WU Shan，PENG Dingshi，SU Yongjun，et al.Sponge city design plan and simulation——taking Xinyu depot in Nanning for example[J].Water Sciences and Engineering Technology，2018（4）：42-46.

[5]DREELIN E A， FOWLER L，CARROLL C R. A test of porous pavement effectiveness on clay soils during natural storm events[J]. Water Research，2006，40： 799-805.

[6]COLLINS K A，HUNT W F，HATHAWAY J M. Hydrologic comparison off our types of permeable pavement and standard asphalt in Eastern North Carolina[J]. Journal of Hydrologic Engineering ，2008，12（13）： 1146-1157.

[7]DEBUSK K M，WYNN T M.Storm-water bioretention for runoff quality and quantity mitigation[J]. Journal of Environmental Engineering，2011，137（9） ：800-808.

[8]LIN Chai， MASOUD K， BRANDON G， et al. Hydraulic performance of fully permeable highway shoulder for storm water runoff management[J]. Journal of Environmental Engineering， 2012，138（7）：711-722.

[9]吴礼舟，张利民，黄润秋.成层非饱和土渗流的耦合解析解[J].岩土力学，2011，32（8）：2391-2396.

WU Lizhou， ZHANG Limin， HUANG Runqiu. Analytic solution to coupled seepage in layered unsaturated soils[J].Rock and Soil Mechanics， 2011，137（9） ：800-808.

[10]宮永伟，戚海军，李俊奇， 等.城市道路低影响开发设计的雨洪滞蓄效果分析[J].中国给水排水，2014， 30（9）： 151-158.

GONG Yongwei， QI Haijun， LI Junqi， et al. Retention and reduction of rainwater on urban roads based on low impact development[J]. China Water & Waste Water， 2014， 30（9）：151-158.

[11]唐雙成，罗纨，贾忠华，等.填料及降雨特征对雨水花园削减径流及实现海绵城市建设目标的影响[J]. 水土保持学报，2016，30（1）：73-78.

TANG Shuangcheng， LUO Wan， JIA Zhonghua， et al. Effects of filler and rainfall characteristics on runoff reduction of rain garden and achieving the goal of sponge city construction[J].Journal of Soil and Water Conservation， 2016，30（1）：73-78.

[12]顾天奇，张古陶，孙海洋，等.新建开发区海绵城市实践-以苏州太湖新城市政道路生态雨水渗透及利用工程为例[J].中国市政工程，2016（2）：30-32.

GU Tianqi， ZHANG Gutao， SUN Haiyang， et al. Sponge city practice in new-built development zone： taking municipal road ecological rainwater infiltration & recycling project in Suzhou Taihu new city as an example[J].China Municipal Engineering， 2016（2）：30-32.

[13]车伍，赵杨，李俊奇，等. 海绵城市建设指南解读之基本概念与综合目标[J].中国给水排水， 2015，31（8）：1-5.

CHE Wu， ZHAO Yang， LI Junqi， et al. Explanation of sponge city development technical guide： Basic concepts and comprehensive goals[J]. China Water & Waste Water， 2015，31（8）：1-5.

[14]]陈朗，麦天鹏，张腾璨.海绵城市工程措施在城市景观广场的综合运用[J].城市道桥与防洪，2018（9）：70-72.

CHEN Lang，MAI Tianpeng， ZHANG Tengcan. Comprehensive application of sponge city engineering measures in urban landscape square[J].Urban Roads Bridges & Flood Control，2018（9）：70-72.

[15]张亮.西北地区海绵城市建设路径探索——以西咸新区为例[J].城市规划，2016，40（3）：108-112.

ZHANG Liang. Path of sponge city construction in northwestern China： An empirical study on Xixian new area[J].City Planning Review，2016，40（3）：108-112.

[16]中华人民共和国国家标准.建筑与小区雨水利用工程技术规范（GB50400—2006）[S].

[17]中华人民共和国行业标准.透水沥青路面技术规程（CJJ/T 190—2012）[S].

[18]中华人民共和国行业标准.透水水泥混凝土路面技术规程（CJJ/T 135—2009）[S].

[19]中华人民共和国行业标准.透水砖路面技术规程（CJJ/T 188—2012）[S].

[20]程树斌，关彤军，张春会，等.海绵城市道路种植土-碎石绿化带的雨水入渗[J].中外公路， 2018， ，38（2）：13-19.

CHENG Shubin，GUAN Tongjun，ZHANG Chunhui， et al. Rainfall infiltration of road planting soil-green vegetative macadam belt in sponge city[J]Journal of China & Foreign Highway，2018，38（2）：13-19.

[21]GEO-SLOPE International Ltd. Seepage Modeling with SEEP/W[EB/OL].http：//www.lulu.com/gb/en/shop/geo-slope-international/seepage-modeling-with-seepw/paperback/product-21672549.html，2014-06-13.第40卷第1期河北科技大学学报Vol.40，No.1

2019年2月Journal of Hebei University of Science and TechnologyFeb. 2019