依赖密度的Boussinesq方程组的局部强解的存在唯一性
侯 伟 李兴利 赵成元
(枣庄科技职业学院, 山东 滕州 277500)
1 引言及主要结论
Boussinesq方程组是流体方程中一类重要的方程.本文主要考虑如下非齐次不可压Boussinesq方程组的初边值问题:
(1.1)
上面方程组中,Ω⊆R3是有界并且边界光滑的区域,研究的流体速度函数定义为u=u(x,t),温度函数、密度函数、压力函数定义为θ=θ(x,t).定义在外力作用下的向量函数f=f(x,t),并且已知初始速度u=u0(x),初始动量ρ0u0=ρ0u0(x).这里Cv,μ,κ均为θ的正的函数,Cv、μ、κ分别表示比热容、流体粘性系数、热传导系数.
近年来,有关Boussinesq方程组的研究有了新的进展.1999年,Kageir证明了三维粘性Boussinesq方程组弱解的整体存在性[1].另外,李现今[2]在2010年又证明了三维Boussinesq方程组大解的全局L2稳定性.
本文研究依赖ρ的三维Boussinesq方程组强解的局部存在唯一性.
定理1.1设Ω⊆R3为边界光滑的有界开区域,T是一个正常数,假设(ρ0,u0,θ0,f)满足正则条件:

若(ρ,u,p,θ)满足下面的条件:
(1.2)
这里(g1,g2)∈L2(Ω),P0∈H1(Ω)而且系数满足:
0<μ,CV,k∈C1(R2),μ=μ(ρ,ρθ),
那么初边值问题(1.1)存在唯一的局部强解(ρ,u,p,θ)满足:
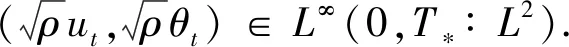
(1.3)
其中T*>0是某常数.
2 解的一致估计
为了证明定理1.1,考虑线性问题:
(2.1)
这里记:
μ∶=μ(ρ,ρη),Cv∶=CV(ρ,ρη),k∶=k(ρ,ρη),μ0∶=μ(ρ0,ρ0θ0),k0∶=k(ρ0,ρ0θ0)
假定初值(ρ0,u0,θ0)满足:

(2.2)
q∈[3,6],(g1,g2)∈L2(Ω),p0∈H1(Ω),f∈H1(Ω×(0,T)),ft∈L2(0,T;L2(Ω)). 假定已知向量对(v,η)满足:
(v,η)∈C([0,T];H2(Ω))∩L2(0,T;W2,q(Ω)),(vt,ηt)∈L2(0,T;H1(Ω)).
(2.3)
divv=0,v|∂Ω=0,η·n|∂Ω=0
引理2.1
(2.11)
(2.12)
(2.13)

可以得到结论:
(2.14)
(2.15)
(2.16)

(2.17)
定理2.1假定(v,η)满足(2.3),用T*代替T且(v(0),η(0))=(u0,θ0),

(2.18)
那么线性问题(2.1)在[0,T*]存在唯一的强解(ρ,u,p,θ)满足估计(2.14)-(2.17),而且有下面的正则性:
ρ∈C([0,T*];W1.q),ρt∈C([0,T*];Lq),(u,θ)∈C([0,T*];H2)∩L2(0,T*;W2,q),
p∈C([0,T*];H1)∩L2(0,T*;H-1.q),
因为证明过程和参考文献[3-4]类似,在此省略.
3 定理1.1的证明
证明是建立在定理2.1的结果上,设u0,θ0∈C([0,+∞);H2)∩L2(0,+∞;H3)分别满足下面的线性抛物方程:
∂tu0-Δu0+p0=0,divu0=0,x∈Ω,
u0|∂Ω=0,u0|t=0=u0,∂tθ0-Δθ0=0,x∈Ω,

根据抛物方程的性质,得到:
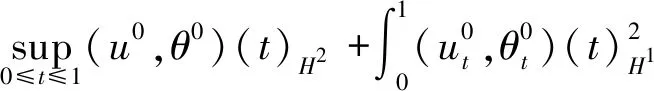


(3.2)
根据(3.1)和(3.2),如果(v,η)∶=(u0,θ0)满足定理(2.1)的假设,那么线性问题(2.1)在(0,T*)内也存在唯一的强解(ρ,u,p,θ)=(ρ1,u1,p1,θ1)且(v,η)=(u0,θ0),满足估计(2.14)-(2.17),若(v,η)=(u1,θ1)也满足定理(2.1)的假设,那么线性问题(2.1)在(0,T*)内存在唯一的强解(ρ,u,p,θ)=(ρ2,u2,p2,θ2)且(v,η)=(u1,θ1),满足估计(2.14)-(2.17).根据这种迭代过程,能够定义一个序列(ρi,ui,pi,θi),对任意的i≥1,(ρ,u,p,θ)=(ρi,ui,pi,θi)是线性问题(2.1)在(0,T*)内存在的唯一解,且(v,η)=(ui-1,θi-1)并且满足一致估计:

(3.3)


(3.4)
注:根据参考文献[3]易证明弱解(ρ,u,p,θ)关于时间的连续性和解的唯一性.在此省略.

