推摇组合式造波机参数研究与结构设计

张 楠,尹 阔,董志奎,姜文通,梅 林

(燕山大学 a.机械工程学院;b.电气工程学院,河北 秦皇岛 066004)

0 引 言

我国海域辽阔，海岸线长达1.5万km，管辖海域约300万km2，同时还有6 536个500 m2以上的岛屿，是一个名副其实的海洋大国。我国海洋事业依然面临严峻挑战，从海洋大国到海洋强国的征程任重而道远。我国长期“重陆轻海”，这种传统观念使我们严重缺乏对海洋的重视，充分利用海洋资源已经成为我们发展的迫切需要。

在海洋工程和港口与近海工程实验研究领域，由于地理因素以及海洋环境的复杂性与不确定性，户外实地实验往往具有一定的风险[1]。研究人员通常采用实验室水槽造波技术来模拟海洋波浪，波浪的模拟是一种重要的实验手段，而造波机是进行水槽实验的必备实验装置[2-3]。根据造波板运动形式的不同，可以分为平推式和摇摆式造波机。平推式造波机通过造波板沿水平方向的平推运动实现波浪的模拟；摇摆式造波机通过造波板绕底部铰链摇摆运动实现波浪的模拟[4-6]。平推式和摇摆式造波机由于造波原理不同，波形也各有特点，它们分别应用于不同的实验环境，由于实验要求的复杂性和多样性，在实验需要不同形式的波浪时，单一运动形式的造波机已不能满足要求，只能采取更换造波机的方法，提高了实验成本。

本文提出了一种推摇组合式造波机的新方案，根据秦皇岛近海海域7、8月份海浪浪高特点，对平推造波和摇摆造波两种工作模式的主要设计及工作性能参数进行理论分析与推导，并利用MATLAB 2016 M语言建立推导结果的数学模型，计算得到平推造波和摇摆造波两种工作模式的主要设计及工作性能参数。确定了推摇组合式造波机的设计方案，根据受力分析和仿真计算结果，验证了此方案的可行性。

1 造波实验水槽水深的确定

秦皇岛面朝渤海，属开放性海域，对北戴河老虎石外设立的波浪浮标站全年观测数据进行统计分析[7]，发现小于0.5 m的波浪出现频率为89.15%。其中7、8月份有效波高不超过0.5 m[8-9]，波浪的平均周期为1.6 s，最大周期为3.2 s[10]。

根据实际观测数据，确定了推摇组合式造波机造波能力最大波高为0.5 m。基于微幅波理论并根据破碎波高公式[11]和波浪的色散方程[12]讨论水深和周期的关系，破碎波高和波的色散方程如下：

式中：Hmax为最大波高；hmin为最小水深；k为波数，2π/λ=k;T为波浪周期，2π/T=ω。通过MATLAB中的M语言进行编程，建立了最小水深和周期的关系，如图1所示。

图1 最小水深与周期关系

从图1可以看到：随着水深的增加，波浪周期无限接近于1.5 s，这说明在最大波高0.5 m的条件下，当水深大于2.29 m时，即使进一步增大水深，也不能形成周期小于1.5 s的波浪。从实验室水槽建造的经济角度考虑，选择水槽的水深为1.03 m，在此条件下，可以制造出周期1.6～3.2 s，最大波高为0.5 m的波浪。

2 推摇组合式造波机参数

设坐标原点位于静水面与造波板初始位置的交点处，x轴与静水面重合，y轴垂直向上，d为造波板浸深，坐标示意图如图2所示。

图2 坐标示意图

在确定实验水槽水深为1.03 m后，分别讨论平推模式和摇摆模式不同周期条件下的行程与造波板浸深的关系，波高与行程比值如下[13]：

(3)

式中：

L0={sinh(k0h)+(σ-1)sinh[k0(h-d)]+

σ[cosh(k0h-k0d)-cosh(k0h)]/k0d}

H为波高;h为水深;d为浸深;k0为波数;S为造波机运动结构的行程，S=2Xa。当σ=0时，为平推造波模式;σ=1时，为摇摆造波模式。在波高和水深已知情况下，只有行程、浸深和周期未知，通过MATLAB M语言编程，建立了三者之间的关系。平推和摇摆造波模式下，行程和浸深的关系分别如图3、4所示。

图3 平推模式行程与浸深的关系图4 摇摆模式行程与浸深的关系

分析计算结果可知，在最大波高和水深不变的情况下，随着周期的减小，浸深的增大，造波机运动结构的行程相应减小。对于实验设备来说，行程越小则丝杠和导轨的价格越低，可有效节约实验设备加工和制造费用。基于此原则，在最大波高0.5 m前提下，选择周期1.6 s为对应于此波高的造波机设计周期。

由图3、4对比可知：同一周期和浸深条件下，摇摆模式的行程大于平推模式的行程，摇摆模式行程接近于平推模式行程的2倍。

平推与摇摆模式下，不同浸深条件，造波机运动结构最大运动速度与周期的关系计算结果分别如图5、6所示。在相同周期条件下，随着浸深的增大，造波机运动结构的最大运动速度v相应减小，从丝杠的实际最大安全运动速度的角度出发，并结合增大浸深亦可减小行程的计算结果，最终确定造波板浸深为1 m。

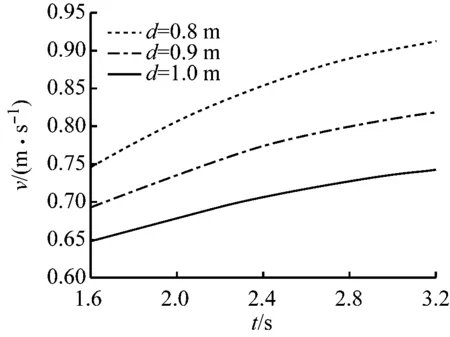
图5 平推模式速度与周期的关系图6 摇摆模式速度与周期的关系

由图5、6对比可知：同一浸深和周期条件下，摇摆模式的速度大于平推模式的速度，摇摆模式的速度接近于平推模式速度的两倍。

在确定推摇组合式造波机最大造波波浪高度0.5 m(设计波高)、造波实验水槽水深、造波机设计周期及造波板浸深，并相应确定推摇组合式造波机运动结构的最大行程和最大速度后，根据式(3)计算出本实验设备推摇组合式造波机造波波高能力曲线图，如图7所示。由图7可知，本实验设备能造出周期1.6～3.2 s，对应波高0.5～0.22 m(平推模式)，0.5～0.19 m(摇摆模式)的波浪。

图7 造波能力曲线

3 推摇组合式造波机结构设计与作用力分析

3.1 推摇组合式造波机结构设计

根据造波板浸深和最大波高，确定造波板净高度为1.28 m，并进一步根据推摇组合式造波机运动结构的行程及工作特点，设计推摇组合式造波机机械结构如图8所示。

造波机结构材料采用45号钢，造波板质量207 kg，造波架质量122 kg。即平推模式下，造波机运动结构质量为329 kg；摇摆模式下，造波机运动结构质量为207 kg。

3.2 推摇组合式造波机作用力分析

根据微幅波理论和伯努利方程[12]，推导得到造波板的压力场公式：

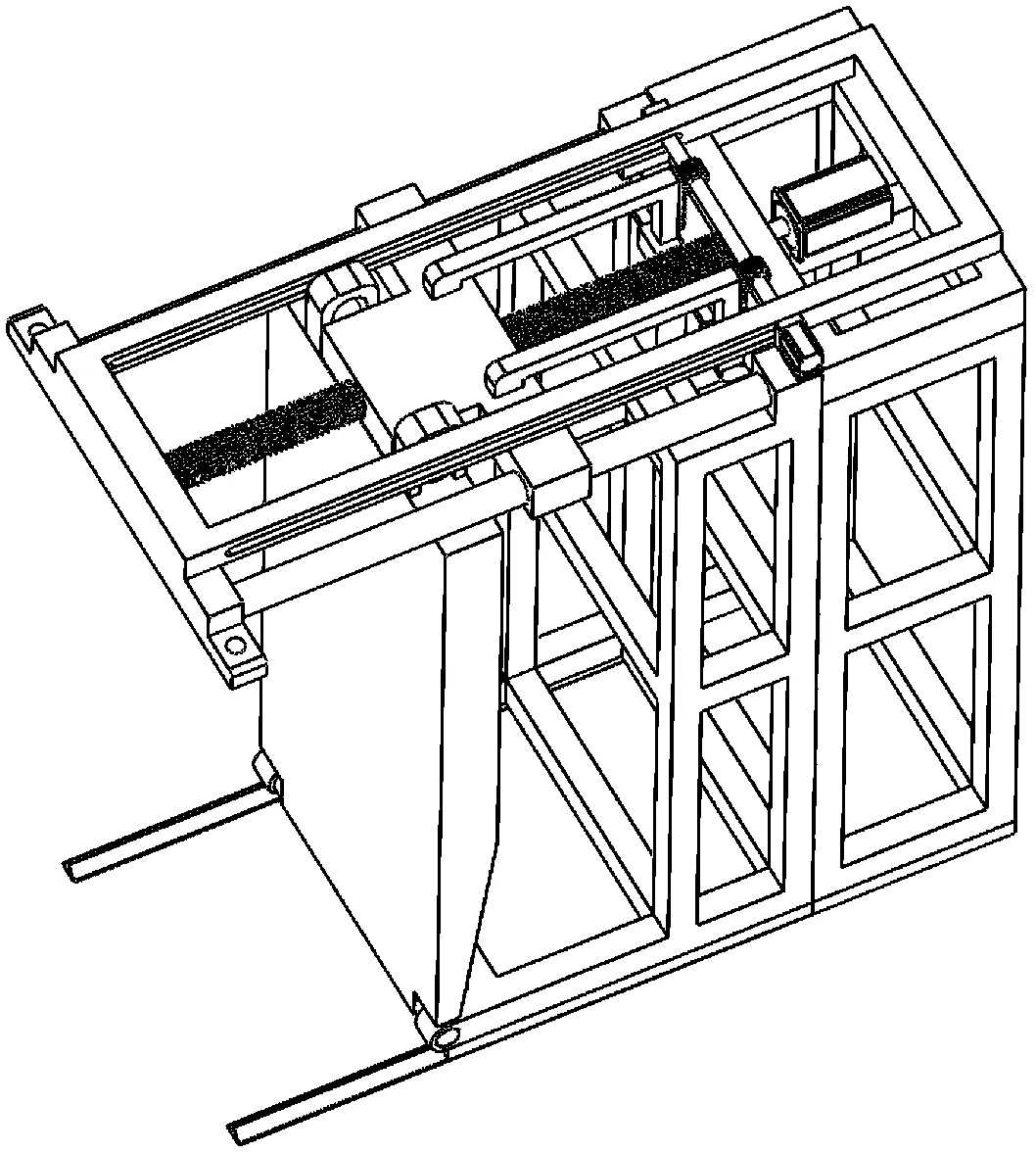
图8 推摇组合式造波机机械结构示意图

(4)

速度势φ(x,y,t)函数为：

φ(x,y,t)=cosωt·C0cosh[k0(y+h)]sink0x+

(5)

(6)

(7)

式中：

Ln=sin(knh)+(σ-1)sin[kn(h-d)]+

σ[cos(knh)-cos(knh-knd)]/(knd)

造波板在运动过程中会受到规则波力、扰动驻波力以及造波板惯性力的作用，已知推出的速度势φ(x,y,t)函数中包括规则波和扰动驻波两部分，分别对规则波和扰动驻波沿造波板面板积分得到平推模式的规则波力和扰动驻波力。

平推模式规则波力：

sinh[k0(h-d)]}/k0

(8)

(9)

平推模式扰动驻波力：

sin[kn(h-d)]}/kn

(10)

(11)

式中：B为造波板宽度，本设计方案造波板宽度为0.6 m;kn通过ω2=-gkntan(knh)求得[14]。

摇摆模式造波过程中[15]，不同水深对造波板底部铰链存在一个力臂(y+d)，电动缸对造波板底部铰链也存在一个力臂(d1+d)，d1为电动缸与坐标原点的垂直距离，本案例d1=0.3 m，因而推导出的摇摆模式规则波力和扰动驻波力如下：

摇摆模式规则波力：

(12)

C3=[k0dsinh(k0h)+cosh(k0h-k0d)-

cosh(k0h)]2

(13)

摇摆模式扰动驻波力：

(14)

C4=[kndsin(knh)-cos(knh-knd)+

cos(knh)]2

(15)

造波板惯性力通过下式求得:

(16)

式中：y1为造波板质心相对于坐标系原点的位置，本案例y1=-0.293 m；m为造波机运动结构质量。

电动缸作用于造波板的总力：

F=F0cosωt+Fnsinωt+Fasinωt

(17)

最大单元负载力：

(18)

电动缸功率：

(19)

将推出的作用力公式通过MATLAB M语言进行编程，计算结果如图9～11所示。

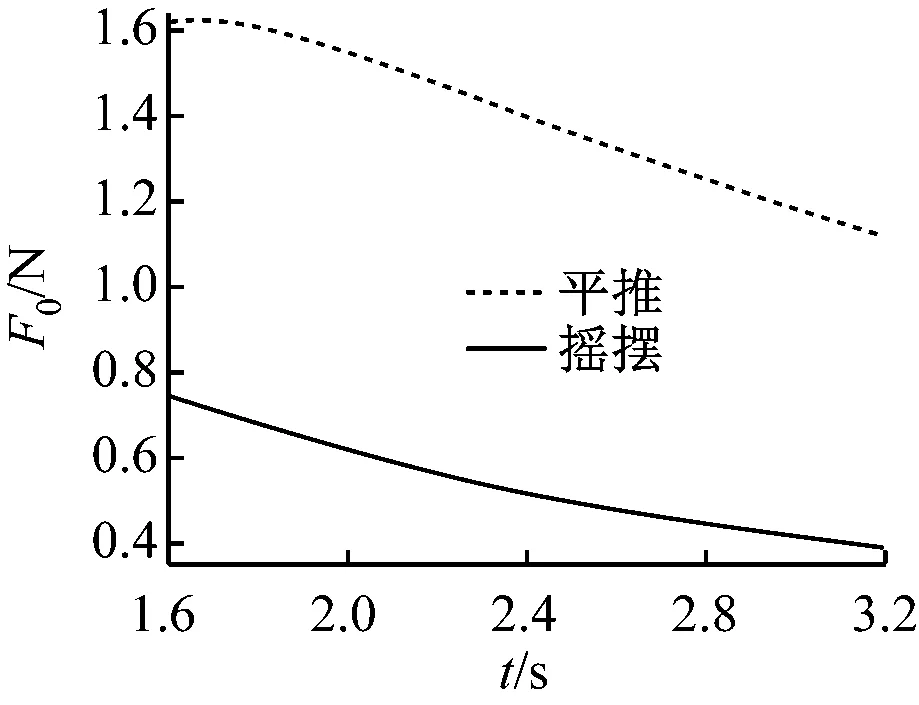
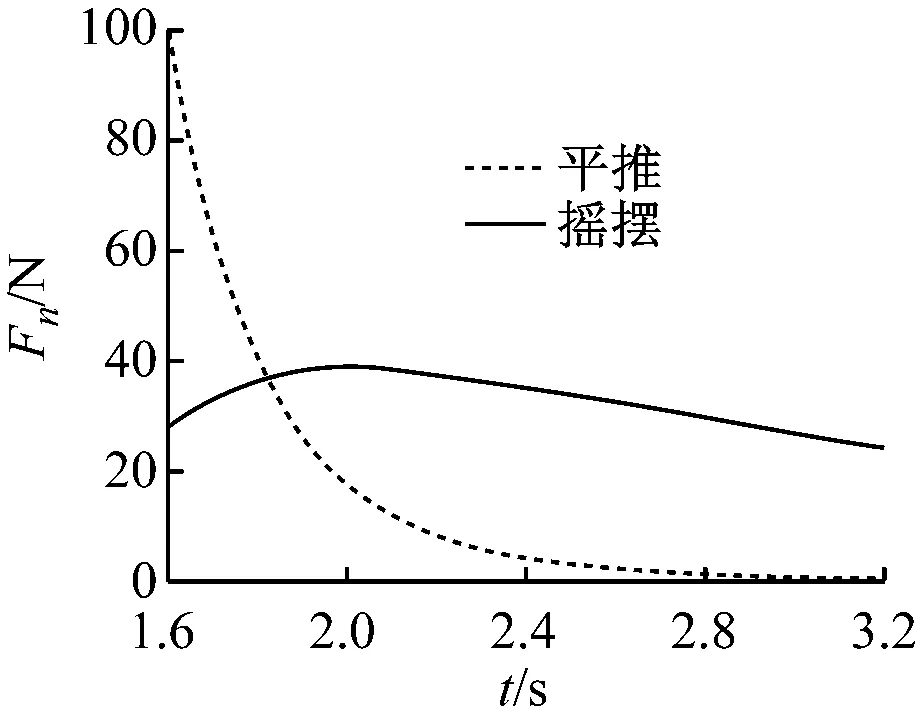
图9 平推和摇摆规则波力图10 平推和摇摆扰动驻波力

图11 平推和摇摆惯性力

通过分析计算结果可知：同一波高、周期条件下，平推模式的规则波力大于摇摆模式的规则波力，平推模式的规则波力接近于摇摆模式规则波力的2倍；平推模式的扰动驻波力随着周期增大，逐渐趋于零，摇摆模式的扰动驻波力在给定周期范围内则相对变化不大，比较稳定；平推模式的惯性力大于摇摆模式的惯性力。

通过以上推导与计算，最终确定推摇组合式造波机的主要参数(设计周期条件下)如表1所示。

表1 推摇组合式造波机主要参数

3.3 推摇组合式造波机受力分析

由式(4)可知，造波板所受到的力是随时间和空间变化的，因此采用ANSYS中的瞬态动力学分析模块对其受力作仿真分析，将推导出的压力场公式以Function函数的形式导入到ANSYS中，对应力和总变形进行求解,得到图12～15结果。

图12 平推模式总应力云图图13 平推模式总变形云图

图14 摇摆模式总应力云图图15 摇摆模式总变形云图

工作过程中，造波机机械结构的最大变形为2.3 mm，最大应力为62.432 MPa，最大变形在本造波机机械运动最大允许误差范围内，最大应力远小于材料屈服极限335 MPa，从瞬态动力学分析的角度，认为本设计方案是可行的。

4 结 语

根据实验造波需要，本文针对秦皇岛近海海域7、8月份海浪特点，依据微幅波理论，研究了在波高一定的情况下造波实验水槽水深与周期的关系，平推造波和摇摆造波两种工作模式的主要设计及工作性能参数。利用MATLAB 2016 M语言建立平推造波和摇摆造波主要设计及工作性能参数的数学模型，计算出两种工作模式下推摇组合式造波机运动结构的周期、浸深与行程，浸深、周期与速度，作用力与周期等的关系，得到了平推造波和摇摆造波两种工作模式下的主要设计及工作性能参数。在此基础上设计推摇组合式造波机机械结构，并对其做受力及瞬态动力学分析，仿真结果验证了本设计方案的可行性，为加工制造推摇组合式造波机和开展实验造波工作提供了重要理论基础及设计依据。