基坑开挖引起复合地基下方既有双线地铁隧道位移的计算方法
卜康正, 郑先昌, 张万照, 郭劲睿, 沈 翔
(1. 广州大学土木工程学院, 广东 广州 510006; 2. 中铁南方投资集团有限公司, 广东 深圳 518052)
0 引言
随着我国地铁隧道的不断建设,沿线地区工程日益增多,尤其是地铁隧道上方的基坑开挖工程。基坑开挖卸荷造成的土体变形必然会带动下卧隧道产生位移,而位移过大则会破坏隧道结构、影响地铁的正常运营。根据暂行办法[1]规定: 隧道结构绝对沉降量及水平位移量须≤20 mm(包括各种加载和卸载的最终位移量)。对此,人们常采用地基加固形成桩-土复合地基的方法减少隧道的位移。因此,如何合理地预测基坑开挖引起复合地基下方既有隧道的位移是当前急需解决的一个工程难题。
目前,国内外学者针对基坑开挖引起下方既有隧道位移这一工程问题做了很多研究。在数值模拟方面,黄宏伟等[2]通过PLAXIS有限元软件分析了上海外滩通道基坑开挖对下方既有延安东路隧道竖向位移的影响,并对地基加固措施效果进行评价; 王定军等[3]利用FLAC3D有限元软件研究了深圳市桂庙路改造工程基坑开挖对下方隧道结构竖向位移和受力的影响,并针对该工程提出复合地基加固宽度和深度的合理取值; 赵俊等[4]结合南京南站北广场地下空间开发工程,利用FLAC3D有限元软件分析了坑底复合地基模量比的改变对下方隧道竖向位移的影响。数值模拟方法往往采用大型有限元软件,建模工作量较大,且一般只能针对某个具体工程展开研究。因此,针对类似工程问题,提出简化、高效的理论计算方法是十分必要的。
现有理论计算主要采用2阶段分析方法[5-10],即第1阶段基于Mindlin应力解,推导出作用在隧道上的竖向附加荷载; 第2阶段通过Winkler地基梁模型和Galerkin法,计算得到隧道的竖向位移。该方法考虑了坑底与坑壁荷载、基坑围护结构和基坑降水对隧道竖向位移的影响,但是,没有计算出隧道的横向位移,也未考虑坑底地基加固对隧道位移的影响,而且第1阶段计算方法还可继续优化,计算效率也可进一步提高。
地铁隧道往往是双线建设的,对此,有学者提出双线隧道存在“双洞效应”,并在原有计算单线隧道竖向位移的理论基础上,通过一次性法计算得到竖向“双洞效应”引起隧道的竖向位移[11]。但是,没有考虑双线隧道横向“双洞效应”的影响,且一次性计算得到“双洞效应”引起隧道位移的方法不够严谨。
针对以上不足,本文在原有2阶段分析方法的基础上做了以下创新: 1)第1阶段基于Mindlin位移解[12],引入Winkler地基模型,反推出复合地基下方既有单线隧道的竖向和横向附加荷载; 2)第2阶段通过文献[5]的方法以及迭代法,计算得到复合地基下方既有双线隧道轴线上任意一点的竖向和横向位移。以期为类似基坑工程的设计与施工以及基坑下方既有隧道灾害的防治提供更高效、合理的理论计算依据。
1 利用Mindlin理论推导隧道竖向位移
1.1 基坑开挖引起的竖向位移公式
如图1所示,设基坑的纵向长为a,横向宽为b,深度为h,隧道位置与地面距离为z。
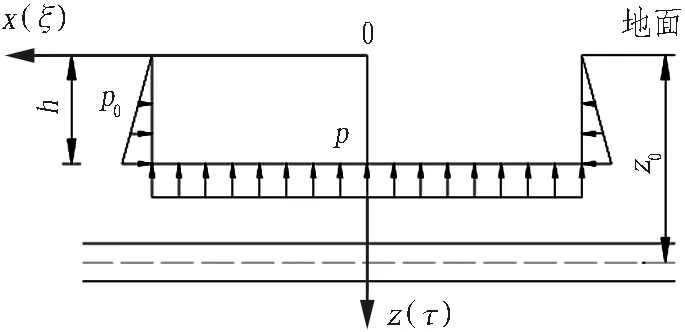
(a) 纵向剖面图

(b) 横向剖面图

(c) 俯视图
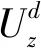
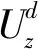
(1)
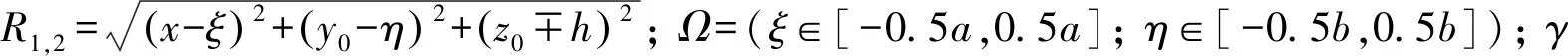
根据文献[11],受到基坑围护结构的影响,基坑侧壁Cn面上的水平荷载为p0=K0γτ-Q1(其中Q1为主动土压力)。水平荷载引起下方土层中的点(x,y0,z0)竖向位移为

(2)
式中:z3=z0-τ;z4=z0+τ;ν3=1-2ν;βn=(η,ξ,η,ξ);Xn=(x-0.5a,y0+0.5b,x+0.5a,y0-0.5b); Πn,1=((η∈[-0.5b,0.5b],τ∈[0,h]),(ξ∈[-0.5a,0.5a],τ∈[0,h]),(η∈[-0.5b,0.5b],τ∈[0,h]),(ξ∈[-0.5a,0.5a],τ∈[0,h]));
由文献[11]可知,本文算例分析中的人工填土属于黏性土。
此外,围护结构会嵌入坑底一定深度,受到围护结构嵌入坑底部分“遮拦效应”[13]的影响,侧壁卸载无法直接引起坑底下方土体产生位移。“遮拦效应”是通过围护结构嵌入坑底部分的侧摩阻力来实现的,因此,“遮拦效应”抵消的土体竖向位移
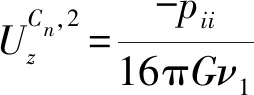
(3)
式中:zc1=zc-τ;zc2=zc+τ; Πn,2=((η∈[-0.5b,0.5b],τ∈[0,hc]), (ξ∈[-0.5a,0.5a],τ∈[0,hc]), (η∈[-0.5b,0.5b],τ∈[0,hc]), (ξ∈[-0.5a,0.5a],τ∈[0,hc]));
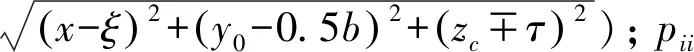
若嵌入的土层共有w1层,则在坑底和坑壁荷载的作用下,基坑下方土层中任意一点(x,y0,z0)的竖向位移为
(4)
1.2 复合地基侧摩阻力引起的竖向位移公式
当基坑开挖卸荷后,基坑底部桩-土复合地基受力,将部分卸载应力传递给下卧层中,另一部分通过桩土接触面上的侧摩阻力传递给桩。对于通过接触侧面传递给桩的荷载,可以看成由侧摩阻力组成的竖直向下的面荷载。当桩径不大时,可以忽略弯矩的影响,把面荷载等效成作用点在桩中心的线荷载,以单桩为例,如图2所示。
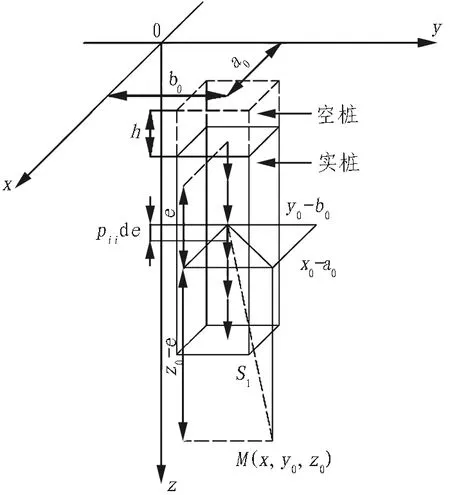
图2 单桩Fm侧摩阻力引起的竖向位移
Fig. 2 Vertical displacement caused by lateral resistance of
single pileFm
第ii个加固土层中中心坐标为(a0,b0,τ)的单桩Fm,其实桩侧摩阻力引起下方土层中的点(x,y0,z0)竖向位移为
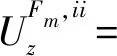
(5)

若加固土层共有w1层,且有w2个桩,则在侧摩阻力的作用下,基坑下方土层中任意一点(x,y0,z0)产生的竖向位移为
(6)
由叠加原理可得,基坑下方土层中任意一点(x,y0,z0)产生的总竖向位移为
(7)
1.3 隧道刚度的影响
由于隧道刚度较大,不考虑隧道刚度计算出的隧道轴线上土体竖向位移实际上远大于隧道在轴线上的竖向位移。因此,本文引入Winkler地基模型,先推导出在地铁隧道轴线上任意一点(x,y0,z0)产生的总竖向荷载公式
(8)
式中:Kz为土弹簧刚度,Kz=kz·D(其中D为隧道外直径;kz为地基竖向基床系数)。
采用Vesic公式
(9)
式中EI为盾构隧道纵向弯曲刚度。
然后,考虑隧道刚度的影响,即把由螺栓和管片拼装的盾构隧道等效成相同刚度的均匀、连续的无限长梁,并且下卧地基土上,隧道与周边土体位移协调。由于总竖向附加荷载的值不变,因此,由文献[5]可得
(10)
式中Uz为隧道轴线上点(x,y0,z0)的竖向位移。
最后,根据文献5,运用一维三次二节点单元的形函数(hermite型)和Galerkin法,通过matlab编程求出隧道轴线上各单元节点的竖向位移Uz。
2 双线隧道的竖向“双洞效应”
双线临近隧道1、隧道2之间存在着竖向“双洞效应”,则根据Mindlin位移解,通过积分的方法,推导出临近隧道2对土体的竖向附加接触压力Fz21(x)引起隧道1点(x,y0,z0)上土体的竖向位移为
(11)

(12)


3 利用Mindlin理论推导隧道横向位移
3.1 基坑开挖引起的横向位移公式
基坑底面均布荷载p引起下方土层中的点(x,y0,z0)横向位移为
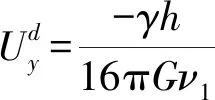
(13)
基坑侧壁C1、C3面水平荷载p0引起下方土层中的点(x,y0,z0)横向位移为

(14)
式中Xn=∓x-0.5a。
基坑侧壁C2、C4面水平荷载p0引起下方土层中的点(x,y0,z0)横向位移为
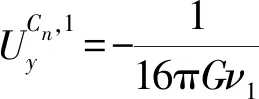
(15)
式中Xn=y0±0.5b。
侧壁卸载时,“遮拦效应”抵消的土体横向位移为


(16)
式中Yn=(y0-η,y0+0.5b,y0-η,y0-0.5b)。
若嵌入的土层共有w1层,则在坑底和坑壁荷载的作用下,基坑下方土层中任意一点(x,y0,z0)产生的横向位移为
(17)
3.2 复合地基侧摩阻力引起的横向位移公式
第ii个加固土层单桩Fm的侧摩阻力引起基坑下方土层中的点(x,y0,z0)横向位移为
(18)
若加固土层共有w1层,且有w2个桩,则在侧摩阻力的作用下,基坑下方土层中任意一点(x,y0,z0)产生的横向位移
(19)
由叠加原理可得,基坑下方土层中任意一点(x,y0,z0)产生的总横向位移为
(20)
结合1.3节的方法,可以得到不考虑横向“双洞效应”情况下,隧道轴线上各单元节点的横向位移Uy。
3.3 横向“双洞效应”引起的隧道横向位移公式
临近隧道2对土体的横向附加接触压力Fy21引起隧道1点(x,y0,z0)上的土体横向位移为
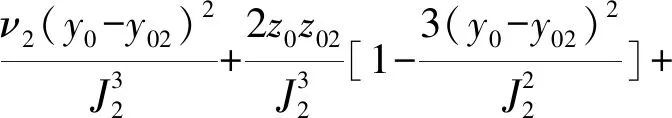
(21)
结合第2节和地基水平基床系数ky,可以得到考虑横向“双洞效应”的情况下,地铁隧道1任意一点(x,y0,z0)的横向位移Uy3。根据文献[17]中的图7,采用线性内插法或者外伸法得到水平基床系数的比例系数α,可得地基水平基床系数
ky=α·Es[17]。
(22)
同理,可以计算出考虑横向“双洞效应”的情况下,地铁隧道2轴线上任意一点(x,y0,z0)的横向位移。
4 算例分析
为了验证本文计算的合理性,依托深圳地铁5号线湖滨西路市政工程2标段的基坑开挖实例进行对比分析。该基坑a为65 m,b为38.5 m,h为8.6 m,坑壁围护结构嵌入坑底深度为3 m,坑底加固采用φ180 mm@1.5 m的树根桩(方桩),且桩以基坑2条中轴线为基准对称布置,树根桩(实桩部分)在坑底各加固土层的极限侧摩阻力标准值以及土层加固前的物理力学参数分别如表1和表2所示。

表1 加固土层参数
双线隧道轴线处埋深均为16.1 m,左线隧道轴线在基坑纵向中轴线左侧7 m处,右线隧道轴线在基坑纵向中轴线右侧8 m处,每环隧道管片D为6 m,EI为3.55×107kN/m。隧道所在土层kz为5.3×103kN/m2。水平基床系数的比例系数α取值为0.5,因此ky取值为4×103kN/m2。

表2 土层加固前的物理力学参数
通过本文计算方法与实测数据、文献[5]和文献[9]的计算方法(基于Mindlin应力解,分别采用Winkler和Pasternak地基梁模型计算得到隧道位移均没考虑侧摩阻力和“双洞效应”的影响)进行对比,得到曲线如图3所示。竖向位移以隧道隆起为正,横向位移以隧道向基坑内侧位移为正(下同)。
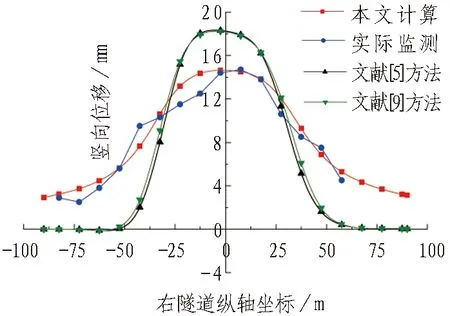
(a) 右隧道竖向位移
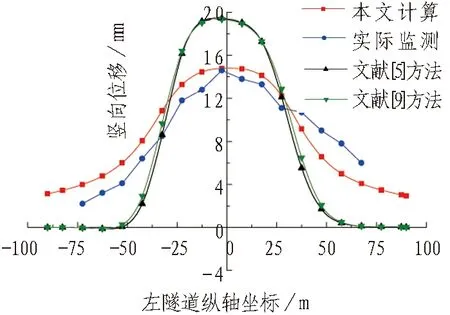
(b) 左隧道竖向位移
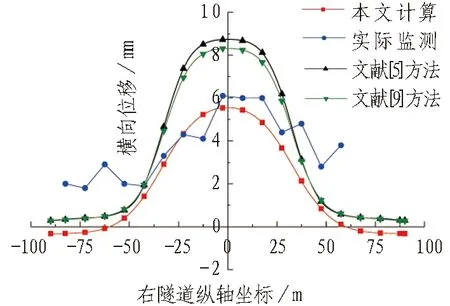
(c) 右隧道横向位移

(d) 左隧道横向位移
由图3可知,本文的理论计算位移量相比于文献[5]和文献[9]方法,与实测数据更为吻合。这是由于本文计算不仅考虑侧摩阻力和双洞效应的影响,而且采用的Mindlin位移解公式比Mindlin应力解公式多了1个参数(剪切弹性模量),因此,本文计算结果更加可靠、合理。
利用matlab 2014b在笔记本电脑华硕X450V上编程,将运算本文理论计算方法的时间与运算原2阶段分析方法的时间作对比,结果如表3所示。
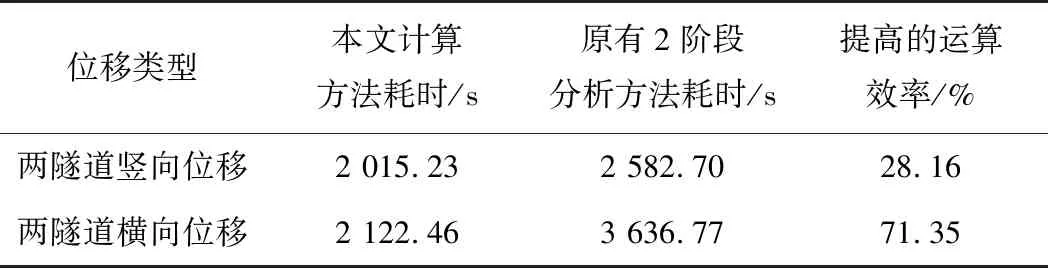
表3 运算时间对比结果
由表3可知,本文理论计算能提高原有2阶段分析方法的运算效率28%以上。
对算例中隧道位移的影响因素进行分析,结果如图4所示。

(a) 隧道竖向位移
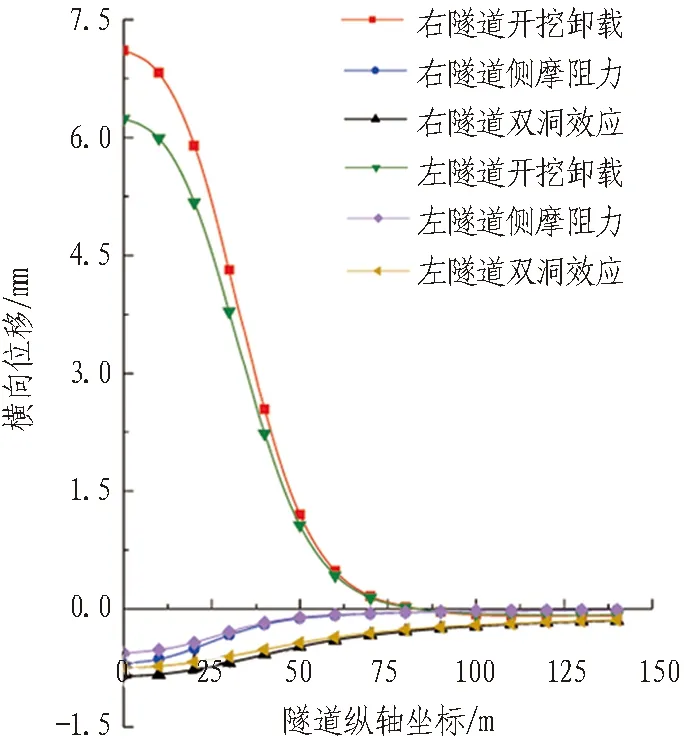
(b) 隧道横向位移
Fig. 4 Analysis of influencing factors of tunnel displacement in practical calculation example
由图4可知: 1)隧道产生位移的主要原因是基坑开挖卸载。2)侧摩阻力在[0 m, 50 m]区间对隧道位移影响较大,表现为减少隧道正向位移,最大值在基坑中点处。隧道隆起减少量最大值为-2.12 mm,约为该点总隆起量的14.4%;隧道横向位移减少量最大值为 -0.70 mm,约为该点总横向位移量的12.6%。因此,侧摩阻力对隧道位移的影响是不可忽略的。3)“双洞效应”减少隧道正向位移,对隧道隆起量影响较小,但对隧道横向位移影响较大,最大值在基坑中点处。隧道隆起减少量最大值为-0.44 mm,约是该点总隆起量的3.0%;横向位移减少量最大值为-0.86 mm,约是该点总横向位移量的15.4%。因此,“双洞效应”对隧道位移的影响也是不可忽略的。
4.1 桩参数改变对侧摩阻力引起隧道位移的影响分析
4.1.1 桩长改变的影响
改变算例中坑底加固土体厚度,即实桩桩长依次取1.5、 2、 2.5、 3、 3.5 m,各加固土层厚度按照原厚度比例变化,得到侧摩阻力引起左隧道位移的计算结果如图5所示。本文选择离基坑中轴线更近的左隧道进行研究,下同。

(a) 左隧道隆起减少量

(b) 左隧道横向位移减少量
Fig. 5 Influence of pile length on tunnel displacement caused by lateral resistance
由图5可知,桩长改变对侧摩阻力引起隧道位移的影响较大。1)随着桩长的增大,隧道隆起减少量均匀增长,但横向位移减少量的增长幅度越来越小,且在桩长大于3 m之后,曲线逐渐趋于恒定; 2)侧摩阻力对隧道位移的影响范围始终不变,约为3.2倍基坑纵向长度,且减少量最大值均在基坑中点处。
4.1.2 桩距改变的影响
分别改变算例中桩的纵向距离或横向距离,两者依次取0.5、 1、 1.5、 2、 2.5、 3 m,且桩仍以基坑2条中轴线为基准对称布置,得到侧摩阻力引起左隧道位移的计算结果如图6和图7所示。

(a) 左隧道隆起减少量

(b) 左隧道横向位移减少量
Fig. 6 Influence of pile longitudinal distance on tunnel displacement caused by lateral resistance
由图6和图7可知,桩纵向距离或横向距离改变对侧摩阻力引起隧道位移的影响较大。1)随着桩纵向距离或横向距离的减小,隧道位移减少量的增大幅度越来越大; 2)侧摩阻力对隧道位移的影响范围始终不变,且减少量最大值均在基坑中点处。

(a) 左隧道隆起减少量

(b) 左隧道横向位移减少量
Fig. 7 Influence of pile lateral distance on tunnel displacement caused by lateral resistance
4.2 隧道位置改变对侧摩阻力引起隧道位移的影响分析
4.2.1 隧道竖向位置改变的影响
改变算例中左隧道的竖向位置,使它的轴线依次在复合地基下方3、 4.5、 6、 7.5、 9、 10.5、 12、 13.5 m处,并对黏土层厚度作相应的调整,使隧道始终处于黏土层中,得到侧摩阻力引起左隧道位移的计算结果如图8所示。
由图8可知,隧道竖向位置改变对侧摩阻力引起隧道隆起的影响较小,对横向位移的影响较大。1)在[0 m, 25 m]区间内,随着与复合地基竖向距离的增大,隧道隆起减少量均匀减小,但减小幅度不大。其余区间的隧道隆起减少量几乎不变。2)随着与复合地基竖向距离的增大,隧道横向位移减少量不断增大,但增大幅度越来越小,且在竖向距离大于10.5 m之后,横向位移减少量曲线逐渐趋于恒定。3)侧摩阻力对隧道位移的影响范围始终不变,且减少量最大值均在基坑中点处。
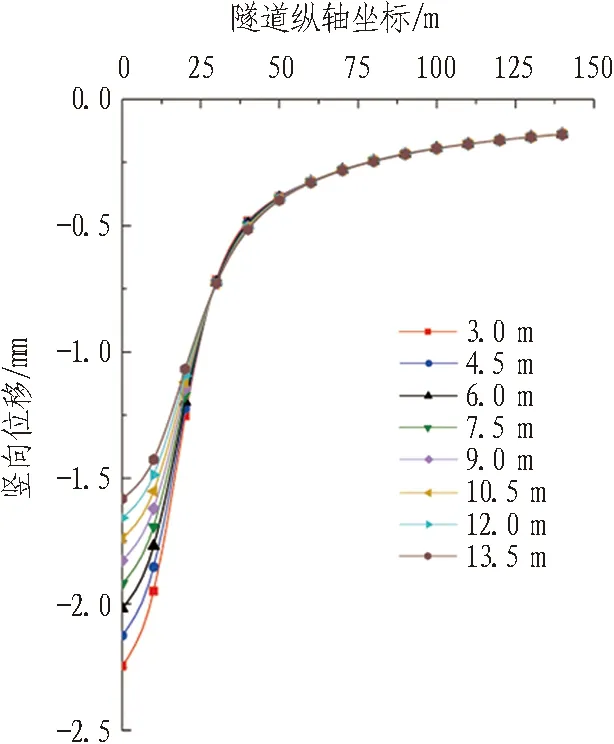
(a) 左隧道隆起减少量
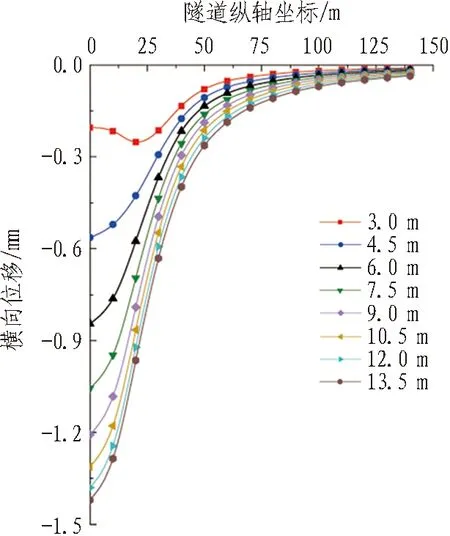
(b) 左隧道横向位移减少量
Fig. 8 Influence of tunnel vertical position on tunnel displacement caused by lateral resistance
4.2.2 隧道横向位置改变的影响
改变算例中左隧道的横向位置,使它的轴线与基坑中轴线横向距离依次为0.5、3.5、6.5、9.5、12.5、15.5、18.5 m,得到侧摩阻力引起左隧道位移的计算结果如图9所示。
由图9可知,隧道横向位置改变对侧摩阻力引起隧道位移的影响较大。1)在[0 m,25 m]区间内,随着与基坑中轴线横向距离的减小,隧道隆起减少量均匀增大,但在横向距离小于3.5 m之后,隆起减少量曲线逐渐趋于恒定。其余区间的隧道隆起减少量几乎不变。2)随着与基坑中轴线横向距离的增大,横向位移减少量均匀增大,且增大幅度较大,但在横向距离大于12.5 m之后,横向位移减少量曲线逐渐趋于恒定。3)侧摩阻力对隧道位移的影响范围始终不变,且减少量最大值均在基坑中点处。
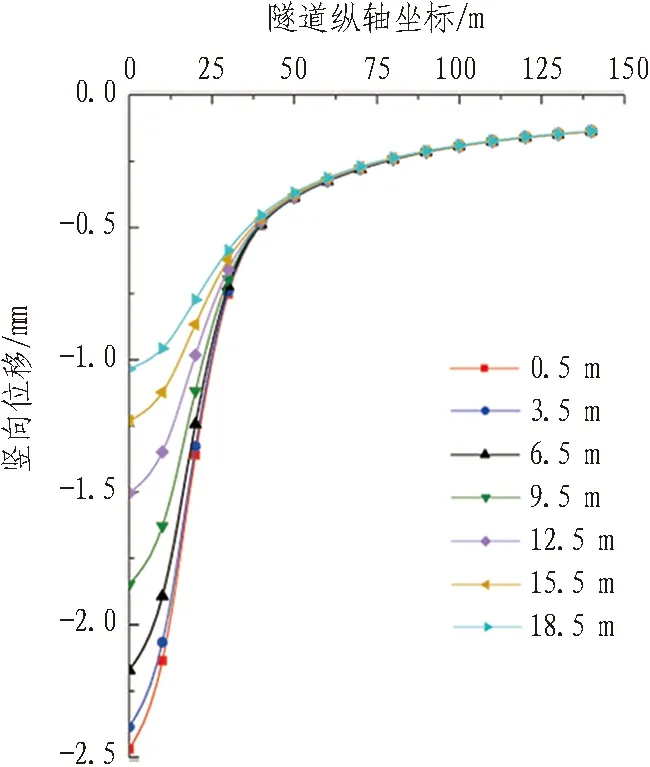
(a) 左隧道隆起减少量 (b) 左隧道横向位移减少量
图9隧道横向位置改变对侧摩阻力引起隧道位移的影响
Fig. 9 Influence of tunnel lateral position on tunnel displacement caused by lateral resistance
4.3 隧道位置改变对“双洞效应”引起隧道位移的影响分析
4.3.1 隧道竖向相对位置改变的影响
改变算例中左隧道的竖向位置,使它的轴线与右隧道轴线竖向距离依次为-1.5、0、1.5、3、4.5、6、7.5、9 m,正值表示在右隧道下方,得到“双洞效应”引起左隧道位移的计算结果如图10(a)、(b)所示。以“(迭代法计算结果-一次性法计算结果)/迭代法计算结果”作为一次性法的计算误差,误差计算结果如图10(c)、(d)所示,下同。

(a) 左隧道隆起减少量

(b) 左隧道横向位移减少量
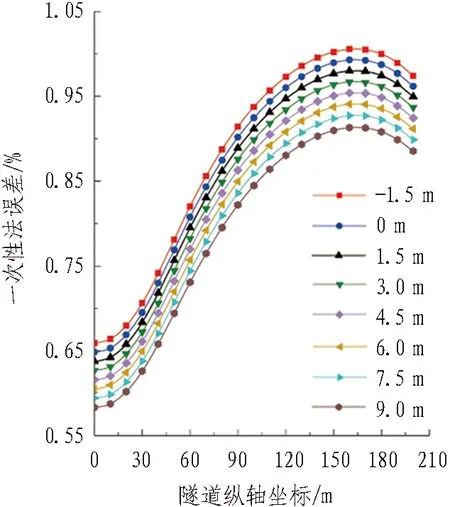
(c) 竖向“双洞效应”计算误差
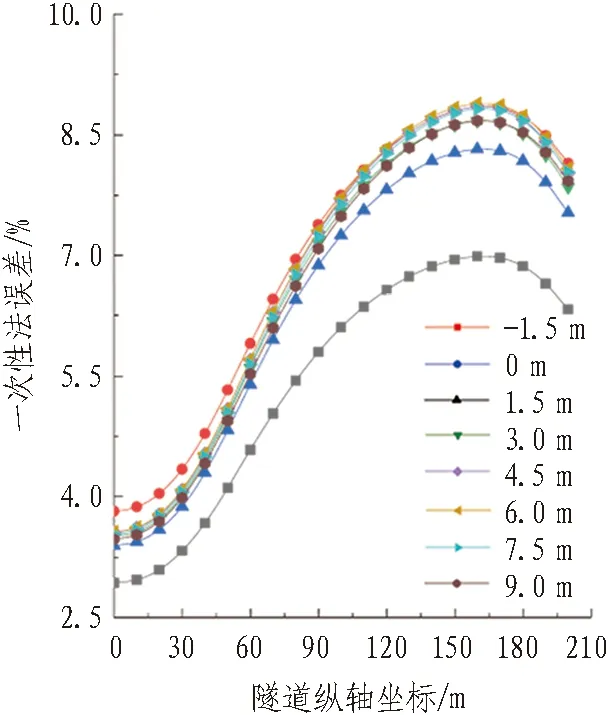
(d) 横向“双洞效应”计算误差
图10隧道竖向相对位置改变对“双洞效应”引起隧道位移的影响
Fig. 10 Influence of vertical relative position of tunnel on tunnel displacement caused by "double-tube effect"
由图10(a)、(b)可知: 1)隧道竖向相对位置改变对竖向“双洞效应”引起隧道竖向位移影响较小。左隧道隆起减少量最大值都在基坑中点,且都在[-0.45 mm,-0.4 mm]范围; 而左隧道横向位移减少量随着两隧道竖向距离的增大,先减小后增大,但最大值都在基坑中点,且除了竖向距离为0 m时最大值达到-0.75 m外,其余最大值都在[-0.5 mm,-0.7 mm]范围。2)“双洞效应”对隧道位移的影响范围始终不变,约为3.2倍基坑纵向长度。
由图10(c)、(d)可知: 1)随着竖向距离的增大,一次性法计算竖向“双洞效应”引起隧道竖向位移的误差均匀减小,最大误差数值小于1.05%。2)随着两隧道竖向距离的增大,一次性法计算横向“双洞效应”引起隧道横向位移的误差先增大后减小,但在竖向距离大于3 m之后,横向“双洞效应”误差曲线逐渐趋于恒定。最大误差数值较大,达到8.9%。
4.3.2 隧道横向相对位置改变的影响
改变算例中左隧道的横向位置,使它的轴线与右隧道轴线横向距离依次为8.5、 11.5、 14.5、 17.5、 20.5、 23.5、 26.5 m,得到“双洞效应”引起左隧道位移的计算结果如图11所示。

(a) 左隧道隆起减少量

(b) 左隧道横向位移减少量

(c) 竖向“双洞效应”计算误差
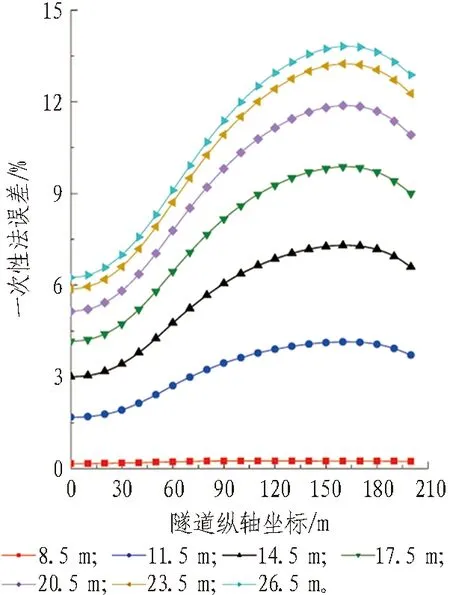
(d) 横向“双洞效应”计算误差
图11隧道横向相对位置改变对“双洞效应”引起隧道位移的影响
Fig. 11 Influence of lateral relative position of tunnel on tunnel displacement caused by "double-tube effect"
由图11(a)、(b)可知: 1)隧道横向相对位置改变对“双洞效应”引起隧道位移影响较大。随着两隧道横向距离的增大,左隧道隆起减少量均匀减小。而左隧道横向位移减少量则在[-0 m,50 m]区间缓慢减小,其余区间几乎不变。2)“双洞效应”对隧道位移的影响范围始终不变。
由图11(c)、(d)可知: 1)随着两隧道横向距离的增大,一次性法计算竖向“双洞效应”引起隧道竖向位移的误差均匀减小,最大误差数值小于1.15%。2)随着两隧道横向距离的增大,一次性法计算横向“双洞效应”引起隧道横向位移的误差不断增大,但增大幅度越来越小。在横向距离大于23.5 m之后,横向“双洞效应”误差曲线逐渐趋于恒定,最大误差数值较大,达到13.8%。
综合图10(c)、(d)和图11(c)、(d)可知,当计算竖向“双洞效应”引起隧道竖向位移,且不需要更精确严谨的理论计算结果时,可以选用一次性法计算;但当计算横向“双洞效应”引起隧道横向位移时,特别是当两隧道距离不过于接近(两隧道轴线竖向距离不小于3 m或横向距离不小于14.5 m)时,由于一次性法计算误差过大,必须选用迭代法计算。
5 结论与建议
1)本文基于Mindlin位移解公式推导并计算得到基坑开挖所引起下方既有双线地铁隧道的位移。由于Mindlin位移解公式复杂程度不到Mindlin应力解公式的一半,且多了1个参数,因此,本文计算方法运算效率更高、更合理。此外,本文计算还考虑了复合地基和隧道“双洞效应”的影响,因此,计算结果与实际工程更为吻合,可以对复合地基下方既有双线地铁隧道的安全进行评估,具有实用价值。
2)由实际算例分析可知,复合地基中桩的侧摩阻力和“双洞效应”对隧道位移的影响表现为减小基坑开挖引起的隧道隆起和横向位移,且影响范围始终不变,约为3.2倍基坑纵向长度;侧摩阻力和“双洞效应”引起隧道位移的最大值,分别约占该点总隧道位移的14.4%和15.4%,证明侧摩阻力和“双洞效应”对隧道位移的影响是不可忽略的。
3)当桩长、两隧道之间距离增大到某个合理的取值之后,侧摩阻力或横向“双洞效应”引起隧道横向位移趋于恒定。因此,为了经济且有效地减少隧道横向位移,坑底加固桩桩长和预先设计的两隧道之间距离应该合理选取,不宜过大;两隧道之间距离的大小都与侧摩阻力或竖向“双洞效应”引起隧道竖向位移大小成反比。因此,为了有效地减少隧道竖向位移,在施工条件和规范允许情况下,应尽量减少预先设计的两隧道之间距离。
4)迭代法比一次性法更加合理精确。特别是当计算横向“双洞效应”引起隧道横向位移时,由于在大部分情况下采用一次性法计算的误差过大,因此,应尽量采用迭代法计算。
5)本文计算做了较多简化,如未考虑分层分块开挖、降水等对隧道位移的影响,因此,理论计算结果仍存在一定误差,今后可在本文计算方法基础上做进一步研究。

