基于优化FAHP-TOPSIS法的高压富水花岗岩断层涌水预测

袁 青, 陈培帅, 钟 涵, 江 鸿, 吴诗琦, 闫鑫雨

(1. 中交第二航务工程局有限公司， 湖北 武汉 430040； 2. 中国地质大学(武汉)工程学院， 湖北 武汉 430074； 3. 交通运输行业交通基础设施智能制造技术研发中心， 湖北 武汉 430040； 4. 长大桥梁建设施工技术交通行业重点实验室， 湖北 武汉 430040)

0 引言

隧道穿越花岗岩断层带最主要的施工灾害就是高压富水体的涌突，其危险性极高，破坏力巨大，严重影响隧道施工安全，如何准确预测隧道涌水灾害的涌水等级及涌水量有着重要意义。目前，理论计算方法有地下水动力学[1]、地下水径流模数法[2]、水均衡原理[3]等，但由于影响隧洞涌水的因素很多，这些理论方法往往忽略了大多数定性因素，理论方法的简化计算过程显然不能满足灾害发生的随机性[4-5]，导致预测涌水量与实际涌水量存在较大差距。同时，部分研究采用隧道涌水量预测模型试验[6]与隧道三维数值模拟分析[7-8]等方法进行涌水量计算，以获得较好的最大涌水量及发生位置； 但由于试验模型和数值模拟模型中对隧道工程的复杂工程地质条件和水文地质条件进行了很大程度上的简化或消除，也导致预测涌水量与实际涌水量存在显著差距。

因此，大多数隧道涌水量预测研究主要考虑采用随机性方法，从多因素的角度，结合定量和定性2类因素指标建立数学分析模型。贺小勇等[9]以地形、岩性、地质构造3个因素为基础，构建了不同的地质结构和隧道空间展布，对集水面积进行了预测分析； 郭锁山[10]采用层次分析法对浅埋偏压断层破碎隧道涌水量影响因素权重进行了分析，确定了对隧道涌水量有重大影响的关键因素，并排序了主次影响因素，提高了隧道涌水量预测计算精度； 廖志泓[11]以隧道6个里程段的地质构造和涌水情况为样本，建立了BP神经网络模型对隧道涌水量进行预测，得出最大相对误差在20%以内。

上述数学分析方法虽然取得了一定的效果，但这些方法用来确定权重的判断矩阵元素都是采用专家打分确定的具体数值，定性因素的随机性导致权重值的多解性使此类方法存在极大缺陷； 而模糊层次分析法(FAHP)恰能科学合理地分配各因素权重[12]，但其采用模糊数互反判断矩阵进行权重排序时，容易出现排序互斥问题，导致权重分配失衡。另外，为了预测涌水量的大小，现有研究方法主要为模糊综合评价法[13]，也存在依赖大量样本数据和评价模型训练修正过程复杂等缺陷。针对FAHP法和模糊综合评价的2类技术缺陷，本文提出采用平均优势度优化FAHP法的判断矩阵，并采用逼近理想解排序法(TOPSIS)替代模糊综合评价，能够根据有限评价对象与理想化目标接近程度进行综合评判。基于此，将优化FAHP-TOPSIS法应用于高压富水花岗岩隧道断层带涌水预测中，实现涌水等级及涌水量的准确预测。

1 优化FAHP法

FAHP法是通过建立一个由目标层、准则层和指标层构成的评价体系，逐层构成三角模糊数互反判断矩阵，进而得出权重； 但其采用模糊数互反判断矩阵进行权重排序时，容易出现排序互斥问题。因此，本文考虑采用平均优势度将模糊数互反判断矩阵优化为模糊数互补判断矩阵，以准确快速地进行权重计算。

1.1 由比较标度构造三角模糊数互反判断矩阵

表1 指标重要程度分级赋值标准

按照两两比较标度得到三角模糊数互反判断矩阵

(1)

1.2 平均优势度优化的FAHP法

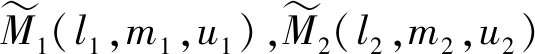
(2)

式中：l为模糊数下限值；m为最大可能性值；u为模糊数上限值。

(3)

则利用平均优势度优化FAHP法的三角模糊数互反判断矩阵为三角模糊互补矩阵的步骤如下。

1)采用简单加权法则集结专家们给出的各因素模糊数，计算每个因素的模糊综合评价值

(4)

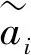
(5)

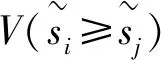
4)对模糊互补判断矩阵B，利用模糊互补矩阵排序的中转法(见式(6)[9])，计算其权重向量

(6)

1.3 隶属函数

1)定量因素的隶属函数(αi(x))采用偏大型半梯形分布函数，其函数形式如图1所示。

2)定性因素需要转化为确切的数值，采用德尔菲法[10]，其公式如下：

(7)

式中：N为评分专家总人数；pi为所有专家评分的平均值；di为所有小于pi评分的平均值；gi为所有大于pi评分的平均值。

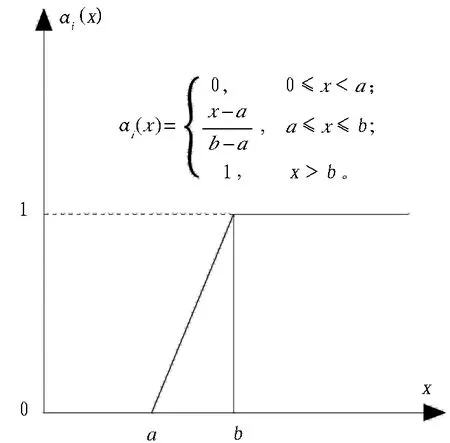
图1 偏大型半梯形隶属函数

2 优化FAHP-TOPSIS法

TOPSIS法的基本原理是借助多目标决策问题中的正理想解和负理想解的距离来对评判对象进行排序[14-15]。正理想解的各个指标均达到最优，可以理解为一个虚拟的最优解，而负理想解与之完全相反。TOPSIS法根据评判对象与理想化目标的接近程度进行排序，对现有对象进行相对优劣的评价，若评判对象最靠近正理想解，则为最优值，否则为最差值[16]。TOPSIS法算法模型计算过程如下。

2.1 初始评判矩阵

定义方案集Z={Z1,Z2,…,Zm}，每个方案Zi的评判指标集r={r1,r2,…,rn}，根据FAHP法中各指标的隶属函数确定其隶属值，得到初始评判矩阵

(8)

式中：rij为评判指标，定义为第i个方案的第j个指标，i∈[1,m]，j∈[1,n]；m，n分别为方案集Z和评判指标集r的元素数量。

2.2 加权评判矩阵

根据TOPSIS理论，将初始评判矩阵Z与FAHP法的指标层层次总排序权重矩阵Wn进行加权乘法运算，可得加权评判矩阵

(9)

式中Wj为FAHP法中指标层第j层次的总排序权重值。

2.3 贴近度分析

对加权评判矩阵R进行贴近度分析计算。其中正理想解R+为矩阵R行向量的最大值，负理想解R-为矩阵R行向量的最小值，表示为：

R+={[max(wjrij|i=1,2,…，m|j∈J+)],[min(wjrij|i=1,2,…，m|j∈J-)]} ；

(10)

R-={[min(wjrij|i=1,2,…，m|j∈J+)],[max(wjrij|i=1,2,…，m|j∈J-)]} 。

(11)

式中：J+={1,2，…，n}，为收益性指标；J-={1,2，…，n}，为消费性指标。

评判对象与理想解的距离为：

(12)

(13)

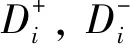
贴近度分析的计算公式为：

(14)

2.4 优化FAHP-TOPSIS计算模型

由TOPSIS法的贴近度分析构造出评判矩阵，结合优化FAHP法计算得到的权重，评判对象综合评判结果向量

Q=W×C。

(15)

式中：C为各评判对象与正理想解的贴近度评判矩阵；W为优化FAHP法计算得到的准则层权重。

3 工程应用

3.1 高压富水花岗岩隧道工程涌水情况

花岗岩质龙津溪隧道沿线穿越大、小断层共18处，其中代表性的断层包括F51： 宽1.5～2.0 m，充填碎裂岩，含水层渗透系数0.17 m/d。F55： 宽1～3 m，充填碎裂岩，带内岩体极破碎，含水层渗透系数0.23 m/d。F46： 宽5.1 m，充填碎裂岩，局部见断层泥，周围岩体节理发育，岩石破碎，含水层渗透系数0.18 m/d。F63： 宽2.3～2.7 m，充填碎裂岩，岩石完整性好，保水性好，含水层渗透系数0.2 m/d。F19： 宽2～3 m，充填碎裂岩，带内岩石极破碎，含水层渗透系数0.20 m/d。F56： 宽3～6 m，充填碎裂岩，局部见断层泥，含水层渗透系数0.23 m/d。

选取隧道K1+602～+640区段(S1)、K2+881～K3+011区段(S2)、K3+510～+600区段(S3)、K6+915～+995区段(S4)、K0+915～+985区段(S5)、K7+869～+982区段(S6)为研究对象，进行涌突水风险等级及涌水量预测。其中S1区段在K1+635处穿越断层F51，涌水量达212 m3/h； S2区段在K2+960处穿越断层F55，涌水量达675 m3/h； S3区段在K3+550处穿越断层F46，涌水量达715 m3/h； S4区段在K6+945处穿越断层F63，涌水量达408 m3/h； S5区段在K0+950处穿越断层F19，涌水量达380 m3/h； S6区段在K7+925处穿越断层F56，涌水量达438.5 m3/h。典型涌水状况如图2所示。

图2 隧道穿越断层带涌水情况

3.2 花岗岩断层带涌水层次结构分析

花岗岩断层带属于典型的构造运动深切性长大破碎带，呈现深厚残积土夹强风化岩块状，具有松散多孔、导水、导气、高压富水等特性。其涌水灾害具有孕灾结构特征的多样性、致灾因素的模糊性和因素值间的复杂非线性，使得致灾因素的识别难度巨大，在隶属权重的确定上具有一定的随意性。本文根据花岗岩断层带隧道工程特点，深入分析与隧道涌水灾害相关的多重影响因素，认为需要考虑工程地质、水文地质和施工设计3个方面。在工程地质方面，断层受到岩性、充填物特征、压张扭性质、宽度4个独立因素控制；在水文地质方面，断层含水量、地表水量、地下水量、降雨量及含水层透水性5个独立因素决定了断层的水文地质特征；在施工设计方面，隧道施工工法、埋深、注浆加固情况、超前支护情况4个独立因素进一步决定了隧道突涌水的风险程度。各涌水致灾影响因素值，一些是定性的，一些是定量的。本文采用优化的FAHP法，根据工程地质、水文地质和施工设计3个准则层上共13个影响因素指标值，建立花岗岩断层带涌水发生的层次结构模型，如图3所示。

3.3 确定权重分配

对指标进行重要度评价，构造准则层P和指标层R各因素的模糊判断矩阵。A-B，B1-C，B2-C以及B3-C模糊判断矩阵分别如表2—5所示。

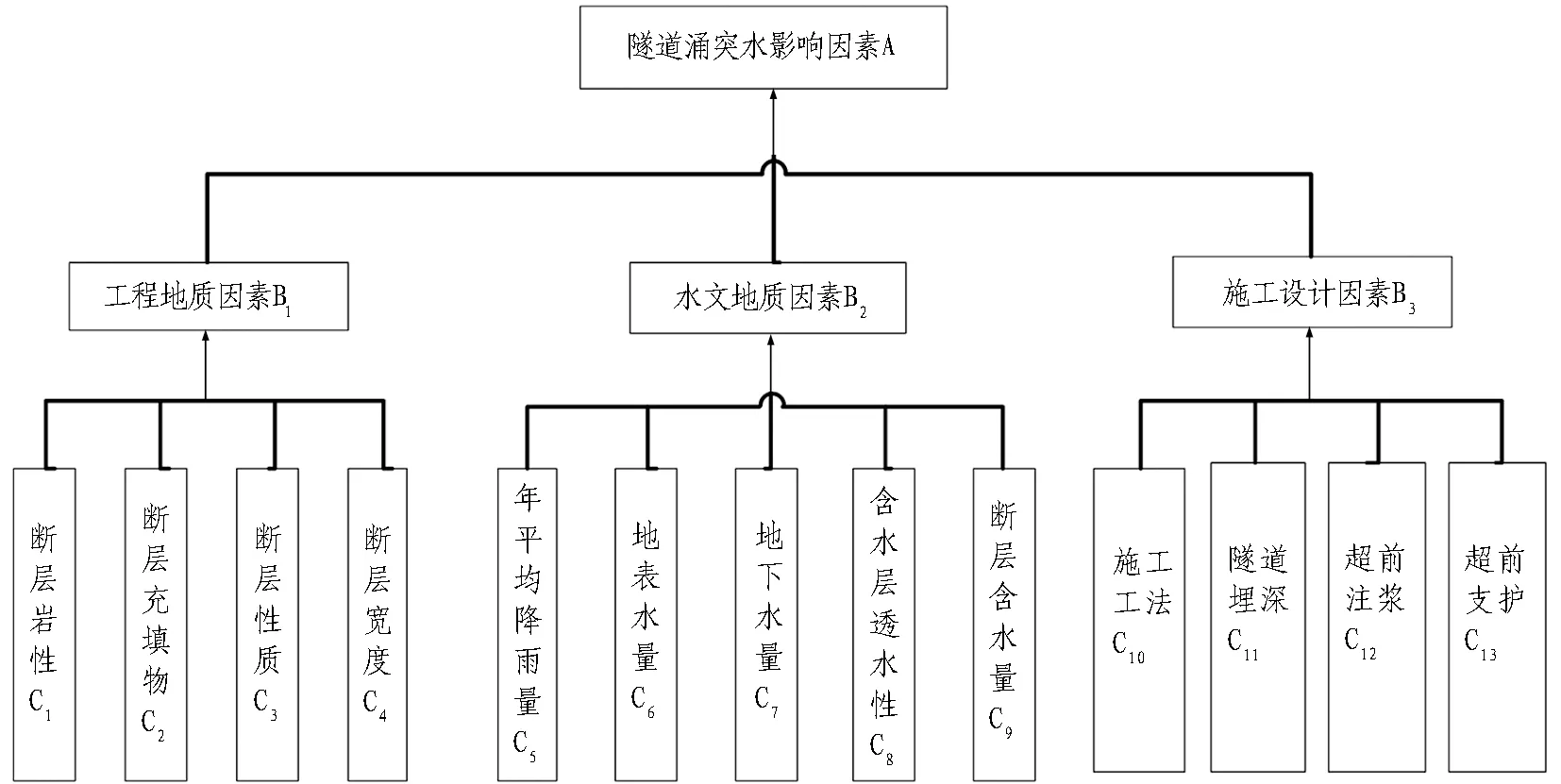
图3 评价指标层次结构图

表2 A-B模糊判断矩阵

表3 B1-C模糊判断矩阵

表4 B2-C模糊判断矩阵

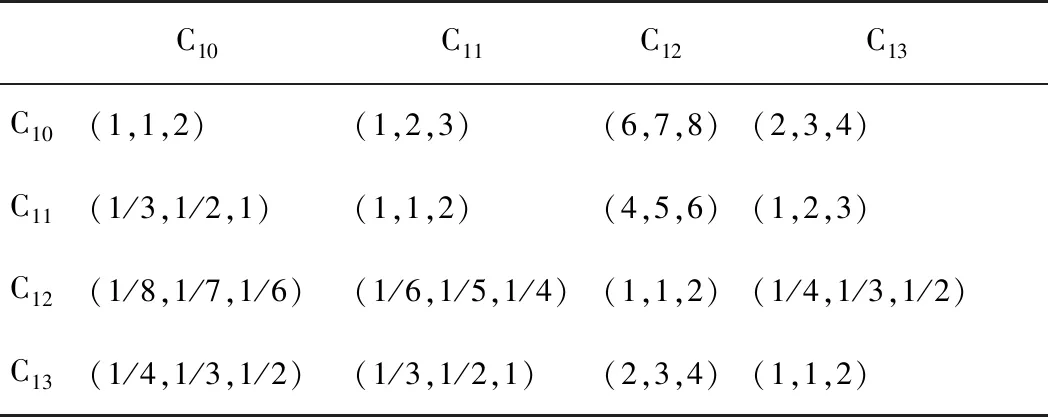
表5 B3-C模糊判断矩阵

根据表2—5计算可得： A-B矩阵一致性检验指标CR=0.055 9<0.1，满足一致性要求，权重矩阵W=(0.464 5,0.368 9,0.166 7)，可接受； B1-C、B2-C、B3-C矩阵一致性检验指标分别为CR=0<0.1、CR=0.001 2<0.1、CR=0.007 1<0.1，均满足一致性要求，权重矩阵分别为W1=(0.153 7,0.282 1,0.282 1,0.282 1)、W2=(0.132 9,0.132 9,0.261 8,0.213 1,0.259 3)、W3=(0.337 4,0.294 4,0.136 9,0.231 4)，均可接受。层次总排序结果见表6。

3.4 隶属函数评价准则与评价结果

花岗岩断层带涌水的13个致灾影响因素中，定量因素有4个： 断层宽度C4、年平均降雨量C5、含水层透水性C8、隧道埋深C11。其对应的偏大型半梯形隶属函数评价准则为：α4(x)[a,b,1,6]、α5(x)[a,b,200,1 000]、α8(x)[a,b,0.15,0.25]、α11(x)[a,b,100,400]。

表6 层次总排序结果

其他定性因素由德尔菲法确定的评价准则确定隶属函数值，在对所要预测的问题征得专家的意见之后，进行整理、归纳、统计，直至得到一致的意见，以此确定各因素的划分层级描述及其对应的隶属函数值区间，如表7—15所示。

表7定性因素C1隶属函数评价准则

Table 7 Membership function evaluation criterion of qualitative factor C1

C1α1(x)极坚硬岩 0～0.4坚硬岩0.4～0.6半坚硬岩0.6～0.8软岩、松散岩0.8～1

表8定性因素C2隶属函数评价准则

Table 8 Membership function evaluation criterion of qualitative factor C2

C2α2(x)角砾胶结0.2角砾多、断层泥少0.2～0.5角砾少、断层泥多0.5～0.8黏性土0.8～1

表9定性因素C3隶属函数评价准则

Table 9 Membership function evaluation criterion of qualitative factor C3

C3α3(x)压性0.2～0.5扭性0.5～0.8张、扭性0.8～0.9张性0.9～1

表10定性因素C6隶属函数评价准则

Table 10 Membership function evaluation criterion of qualitative factor C6

C6α6(x)无地表水补充0.3有少量地表水补充0.3～0.8大量地表水补充0.8～1

表11定性因素C7隶属函数评价准则

Table 11 Membership function evaluation criterion of qualitative factor C7

C7α7(x)贫水0.1～0.3弱0.3～0.6中等0.6～0.8丰富0.8～1

表12定性因素C9隶属函数评价准则

Table 12 Membership function evaluation criterion of qualitative factor C9

C9α9(x)少量0.1～0.2富水0.2～0.8强富水0.8～1

表13定性因素C10隶属函数评价准则

Table 13 Membership function evaluation criterion of qualitative factor C10

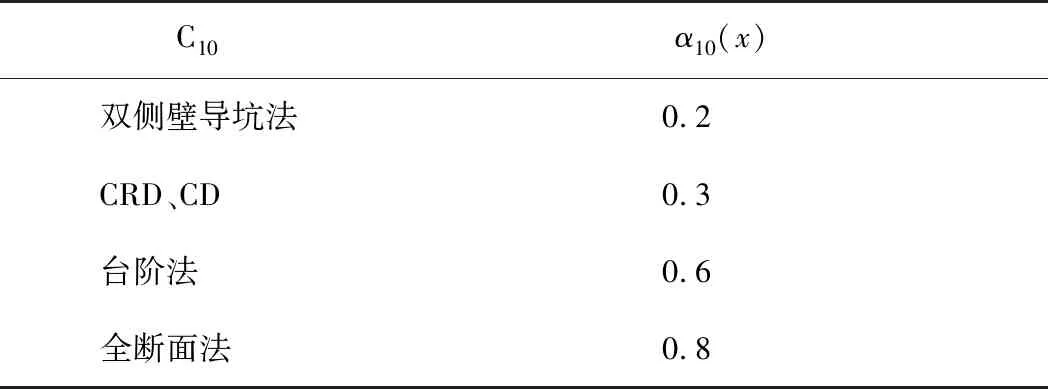
C10α10(x)双侧壁导坑法0.2CRD、CD0.3台阶法0.6全断面法0.8

表14定性因素C12隶属函数评价准则

Table 14 Membership function evaluation criterion of qualitative factor C12

C12α12(x)有0无1

表15定性因素C13隶属函数评价准则

Table 15 Membership function evaluation criterion of qualitative factor C13

C13α13(x)超前大管棚+小导管0.1超前小导管0.4超前锚杆0.7

根据工程地质勘察、设计施工类规范，隧道渗水涌水量等级和状态无统一划分原则，涌水量大小也无统一评价指标。综合规范要求和隧道工程特点，隧道涌水程度可考虑划分为4个等级： 小涌水(渗水滴水)、中等涌水、大涌水、特大涌水。关宝树[17]根据国家级指南、标准对隧道的涌水量进行了分级，认为渗水量≤2．5 L/(min·m)(即渗水量状态为干燥或湿润，或渗水滴水)时，基本上可以认为是在无水条件下施工。据此设定S7区段代表小涌水(渗水滴水)的无水施工条件，其界限涌水量设为0。另外，结合数学分析模型上的研究成果及其他隧道涌水资料，隧道涌水风险等级及对应涌水量指标可综合划分为： 中等涌水(<480 m3/h)，大涌水(480～960 m3/h)，特大涌水(>960 m3/h)。因此，设定S8区段代表中等涌水—大涌水的界限施工条件，其界限涌水量为480 m3/h； S9区段代表大涌水—特大涌水界限施工条件，其界限涌水量为960 m3/h。S7、S8、S9区段涌水等级的隶属函数评价结果如表16所示，表示涌水等级的临界状态。

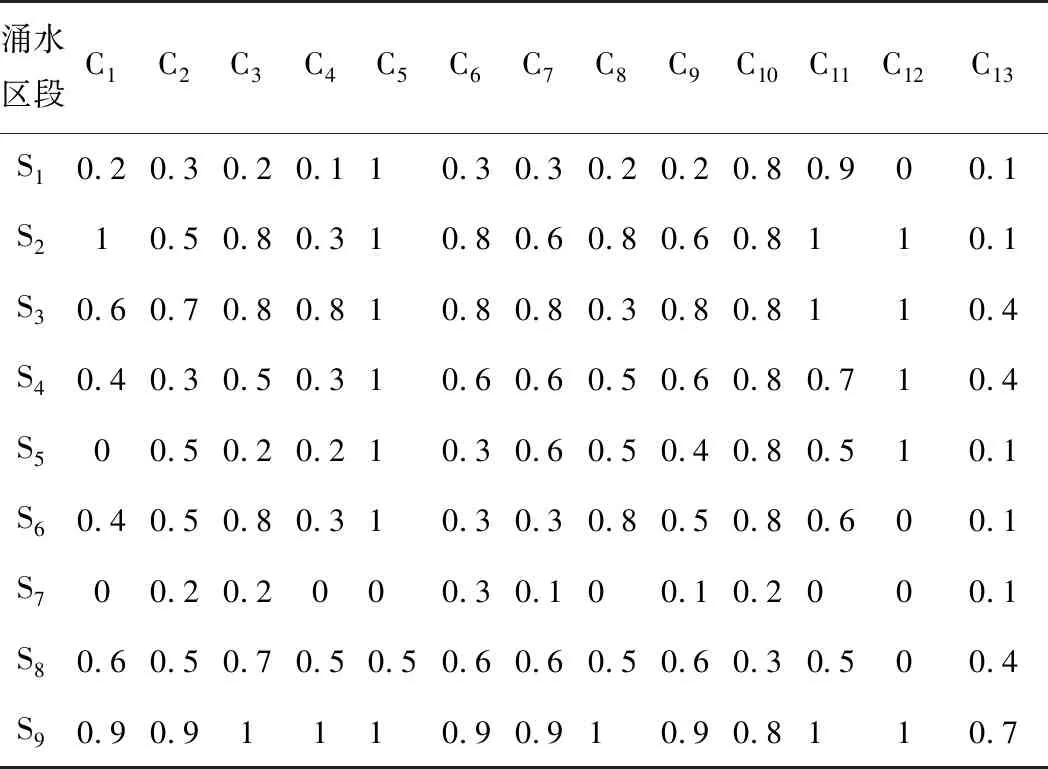
同时，根据各致灾影响因素隶属函数评价准则，确定S1—S9涌水区段隶属函数评价结果如表16所示。进而采用TOPSIS法评判模型进行涌水量预测。

表16涌水区段隶属函数评价结果

Table 16 Membership function evaluation results of water gushing section

涌水区段C1C2C3C4C5C6C7C8C9C10C11C12C13S10.20.30.20.110.30.30.20.20.80.900.1S210.50.80.310.80.60.80.60.8110.1S30.60.70.80.810.80.80.30.80.8110.4S40.40.30.50.310.60.60.50.60.80.710.4S500.50.20.210.30.60.50.40.80.510.1S60.40.50.80.310.30.30.80.50.80.600.1S700.20.2000.30.100.10.2000.1S80.60.50.70.50.50.60.60.50.60.30.500.4S90.90.91110.90.910.90.8110.7

3.5 涌水量预测

通过优化FAHP法计算得到的准则层B1—B3各评判指标的权重W={0.464,0.369,0.167}。

将W与C代入式(15)可得：

Q=W×C={0.281 0,0.629 7,0.732 0,0.496 5,0.394 5,0.504 7,0.030 7,0.522 5,0.984 2}。

综上，可得各涌水等级的综合评判结果分别为：QS1=0.281 0，QS2=0.629 7，QS3=0.732 0，QS4=0.496 5，QS5=0.394 5，QS6=0.504 7，QS7=0.030 7，QS8=0.522 5，QS9=0.984 2。

根据线性插值法可预测S1、S2、S3、S4、S5、S6区段涌水量分别为244、591、698、455、355、463 m3/h。其中S1、S4、S5、S6∈(S7,S8)，属于中等涌水； S2、S3∈(S8,S9)，属于大涌水。

4 预测涌水量和实测涌水量对比

为了验证优化FAHP-TOPSIS法在涌水量预测中的适用性，将预测涌水量与实测涌水量进行对比分析，得到预测涌水量与实测涌水量结果对比，如表17所示。

由表17可知，S1、S2、S3、S4、S5、S6区段的预测涌水量与实际涌水量间相对误差为14.8%、-12.4%、-2.4%，11.5%，-6.5%，5.6%，平均相对误差为8.87%，根据工程实际应用需求，此预测精度可满足工程施工准确性要求，说明本文提出的优化FAHP-TOPSIS法对于隧道穿越断层带涌水量预测具有适用性。

表17预测涌水量与实测涌水量对比

Table 17 Comparison of predicted water inflow and measured water inflow

涌水区段预测涌水量/(m3/h)实测涌水量/(m3/h)相对误差/%S124421414.8S2591675-12.4S3698715-2.4S445540811.5S5355380-6.5S6463438.55.6

5 结论与讨论

1)花岗岩断层带涌水灾害的致灾影响因素众多，本文从工程地质、水文地质和施工设计3个方面入手，创新性地提出花岗岩断层带涌水致灾的13个独立影响因素。

2)FAHP法采用模糊数互反判断矩阵进行权重排序时容易出现排序互斥问题。考虑采用平均优势度的定义将模糊数互反判断矩阵优化为模糊数互补判断矩阵的优化FAHP法，能够科学准确地进行多因素复杂层次结构模型的权重值分配。

3)优化FAHP-TOPSIS法将优化FAHP法的权重分配优势和TOPSIS法的评价矩阵优势相结合，通过精细化因素属性函数的评价——定量因素的偏大型半梯形分布函数和定性因素的德尔菲法函数，实现了花岗岩隧道断层带涌水的准确预测。

4)本文研究成果已成功应用于花岗岩隧道断层带涌水预测。但影响因素随着工程特性、地质特性、施工方法的不同，存在着较大的多样性，本研究成果仅仅是做了一定的探索与实际工程验证工作，更为广泛而深入的验证工作还有待进一步研究。