指数趋近律在冶金机器人机械臂轨迹跟踪中的应用研究

周军小

（抚顺矿务局职工工学院，辽宁 抚顺 113008）

1977年，V.I.Utkin首次提出了滑模变结构的概念，并进行了阐述。我国学者也相继进行了研究，并在此基础上进行了相关的演变，最具代表性的是高为炳，其在前人研究的基础上，第一次提出了趋近律的定义，并进行细化。文中使用的就是高为炳提出的指数趋近律。趋近律方法是把控制系统建立数学模型，把趋近律应用于数学模型，推演出控制律，应用于控制系统。

目前，冶金器人的应用领域比较广泛。如码垛、搬运、CNC上下料、焊接（氩弧焊和CO2气体保护焊）等；在金属零部件的加工、零件组装、整体搬运等；还有其它领域……，控制过程大体可以归纳为示教和在线两种方式。示教就是在机器人作业前，需引导机器人进行相关轨迹确认，机器人系统把每一步动作的坐标记录下来。在线就是机器人将操作者下达的命令记录下来，一步一步按照记录进行动作。由于机器人在线时按照设定好的路径进行运动，如果在运行中出现非正常的操作，除非操作者及时制止，否则机器人会一直按照设定轨迹走下去，有可能出现事故。

本文把指数趋近律应用于冶金机器人机械手臂的控制中，通过建立二阶数学模型，把推导出的控制律应用于二阶数学模型[1]，仿真后从图像中发现系统轨迹平滑，并在有限的时间内趋近滑模面，并具有较好的控制效果。

1 指数趋近律及相关

1.1 指数趋近律[2]

式（2）中引入了指数函数，在整个坐标系内是正值的可微函数，也是单调函数，这样为系统轨迹趋向滑模面提供了依据。从（2）中还可以看到求解后的表达式出现了一个常数项，从理论上来讲，系统轨迹是无法到达滑模面的，只是到达滑模面的上或下个单位的边界层。而在实际控制中，冶金机器人的机械手臂轨迹也不是非常精确，只要适当的将值变小，就可以应用到实际控制中。

对指数趋近律进行求解后，发现其能在有限的时间到达滑模面（系统正常运行的状态），接下来，对其到达条件进行验证。

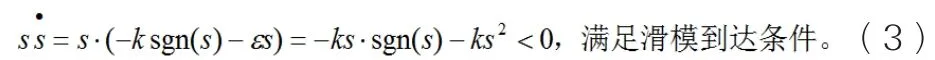
（3）只能证明指数趋近律用于控制系统中，能使系统达到正常运行的状态，至于能不能在有限的时间内趋近，还需要在对具体的参数方程进行仿真后说明。

冶金机器人系统是离散系统，设定采样周期为0.001s，将（1）离散化，推导出离散趋近律

离散趋近律的存在性和可达性条件

（4）说明，推导出的离散趋近律符合条件，及在有限的时间内趋近滑模面附近个边界层，也满足存在性和可达性条件。

1.2 离散控制律

从（3）中，可以得到离散控制律为

其中符号函数

通过引入符号函数，设定s(0 )=1分析得知，系统轨迹在时，才是单调递减，并且抖振较小，引起系统的振荡较小。（5）中，系统参数的ε和κ选择尤为重要，值太大，系统可能产生抖振；值太小，系统可能达不到预期控制效果。ε和κ值的选择，需在控制律和系统模型结合后进行调试设定。

2 离散趋近律应用于冶金机器人系统仿真实例

选择冶金机器人作为研究对象，这种机器人机械手臂有六个轴，统称为6自由度，分别为：腰关节、肩关节、肘关节、大臂、小臂和手腕。每个关节都可以自由的转动，选择合适的坐标达到控制效果。文中选择机器人的腰关节作为研究点，腰关节的坐标分为三种，直角坐标型、圆柱坐标型和球坐标型。其中直角坐标型是设定三个轴的坐标，即让腰关节在三维坐标下进行移动，这种坐标数据精确，移动位置准确，适用于食品行业和玻璃制品行业。

选择二阶离散系统进行仿真

仿真曲线如图所示：

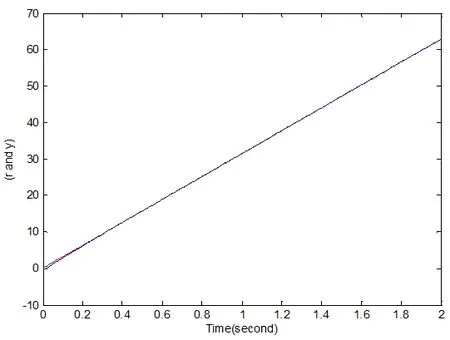
图1 跟踪信号曲线图

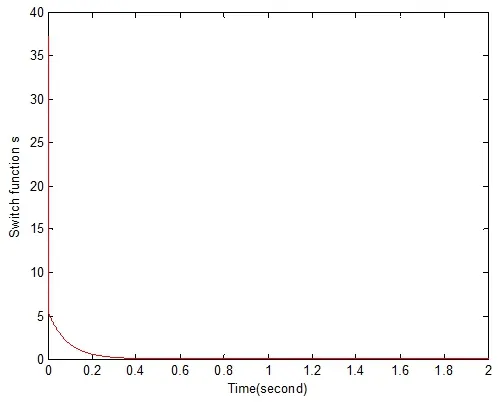
图2 控制输出曲线

从两个仿真图像来看，蓝色曲线是冶金机器人机械手臂的移动轨迹，红色曲线是新设计的控制律在对冶金机器人机械手臂移动的跟踪轨迹，坐标系显示，运动的初段，跟踪轨迹曲线在正常轨迹曲线的上下运动，当移动到中段时，正常移动曲线和跟踪曲线重合在一起，一起移动，误差不明显。从输出曲线来看，前段输出不太平滑，振动较大，中后段趋向平稳，并且比较光滑。

3 结论

本文基于滑模变结构中趋近律方法建立离散控制律，并对冶金机器人机械手臂建立二阶数学模型，首先对指数趋近律进行了计算，用数学的方法对其分析，接下来采用文献中的方法对系统轨迹在有限时间内到达滑模面和存在性和可达性条件进行了验证，从理论上证实了新趋近律的正确性。由于机器人控制系统是离散系统，所以对指数趋近律离散化，引入采样时间，其时间的选择根据建模仿真的结果进行优化。最后选取了一个典型的二阶系统，并列出了状态方程，在不断的仿真后，发现冶金机器人机械手臂的移动曲线和增加了新控制律的机械手臂的移动曲线在后段重合，跟踪效果较好，输出曲线也和原有输出曲线重合，证实了指数趋近律可以应用在冶金机器人机械手臂的轨迹控制中。