新型中空旋转平台的工业机械手上的应用

李 猛

（湖南华菱湘潭钢铁有限公司，湖南 湘潭 411101）

工业机械手是一种面向工业领域的多自由度的、多关节的、能自动化作业、靠机器手自身动力和控制技术来完成各种功能或动作的一种机器设备[1]。而中空旋转平台又普遍在机械手中得到应用。

中空旋转平台又称为旋转工作台，普遍应用于数控分度装置、机械手关节、机床第四加工轴及自动化生产线等旋转运动场合。中空旋转平台具有中空转盘结构、高刚性、高旋转精度及低成本等优点。且其重复定位精度介于凸轮分割器和DD马达之间，很多场合可以完美替代DD马达[2]。但某些场合中机械手在中空旋转平台处不仅要实现分度动作，还需要实现直线动作，但目前的大部分中空旋转平台并不支持直线动作，仅能做分度动作。因此本文设计了一种新型中空旋转平台来实现该功能需求，该产品同时能满足分度动作和直线动作。

1 新型中空旋转平台设计介绍

新型中空旋转平台需要在普通中空旋转平台上添加滚珠花键机构，如果采用同轴输入或旁轴输入式中空旋转平台时将难以实现分度动作和直线动作，而直角输入式中空旋转平台则可以满足要求。由于直角输入式中空旋转平台的电机输入轴与转盘轴垂直，因此需要采用蜗轮蜗杆传动形式的减速机构。蜗轮蜗杆由伺服电机驱动，其结构参考图1。图中伺服电机通过弹性联轴器来连接蜗杆轴，由蜗杆传动蜗轮，采用一级减速方式，而蜗轮则是固定在交叉滚子轴承上，而转盘固定在蜗轮上，转盘实际上就是由滚珠花键的花键套来替代的，该方案将滚珠花键的花键套集成在了中空旋转平台上，大幅度减小了体积。

2 新型平台的蜗轮蜗杆尺寸设计

由于蜗轮蜗杆机构是该中空旋转平台的核心机构，因此需要对其进行详细设计。本文以某型中空旋转平台为样本进行分析。选择其传动比i=62，蜗杆头数取Z1=1。伺服电机功率为P=100W，在结合了伺服电机的情况下可以实现大范围的调速。

蜗轮转矩T2按如下公式计算[3]：

式1中T2为蜗轮转矩；P为电机功率；n2为蜗轮转速；η为蜗轮蜗杆传动效率，按蜗杆头数为1时的标准取η=0.75。

则：

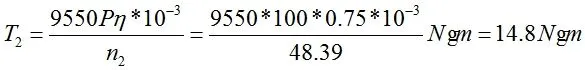
许用接接触应力按如下公式计算[3]：

蜗轮蜗杆模数按如下公式计算[3]：

式3中m为蜗轮模数；Z2为蜗轮齿数；[σ]H为许用接触应力；K为载荷系数；T2为蜗轮转矩；d1为蜗杆分度圆直径。

蜗轮齿面接触强度按如下公式校核[3]：

则有：

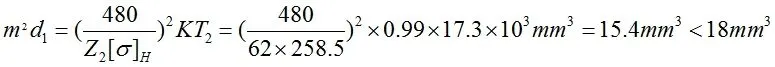
因此蜗轮齿面接触强度合格。

查机械设计手册取m=1mm，d1=18mm，m2d1=18mm3，接近以上计算值。

查机械设计手册按i=62，m=1mm，d1=18mm来确定蜗轮蜗杆的基本参数可得：中心距a=40mm；蜗杆头数Z1=1；蜗轮齿数Z2=62；蜗轮变位系数x2=0；蜗轮分度圆直径d2=mZ2=1＊62mm=62mm

对于蜗轮蜗杆而言，蜗轮的齿根易产生应力集中的情况，因此需要校核其齿根部位的抗弯强度，按如下公式校核[3]：

式5中σF为弯曲应力；K为载荷系数；T2为蜗轮转矩；γ为蜗杆导程角；d1为蜗杆分度圆直径；d2为蜗轮分度圆直径；m为蜗轮模数；YF为蜗轮齿形系数。

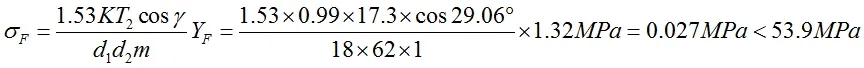
因此蜗轮齿根抗弯强度满足要求。

统计以上计算结果如下：蜗轮蜗杆中心距a=40mm，蜗杆头数Z1=1，蜗轮齿数Z2=62，蜗轮模数m=1，蜗轮变位系数X2=0，齿形系数a=20°，蜗杆分度圆直径d1=18mm，蜗轮分度圆直径d2=62mm。根据以上计算结果来计算蜗轮蜗杆的详细几何尺寸数据如下：

蜗杆几何尺寸：

圆整后取b1=20mm

蜗轮几何尺寸：

取b2=15mm。

3 新型中空旋转平台内部结构设计

上文介绍了蜗轮蜗杆的详细设计，在确定了蜗轮蜗杆的几何尺寸后需要匹配相应的轴承及执行机构。采用交叉滚子轴承来代替传统轴承，另外采用了滚珠花键来作为执行机构。其中交叉滚子轴承用来支撑蜗轮。

由于交叉滚子轴承的滚柱为交叉排列，其刚度好，因此只需要使用一套交叉滚柱轴环就就可承受各个方向的扭矩和载荷，从而大大减小了结构尺寸，采用的交叉滚子轴承型号选用XRU2012。下图2中空旋转平台内部结构。图中滚珠花键套是套在蜗轮内并通过螺钉固定。交叉滚子轴承外圈通过螺栓固定在中空旋转平台的箱体底部面上，而蜗轮则是通过螺钉固定到交叉滚子轴承的内圈上。滚珠花键由滚珠花键轴和滚珠花键套构成，是一种类似直线轴承的可导向的精密结构，并可以用来传递扭矩。其结构紧凑，能传递较大的载荷和扭矩。由于滚珠花键套里安装的是精密加工的滚珠，因此相比传统意义的滑动轴套而言有较低的摩擦系数和高精度，被广泛应用于精密数控机床和数控设备上。本文中滚珠花键套实际上就是转盘，在实现分度功能的同时可以实现花键轴的升降功能。

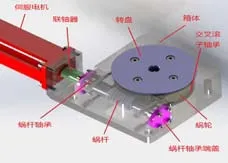
图1 直角输入式中空旋转平台结构

图2 中空旋转平台内部结构

蜗杆装配包含了蜗杆套、蜗杆轴、键、轴承端盖、弹性挡圈、定位隔套、蜗杆座及轴承等。图3蜗杆装配的剖面图。其中蜗杆用来传动蜗轮，蜗杆通过弹性联轴器与电机连接。轴承由隔套、挡性挡圈和联轴器等定位。考虑到蜗轮蜗杆的安装方便，蜗杆座从中空旋转平台的箱体上分离出来，用来安装蜗杆装配。蜗杆座通过螺钉固定到箱体上。考虑到蜗杆的可安装性，故将蜗杆分离成蜗杆套与蜗杆轴，通过键和定位隔套来定位。

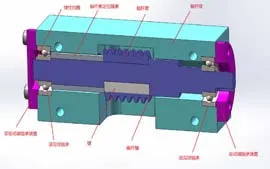
图3 蜗杆装配结构

图4 蜗轮蜗杆网格图

4 蜗轮蜗杆有限元分析

前文对蜗轮蜗杆的齿面接触强度和齿根弯曲强度进行了计算。另外将会使用有限元法对蜗轮蜗杆进行受力分析。有限元法是将分析的结构分成有限数量个的小单元体，单元与单元之间仅在有限个结点上相连，这样单元集合体可以近似代替结构，当单元越小时，其近似程度就越高。在有限元法中，结构的材料性能都可以在单元中保留，复杂的结构、边界条件及载荷情况都可很方便的处理，使得其成为目前结构分析的主流方法。

本文中采用了Solidworks里的Simulation有限元分析功能插件。Simulation用作有限元分析时较其它有限元分析软件有着操作简单的优势。

对蜗轮内圈进行固定约束，对蜗杆内圈进行水平移动和轴向移动约束，留一个转动自由度，蜗轮与蜗杆之间零件约束选择无穿透，然后在蜗杆内圈施加0.32Nm的扭矩。对蜗轮蜗杆装配进行网格划分，在蜗轮与蜗杆接触部位的齿面进行网格控制并形成网格图。一般网格划分得越小，计算过程会消耗较长时间，特别是对于较复杂的结构或复杂的装配体。因此划分网格时可以对总体网格划分得粗一些，然后对重要部位进行网格控制，这样能在相对较快的时间内得出结果，如图4网格图。

分析结果参考图5蜗轮蜗杆应力云图。计算结果显示蜗轮的齿根处应力为最大，最大值为171MPa。由于蜗轮的屈服应力强度为250MPa，因此强度满足要求。而蜗杆的齿根处应力为最大，最大值为202.8MPa。由于蜗杆的屈服应力强度为380MPa，因此强度满足要求。因此所设计的蜗轮蜗杆强度上能满足使用要求。

图5 蜗轮蜗杆应力云图

5 新型中空旋转平台的应用

该设计的中空旋转平台集成了滚珠花键套，显著缩小了设备体积及转动惯量。由于其集成了滚珠花键，因此只需要与其它机构适配就可以适用于机械手设备来同时实现分度功能和直线移动功能。特别是在滚珠花键轴采用中空结构的情况下还可以适配真空吸盘实现货物的抓取[4]。同时该中空旋转平台也可以作为分度转盘使用来代替普通中空旋转平台。而且在配合了伺服电机使用的情况下可以实现大范围的变速功能，因此其适配性非常强，可以进行推广使用。

6 结语

本文主要对新型中空旋转平台及滚珠花键进行了介绍和结构设计。此型中空旋转平台在传统中空旋转平台的基础上结合了滚珠花键能同时实现旋转和直线运动。有着较高的定位精度，且结构紧凑，体积小，承载大。由于将滚珠花键集成在了中空旋转平台中，减轻了蜗轮的重量，降低了转动惯量，大大缩小了设备体积，具有较强的适配性。