多层防护服热传导求解

张吉发 王壮 王者

摘   要：为了避免工人在高温环境作业过程中被灼伤，本文探讨高温作业中工人的专业服装设计问题。本文对多层防护服热传导进行分析，在合理的假设下将问题转化为一维非稳态热传导问题，基于Fourier定律和能量守恒定律，建立基于热传导方程的温度分布模型，并给出初始条件，左边界Dirichlet边值条件，右边界Robin边值条件，以及各层交界面处热流密度相等和温度相等的耦合条件。为了便于求解，本文将连续的定解区域作时间空间网格离散化，在导热方向上等距的取若干离散点，并以热传导方程为基础建立基于有限差分法的热传导非稳态模型，以中心差分和隐式差分实现热传导方程在空间和时间的离散化，得到三对角线性方程组，并借助追赶法求解。

关键词：有限差分法  一维热传导方程  方程耦合  边界条件

中图分类号：O52                                    文献标识码：A                        文章编号：1674-098X（2019）02（a）-0246-02

高温作业对工作人员的身体构成一定的威胁，而多层防护服是实现人体与外界环境有效隔热、为人体提供热防护的重要手段。研究热防护服的热传导问题对于防护服的设计、最长高温工作时间的确定具有十分重要的意义。对于一维热传导问题的研究，文献[1]采用同伦分析法（HAM）求解半无限介质瞬态热传导问题，虽然在不同的热场中有广泛的应用，但是该方法只能单层介质。文献[2]采用有限元法和时间差分法对瞬态热传导问题进行优化设计和灵敏性分析，可以获得较高的精度，但是求解过程计算量大，时间复杂度高。本文采用的有限差分法便于求解，避免了求解复杂的偏微分方程;利用耦合方程可以实现多层材料的热传导问题求解，具有很高的实用性。

1  一维热传导非稳态模型

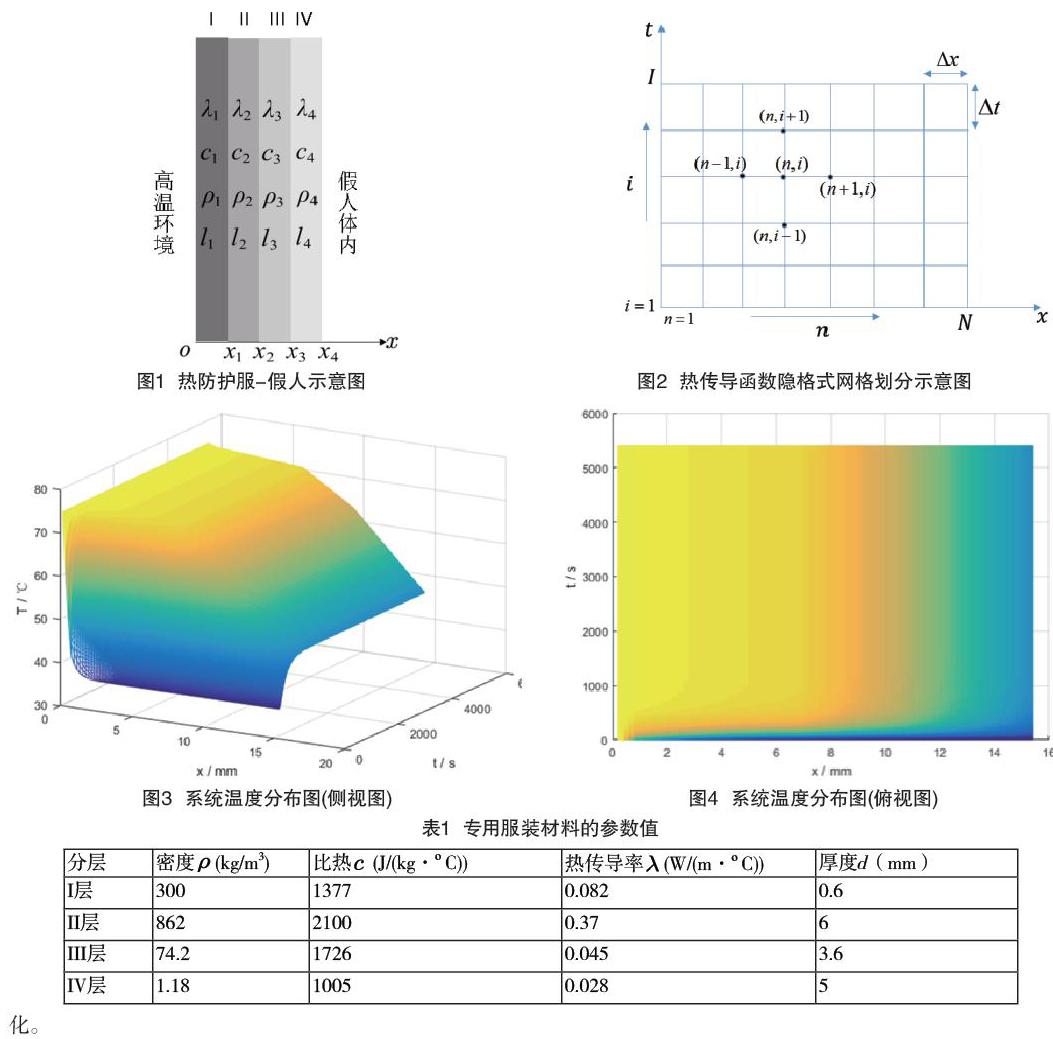
由于热防护服各层材料具有各向同性，且不考虑热辐射与热对流，所以多层防护服热传导问题可以简化为一维热传导问题，以衣服最外层为x轴坐标原点，x轴正方向指向人体内，做出如图1所示的示意图。其中，I、II、III为服装的三层织物材料，IV为III层与皮肤间的空气层，且I层与外界环境接触。并分别将I、II、III、IV层记为四层介质。防护服各层介质的热参数如表1所示。

1.1 热传导方程的确定

对于每一时间层，本文采用追赶法[4]求解三对角线性方程组，得到每一层的温度分布情况，进行迭代处理，求解下一时间层的温度分布情况。

从图3中可以得出，随着坐标值的增加，温度成梯度式下降。在8～12mm范围即第Ⅲ层和第Ⅳ层之间温度大幅变化。

3  模型的改进

本文只是研究了四层介质（包含空气层）的热传导问题，并没有考虑到皮肤作为一层介质也会对热传导问题产生影响，同时在建模過程中忽略了热辐射与热对流，这也会对求解结果产生一定的影响，如要得到更为精确地结果，热辐射与热对流应考虑在内。

对于偏微分方程的求解，本文采用了有限差分法，求解的精度随着划分时间空间网格点的数目的增加而增加，所以，可以划分更多的网格点以得到较高的精度。

4  结语

本文通过对热防护服的分析，在合理假设下将其转化为一维热传导问题，对各层介质列写热传导方程，对于各层交界面处，归纳出耦合方程，得出偏微分方程组，并总结出偏微分方程的初始条件和边界条件。对于复杂的偏微分方程的求解，本文采取了有限差分法，采用隐格式的后向差分，可以获得较高的精度和稳定性。可以采用更小的网格剖分步长已获得较高的精度。本文采用追赶法求解三对角线性方程组可以大大提高求解速度。

参考文献

[1] A·利扎尼亚，A·戈巴利，G·多麦利，等.半无限介质瞬态热传导的同伦分析法[J].应用数学和力学，2008，29（12）：1479-1485.

[2] 顾元宪，赵红兵，亢战，等.瞬态热传导问题的优化设计与灵敏度分析[J].大连理工大学学报，1999（2）：158-165.

[3] 杨世铭，陶文铨.传热学[M].4版.北京：高等教育出版社， 2006.

[4] 李文强，刘晓.追赶法并行求解循环三对角方程组[J].科技导报，2009，27（18）：90-93.