一种变结构电动汽车电子差速控制方法研究*

刘 恒宋伟奇韦彬贵

(1.柳州职业技术学院，广西 柳州545006;2.柳州城市职业学院，广西 柳州545036)

随着人们对环境改善的需求增加，近年来，电动汽车市场逐渐走俏，受到消费者的普遍欢迎.由于电动汽车采用电机替代传统的变速器、减速器等机械设备，不仅提高了传统效率，而且降低了环境污染.[1]由于电动汽车是通过电机对车轮的单独控制，其动力学特性独特，为了保证行驶的稳定性，需要精确的内外轮差速控制策略.[2]因此，电动汽车的电子差速控制技术成为该领域的热点研究内容.[3-5]

电子差速的基本原理是利用经典的控制方法对电动汽车驱动轮的精确控制，从而满足汽车运行的稳定性需求，提升车辆运行的稳定性和舒适性.[6]近十年来，国内外研究人员对电子差速的控制方法进行了深入的研究.例如，文献[7]基于传统的PID控制器，构建了四轮的差速约束方程，并实现了电子差速的精确控制，但是该控制方法要求时速低于10 km/h，且轮滑率小于预先设定的阈值;文献[8]将转速作为优化目标，采用门限阈值的方法对行驶车辆的滑移率和转向角进行控制，但是控制范围需要在设定的阈值范围内;文献[9]针对前轮驱动情况的差速系统展开研究，采用流量控制法实现了汽车转矩的自适应直接控制，并构建了用于实验验证的半实物平台.

纵观国内外研究现状，目前，电子差速控制主要集中在驱动轮的转速控制、滑移率的求解和转矩的解析表示三个方面，忽略了车辆整体状态的稳定性.因此，本文立足车辆稳态需求，针对车辆在快速转弯情况下的差速控制问题展开研究，在建立整车仿真模型的基础上，提出了基于横摆参量的滑模变结构控制方法.最后，基于构建的整车系统模型进行了详细的仿真分析，证明本文方法具有较优秀的控制性能.

1 模块化建模原理

1.1 轮毂电机模型

轮毂驱动电机模型是整车仿真的重要模块，模拟当前研究中通用的系统模型，采用永磁无刷直流电机构建驱动电机模型.假设输入电压为三相a、b、c，在a、b导通c断开的情况下，满足

可以将轮毂模型的平衡电压方程表示为

电磁转矩为

轮毂电机的动力学模型为

其中，U a、U b、U c为系统模型输入的三相电压值，e a、e b、e c为反电动势值，其系数为k e，i a、i b、i c为三相定子电流值，R为各相等值的电阻，各相绕组的自感与互感之差为L s-m，ωm、n p和k T分别表示电机的转速、极对数和转矩系数，J m为转动惯量，T L表示电机的负载转矩.

假设U=U a-U b，根据式(2)-(5)可以将转动电机的状态空间模型表示为

1.2 驾驶员运动模型

为构建整车仿真系统，构建驾驶员运动仿真模块是十分必要的，参考文献[10]的研究，构建如图1所示的运动系统模型.其系统的输入两为目标车速和实际车速的差值，输出参量为驱动轮毂的控制参量.为便于系统的稳定，在模型中引入了约束条件.

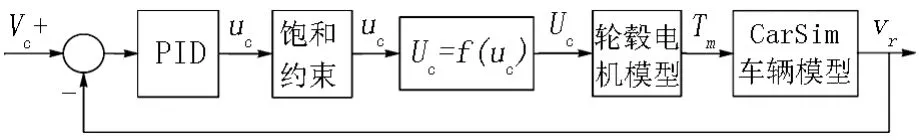
图1 驾驶员运动模型Fig.1 Driver Motion Model

2 提出的滑模变结构控制方法原理

2.1 车辆稳态横摆角速度参量

为便于推导横摆控制参量，采用如式(7)描述的线性而自由度模型

则横摆角速度参量对驱动轮转角输入的响应为

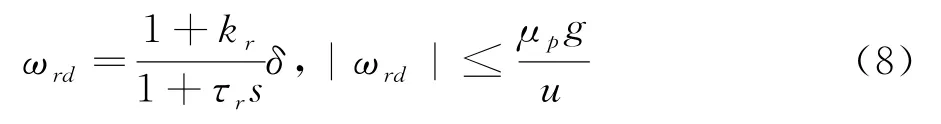
为了计算测量稳态参量，要求在稳态区域内，车辆侧向加速度满足a y＜μp g，进而可以将车辆稳态情况下的速度增益可以计算为

其中，K为稳定因子，式(7)～(9)中各参量的具体含义见表1.

表1 参量说明Tab.1 Description of parameters

2.2 电子差速的变结构控制设计

滑模变结构控制属于非线性控制问题，由于控制参量不是连续变化，可以对连续变化的非线性系统状态进行有节奏的优化和调整，进行保证目标轨迹控制在阈值范围内.同时，由于滑模变结构的状态参量与初始状态及外界扰动无关，因此具有非常高的稳定性.为便于分析变结构特性，可以将(7)式改写为

其中

一旦汽车进入滑动转台，其控制力矩可以计算为

计算误差

变化函数

变化函数的系数矩阵C=[c1]，为保证系统快速进入滑模状态，可以采用指数趋近的方式对轨迹进行限制，即

式中，ε为系统临近s=0时候的速度，σ为趋近速度的变化范围参量，为了防止切换过程中产生较大的抖动，采用传统的饱和函数sat替代目前研究中常用的切换函数sgn，进而可以将本文提出的滑模控制反馈参量表示为

其中

3 计算机仿真分析

3.1 仿真模型说明

为验证本文方法正确性和优越性，建立了如图2所示的整车仿真模型，仿真中具体参量的设置如表2所示.

3.2 仿真分析

针对构建的模型系统分析了车速60 km/h情况下的参量输入及变化控制情况，主要针对理想情况，不引入差速控制和本文方法控制的结果进行了对比.如图3、图4和图5所示.其中，图3为车辆行驶的仿真轨迹，主要是模拟在快速行驶状态下转弯情况的稳定性和差速的控制精度.从图3中曲线可以明显看出，在不引入电子差速控制情况下，其转弯半径要明显大于引入差速控制情况下的转弯半径，因此，引入本文差速控制方法以后，转弯性能得到了较大的改善和提升.其主要原因是，是因为引入差速控制以后，在转弯的情况下驱动力矩不再是平等分配，而是根据实际的附着要求自适应的调整.图4为驱动力矩的示意图曲线，从图4中可以看出，在左转的情况下，右侧(外侧)轮毂的转动力矩要明显大于左侧(内侧)的转动力矩，此时，测量的控制系统引入了横摆参量的控制，保持车辆的稳定性能.图5为横摆角速度的变化曲线，从图5中可以看出，横摆角速度的很好地拟合了理想状态，从整个曲线中可以明显看出本文方法的优点，不仅是相应的速度上，还是最后稳定的横摆参量值方面都维持在了最优的状态.当然，从图5中曲线也可以看出，稳定状态之前有一定的振荡和偏差，这主要是由于观测器本身的噪声引起，在后续的工程应用中可以通过增加滤波器的方式对稳态失调进行校正.

图2 仿真原理框图Fig.2 Simulating schematic block diagram

表2 仿真参数设置Tab.2 Settings of simulation parameters

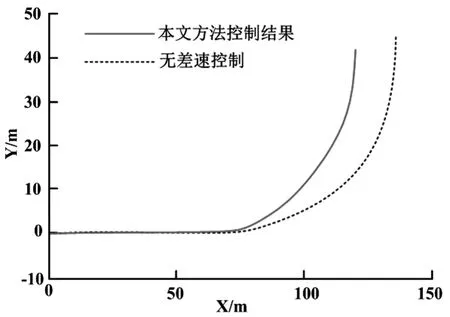
图3 仿真轨迹Fig.3 Simulation trajectory

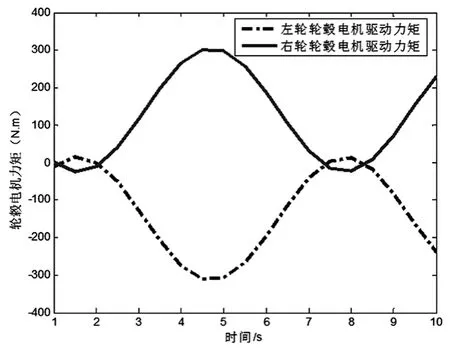
图4 驱动力矩曲线Fig.4 Driving Torque Curve

图5 横摆角速度变化曲线Fig.5 Yaw Angular Velocity Change Curve

4 结语

电动汽车已经成为当前绿色出行的首选代步工具，但是如何改善其运行的舒适性一直是业界研究的热点.本文主要基于转向情况下的车辆稳定性能需求，提出了一种模块化设计的变结构电子差速控制方法.构建了相应的轮毂电机模型和驾驶员运动模型，并分析了电子差速控制的参量方程，搭建了整车仿真系统.结果显示了本文方法在差速稳定控制方面的优势，保证了转弯状态的效果和稳定性.但是，也显示了该方法在状态变换时刻的稳态振荡问题，这一点需要在后续的研究中加以改善和研究.