一种导出R-H准则的方法*

陈绍荣，李晓毅，何 为，王 开

（陆军工程大学通信士官学校，重庆 400035）

0 引 言

在国内《信号与系统》著作中[1-2]，均介绍了R-H准则。文献[1]中，基于无源有耗网络阻抗函数的所有零点均位于s平面左半平面的事实，间接证明了R-H准则的正确性。本文在文献[3-4]的基础上，给出了一种导出R-H准则的方法。R-H准则遗留的问题：（1）在R-H阵列中，某一行的首元素为0时，如何完成R-H阵列的计算； （2）在R-H阵列中，某一行的元素全部为0的原因是什么，如何完成R-H阵列的计算，计算的结果对LTI连续时间系统的特征根分布是否存在影响。通过分析和讨论，本文将解决R-H准则遗留的相关问题。

1 R-H准则的有关引理

设n次多项式D(s)为：

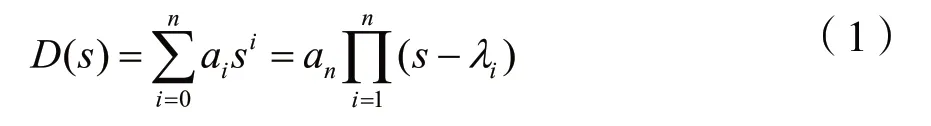
考虑到式（1），则有：

式（2）表明，D(-s)=0的根与D(s)=0的根在s平面上对虚轴互为镜像关系。

为了分析问题方便，现作下述定义：

将D(s)=0的根均位于s平面左半平面的多项式D(s)，称为霍尔维茨多项式，得到引理Ⅰ。

引理Ⅰ：D(s)为霍尔维茨多项式的充要条件是：

证明：首先证明充分性。若D(s)是霍尔维茨多项式，则式（4）成立。

考虑到式（1）和式（2），则式（3）可写成：

式中：

若λi与λi+1是D(s)=0的一对共轭根，考虑到 式（6），则Wi(s)与Wi+1(s)之积可表示成：

考虑到式（7），则Wi(s)可表示成：

设λi=αi+jβi，如 遇 实 根，则 取βi=0。考 虑 到s=σ+jω，由式（8）可得：

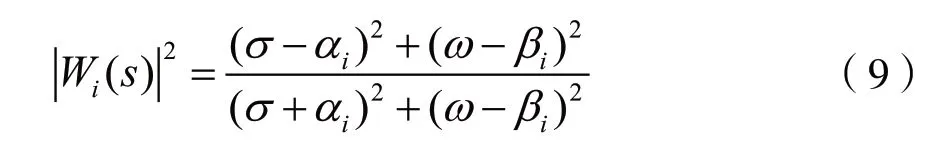
由于D(s)是霍尔维茨多项式，因此满足αi=Re[λi]＜0(i=1,2,…,n)。于是，有：

考虑到（10），由式（5）可得：

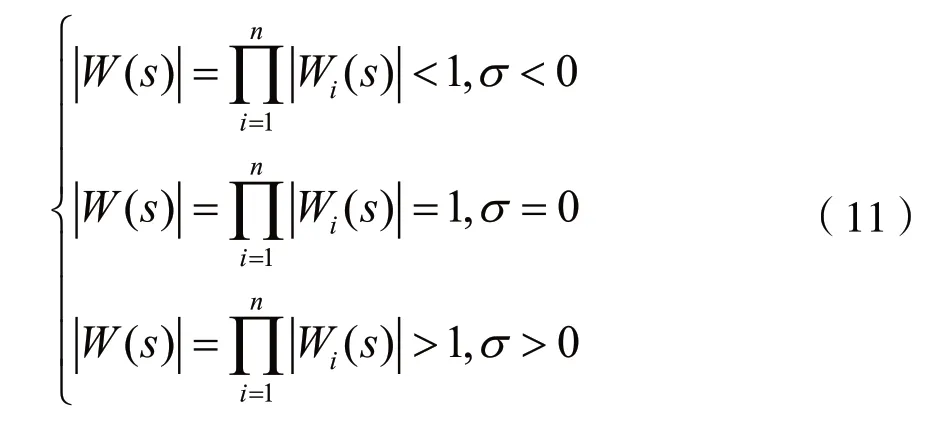
式（11）表明，若D(s)是霍尔维茨多项式，则式（4）成立。

再来证明必要性：若满足式（4），则D(s)是霍尔维茨多项式。

采用反证法证明。设D(s)不是霍尔维茨多项式，那么D(s)=0在s平面的右半平面内有根。由式（2）可知，D(-s)=0在s平面的左半平面内有根。由式（3）可知，W(s)在s平面的左半平面（σ＜0）内必有极点，在极点的邻域内，|W(s)|＞1，与式（4）相矛盾。

因此，式（4）是D(s)为霍尔维茨多项式的充要条件。

再定义：

由于Q(s)是偶次项之和De(s)与奇次项之和Do(s)之比，因此Q(s)的分子和分母最高次幂相差1。当n为偶数时，s=0和s=∞分别为Q(s)的单零点和单极点；当n为奇数时，s=0和s=∞分别为Q(s)的单极点和单零点。令s=jω，不论n为偶数还是奇数，则Q(jω)都是ω的虚奇函数。

考虑到式（3），则（12）可表示为：

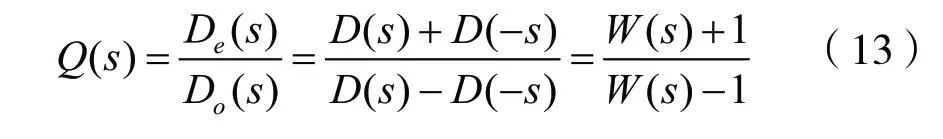
由式（13），得到引理Ⅱ。

引理Ⅱ：D(s)为霍尔维茨多项式的充要条件是：

证明：首先证明充分性。若D(s)是霍尔维茨多项式，则式（14）成立。

将W(s)用极坐标表示，即：

考虑到式（15），由式（13）可得：

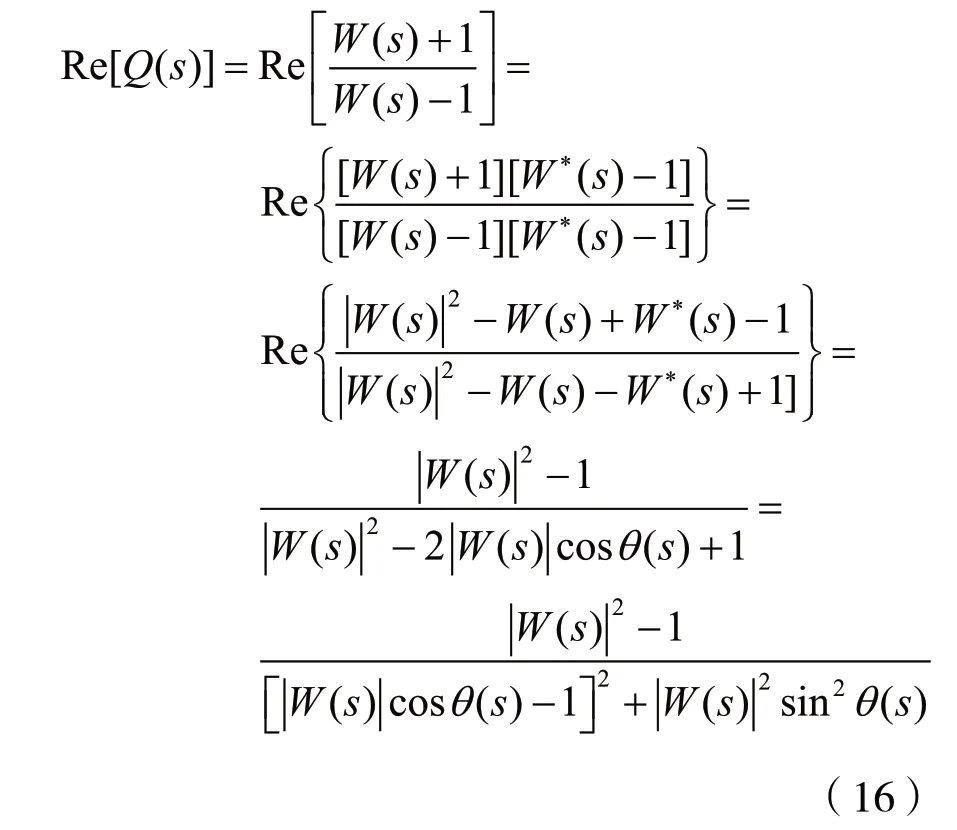
考虑到式（4），由式（16）可知，若D(s)是霍尔维茨多项式，则式（14）成立。

再来证明必要性：若满足式（14），则D(s)是霍尔维茨多项式。

采用反证法证明。设D(s)不是霍尔维茨多项式，那么D(s)=0在s平面的右半平面内有根。由式（2）可知，D(-s)=0在s平面的左半平面内有根。由式（3）可知，W(s)在s平面的左半平面（σ＜0）内必有极点，在极点的邻域内，|W(s)|＞1，由式（16）可知Re[Q(s)]＞0，这与式（14）相矛盾。

因此，式（14）是D(s)为霍尔维茨多项式的充要条件。

引理Ⅲ：D(s)为霍尔维茨多项式的充要条件是Q(s)仅在s平面的jω轴上有单极点，且有实的正 留数。

证明：先来证明充分性。若D(s)是霍尔维茨多项式，则Q(s)仅在s平面的jω轴上有单极点，且有实的正留数。

设Q(s)在s=s0处有m阶极点，则在s0的邻域内，可用式（17）任意地逼近Q(s)，即：

式中，k＞0，θ为实数，m为正整数。

又设s-s0=ρejφ(0≤φ≤2π)，则有：

由式（18）可知，在以s0为圆心、ρ为半径的圆周上，Re[Q(s)]的符号随着mφ的变化而变化。若D(s)是霍尔维茨多项式，由式（14）可知，在s平面的左半平面内或右半平面内，Re[Q(s)]的符号是不改变的。因此，Q(s)的极点s0不能位于s平面的左半平面内或右半平面内，只能位于s平面jω 轴上。

Q(s)在jω轴上的极点s0是否允许为多重极点？这是需要解决的一个问题。考虑在以s0为圆心、ρ为半径的圆周上，-π/2＜φ＜π/2与σ＞0等价，π/2＜φ＜3π/2与σ＜0等价，则式（14）可写成：

在式（18）中，若m＞1，即取m是大于1的整数，则Re[Q(s)]在以s0为圆心、ρ为半径的圆周上，将至少变四次符号，这与式（19）相违背。因此，在jω轴上不允许Q(s)有多重极点。如果m=1，满足式（19）的θ的唯一允许值为：

由于s0是Q(s)在虚轴上的一阶极点，则kejθ是它的留数，这就证明了若D(s)为霍尔维茨多项式，则Q(s)仅在s平面的jω轴上有单极点，且有实的正留数。

再来证明必要性：若Q(s)仅在s平面的jω轴上有实的正留数的单极点，则D(s)是霍尔维茨多 项式。

假设n为偶数，则式（12）可写成：

考虑到s=σ+jω，由式（21）可得：

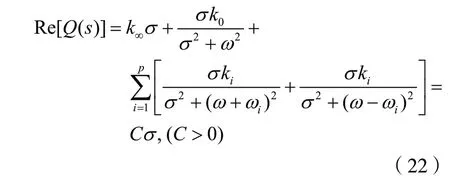
显然，式（22）满足式（14），也满足式（4）。

这样就证明了D(s)为霍尔维茨多项式的充要条件是Q(s)仅在s平面的jω轴上有实的正留数的单极点。

引理Ⅲ可作为检验的基础，即列出Q(s)并确定其极点位置，这些极点必是jω轴上的单阶极点，且留数为正实数，但仍需通过对Q(s)的分母进行因式分解才能确定jω轴上的这些单极点。

2 罗斯—霍尔维茨准则

2.1 霍尔维茨准则

设：

由式（24）可知，G(s)可以写成：

若D(s)为霍尔维茨多项式，由引理Ⅲ可知，C1＞0，且G1(s)可写成：

式中，k0＞0，ki＞0。

由式（24）和式（25）可知，若将G1(s)写成两个多项式之比，则分母多项式的次数只能比分子多项式的次数高一次，则1/G1(s)可写成：

式（26）表明，G1(s)也仅在s平面的jω轴上有单极点，且留数为正实数。由引理Ⅲ可知，式（27）中的C2＞0，且要求G2(s)也仅在s平面的jω轴上有单极点，且留数为正实数。

同理，有：

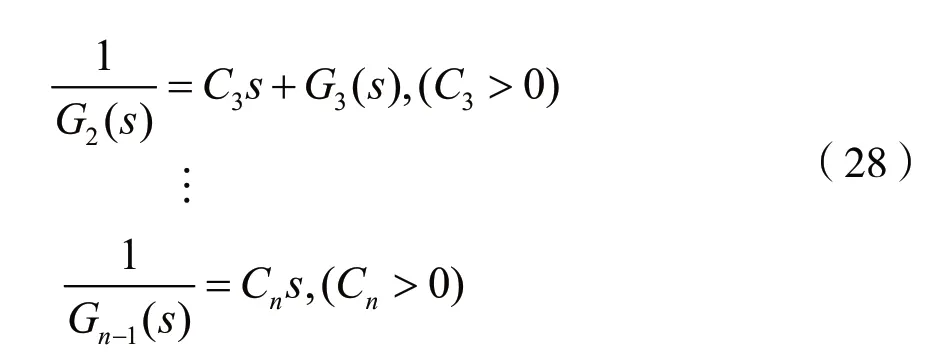
分析表明，若n阶LTI连续时间系统是一个因果稳定系统，则保证n次多项式D(s)=0的根均位于s平面左半平面的充要条件是：D(s)的偶次多项式之和De(s)与奇次多项式之和Do(s)辗转相除的商Ci(i=1,2,…,n)均为正值。反之，若D(s)=0的根均位于s平面的右半平面，则由引理Ⅰ和引理Ⅱ可知，式（18）中的θ、m只能分别取π和1。由引理Ⅲ和引理Ⅳ可知，Q(s)及1/Q(s)仅在s平面的jω轴上有单极点，且有实的负留数，也就是说，相应的n个Ci值均小于零。可见，Ci为正值、负值的个数与D(s)=0的根位于s平面左半平面、右半平面的数目相对应。

2.2 罗斯准则

考虑到式（24），有：

第一次长除，有：

显然：

第二次长除（辗转相除，用除数除以余数），有：

显然：

由此得到罗斯阵列或称R-H阵列，即：

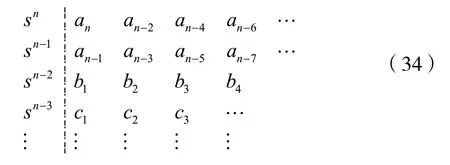
这个阵列的第一行和第二行是多项式D(s)各幂次的系数的交替排列，其余各行是通过辗转相除运算后得到的。第一行除以第二行的商为C1s(C1=an/an-1)，所得的余部构成阵列的第三行，且第三行的列元素比前两行的列元素少1；第二行除以第三行的商为C2s(C2=an-1/b1)，所得的余部构成阵列的第四行，且第四行的列元素又自动减1，直到构成n+1行为止，其中n个Ci值为R-H阵列中第1列的n+1个元素交替之比。可见，n个Ci值为正值的等效判据是R-H阵列中第1列的元素应具有相同的符号。同时，根据霍尔维茨准则的结论可知，若R-H阵列中的第1列的元素有正有负，则相邻两个元素符号改变的总次数正好是D(s)=0的根位于s平面右半平面的数目。

3 特殊情况的处理

3.1 R-H阵列中某行的第一个元素为零，而其余元素不全为零

R-H阵列中某行的第一个元素为零，其余元素不全为零，可用下述三种方法进行处理。

（1）将此行的第一个元素用无穷小量ε代替，并继续排完整个R-H阵列。可以证明，第1列元素符号改变的总次数与ε（正与负）无关。

（2）将R-H阵列对应的多项式D(s)乘以因子(s+1)得到Dn+1(s)，展开Dn+1(s)再构成新的R-H阵列进行检验，可以避免出现上述情况。然而，Dn+1(s)=0与D(s)=0在s平面右半平面的根的个数相同。

（3）利用多项式D(s)构成一个相伴的倒数多项式D@(s)=snD(s-1)，对D@(s)用R-H阵列进行检验，可以避免出现上述情况。由复变函数的映射理论可知，D@(s)=0与D(s)=0在s平面右半平面的根的个数相同。

3.2 R-H阵列中出现全零行

这种情况发生在两个相邻行对应元素成比例时，实质是因为De(s)与Do(s)中有公因子A(s)所致。R-H阵列中，全零行的上一行就是这个公因子。若将多项式D(s)的最高幂次置于R-H阵列的第一行之前，并依次在下一行中降低幂次，则可将公因子A(s)找出来。由于A(s)是De(s)与Do(s)的公因子，而De(s)是全偶多项式，那么A(s)一定也是全偶多项式。因此，A(s)=0的根一定是关于原点对称分布的，且A(s)=0的根是D(s)=0的根的一部分。因此，R-H阵列中出现全零行是D(s)=0有零实部共轭根的必要条件（但非充分条件）。为了确定D(s)=0在s平面右半平面的根的数目，相应地也有下述三种处理方法。

（1）可用偶次多项式A(s)的导数A´(s)的系数代替全零行来完成整个R-H阵列的计算。利用Rouché定理可以证明，多项式A(s)+A´(s)并没有比多项式A(s)增加位于s平面右半平面根的数目。

（2）从R-H阵列中找出A(s)后，D(s)=A(s)DA(s)， 根据A(s)及A(s)之前的各行中的第一个元素，便可确定DA(s)=0的根的个数及其分布，而A(s)=0的根可用因式分解给出。

（3）从R-H阵列中找出A(s)后，对一些特殊的偶次多项式A(s)而言，可令A(s)中的重新构成多项式A0(p)，再用R-H阵列检验其根的分布，并注意A(s)=0的根关于原点对称分布的特点，即可确定A(s)=0的根的分布。

例1：设：

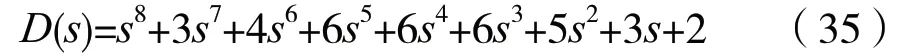
试确定D(s)=0的根的分布情况。

s解：R-H阵列为：

于 是A(s)=2s6+4s4+4s2+2，D(s)=A(s)DA(s)，显然：

即：

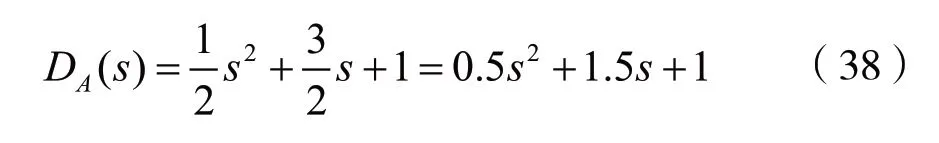
多项式DA(s)的R-H阵列如下：

可见，多项式DA(s)的R-H阵列中第1列的元素符号相同，故DA(s)=0的两根均在s平面的左半平面。

分析表明，从多项式D(s)的R-H阵列中得到的C1和C2的值与从多项式DA(s)的R-H阵列中得到的C1A和C2A的值相同，因此可直接采用多项式D(s)构成的R-H阵列中得到的C1和C2的值来确定DA(s)=0的根的分布情况。

综上所述，为了确定D(s)=0的根的分布情况，则确定A(s)=0的根的分布情况成为关键问题。解决A(s)=0的根的分布问题，通常有下述三种方法。

方法1：用A(s)的导数A´(s)的系数代替全零行，继续完成整个R-H阵列的计算。

注意，由于R-H阵列中的运算是行列式运算，某行乘以或除以一个正数，仅影响下一行各元素的大小，而不影响各元素的符号。

由于R-H阵列中第1列元素的符号改变了两次，故D(s)=A(s)DA(s)=0有两个根位于s平面的右半平面。又因为DA(s)=0的两个根均位于s平面的左半平面，故A(s)=0有两个根位于s平面的右半平面。

则有：

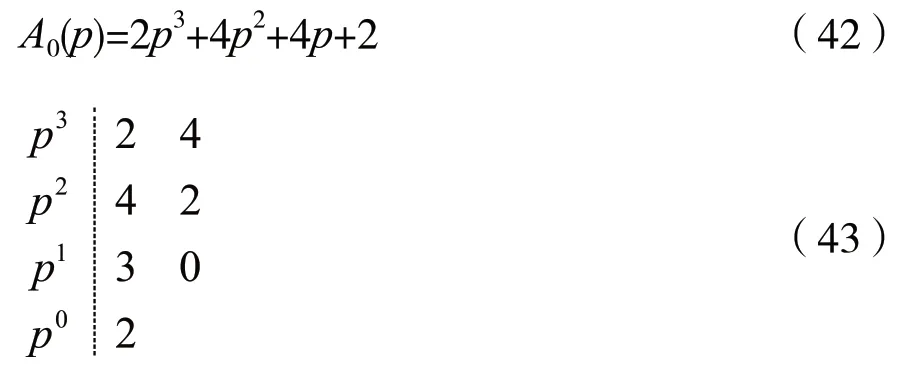
因R-H阵列中第1列元素的符号相同，故A0(p)=0的根均位于p平面的左半平面。又因A0(p)是三次（奇次）多项式，故A0(p)=0一定有一个负实根，那么A(s)=0在s平面的jω轴上一定有一对共轭虚根。考虑到A(s)是六次多项式及A(s)=0的根是关于原点对称分布的，那么A(s)=0在s平面的右半平面上一定有一对共轭复根。

方法3：通过对公因子偶次多项式A(s)进行因式分解来确定其根。

考虑到：

则有：

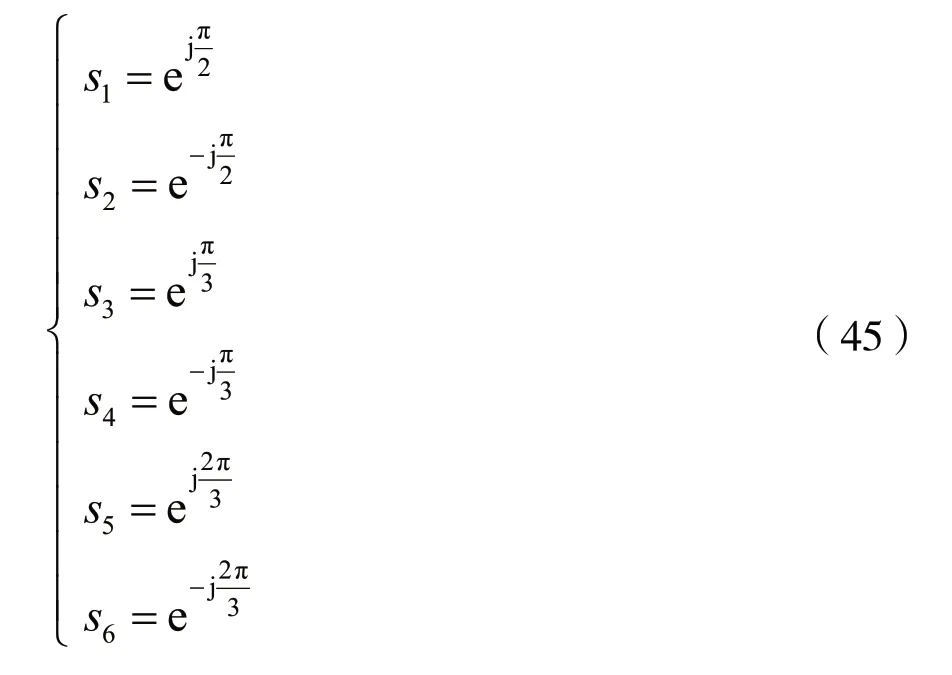
式（45）表明，A(s)=0的根在s平面上的分布不仅对称于原点，而且有一对共轭根位于s平面的右半平面。

4 结 语

本文在文献[3-4]的基础上，基于映射和留数的概念，给出了一种导出R-H准则的方法。针对R-H阵列中某一行的首元素为0的情况，给出了三种处理方法；针对R-H阵列中某一行的元素全部为0的情况，不仅剖析了原因，而且给出了三种处理方法，成功解决了R-H准则的遗留问题。