基于空间谱估计的终端AOA定位*

王冬海，张 海，张泽孜

（杰创智能科技股份有限公司，广东 广州 510663）

0 引 言

在公共安全领域，经常需要对已知电话号码的终端（User Equipment，UE）进行基于非合作接收的精确定位。所谓非合作接收指的是不需要手机做任何配合，也无需侵入网络侧获取数据，仅仅通过监听空口无线信号，完成对UE终端的无感定位。文献[1]对长期演进（Long Term Evolution，LTE）手机定位技术有很多介绍，包括蜂窝网定位，基于信号强度的定位，基于小区标识（Cell Identification，Cell ID）的定位，基于到达时间差（Time Difference of Arrival，TDOA）以及基于到达时间（Time of Arrival，TOA）的定位方法。以上定位方法需要通过测量相关信号参数获取手机的坐标，UE需要配合基站做定位参数测量，容易受各种干扰，定位精度差。文献[2]对各种定位方法的误差进行了具体分析。本文着眼点在于采用基于非合作接收技术的波达角（Angle Of Arrival，AOA）定位技术确定手机位置，提出了一种基于多重信号分类（Multiple Signal Classification，MUSIC）算法的空间谱估计的高精度波达方向（Direction Of Arrival，DOA） 算法。

对信号的到达方位角进行测量一般采用阵列天线。文献[3]采用8元均匀圆环阵，实现了多波束覆盖，同时兼顾粗略DOA估计。本文采用MUSIC经典空间谱估计算法，实现对终端上行信号的DOA估计，估计精度高，同时通过移动一定距离多次测量取平均值实现终端的AOA精确定位。

1 空间谱估计

1.1 均匀圆环阵

图1给出的是均匀圆环阵示意图。阵元均匀分布在XOY平面内半径为r的圆环上。圆环的圆心位于坐标原点O。均匀圆环阵可以同时分辨出方位角和俯仰角。

假设入射信号的方位角为θ，俯仰角为β，则以圆心作为参考点的均匀圆阵阵列流行向量表达 式为：

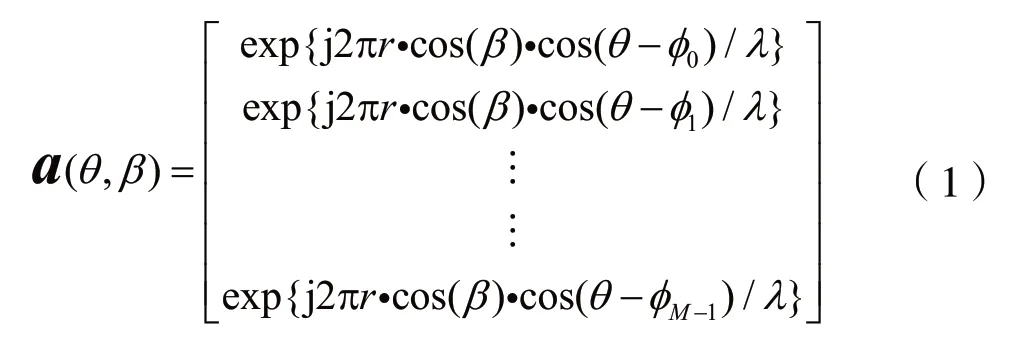
其中，mφ表示天线阵元与圆心所在直线的方位，对于均匀圆环阵而言，mφ=2πm/M，（0≤m≤M-1）。r/λ表示圆环阵半径与信号波长的比值，典型取值为0.5。虽然从形式上，a(θ,β)矩阵不具备Vandermonde结构，但是通过一些预处理可以转化成Vandermonde结构。

图1 均匀圆环阵示意图

指定期望波束的方位角和俯仰角，很容易得到式（1）的加权系数，如式（2）所示，其中1≤m≤M。

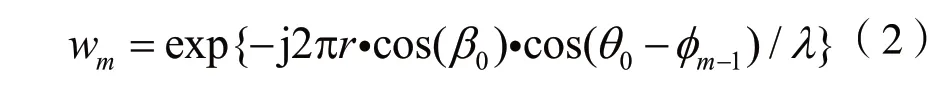
图2 八阵元均匀圆阵水平方向图

之所以采用均匀圆环阵是因为均匀圆环阵主瓣宽度与方位角无关，而且随着r/λ增大或者减少，不会出现明显的珊瓣效应，因此均匀圆环阵适应频带范围宽。

1.2 MUSIC算法与空间谱估计

MUSIC算法属于超分辨率算法。该算法不仅在参数估计方差上可以渐进逼近相应的克拉美罗界（CBR，Cramer-Rao Bound），而且其角度分辨能力也可以突破传统“瑞利限”的制约。MUSIC算法基于信号子空间和噪声子空间的概念，通过对阵列输出自相关矩阵进行特征值分解获得上述两两正交的子空间，并利用信号方位对应的阵列流行向量与噪声子空间相互正交的特性估计信号方位。

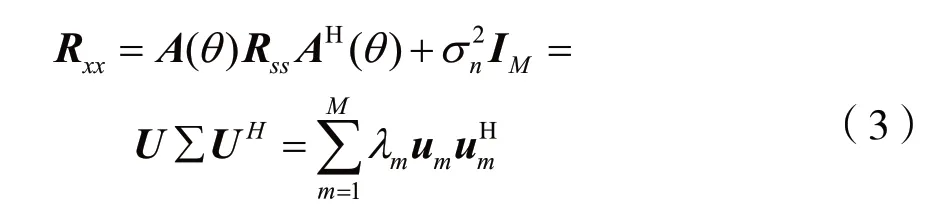
式（3）中Rxx为阵列输出自相关矩阵，也是Hermitain矩阵。U=[u1u2… uM]表示单位特征向量矩阵，Σ=diag[λ1λ2… λM]表示特征值对角矩阵。对特征值排序如式（4）所示。

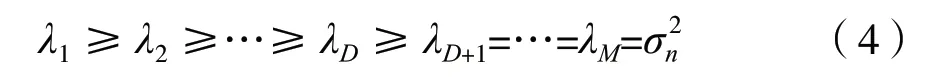
其最小的M-D个特征值均等于噪声功率σn2，记成ΣN=diag[λD+1λD+2… λM]=σn2IM-D，最大的D个特征值写成ΣS=diag[λ1λ2… λD]，M表示阵元个数，则式（3）可以写成式（5）的形式：

其中，US=[u1u2… uD]表示信号特征向量矩阵，UN=[uD+1uD+2… uM]表示噪声特征向量矩阵。

实际计算过程中，阵列输出自相关矩阵Rxx无法精确获得，只能通过有限数据样本近似估计，其最大似然估计为：

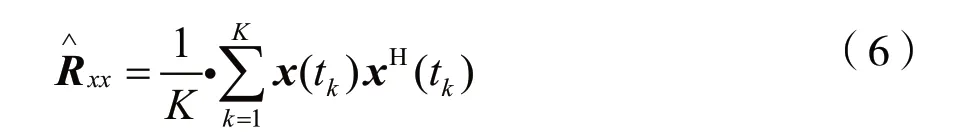
其中，K表示样本点数，对R^xx进行特征值分解，获得信号特征向量矩阵和噪声特征向量矩阵，统计学上有如下关系：

式中，Us与为一致估计。因此，在实际计算中，用得到如下优化准则：

2 DOA估计与AOA定位

2.1 UE上行信号

在对终端进行空间谱估计的时候，最难点在于如何分辨具体的信号来自哪一个UE终端。因为公网空口中随时存在大量终端与基站交互数据。在非合作接收技术中，以监控基站下行来获取终端上行信息是一种常用的方法。通过对周围基站的监控，获取目标UE与基站的交互信息，通过截取基站下发的对目标UE的调度信息，可以在相应的时频资源上接收目标UE的信号。对于全球移动通信系统（Global System For Mobile Communications，GSM）来说比较简单，基站给UE分配频点和时隙,对应的在该频点和时隙接收UE上行信号即可。对宽带码分多址（Wideband Code Division Multiple Access，WCDMA）及LTE来说，因为采用了正交编码，很多时候，时频资源上多个UE是共存的，但是通过某种介入操作总能在某些时频上获取到单独目标UE的上行信号。而且，空间谱估计可以同时估计多个目标方位，即使信号同频相关也能区分出来。这正是采用空间谱估计测量DOA的优势。

图3所示为一组LTE终端随机接入信号在接收阵列上的仿真数据，假设阵元具有一致性，则每一个阵元接收到的数据根据阵元所处阵列的位置有一定相位差，利用各阵元接收数据之间的相关性进行空间谱估计，可以得到信号到达方位角。

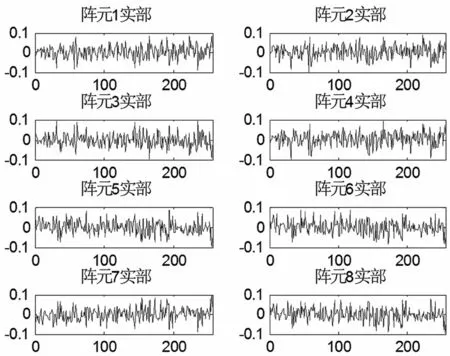
图3 LTE终端随机接入阵元接收数据

2.2 DOA估计

图4 所示为采用1.2节式（8）的空间谱估计 函数。

图4 随机接入信号的空间谱估计

接收信号为2.1节中两个UE的上行随机接入仿真信号，水平方位角分别为13°和20°，可以看到，在相应方位上形成了两个尖锐的谱峰。由此可以看出，空间谱估计用于信号DOA估计非常有效。而且，通过分析，在信号个数小于阵元数，信噪比较大时，方位分辨角可以精确到1度，增加阵元数量能进一步提高角度分辨率。同时，增加阵元间隔可以抵消部分信噪比降低的精度损失，但是，当阵元间隔增加到一定程度后，会出现假峰。LTE的随机接入信号带宽达到1M,对于GSM这种窄带信号，或者用LTE中上行参考信号[4]来做空间谱估计会有更好的效果。

2.3 AOA定位

传统对UE的AOA定位需要至少两个基站，每个基站通过测量同一个UE的信号DOA，再通过定位服务器解算出UE位置。本文的AOA定位与传统对UE的AOA定位最大的区别就是无需基站参与，完全依靠空口监听实现无感定位。上一节的空间谱估计测量了信号方位角，这对于定位UE来说还是不够的，只要通过移动测量设备多次测量，通过多次估计的DOA，辅以三角几何运算，就可以实现AOA定位。AOA定位的精度取决于DOA估计的精度和设备本身移动距离的测量精度。

图5所示为基于空间谱估计的AOA定位示意图。粗实线箭头表示行进路线的三条道路，箭头方向为天线阵列的0°方向；细实线箭头表示估计出的DOA方向；一共测量了三个点，每个点测量十次取平均值。细实线箭头交点的圆圈表示对UE的精确定位。这里对数据做了一定的过滤，在十次样本数据中去掉了偏离平均值较大的数据。

图5 AOA定位示意图

3 结 语

基于空间谱估计的UE精确定位属于一种AOA定位，该方法基于非合作接收技术，无需基站参与，通过监听基站下行信号对目标UE的调度信息，在相应目标时频位置接收目标上行信号。采用经典MUSIC算法，用接收天线阵列的接收样本数据估计出信号向量空间和噪声向量空间，进一步得到空间谱估计。结合多次不同位置的测量可以获得DOA交点即是UE的精确定位。该AOA定位的精度取决于空间谱估计的DOA精度，而空间谱估计的精度取决于阵列的设计及UE上行信号的质量。因为公网的特性，不用基站参与的UE上行信号的获取始终是困难的，因为其他用户的干扰以及信号的多径传输都给上行信号的接收带来现实困难。所以，基于UE上行信号的空间谱估计AOA精确定位作用距离都有限，在运用该方式精确定位之前需要首先知道目标UE所处的服务小区，这个通过运营商后台数据或者其他小区定位设备很容易获得先验信息，因此该方法在公共安全领域还是具有很大的应 用价值。