一种伪卫星网络双天线双频定位算法*

吴千爽，邓 平

（西南交通大学 信息科学与技术学院，四川 成都610000）

0 引 言

近几十年，全球卫星导航系统（Global Navigation Satellite System，GNSS）应用非常广泛。对于高楼密集区的地区和位于深山峡谷中的水库大坝等，由于卫星信号受到遮挡，接收机观测到的卫星数较少，卫星几何图形分布不佳，导致卫星定位精度大大降低。此外，应用卫星定位技术进行精密测量，目前在水平方向的定位精度可达到毫米级；但在垂直方向，卫星定位精度较差，难以满足高精度测量的要求。伪卫星定位技术成为一条解决上述卫星导航和定位现存问题的有效途径。

伪卫星即陆基卫星，是指布设在地面上的类似于卫星的导航定位收发设备。伪卫星不仅可以增强卫星导航信号，同时也能实现独立组网定位[1-2]。通过四颗或者四颗以上伪卫星收发机可以组成一个独立的定位网络，为该区域内的接收机提供高精度位置服务，如图1所示。与单颗伪卫星或者多颗非组网伪卫星相比，此伪卫星网络中各个收发机之间通过时间同步技术，实现严格的时间同步。直接消除了接收机直接的时钟误差，使定位更加准确。

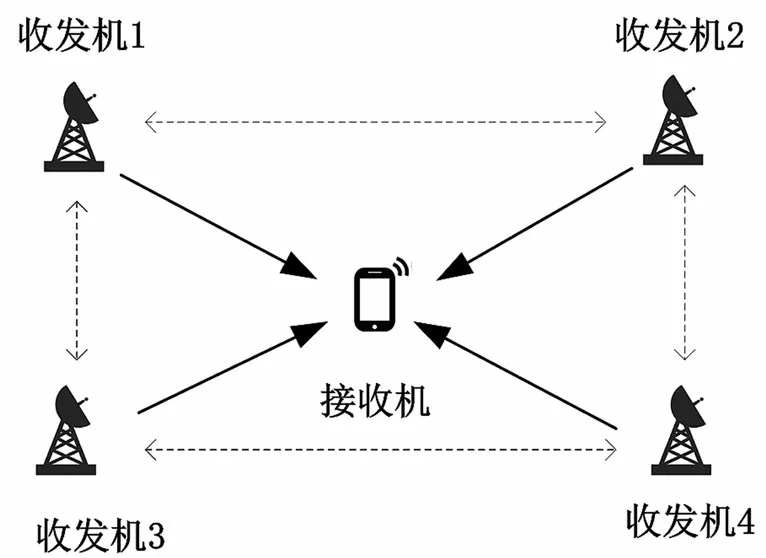
图1 伪卫星网络示意图

在伪卫星网络定位算法中，整周模糊度的解算是实现快速、高精度定位的基础。从1981年Counselman[3]提出基于载波相位观测量进行高精度定位以来，国内外学者一直在研究整周模糊度的解算问题，先后提出了多种整周模糊度解算方法。其中，Cellmer S[4]基于模糊度函数法提出了一种新的载波相位数据处理算法，该算法无需经过整数搜索就能得到模糊度的整数解，此算法减少了计算时间，但在精度上有所欠缺。Li Xin[5]在传统的模糊度函数法基础之上，提出了改进的粒子群优化算法，实现了室内伪卫星的厘米级定位。Wei jiang[6]等人提出了一种基于几何变换的扩展卡尔曼滤波算法来解算整周模糊度，该算法利用单差载波相位测量来实现精确定位，较传统的已知点初始化法（Known Point Initialization，KPI）在精度和效率上都有所提高。文献[7]中针对传统确定模糊度搜索空间的方法较为保守，致使搜索空间过大这一问题，提出了一种基于最小二乘模糊度降相关平差法（LAMBDA）的改进方法。文献[8]利用北斗卫星导航系统双频载波相位观测值组成宽巷双差观测值,运用LAMBDA算法，实现了宽巷双差整周模糊度的解算。Bertsch J[9]等人针对locata系统提出了一种在航（On The Fly，OTF） 的模糊度解算方法，在模拟的测量中，定位精度达到了厘米乃至毫米级别。

本文提出了一种模糊度的双天线双频解算方法。该算法首先在伪卫星定位网络收发机双天线设计的基础上得到双频单差载波相位观测方程；其次将观测方程线性化，利用加权最小二乘算法得到整周模糊度的浮点解；再通过LAMBDA算法得到模糊度整数解，并进一步得到接收机的准确坐标。

1 伪卫星单差双频观测方程

参照整周模糊度的单频解算过程，其双频的载波相位观测方程为：

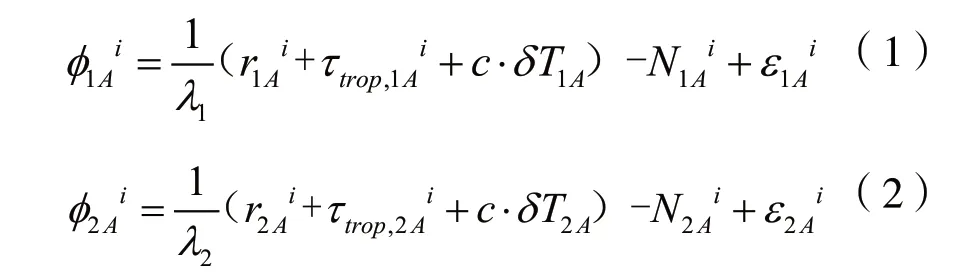
为了消除接收机钟差，减小系统偏差，构造双频单差载波向量观测方程：

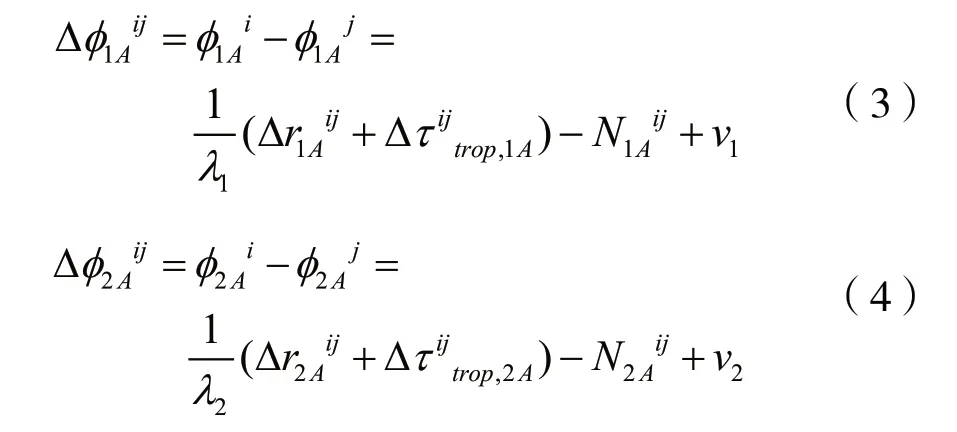
上式中，

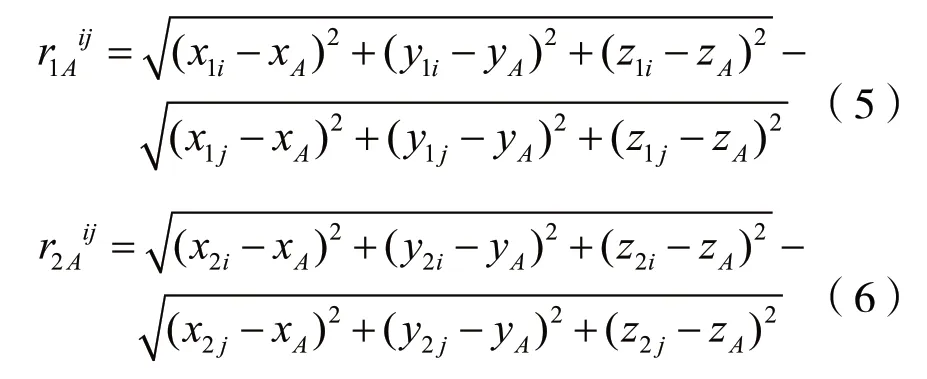
其中，(x1i,y1i,z1i)、(x2i,y2i,z2i)分别为收发机i天线1和天线2的坐标，(x1j,y1j,z1j)、(x2j,y2j,z2j)分别为收发机j天线1和天线2的坐标，式中的未知量为接收机A的位置坐标(xA,yA,zA)和双频单差整周模糊度

2 整周模糊度解算

若建立的地面伪卫星网络有m+1个收发机，接收机在n个历元进行观测，可得到(n+2m)×1维单差观测向量z：

以及(3n·2m)×1维未知向量x：

把向量x分为两部分，位置坐标和整周模糊 度，即：

将多个历元的单差双频载波相位观测方程组利用泰勒级数展开：

其中，Δz为观测值增量，Δxc为坐标信息初始值的增量，ΔxN为单差整周模糊度增量，Acc和ANN分别为整周模糊度和位置坐标的雅克比矩阵。

雅克比行列式Acc表达式如下：

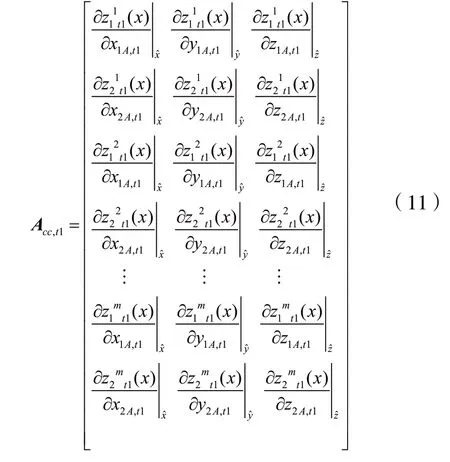
由上述一个历元的表达式，可推导出n个观测历元的雅克比矩阵：

某一个历元的整周模糊度的雅克比矩阵为：

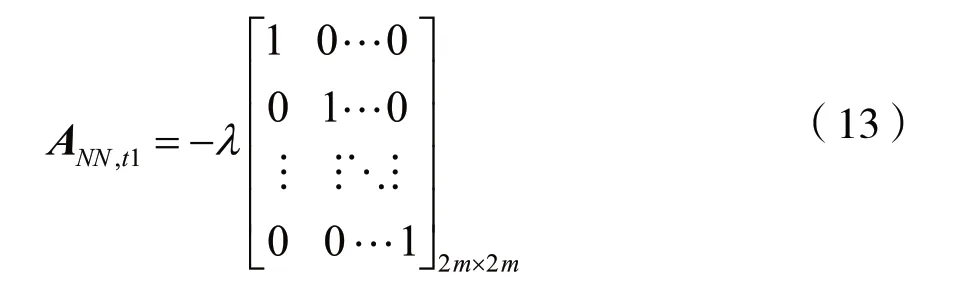
则n个历元整周模糊度雅克比矩阵：

不同频率的单差测量值不相关，而同一历元，同一频率的单差测量值，因为有相同的参考量，所以是相关的[10]，因此，一个历元的误差协方差阵表述成下列式（15）：

则n个历元误差协方差阵为：

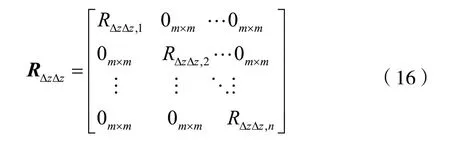
利用加权最小二乘算法[11]得到整周模糊度的浮点解为：

其中N0=[ANNACC]，权矩阵

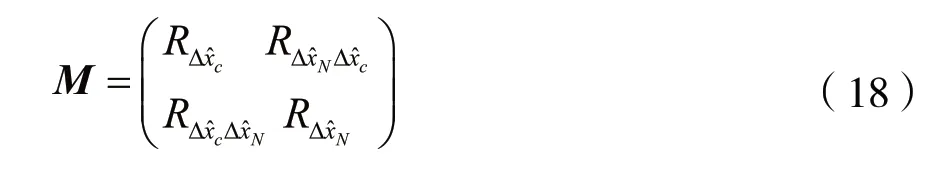
在模糊度浮点解和其协方差矩阵都已知的情况下，运用LAMBDA算法得到其整数解，LAMBDA算法原理如下[12]：

整周模糊度的求解问题可以转化为下式：

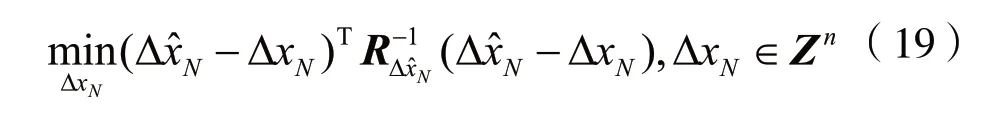
由于未知数有整数限制，只能通过搜索的方式得到解。搜索表达式如下：

单差观测向量之间存在相同的参考量，具有较强的相关性，使得搜索困难。LAMBDA算法通过整数变换，使得搜索空间压缩，在体积不变的情况下，将椭球体变成近似球体，使得搜索容易进行。

整数变换即Z变换后的变量和协方差矩阵如下：

由此，式（19）变为下式（24）的最小化问题：

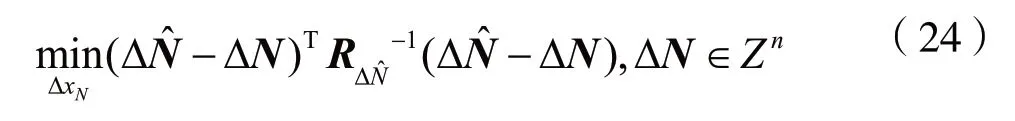
整数变换后，与式（21）相对应的搜索空间为：

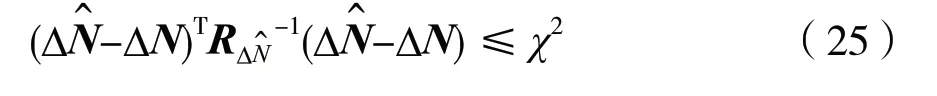
3 仿真分析

本文仿真场景的建立参照文献[9]，布局了五颗伪卫星网络试验场景，每颗伪卫星的收发机均含有两根天线，分别发射两个频率信号，天线坐标如表1所示。开始阶段，采用了接收机运动轨迹上的十个历元的载波相位观测数据通过仿真得到表2的结果。单差载波相位观察误差为N（0，0.04）cm。

表2中，搜索的单差模糊度整数解由LAMBDA算法得到。本文仿真建立的五颗伪卫星网络场景，在双天线发射两个频率的情况下，有8个整周模糊度。浮点解最小的偏差为0.04周，最大的偏差为0.67周。

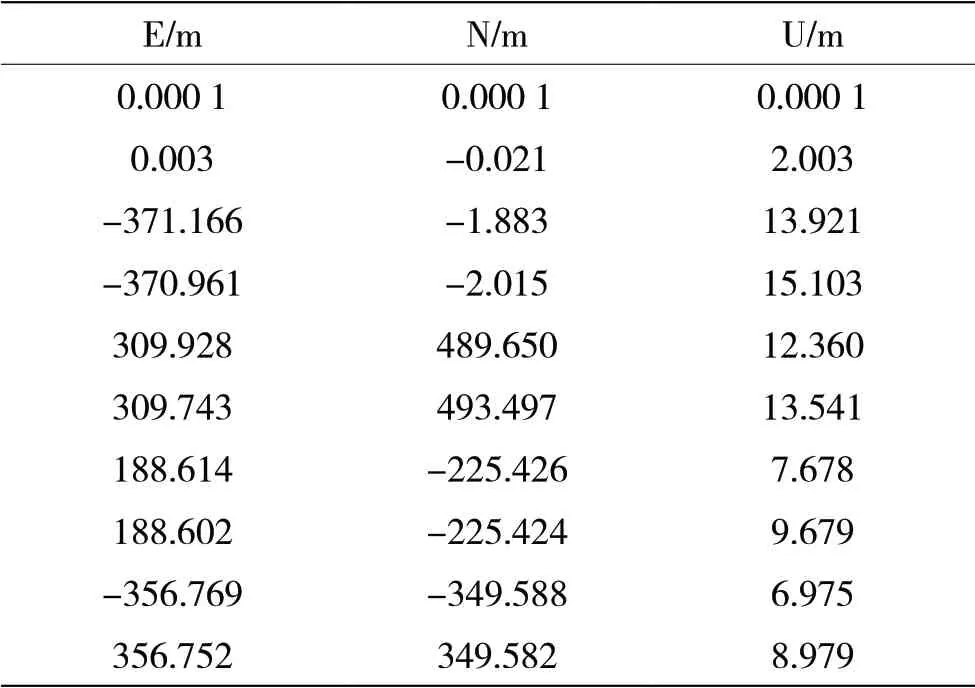
表1 伪卫星坐标

表2 整周模糊度解算结果

上述仿真计算得到的双频单差整周模糊度作为双频算法的初始解；单频仿真使用了每颗伪卫星的一根天线，发射同一频率，并采用了正则化优化准则[13]。假设接收机坐标为（-20，10，0），单差载波相位观测误差为N（0，0.04）cm。单点定位1 000次。 图2、图3给出了双频与单频单点定位结果。

图2 双频定位结果

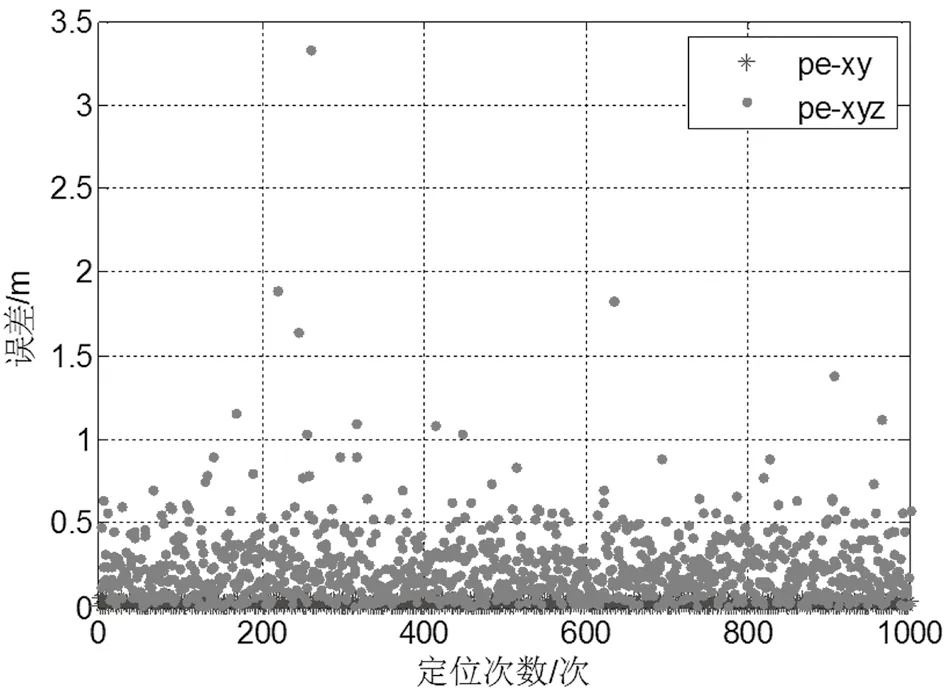
图3 单频定位结果

比较图2、图3可以看出，无论是三维还是二维，双频的定位精度比单频的定位精度高。双频定位误差比较集中，都在0.5 m以下，单频定位结果相对要发散一些。同时，无论是单频定位误差还是双频定位误差，二维定位精度由于只统计水平方向上的误差，所以始终优于三维定位精度。

图4、图5给出了本文算法与文献[10]中算法对比结果。横轴为误差，纵轴为在此误差以内的点所占的百分比。从图4中可以看出，1 000次仿真实验中，本文双频定位结果二维误差在0.02 m的达到了92%左右，而单频定位误差在0.02 m的仅有60%。图5中，双频定位误差几乎全部都在0.4 m以下，而单频定位误差在0.4m以下的只有82%。图4与图5中虚线为文献[10]算法结果，从二维统计误差来看，本文单频算法比文献[10]的算法略微提高了一点定位精度，但是在三维统计误差中，本文的单频算法由于使用了正则化优化准则，所以对定位精度有比较明显的提升。

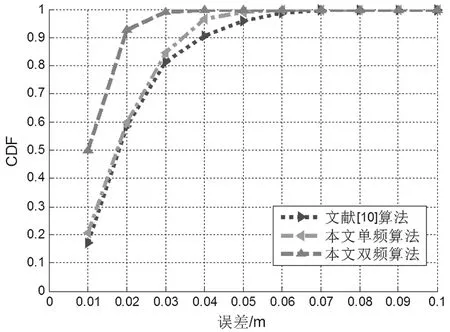
图4 二维误差统计

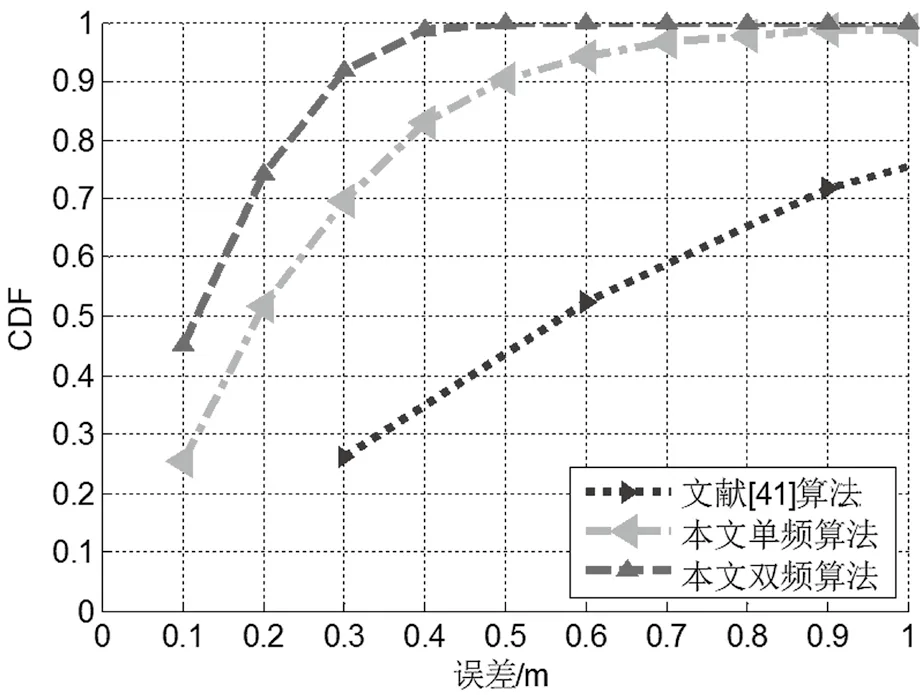
图5 三维误差统计

为了更加详细的比较伪卫星网络中单频与双频定位算法的性能，突出双频定位算法的优越性，在上述的仿真条件下，使接收机从起始点（30，30，0）按照抛物线运动，运动方程如式（26），运动时间为100 s。图6、图7、图8分别为3个方向上的误差比较。

图6 E方向误差比较

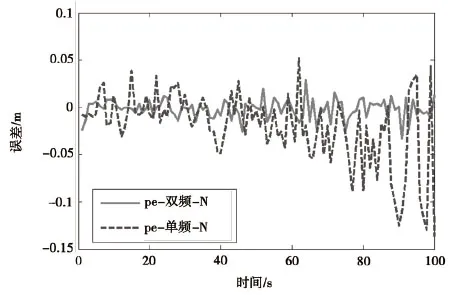
图7 N方向误差比较

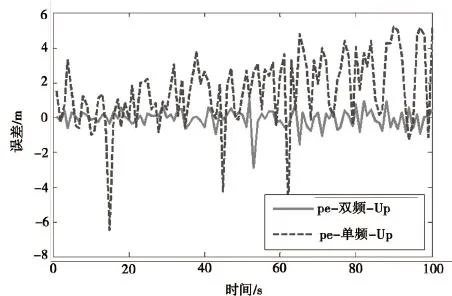
图8 U方向误差比较

图6 、图7、图8中实线为双频定位误差，虚线为单频定位误差。可以看到，无论是单频还是双频，在E方向的定位误差最小，在U方向上的定位误差最大。这是因为伪卫星的位置，导致E方向的精度因子较小，U方向的精度因子比较大。上述三图中，单频定位误差在仿真时间内均比双频定位误差大，在图7中，随着接收机的运动，虚线波动变大，而实线没有明显的波动变化，而且在某些位置上，可以看到虚线的波动很大，而实线较虚线波动小很多。这说明双频定位算法有更好的定位性能。

精度因子的大小体现了伪卫星网络布局的好坏，也一定程度上反映出定位精度。图9、图10给出了接收机在100 s的运动内，水平方向精度因 子（Horizontal Dilution of Precision，HDOP）和垂直方向精度因子（Vertical Dilution of Precision，VDOP）。从图中看出，收发机采用双天线发射不同频率，显著减小了精度因子值。在伪卫星网络中，各收发机位置相同的情况下，采用双天线设计，这不仅是增加一倍的载波相位观测方程，而且对于接收机来说，两根天线相当于两个收发机，这改善了伪卫星的几何布局，定位精度也随之提高。

图9 水平方向精度因子

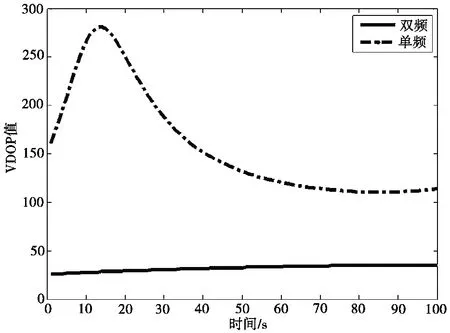
图10 垂直方向精度因子

对两种定位方式的误差进行统计分析，得到 表3。

表3 误差统计

两种方式定位误差的均值和标准差如表3所示。可以看出，采用双频载波相位观测算法对定位精度有相当明显的提升，在E和N方向上分别提升了0.54 cm和2.3 cm。而在U方向上即垂直误差提升了1.67 m。因此伪卫星采用双天线发射两个频率信号能够提升伪卫星组网定位精度，特别是垂直定位准确度。

4 结 语

本文针对伪卫星网络定位系统，基于接收机双天线设计基础上提出了双频在航定位算法。根据双天线发出的不同频率的信号，接收机同时观测得到双频载波相位观测方程，运用加权最小二乘算法得到模糊度浮点解，再通过LAMBDA算法搜索出模糊度整数解，最后得到接收机的准确位置。当伪卫星布局不理想，几何精度因子很大，单天线发射单频信号，容易造成定位误差过大，甚至不能定位的情况，而双天线发射双频信号恰恰能够改善这一点。通过仿真实验结果显示，该算法明显提高了定位精度，特别是在U方向上。本文主要考虑了在双天线的情况下，每一根天线发射一个频率，未来还将进一步对每根天线发射两个频率以及天线位置对定位的影响进行研究。