基于改进遗传算法的移动机器人路径规划

陈亮 陈君若

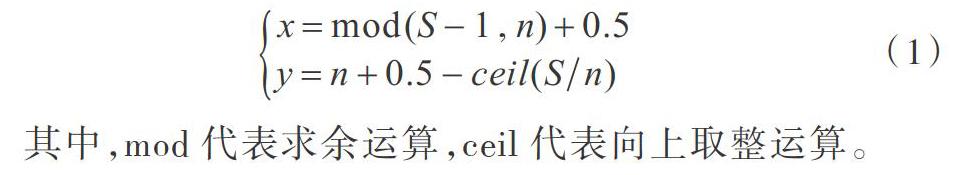
摘 要：经典遗传算法的缺陷在于搜索耗时较长，容易出现局部最优解。为解决该问题，引进适应度函数，并在设计遗传算子时，重新定义适应度函数。为尽量规避出现局部最优解，在不改变种群参数的条件下，通过新算法得到最短路径为31，搜索耗时均值为20.667m/s;与之对比，经典遗传算法两项数据分别是37和24.667m/s。因此，新算法可在更短时间内给出更佳解。

关键词：遗传算法;移动机器人;路径规划;交叉算子;变异算子

DOI：10. 11907/rjdk. 191190

中图分类号：TP301文献标识码：A文章编号：1672-7800（2019）004-0024-04

0 引言

目前机器人智能化发展迅速，在工业、科学探索、国防军事等重要领域应用广泛。移动机器人是深度智能和人类智慧融合的产物，也是机械控制、传感器、仿生学、信号处理等若干学科交叉发展的结果[1-4]。当前，移动机器人主要应用难题之一是路径规划，即如何使机器人在避开各种障碍的前提下，以最优路径从出发点移动到目标点。通常情况下，移动机器人工作环境较为复杂，首先需确定任务，然后机器人按照各方面环境信息（由操作者提供或通过传感器采集）作出决策，最终执行任务。大部分路径规划研究均应用了多种优化算法，如人工势场法、蚁群优化算法、神经网络和遗传算法等[5-10]，本文综合应用优化栅格法及回归预测法探讨在静态、动态障碍环境下移动机器人路径规划。

为弥补传统栅格法的缺陷，本文以障碍物为单位采集信息，有效缩小信息存储空间。通过新势场函数与沿墙跟踪算法，解决障碍物目标不可达和陷阱区等多个问题;再采取量子粒子群算法确定人工势场参数以弥补传统栅格法的缺陷，从而实现更优的路径规划;最后探讨机器人振荡问题，对算法进行针对性优化[11-16]。

针对遗传算法在路径规划方面的缺陷，如容易出现局部最优解、收敛耗时长、优化结果不够稳定等，学者们不断对其优化，但大部分学者通过随机方法得到初始种群，该方法无法有效提高路径质量，导致收敛耗时延长，甚至出现过早收敛。因此，本文从优化适应度函数着手，提高进化效率，降低出现早熟收敛的可能性。实验结果显示，利用优化自适应遗传算法可显著提升路径规划质量。

2 基于改进遗传算法的路径规划方法

2.1 路径编码

按照由左到右、由上到下的顺序，将栅格从1-400进行编号，1号、400号栅格分别是机器人移动起点和终点。利用MATLAB完成栅格模型序号编码（见图1）。

2.2 种群初始化

2.2.1 栅格路径选择

由于本研究中机器人周围环境已知，所以障碍物信息（数量、位置）均可确定，在环境模型栅格化时，自由栅格、障碍物栅格的区分十分简单。为提高初始化准确性、节省初始化时间，笔者利用先验知识，确保路径以目标点为方向进行初始化，并在自由栅格中选定路径。如此路径不会经过障碍物，但无法确保路径可不间断地抵达目标点，因此本文采用不连续自由栅格路径，即在起点和终点之间，随机选择自由栅格为路径节点，尽管选出的栅格难以完全连续地连接起点和终点，但可使算法更加灵活。

2.2.2 算子插入

在路径非连续位置，通过附近的自由栅格予以填补，从而得到不经过障碍物的连续路径，此即为插入算子。通过式（2）分析相邻两个栅格是否连续。

若计算得出[pi]序号栅格属于自由式栅格，则仅需填补插入。非自由栅格以最近自由栅格插入，若该操作无法实现，则证明该个体是不可行路径，算子被淘汰。反复执行上述步骤，直至某个体变为连续可行路径或被淘汰。如果是种群初始化形成的非连续自由栅格路径，通过插入算子予以修补使之连续，此时种群初始化成功。先验知识的应用使初始化的个体均属于可行路径，无需应用惩罚函数，可大幅减少运算工作量和算法耗时。

2.3 适应度函数

该函数为最小化目标函数，定义适应度函数为：

2.4 遗传操作

2.4.1 算子选择

算子选择的作用是为了实现在群体规模恒定下，删除较弱适应度的个体，以免群体内较强适应度个体遭到淘汰，然后对未被删除的个体予以交叉、变异处理，由此得到下一代个体。在选择环节，笔者综合应用轮盘赌法及精英保留策略，以确保机器人适应度目标的实现。

2.4.2 交叉操作

交叉环节内，彼此配对的两个个体交换部分基因，进而获得两个新个体。生物进化过程十分繁琐，其中最重要的是染色体重组、变异。所以，遗传算法最重要的步骤为交叉环节，其赋予了算法极强的搜索能力。以二进制编码为例，目前应用最广泛的交叉方法有如下3种[17-20]：

（1）单点交叉。交叉的两个个体编码串内，随机选择某交叉点进行交叉，则它们的点前或点后部分会产生两个新个体。用X1、X2代表待交叉的两个个体，则有：

随机位置选择5，通过单点交叉得到新个体 Y1、Y2。

（2）两点交叉。上一种交叉方式仅需采用一个交叉点，其需用到两个交叉点，然后交换两者结构，用X1、X2代表待交叉的两个个体，则有：

随机位置选择3、7，完成交叉操作后得到個体 Y1、Y2。

（3）一致交叉。采用该交叉方式时，需要设定屏蔽字，从而确定两个父代个体含有的特定基因可延续至下一代。当屏蔽字为0时，父代X1基因将遗传予子代个体Y1;在屏蔽字为1时，父代个体X2基因将遗传予子代个体Y1，由此得到子代个体Y1，否则得到子代个体Y2，例如：

2.4.3 变异操作

变异的本质是用基因取代染色体中的某些基因，从而得到全新的染色体。该环节旨在确保种群具有充分的多样性，同时降低出现早熟收敛问题的可能性。以二进制编码串为例，目前应用最广泛的变异操作包含[21-22]：

（1）基本变异。基于变异概率，个体染色体编码串内随机挑选一个或更多基因展开变异，其详细操作如下：

在3和6这两个位置发生变异，此时可得新个体Y1。

（2）逆转变异。逆转变异也属于基本变异范畴。通过随机方法，在染色体编码串内挑选两个点进行逆转，基于逆转概率对两点基因值展开反向排序。以二进制编码串为例，其逆转变异过程如下：

于3、7两个位置产生逆转变异，此时可得到个体Y1。

（3）自适应变异。该方式的变异概率可基于种群多样性灵活改变。通常情况下，其与交叉环节得到的子代个体海明距离呈线性负相关关系。

2.5 遗传算法流程

遗传算法流程如图2所示。

3 实验结果与分析

3.1 实验结果

为了解算法改良后的效果，在[20×20]的栅格环境模型中对算法展开仿真分析，然后与经典遗传算法进行对比。在应用经典遗传算法时，随机产生初始种群，通过轮盘赌法确定算子，算法参数包括：种群规模[M=50]，交叉概率[pc=0.8]，变异概率[pm=0.1]，最大进化代数[T=100]。实验结果见图3-图5，对该图进行分析可以确定该算法提供的路径比经典算法更短。

3.2 算法对比分析

在实验中保持控制参数不变，如种群规模、交叉或变异概率、遗传代数上限值等。实验结果表明，优化后的算法能够在更短的时间内得到全局最优解，在收敛时不会出现局部最优解。两种算法在路径规划时间、最短路径长度方面的对比详见表1。对表中数据进行分析可知，优化后的算法能够在更短的时间内给出规划路径，且路径长度比经典算法更短。

4 结语

经典遗传算法收敛耗时长、容易出现局部最优解等缺陷极大限制了其在移动机器人路径规划领域的应用。为此，本文对适应度函数进行重新定义，从而有效优化了遗传算法，使算法能够在更短时间内完成进化。在栅格环境中展开实验以了解优化后的算法表现。结果发现，经过优化后的遗传算法在移动机器人路径规划方面具有更大的实用性。但是本文遗传算法时效性与准确性有待提高，下一步研究可采用鲸鱼优化算法提高遗传算法算子的优良性，降低搜索范围，大幅降低传统遗传算法工作量，尽量规避局部最优解出现的可能性。

参考文献：

[1] 孙绍华，王魁生，张恬恬. 基于Mirosot平台改进遗传算法避障策略[J]. 中北大学学报：自然科学版，2019（1）：70-73+78.

[2] 牟玲龙，柴永生，殷守民，等. 一种多关节机器人几何标定方法研究[J]. 机电工程技术，2019（1）：16-20+142.

[3] 刘宁宁，陈志军，闫学勤. 基于IAFSA和AGA混合算法的移动机器人路径规划[J]. 现代电子技术，2019（3）：157-162.

[4] 裴以建，杨亮亮，杨超杰. 基于一种混合遗传算法的移动机器人路径规划[J]. 现代电子技术，2019，42（2）：183-186.

[5] 温贻芳，孙立宁，徐朋. 表面改性冗余机器人关节空间的轨迹优化算法[J]. 机械科学与技术，2018，37（12）：1870-1874.

[6] 陈尔奎，吴梅花. 基于改进遗传算法和改进人工势场法的复杂环境下移动机器人路径规划[J]. 科学技术与工程，2018，18（33）：79-85.

[7] 趙蕊，许建，王淼，等. 基于遗传算法和分数阶技术的水下机器人航向控制[J]. 中国舰船研究，2018，13（6）：87-93.

[8] 薛阳，张晓宇，江天博，等. 基于视觉导航的巡检机器人双模控制研究[J]. 控制工程，2018，25（11）：1982-1987.

[9] 侯庆隆，杨冬，郭士杰. 工业机器人能耗优化方法研究综述[J]. 计算机工程与应用，2018，54（22）：1-9.

[10] 杨帅，邹智慧. 积分滑模水下机器人导航定位控制方法仿真[J]. 计算机仿真，2018，35（11）：306-309+365.

[11] 于振中，李强，樊启高. 智能仿生算法在移动机器人路径规划优化中的应用综述[J/OL]. 计算机应用研究：1-13.2018-11-05. http：//www.arocmag.com/article/02-2019-11-086.html.

[12] 吴瑞芳，孙兆丹. 采用粒子群算法耦合遗传算法优化双臂机器人模糊逻辑控制研究[J]. 组合机床与自动化加工技术，2018（10）：40-43.

[13] 陈庆胜. 基于改进遗传算法的机器人轨迹跟踪[J]. 智能机器人，2018（5）：58-61.

[14] 陈尔奎，吴梅花，张英杰. 复杂环境下煤矿救灾机器人路径规划[J]. 煤炭技术，2018，37（10）：301-304.

[15] 林晓青，杨继之，乐毅，等. 一种可移动检测机器人站位规划策略[J]. 宇航学报，2018，39（9）：1031-1038.

[16] 张毅，刘芳君，胡磊. 结合MPGA-RBFNN的一般机器人逆运动学求解[J]. 智能系统学报，2019（1）：165-170.

[17] 曹凯，高佳佳，高嵩，等. 移动机器人在复杂环境中的在线路径规划[J]. 自动化与仪表，2018，33（9）：27-31+62.

[18] 李房云，赵巍，邓文鹏. 基于行为进化的智能保洁机器人设计与仿真[J]. 计算机产品与流通，2018（9）：128.

[19] 梁凯，陈志军，闫学勤. 移动机器人路径规划仿真研究[J]. 现代电子技术，2018，41（17）：167-172.

[20] 翁祖昊. 遗传算法在自动机器人拣货路径选择中的应用研究[J]. 自动化应用，2018（8）：91-92.

[21] 侯仰强，王天琪，岳建锋，等. 基于多目标遗传算法的双机器人协调焊接路径规划[J]. 中国机械工程，2018，29（16）：1984-1989.

[22] 贾超广，肖海霞，胡广新. 基于改进遗传算法的包装机器人轨迹规划[J]. 包装工程，2018，39（15）：183-187.

（责任编辑：江 艳）