基于子带能量分析的数字接收机数据语音段识别方法研究

黄均安 詹毅

摘 要：在无线电侦听领域，侦听数据中常常含有纯噪音、误判为语音的定频数字调制信号等非语音信号段，造成侦听人员工作效率下降。针对该问题，提出一种基于子带能量分析的语音段识别算法。考虑到侦听数据在时域上存在幅度跳变现象，首先利用直方图分析对侦听数据进行分段，得到若干个子数据段，然后对每个子数据段进行子带能量分析，最后提取特征参数实现对语音段的识别。仿真结果表明，该方法能够准确地对侦听数据进行分段，并识别出其中的语音段。

关键词：纯噪音;定频数字调制信号;子带能量;语音段识别;无线电侦听

DOI：10. 11907/rjdk. 181707

中图分类号：TP319文献标识码：A文章编号：1672-7800（2019）001-0162-04

Abstract： The intercepted data contains pure noise， frequency-fixed with erroneous judgement of speech as well as others non-speech signal sections in the field of radio interception. Hence， it causes a decline in staff's efficiency. Aiming at this problem， a speech recognition algorithm based on the sub-band energy analysis is proposed. In view of the fact that a phenomenon of intercepted data that exists range hop on the time domain. Firstly， the histogram analysis is made to get sub-data segments. Secondly， each sub-data segment is analyzed by means of sub-band energy analysis. Finally， to pick up the characteristic parameter is to achieve recognition of speech signal segments. As the simulation result shows that the method can not only section interception data with much accuracy， but also recognize speech segments.

0 引言

信息在当今社会中扮演着重要角色，电磁频谱作为信息的载体，对电磁频谱的监测与侦听是军事及民用领域获取信息的一种重要手段。民用领域对电磁波的监测与侦听有利于开展安防工作，军事领域对电磁波的监测与侦听是收集情报的一种重要手段，可为有关部门提供决策参考。侦听接收机在电磁频谱的监测与侦听中起着关键作用。电磁频谱的监测与侦听对象具有频段宽、信号种类多、通信环境复杂、先验知识少等特点[1]。基于传统结构的侦听接收机体积庞大、处理能力有限、可重构能力差，无法满足当前侦听工作的需求。软件无线电[2-3]技术具有多种类、可同时获取多频段数据等特点，符合侦听接收机的技术要求。软件无线电的基本思想是以一个通用、标准、模块化的硬件平台为依托，通过软件编程实现无线电台的各种功能[3]。因此，目前国内多采用此类侦听接收机对电磁频谱进行监测与侦听。由侦听接收机采集的数据经过人工复听便可完成信息收集工作。由于侦听接收机的特点，通过软件无线电侦察接收机采集的侦听数据中通常存在纯噪音[4]，以及误判为语音的定频数字调制信号等大量非语音信号，严重影响了侦听人员工作效率。

因此，为了提高人员工作效率，需剔除侦听数据中所有的纯噪音段与定频数字调制信号段。单独使用任何一种调制识别方法都无法很好地识别所有调制方式，因此采用多级调制识别系统[5-7]是十分必要的。在多级调制识别中，第一级识别只需对调制信号进行粗略划分，第二级识别再对调制信号进行详细划分。对于第一级调制方式识别，一般是将信号分为模拟调制信号与数字调制信号。目前针对模拟与数字调制方式的识别，多采用码元速率估计方法[8-10]。其基本理论依据是：模拟调制信号没有码元速率，其估计结果为任意无规律值，而数字调制信号有码元速率，其估计结果为一定值。参考文献[8]提出基于包络平方谱的模拟与数字调制方式自动识别算法，该算法计算简单，对数字调制信号的滚降系数不敏感;参考文献[11]通过对零中频信号进行非线性处理，得到含有符号速率的离散谱线，再利用四阶累积量方法在抑制高斯背景噪声的同时，提取符号速率的基频分量。该算法运算简单，适应性强;参考文献[12]提出采用非线性变换与小波变换相结合的方法估计码元速率，无需设置判决门限即可实现模拟与数字调制方式的分类，但上述算法识别对象均为相位信息完整的信号。目前针对纯噪音的研究相对较少，针对信号与AWGN（Additive White Gaussian Noise）区分的研究较多，其基本理论依据是：AWGN频谱包络是平坦的，但信号谱表现不同，有明显的共振峰[13]。参考文献[13]提出AWGN因子用于信号与AWGN的区分，但该算法对于非AWGN的纯噪音并不适用。本文针对上述问题，提出一种基于子带能量分析的语音段识别方法。仿真结果表明，该算法能够在识别对象相位信息不完整的情况下，实现语音段与纯噪音段、定频数字调制信号段的分离。

1 算法描述

1.1 整体算法描述

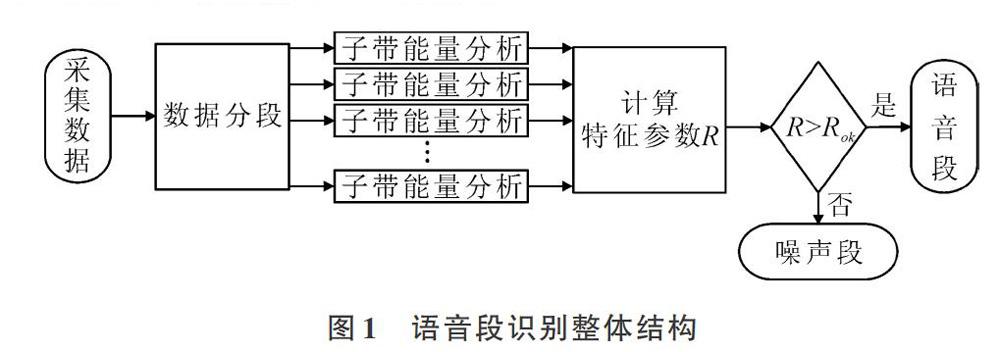
算法框图如图1所示，包括数据分段、子带能量分析，以及语音段、纯噪音段与定频数字调制信号段识别3个阶段。通过直方图分析算法对输入的采集数據进行幅度分段，得到若干不同幅度等级的子数据段，对每个子数据段进行子带能量分析并计算特征参数，并将特征参数与统计观察得到的阈值进行比较，从而实现语音段、纯噪音段及定频数字调制信号段的分离。

1.2 数据分段

侦听数据中存在幅度跳变现象，根据帕斯瓦尔定理[14]，幅值大小会影响子带能量分布。为了降低幅值对子带能量分布的影响，首先对侦听数据按照幅度等级进行分段，得到子数据段。直方图是展示连续分布最常用的工具，其本质上是对密度函数的一种估计[15]。通过对语音信号统计特性的研究表明，对于语音信号振幅分布概率密度有两种逼近方法，一种是修正伽玛分布概率密度函数，另一种是拉普拉斯分布概率密度函数[16]。根据长期统计来看，用拉普拉斯分布描述语音信号统计特性的精确性低于采用伽玛分布进行描述，但其函数式更加简单，也可采用高斯分布（Gaussian）进行近似描述[16]。以上3种概率密度函数均为单峰分布，而存在幅度跳变的侦听数据振幅直方图呈多峰分布，且幅度跳变处出现在振幅直方图的谷点处。因此，需选择合适的统计量对侦听数据进行直方图统计，若呈单峰分布，则该侦听数据中不存在幅度跳变;若呈多峰分布，则该侦听数据中存在幅度跳变，然后提取直方图分布中的极小值点作为分段阈值实现幅度分段。本文选择局部幅度绝对值作为统计量进行直方图统计，局部幅度绝对值的最大值为最大次序统计量[17]，可以对语音信号幅度分布进行有效简化，并突出幅度跳变特性，具体表示为：

对局部极小值点进行模糊处理，可得到作为幅度分段阈值的局部极小值点。局部极小值仅表明幅度跳变可能分布在其中，由于实际信号局部极小值情况的复杂性，仅以局部极小值为门限作为检测幅度跳变与幅度分段的依据，常常会出现两类错误：一类是错误检测幅度跳变，即实际没有幅度跳变，但误判为存在幅度跳变。研究发现，对于实际的正常语音信号，尽管没有幅度跳变，但直方图中仍然存在局部极小值，比例不小于某一门限，所以可以设置一个合理门限，以避免此类错误;另一类是存在幅度跳变，但选取幅度跳变的门限不准确，也即是说，以直方图分布的局部极小值作为门限，会造成幅度跳变检测结果不准确。研究发现，在此类情况下局部极小值的附近值都很接近，以局部极小值对应的幅值作為门限并不能真实反映实际情况，通过对局部极小值附近直方图作进一步估计，可以有效改善上述问题。

1.3 子带能量分析

由于语音信号段、纯噪音段以及定频数字调制信号段相互之间存在幅度差异，因此分段得到的每个子数据段的属性具有唯一性，可以通过子带能量分析对每个子数据段属性进行判断。纯噪音段与定频数字调制信号段的频谱能量在一段时间内是平坦的，而语音信号段含有共振峰频率，其频谱能量在一段时间内是非平坦的，起伏较大，所以将子数据段分帧后，求取该子数据段中每帧数据的能量。选择的滤波器组为Mel-scale滤波器组，Mel倒谱系数由于很好地描述了人耳的听觉感知特性，因而取得了较其它特征参数更好的识别效果，是目前最常用的特征参数[18]，可以表示为：

1.4 算法实现

（1）对子数段进行分帧处理。设一个子数据段为[s（n）]，分帧后得到帧信号段[si（n）]，语音信号为时变信号，频谱随时间不断变化，但在短时间内（1帧，时间长度为20～40ms）可以认为频谱是不变的，故帧长选择20～40ms，帧移为帧长的0～1/2。本文侦听数据的采样率为64kHz，帧长选择32ms（0.032*64 000=2 048样本点），帧移为16ms（1 024样本点）。

（2）计算每帧信号的能量并归一化。计算每帧信号的离散傅立叶变换（DFT），可以表示为：

1.5 特征参数提取

得到子数据段每帧信号的子带能量后，可以通过提取特征参数，实现语音段、纯噪音段及定频数字调制信号段的分离。语音信号含有共振峰频率，相邻帧同一子带间的能量变化较大，而纯噪音与定频数字调制信号相邻帧同一子带间的能量变化很小。特征参数R定义为5个子带能量方差的极差，如式（7）所示。

2 算法仿真与分析

为了验证算法性能，本文利用MATLAB进行仿真，仿真数据来源于某单位的侦听数据。图2、图3分别展示了存在幅度跳变现象与无幅度跳变现象数据的时域图及统计量的[yabsmax（n0）]直方图。其中，若侦听数据中存在幅度跳变现象，则在时域图中用黑色方框标识出幅度跳变段。由图2可以看出，侦听数据时域图中存在明显的幅度跳变现象，其统计量[yabsmax（n0）]的直方图分布整体呈多峰形状，且分布中存在明显的局部极小值点。因此，局部极小值点即为幅度分段的阈值。故在极小值处即为幅度跳变点的情况下，本文提出的基于直方图分析的数据分段算法可以准确标记出侦听数据中的幅度跳变段。由图3可以看出，侦听数据的时域图中不存在幅度跳变现象，其统计量[yabsmax（n0）]的直方图分布整体呈单峰形状，但存在局部极小值点，若直接将局部极小值作为分段阈值进行处理，则会造成错误分段。本文通过1.2节提出的方法对局部极小值进行模糊处理，有效解决了该问题。

图4、图5分别是语音信号与纯噪音的时域图及对应的子带能量分布图。在子带能量分布图中，横轴为侦听数据分帧后帧信号的编号，纵轴为每帧信号5个梅尔刻度的子带能量，颜色明暗代表子带能量大小，颜色越亮代表子带能量越大。图4为语音信号时域图及对应的子带能量分布图，可以看出，由于语音信号中共振峰的存在，不同帧同一子带的能量变化很大，图中显示每行的颜色变化无固定规律，颜色明暗随机分布;图5为一段纯噪音的时域图及对应的子带能量分布图，可以看出，由于纯噪音与定频数字调制信号频谱包络是平坦的，故子带能量分布图中每行的颜色变化存在一定规律，颜色明暗要么基本保持不变，要么逐渐变亮或变暗。图5属于每一行颜色逐渐变亮的类型，这是由于时域中数据振幅与时间呈正比关系，根据帕斯瓦尔定理，则频域中数据功率与频率也呈正比关系。高斯白噪声则属于每一行颜色基本保持不变的类型。

图6展示了59个语音段、69个纯噪音段或定频数字调制信号段特征参数R的分布情况。其中颜色较浅的点代表语音信号段，颜色较深的点代表纯噪音段及定频数字调制信号段。可以看出，语音信号特征参数R的数值与纯噪音及定频数字调制信号特征参数R的数值在分布上存在明显的聚类现象。通过观察特征参数R的分布寻找合适的阈值，可以实现语音信号段、纯噪音段及定频数字调制信号段的分离。本文设置阈值为4.5（图6中黑色直线所示）。

3 结语

本文在相位信息未知的情况下，提出一种基于子带能量分析的语音段识别方法。该方法首先利用直方图分析对存在幅度跳变的侦听数据进行幅度分段，得到子数据段，然后对每个子数据段进行子带能量分析，最后提取子带能量特征参数实现对语音段的识别。该方法可以扩展到对任意几个频谱分布存在差异信号的分离。仿真结果表明，本文算法简单、可靠，可以有效去除侦听数据中的非语音信号段，大大提高了侦听人员的工作效率。

参考文献：

[1] 许军， 汪芙平， 王赞基. 基于软件无线电的数字侦听接收机研究[J]. 电子技术应用， 2007（8）： 110-112.

[2] 杨小牛，樓才义， 徐建良. 软件无线电原理与应用[M]. 北京： 电子工业出版社，2002.

[3] 吴丹，顾学迈，吴芝路. 基于软件无线电的数字化接收机的研究[J]. 电子技术应用， 2005（9）： 50-52.

[4] 彭设强， 潘浩，周瑞. 侦听系统中纯噪音辨析模块的设计与实现[J]. 软件导刊，2009，8（11）： 96-97.

[5] 戴威，王有政，王京. 基于AR模型的调制盲识别方法[J]. 电子学报，2001（S1）：1890-1892.

[6] NANDI A K， AZZOUZ E E. Algorithms for automatic recognition of communication signals[J]. Biulleten Eksperimentalno？ Biologii I Meditsiny， 1998， 37（7）： 23-35.

[7] HSUE S Z， SOLIMAN S S. Automatic modulation classification using zero crossing[J]. Radar & Signal Processing IEEE Proceedings， 1990， 137（6）： 459-464.

[8] 包锡锐， 吴瑛. 基于谱特征的模拟与数字调制方式识别方法[J]. 计算机工程与设计， 2008（14）： 3569-3571，3576.

[9] TAIRA S， MURAKAMI E. Automatic classification of analogue modulation signals by statistical parameters[J]. IEEE Signal Processing Magazine，1999（1）： 202-207.

[10] 姚亚峰，陈建文，黄载禄. 模拟与数字调制方式的非线性变换识别方法[J]. 电讯技术，2005（1）： 23-26.

[11] 张海瑛，袁超伟. 采用非线性变换的MPSK/MQAM符号速率盲估计[J]. 电子科技大学学报， 2010， 39（6）： 820-825.

[12] 王兰勋，张瑞华. 模拟与数字调制信号的识别方法[J]. 通信技术，2008（3）： 46-48.

[13] 杨志俊， 范海波， 曹志刚. 基于谱分析的通信信号调制方式自动识别[J]. 无线通信技术， 2003（2）： 30-33.

[14] 赵道利， 梁武科， 罗兴锜， 等. 水电机组振动信号的子带能量特征提取方法研究[J]. 水力发电学报， 2004（6）： 116-119，115.

[15] 谢益辉. 现代统计图形[EB/OL]. https：//yihui.name/cn/publication/.

[16] 赵力. 语音信号处理[M].第3版.北京： 机械工业出版社， 2016.

[17] 茆诗松. 高等数理统计[M]. 北京： 北京大学出版社， 2007.

[18] 项要杰， 杨俊安， 李晋徽， 等. 一种适用于说话人识别的改进Mel滤波器[J]. 计算机工程， 2013， 39（11）： 214-217，222.

[19] 梁红波， 司景萍， 高志鹰， 等. 基于子带能量法的发动机振动信号分析研究[J]. 噪声与振动控制， 2010， 30（1）： 72-77.

[20] 田野， 王作英， 陆大. 基于子带能量线性映射的噪声中端点检测算法[J]. 清华大学学报：自然科学版， 2002（7）： 953-956.

（责任编辑：黄 健）