梯次利用锂离子电池健康状态估计
(北京信息科技大学、北京电动车辆协同创新中心 北京 100192)
通常来讲,动力电池的平均使用年限大约为5-8年,其性能随着使用时间的增长而逐渐衰退,当电池的当前容量衰减至额定容量的80%是,将不再适用于电动汽车,必须从原来的电动车退役。而这些退役电池的容量大多数在初始容量的60%-80%,如果直接报废,将造成资源的巨大浪费。根据预测,到2020年我国新能源汽车退役动力电池累计将达25GWh。如此规模的退役动力电池,如果不能妥善处置,势必将对生态环境造成新一轮的污染,也将影响到我国新能源汽车及动力电池产业的健康发展。因此,开展电池梯次利用,有利于资源的合理利用,这就涉及到退役电池的筛选,准确的估计退役电池的健康状态是电池筛选的必要步骤。
采用了Thevenin等效电路模型,基于HPPC实验对该等效电路模型进行了参数辨识,并通过Matlab-simulink建立了电池的等效电路模型并进行了模型的验证。进行电池的SOH估计之前,首先采用拓展卡尔曼滤波对电池的SOC进行估计,接下来采用双拓展卡尔曼滤波对电池的SOC和SOH进行同时估计并通过仿真对该算法进行了验证。
一、电池模型的建立
(一)电池模型的选择
Thevenin等效电路模型如图所示,锂电池的开路电压等效为Uoc,Ro为锂电池的欧姆内阻。Rs表示电池的极化内阻,Cs表示的是电池的极化电容,他们组成电池的一阶RC并联回路,以此来代表电池在极化过程中的压降[1]。

图1 戴维南等效电路模型
(二)电池等效电路模型的建立
首先,利用Matlab的Simulink模块搭建电池的等效电路模型。图2是电池的Simulink等效电路模型。

图2 电池等效电路模型
(三)模型的参数辨识
针对戴维南模型,Ro,Rs,Cs等参数未知,可以通过实验进行识别。对于此,采用HPPC实验法进行参数的识别。HPPC(混合脉冲功率特性试验,Hybrid Pulse Power Characteristic)采用脉冲电流来测试电池的动态功率特性。对于等效电路模型的相关参数,可利用HPPC的实验结果进行识别[2]。室温下进行HPPC实验,如下:
1.实验设备。实验对象为8块锰酸锂退役电池,以及电池充放电测试设备。
2.实验前的预处理,首先对电池进行预处理循环:①以0.2C恒流充电至截止电压4.3V,接下来进行恒压充电至电流为0.02C为止。②静置1小时。③以0.2C放电至放电截止电压3V。④静置1小时。⑤重复步骤①-④五次。⑥以最后三次所测得电池容量的平均值为电池的实际容量。
3.根据FreedomCar混合动力汽车电池测试手册中的HPPC实验,实验步骤。如下:①测试前,以0.2C的电流恒流将电池充至充电截止电压4.3V,接下来以恒压充至电流减小至0.02C为止;此时电池充满,此过程即为CCCV的充电过程。②搁置1小时,使电池处于平衡状态。③用1C电流放电10s,搁置40s后再用0.75C的电流充电10s,用1C电流是SOC减少10%,静置1小时。④重复步骤③,当SOC=10%时停止实验[3]。
HPPC实验的全程电流示意图如图3所示。

4.节点的参数识别。结合电池戴维南模型原理以及电池放电过程中的电压特性可对每个节点参数进行识别。首先选取节点为SOC=90%的电流和电压示意图,如图4所示。
通过观察图4可以总结得到,整个HPPC实验包括两个阶段,充电和放电。两个阶段较为相似。所以在此仅研究U1至U5的放电阶段。也就是研究U1-U2,U2-U3,U3-U4,U4-U5。
式中τ=TpCs为时间常数



到此,该节点的参数识别完毕;其他节点的参数识别同理可得[5]。依据HPPC实验数据可计算得到各项参数。
二、模型的验证
接下来进行模型的验证,通过对比模型的计算电压以及实际测量所得的电压,来验证模型的精确度。模拟HPPC实验的一段,将得到的仿真数据和实验所得的数据进行对比。
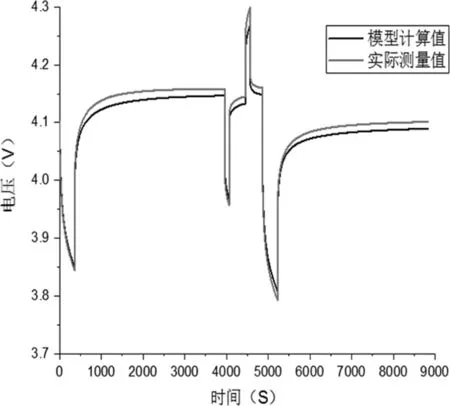
图5 数据对比图
从图5中可以看出,模型测量值与实际测量值图像的走势大致相同。模型测量值和实际测量值绝对误差不超过40mv,因此,戴维南等效电路模型准确度满足要求。可以看出,戴维南模型可以满足模拟电池工作的要求。而且,通过实验辨识的参数可信度满足要求[4]。
三、双拓展卡尔曼滤波估计电池的健康状态
(一)基于拓展卡尔曼滤波的电池的SOC估计
由电池的等效模型的状态方程可得,要准确估计电池的SOH,其前提是准确的估计电池的SOC。因为电池的SOC属于非线性变化,所以在此采用EKF(拓展卡尔曼滤波)对电池的SOC进行估计。下式为系统的状态方程以及测量方程[5]:yk=g(xk,uk)+vky(k+1)=f(xk,uk)+wk
依据戴维娜等效电路模型得出的电池SOC的估计的矩阵方程是:
f=(xk,uk)=Ak-1xk-1+Bk-1uk-1
g(xk,uk)=Uoc,k+Ub(k)+i(k)Ra(k)
(二)基于双拓展卡尔曼滤波的电池的SOH的估计

图6 双拓展卡尔曼滤波工作原理
图6为双拓展卡尔曼滤波的工作原理,所谓双扩展卡尔曼滤波实际上就是两个拓展卡尔曼滤波同时工作(即EKF1和EKF2)。这之中,EKF1进行状态估计,EKF2进行参数估计。在这两个滤波器之中都具有状态更新以及量测新。
在本节,采用双拓展卡尔曼滤波,电池健康状态及荷电状态被同时估计。估计SOC的拓展卡尔曼滤波器是电池的参数估计。剩下的一个滤波器被用来估计电池当前时间的额定容量。最后,利用电池的容量的定义公式来计算电池当前时间的健康状态[6]。
本节采用的DEKF详细的过程在此列出:
首先,电池当前时间的实际可用容量,在此假设为一个缓变参数,依据前文电池健康状态(SOH)和荷电状态(SOC)估计过程之中建立的方程,并且在本文建立的等效电路模型的基础之上,可以得到以下的双拓展卡尔曼滤波的估计模型:
xk+1=akxk+Bkuk+wkCk+1=Ck+rk
yk=Uoc,k+Ub(k)+i(k)×Ra(k)+vk=g(xk,uk)+vk
依据上式知道,双拓展卡尔曼滤波的基础上,电池健康状态(SOH)的估计是和电池荷电状态(SOC)的估计是同时进行的。即在估计电池的SOC同时,也估计了一次电池的当前时间实际最大可用容量。
DEKF的具体过程是:
1.当K=0时,进行初始化

2.时间更新过程
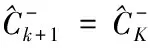

3.测量更新过程

(三)算法的验证与分析
以上是基于双拓展卡尔曼滤波算法进行估计得到SOH,为了验证其准确性,接下来进行仿真,以此来分析对比。在仿真的过程中首先设置电流激励曲线,该曲线应在0.3C、0.4C、0.5C三种电流倍率之中随机生成,以此来对应验证前文进行的退役电池所进行的容量测试实验。在此设置电池的初始容量为30.56Ah,SOC的值是95%,仿真所进行的时间是1200s.图7为仿真所得到估计曲线和实验所得到的真实测量值曲线的对比。
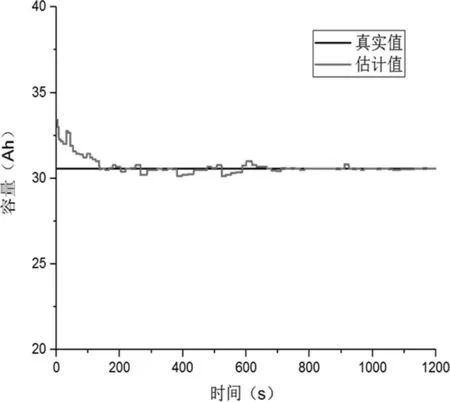
图7 拓展卡尔曼滤波估计值与容量真实值对比
在图7中可以看出,在仿真进行的初始时段,估计值和测量值存在一些偏差。但是在经历了一段时间的波动之后,拓展卡尔曼滤波算法的估计值较迅速的收敛于真实的容量值附近。并且随着时间的增加,由于卡尔曼增益的作用,使得仿真误差越来越小并且逐渐维持在较小的误差范围之内。仿真对比结果表明,双拓展卡尔曼滤波算法具有很好的优势,精度高,具有很好的鲁棒性。
四、总结
本章首先对几种常见的电池模型进行了分析,综合各自的优缺点,最终采用了计算简单,准确度较高的戴维南等效电路模型。在选择好电池模型之后,进行了等效电路模型的参数辨识,基于HPPC实验,对该电路的参数尽行了辨识。随后进行了参数的验证实验。接下来简单介绍了卡尔曼滤波以及拓展卡尔曼滤波,在此基础上建立了SOC和SOH的估计模型。最后采用DEKF算法估计了电池的SOH。并进行了仿真实验,以此来验证算法以及模型的准确度。

