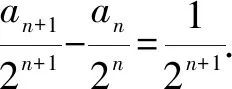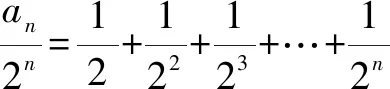强化审题教学 提高解题能力
黄旭明
(福建省福安市第三中学 355002)
2017年版普通高中数学课程标准提出了数学学科核心素养与课程目标的新理念.随着新课改的施行,高中数学教学中更加重视学生分析和解决问题能力的培养.而正确解题的前提是全面准确地审题,仔细审题是正确理解题意,找出题目条件,明确解题目标的关键所在.只有对所给出的题目有了整体和准确的认识,并对题目进行科学合理的推断分析,才能掌握解题方向,构建起正确的解题途径.
一、斟字酌句 准确理解
逐字逐句地读题分析是审题的重要步骤,细心关注题目中的关键词,如“至少”,“不小于”,“恰有一个”等.只有领悟了其确切含意,才能找到解题的突破口,叩开解题之门.
案例1 已知集合M={(x,y)|y=k,k∈R},N={(x,y)}|y=ax,a>0,a≠1,x∈R},若M∩N只有一个子集,则k的取值范围是( ).
A.k<0 B.k≤0 C.k>0 D.k≥0
解题分析许多学生画出两个函数略图,却错选了C.究其原因是没有认真读题,把“只有一个子集”误以为两个图象只有一个交点.实际上,M∩N只有一个子集,也就是有M∩N=∅,即直线y=k与曲线y=ax没有交点.由两个图象的位置关系可知k≤0.故本题正确选项应是B.
二、抓住关键 正确辨析
对于一些形似的题目,其区别往往是关键的词或字.若没注意关键词字,往往容易混淆,导致错误.因此应引导学生仔细读题,抓住关键词字,辨析不同词字的本质区别,准确理解题意,实现正确解题.
案例2 (1)已知函数y=log2(x2-ax+a)的定义域是R,求实数a的取值范围;
(2)已知函数y=log2(x2-ax+a)的值域是R,求实数a的取值范围.
解题分析在课堂上,我让两个学生到前面在黑板上分别板演解答两个题目.结果两个同学都是列出了式子Δ=a2-4a<0,得到0 两个不同的题目为什么得到相同的结果?这引起班级同学的疑惑.我发动班级同学展开讨论,许多同学发表了自己的不同见解.通过争论,最终全班同学明白了,解题的关键是对“定义域是R”与“值域是R”这两个词的准确理解.(1)题是要求“恒有x2-ax+a>0”;而(2)题是要求“x2-ax+a应取到一切正数”.因此,(1)题应列Δ<0;而(2)题应列Δ≥0. 人们在数学解题时,往往习惯于传统的思维方式着手分析求解.但按这种常规的思路有时却陷入困境,或由于解题过程麻烦难以实施,或理不出思维头绪无法入手.此时不妨重新审题,对题目的条件、目标从不同的角度深入解读,从中挖掘出隐含的信息,来增强题设条件,减少思维障碍,简化问题求解. 案例3 设函数f(x)=(a-3)x3+9x,若函数f(x)在区间[1,2]上的最大值是4,求a的值. 解题分析在函数、导数、不等式综合复习课上,针对此题,我与学生共同探讨了解题思路.为求f(x)的最大值,先求导,f′(x)=3(a-3)x2+9.由于f′(x)=0不一定有解,需要对a-3的符号分类讨论;接着还要根据f′(x)=0的根与区间[1,2]的关系,再一次进行分类讨论.学生普遍感到这道题太复杂了,不易求解.我引导学生再次读题,抓住条件“f(x)在区间[1,2]上的最大值是4”深入挖掘,用特殊的f(1)≤4,f(2)≤4来缩小a的取值范围,进而明晰了f′(x)的符号,知道了f(x)的单调性,得到了f(x)的最大值.这样就回避了复杂的分类讨论. 由此知f′(x)=3(a-3)x2+9在区间[1,2]上是递减的,所以f′(x)max=f′(1)=3a<0,所以f(x)在区间[1,2]上是减函数. 所以f(x)max=f(1)=a+6=4,得a=-2. 从本例可以体会到,有些问题用常规方法难以求解时,应回头重新审视题目,仔细研读题目条件,深入挖掘题目中隐含的信息.这样常会有新的发现,改善题目条件,降低题目难度,从而获得顺畅的解题思路. 对于一些陌生的题目,在审题时,应多方联想,积极思考,善于将陌生的问题转化为自己比较熟悉的和容易解决的问题. 案例4 已知数列{an}满足a1=1,an+1=2an+1,求数列{an}的通项公式. 解题分析在数列复习课上,展示出该题后,发动学生寻找解题思路.五分钟后,一些学生纷纷给出了解题思路. 生A:我一时想不出怎样求解,但依次求出前几项是1,3,7,15,31,63,….它比熟悉的等比数列2,4,8,16,32,64,…的每一项都小1,因此我猜想通项公式应该是an=2n-1.为了严密,应该用数学归纳法加以证明,我还没证完. 生B:我想到了探索等差数列等比数列时所用的方法,用后一式减前一式. 将an+2=2an+1+1与an+1=2an+1相减,得到an+2-an+1=2(an+1-an). 可见差数列{an+1-an}是公比为2的等比数列.而它的首项是a2-a1=2,这样,可整体求出an+1-an=2×2n-1=2n.再把an+1=2an+1代入,求出an=2n-1. 生C:我也是想到了运用等差数列等比数列的方法. 将an+1=2an+1两边同除以2n+1, 联想到差式恒等式 bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1) 得an=1+2+22+…+2n-1=2n-1. 生D:我是想到能否找到一个数x,使递推式化为an+1+x=2(an+x),这样能转化为等比数列. 将该式展开整理后是an+1=2an+x.再与原来的递推式an+1=2an+1对照,知x=1.因此有an+1+1=2(an+1).可见新数列{an+1}是公比为2的等比数列,它的首项是a1+1=2.所以an+1=2×2n-1,得an=2n-1. 多种解题思路的展示交流,引起了学生们的极大兴趣,开阔了学生们的思维,提升了学生们运用数列知识方法的能力.为延续学生们的兴趣,我又提供了三道思考题,供学生们课后探究. 1.已知a1=1,an+1=2an+n-1,求通项an. 2.已知a1=1,an+1=2an+2n+1,求通项an. 3.已知a1=1,an+1=2an+3n,求通项an. 总之,提升学生的解题能力是一个多方面的系统工程,需要长期的训练培养,积累总结.但在具体解题时,首要的还是审题.通过审题,明确题意,广泛联想,发现思路.然后入手,设计思路,操作实施,实现目标.因此,在解题教学中,如何有效地提升学生的解题能力,以致提升学生的数学素养,是我们高中数学教师应该探讨的实际问题.三、挖掘隐含 简化问题
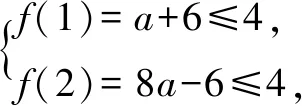
四、广泛联想 善于转化