海港口浮码头中固定桩墩振动实测与数值计算分析
丁俊凯 李强 臧传海

【摘 要】 为更好地研究港口浮码头中桥台墩的位移响应、动力响应特性和振动产生的原因,采用非线性有限元分析软件Abaqus进行二维数值仿真模拟,并比较实测位移数据得到理论位移曲线。最后与现场工程固定桩墩结构的实测位移曲线进行拟合对比分析,显示模拟结果与实际工程状况符合较好,表明钢引桥的推动力和波浪的动力作用是造成桩墩振动的主要原因,对解决相关工程结构施工安全问题具有实际意义。
【关键词】 固定桩墩;钢引桥;波浪力;动力响应
0 引 言
港口浮码头是由浮趸船、固定桩墩、钢引桥、锚链和一些支撑体系构成的建筑物。
船舶在靠离码头时,船体会对浮码头承台桩体产生碰撞、挤压和摩擦,加上近海波浪力、风力环境的共同作用,对浮码头稳定性的要求也越来越高。浮码头运营过程中的受力因素较为复杂,需要建立物理模型进行研究。本文基于有限元软件建立扩展D-P本构关系二维模型模拟浮码头中固定桩墩,研究浮码头桩―土相互作用、结构耦合振动、信号处理和动力响应分析等方面内容。
本文基于MATLAB编程处理振动加速度信号,结合某码头工程,对实际工程中存在的浮码头振动问题进行现场测试与分析,认为在复杂环境条件下引起浮码头固定桩墩振动的原因是浮趸船在波浪、风等自然条件作用下造成的钢引桥振动和波浪力直接作用于固定桩墩而引起的结构振动。为验证这一假设,测试了结构和钢引桥振动,根据测试结果分析了结构的双自由度方向振动位移变化,使用Abaqus数值模拟建立了二维桩墩模型,计算得出数据曲线(桩墩的位移振动曲线),并与现场测试数据曲线进行对比。测试结果验证了这一假设。
1 码头工程概况与现场测试
1.1 码头工程概况
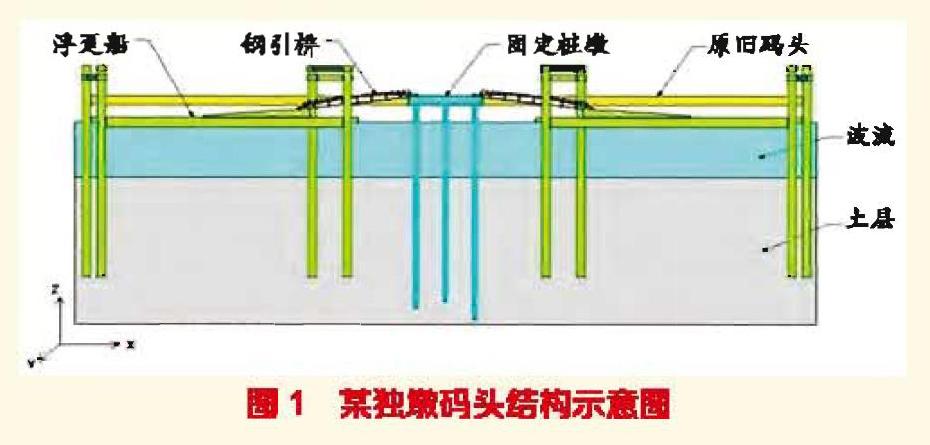
某海港码头扩建工程是在旧固定桩墩外侧新修建一段桥台墩(见图1,x轴为顺岸水平方向,y轴为垂岸水平方向,z轴为竖直方向)。桥台墩在顺岸两边与钢引桥通过两个部件直接连接,浮趸船与钢引桥之间有钢吊架和钢梁,用侧桩柱和锚链固定浮趸船。桥台墩尺寸为14 m 1.8 m,由9根(3)的直径为0.8 m的管桩组成,桩与桩距离为5 m。钢引桥使用21 m m的钢管倾斜放置,斜率是1︰7。单座钢引桥质量约19.28 t。
1.2 现场测试
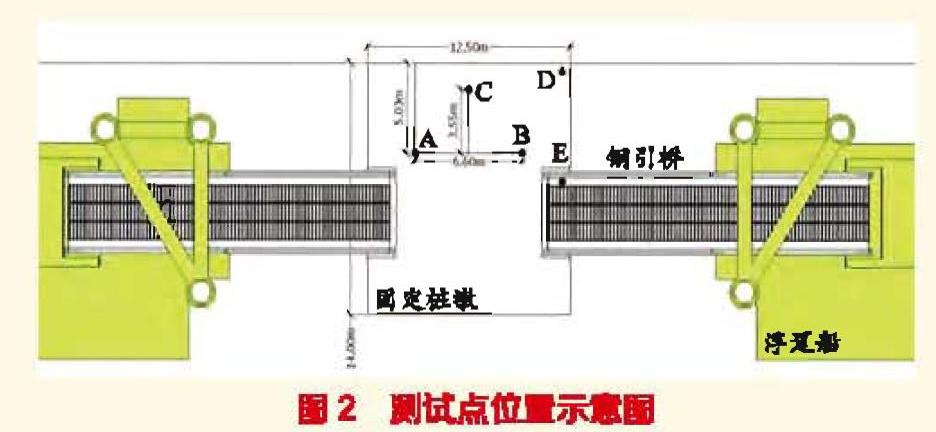
现场测试使用KD1100LC仪器测量,分为3组。测试点位置见图2,分别为A、B、C,B、C、D,D、E等3组测试点,前两组测试点在固定桩墩上,第三组测试点则在固定桩墩和钢引桥上。所有的测试点均测量竖直、顺岸、垂岸等3个方向的数值。
1.3 测试数据与分析
使用MATLAB软件编写频率积分程序,绘制竖直、顺岸、垂岸等3个自由度方向实测位移曲线,分析经频域积分处理的固定桩墩竖直方向、垂岸方向及顺岸方向的实测位移曲线和钢引桥竖直方向、垂岸方向及顺岸方向的实测位移曲线,得出以下结论:
(1)固定桩墩竖直方向最大位移约为0.8 mm,垂岸方向最大位移为2 mm,顺岸方向最大位移为8 mm。
(2)钢引桥竖直方向最大位移约2 mm,垂岸方向最大位移为10 mm,顺岸方向最大位移为10 mm。
(3)无论哪个方向,钢引桥的振动幅度都要大于固定桩墩的振动幅度。钢引桥和固定桩墩在顺岸和垂岸两个水平方向的位移都比竖直方向大得多,与实测情况基本吻合。
2 浮码头中固定桩墩有限元分析
2.1 平台模型
浮码头固定桩墩由桥台墩、管桩和土体组成(见图3)。
图3中,E点、F点为桥台墩与钢引桥的接触点,钢引桥对固定桩墩的作用由钢引桥自身的重力和钢引桥振动力共同引起。分别在E点、F点施加同向竖直方向力f1、f3,逆向水平方向施加力f2、f4。若m为钢桥对点E、F点施加的自身质量,a为模拟数据加速度或者现场实测数据加速度,则f=ma。
2.2 简化模型的刚度等效
使用二维模型进行计算,会因为维度原因产生误差,因此要将二维模型和三维模型在水平方向上的刚度进行等效。
2.3 实测与模拟结果
由于模型只对水平方向进行等效,没有对竖直方向进行等效,因此只对水平方向模拟效果进行分析,而不考虑竖直方向数据。
2.3.1 模拟信号计算结果
在图3 E点、F点处加集中力,得到模拟信号加速度曲线。通过数学物理方法,考察E点、F点相位变化,计算两点之间的相位差,从而模拟现场的振动时间差。假设E点、F点初始时间t0为0.10 s、0.20 s、0.30 s、0.40 s、0.50 s、0.60 s,将这两点的曲线导入软件进行计算,得出两点在水平方向位移的结果,见图4、图5:
由圖4和图5可知,E点和F点两点在水平方向上初始时间(相位差)变大,竖直方向的位移值也在不断变化。当t0为0.2 s时,相位差达到最大值,即振幅最大,相位差的描述可以简化为在E、F两点水平方向加同方向和同大小的作用力f,即f2=f4,这时在水平方向达到振幅的峰值;当t0为0.4 s时,相位差最小,即振幅最小,相位差的描述可以简化为在E、F两点水平方向加反方向同大小的作用力f,即f2=-f4,这时在水平方向上达到振幅的谷值。振幅的数值在两个相位差之间变化,存在极值。由图3、图4可以发现振动幅值周期与水平和竖直加速度信号的施加有一定的关系。
2.3.2 实测信号计算与横向稳定性分析
实际工程中的振幅受到多种因素影响,情况较为复杂。可以先考虑模拟单一波浪力作用因素下E点、F点的二维模型水平方向位移,见图6。在以上数据基础上,经过处理,提取钢引桥测试点同一10 s时段内的加速度数据(见图7),相当于在两点施加集中力,将现场实测数据导入数值模拟软件。考虑承台两边加速度相位变化因素,用同向和反向加速度模拟现实中相位差变化引起的振动幅值变化。
E点和F点在水平方向上的加速度为a2、a4,竖直方向上的加速度为a1、a3。E点、F点的同向加速度在水平和竖直方向上的加速度一致,水平方向相反即a2=-a4,竖直方向相同即a1=a3,结果见图8,可见其振动波形与波浪力作用下的振型相同,说明E点、F点的水平集中荷载处于同向加速度的情况下会互相抵消,耦合振动为最小值。
E点、F点的反向加速度在水平方向上相同即f2=f4,在竖直方向上相反即f1=-f3,结果见图9;E点、F点振动波形与图7情形相比,变化较大,说明E点、F点的水平集中荷载处于反向加速度的情况下振动更加明显,耦合振动为最大值。
结合图8、图9,模拟固定桩墩的二维模型的振动,得到的最大振幅范围为 6~6 mm。固定桩墩顺岸方向实测位移信号见图10,位移信号曲线比较接近反向加速度的模拟曲线。从图10可知,由钢引桥的推动力所引起的位移变化大约是由波浪力引起的位移变化的10倍,可以得出现实中钢引桥对固定桩墩造成的作用明显大于波浪力对固定桩墩造成的作用的结论。
2.4 结 论
通过对固定桩墩实测位移和二维模拟位移进行拟合对比分析,可以得出以下结论:
二维模拟固定桩墩位移在水平方向上的模拟结果与实测结果较为接近,而在竖直方向的模拟结果比实测结果小,原因是二维模型在竖直方向没有对进行刚度等效。
本文所做的有限元模型分析中,固定樁墩的振动主要由两个因素引起,钢引桥的振动作用和波浪力的推动作用。其中钢引桥的振动是桩墩振动的主要原因,模拟计算结果与实测振动信号基本一致,符合实际情况。
波浪对港口浮码头建筑物的作用是波浪力、风力等自然因素与固定桩墩、钢引桥、浮趸船等结构共同互动作用的结果,需要通过建立物理、几何模型进行分析研究。通过对某港口浮码头设计方案的振动作用的物理、几何模拟,表明当处于极端天气下,波浪对港口浮码头的推动作用更加明显,对于港口浮码头固定桩墩的设计和施工提出了更高的要求。
3 结 语
本文研究了港口浮码头在复杂环境下波浪力作用下钢引桥共振和固定桩墩自振的耦合振动问题,并建立二维数值模型对桥台墩的刚度数据等效处理后利用有限元法进行二维数值模拟分析,将实测加速度信号频域积分位移数值结果,与数值模拟位移数值结果进行拟合对比,分析影响浮码头结构中固定桩墩的双自由度振动的因素,得出以下结论:港口浮码头中固定桩墩的振动的主要因素是钢引桥的推动力和波浪的动力作用。

