汽车空调一维物理模型开发及应用

张磊，宫晓彬，钱锐



汽车空调一维物理模型开发及应用

张磊，宫晓彬，钱锐

（泛亚汽车技术中心有限公司，上海 201210）

为了完成汽车空调最大制冷性能、最大加热性能的预测，基于热、流网络节点、能量平衡的理论，使用AMEsim建立制冷系统物理模型，使用Simulink建立空调箱、乘客舱物理模型，通过跨平台联合仿真，完成空调最大制冷性能、最大制热性能的模型计算和结果验证，结果表明文章中使用两个平台完成的空调物理模型，可以很好的完成汽车空调最大性能的预测。

汽车空调；物理模型；一维模型

前言

汽车空调系统是汽车重要的附件系统之一，主要包括制冷系统、加热系统，实现车厢的制冷、加热、除霜、除雾功能[1]。汽车空调系统的好坏不仅影响上述功能，还会影响汽车经济性和舒适性。随着整车开发周期的缩短和计算CFD的发展，构建汽车空调模型，已经成为研究汽车空调性能一个重要的方向。

汽车空调包括制冷系统、空调箱、乘客舱，其物理模型需要考虑两相流、相变换热、空调箱和乘客舱复杂的结构，以及持续变化的外部环境和整车工作状态，这些因素导致汽车空调物理模型的复杂性。国内外学者使用不同的方法对汽车空调进行了建模研究。文献[2]使用Matlab构建微通道蒸发器和膨胀阀的集成建模和实验对比，文献[3-4]分别使用sinda/Fluint和Modelica完成制冷系统的建模，并基于模型对系统进行优化；文献[5]使用CFD建立的三维空调箱模型，进行空调箱内部气流、传热的分析和验证，文献[6-7]基于AMEsim建立制冷系统模型，并分别建立乘客舱单温区、多温区温度模型，完成制冷系统和乘客舱模型的联合运算，即完成汽车空调制冷过程的计算。目前文献较少涉及制冷系统、空调箱、乘客舱物理模型的联合运行，更少有文献同时完成最大制冷、制热性能预测的研究和应用。

本文介绍的汽车空调物理模型，制冷系统物理模型是基于AMEsim搭建，空调箱和乘客舱物理模型是基于Simulink搭建，两个平台搭建的物理模型均是基于热、流节点和能量平衡的一维模型，两个平台之间通过FMI实时交互数据，共同完成汽车空调最大制冷、制热性能预测，使用两个平台的好处是一方面发挥了AMEsim擅长两相流计算的优势，另一方面也避免了对已有成熟空调箱、乘客舱Simulink模型的重新建模的问题，也为模型在环提供便利。

1 制冷系统物理模型

1.1 压缩机物理模型

压缩机是汽车空调制冷系统的核心部件，虽然内部结构复杂，但在模型化过程中主要考虑对空调系统性能的影响最大的两大效率，即容积效率和绝热效率，其关联式[3]如下：

式中，0至s为绝热效率关联式系数，0至4为容积效率关联式系数，p为压缩机排气压力和吸气压力之比，R为压缩机转速(rad/s)。

1.2 热交换器物理模型

汽车空调制冷系统除压缩机外，主要包括两大换热器：蒸发器和冷凝器，虽然其结构比压缩机简单，但是其换热过程涉及沸腾换热、冷凝换热等相变过程，且制冷剂流动涉及两相流，所以换热器的模型是非常复杂的，为了完成模型的建立，适当的简化是非常有必要的，本文涉及两相流的模型均简化为均匀模型，即气相和液相的温度相同、流速相同。

制冷剂侧流体流阻的计算，首先需要建立流阻-热容节点，如图1为一个扁管内部一个R-C节点，其中C为热容节点，其控制方程为(3)，(4)；R为流阻节点，其控制方程为(5)，其沿程阻力损失计算使用Fridel关联式[8]。空气侧简化为多孔介质，不再赘述。

图1 制冷剂侧流阻-热容节点

为了完成换热器热流传递计算模型的建立，需要建立热容-热阻节点网络，如图2是其中一个管内制冷剂至管外空气的热量传递原理图，包括C-R-C-R-C节点，涉及管内壁面对流换热（式6）、管壁热传导、管外壁对流换热（式7）。

图2 热容-热阻节点网络

式中，h为内壁面对流换热系数（(2·K)），A为内壁面换热面积（2），T、T分别为制冷剂和壁面温度（℃），a、b、c分别为关联式系数。

制冷剂侧对流换热系数的计算，对于单相流区，采用Gnielinski关联式[9]计算，对于两相流区的沸腾换热使用VDI Heat Atlas (Vertical tubes)关联式[10]计算，对于两相区冷凝换热使用Shah关联式[11]计算。空气侧换热关联式系数可以通过蒸发器、冷凝器台架数据拟合获取。

1.3 膨胀阀物理模型

膨胀阀是制冷系统不可或缺的部件，其建模可以根据受力分析进行，也可以根据QC/T663-2000台架测试数据绘制的四象限图建模，为了保证模型的准确度，本文第二种方式。四象限图包括：感温包内冲注介质的温压特性，在给定感温包温度T下膨胀阀开度和蒸发器出口压力的关系，以及在给定高、低压力、过冷度时膨胀阀开度和流量的关系。

基于四象限，根据蒸发器出口温度T和时间常数计算感温包温度T（式8），根据第一象限可以计算膨胀阀开启压力P，根据当前蒸发器压力和给定感温包温度下膨胀阀开启压力计算给定感温包温度下的蒸发器出口压力P(T)，见式9，然后根据第二象限可以计算出膨胀阀的开度，根据第三象限可以计算出膨胀阀开度对应的参考流量dm，根据参考流量和当前的高、低压、制冷剂密度可以最终计算制冷剂的流量，见式10。

式中，P、P(T)分别为当前感温包温度下膨胀阀开启压力、给定感温包温度下膨胀阀开启压力(bar)P为当前蒸发器出口压力(bar)，P、P分别为当前冷凝器出口压力（bar）、蒸发器进口压力（bar），为当前制冷剂密度（kg/m^3），、、分别为第三象限参考工况下的冷凝器出口压力（bar）、蒸发器进口压力（bar）、制冷剂密度（kg/m^3）。

2 空调箱物理模型

空调箱内部包括空气滤芯、蒸发器、加热芯体、新风风门、温度混合风门、风量分配风门等主要部件，为了简化模型，本文空调箱风量分配来自台架数据，空调箱换热模型只涉蒸发器出口至风道出风口部分。

对于空调箱中的加热器芯体，其热源侧为发动机冷却液，另外一侧为空气，其换热过程都没有涉及相变，冷却液侧换热，使用Dittus-Boelter关联式：

对于空调箱壳体和管内空气的换热，以及风管和管内空气的换热，使用Sieder and Tate关联式[12]：

层流和紊流分别使用式12、13，计算Nu：

式中：Re、Pr分别为雷诺数和普朗特数，Len为流体流动方向长度(m)，d为水力直径(m)，、分别为流体在流体当前温度和壁面温度时的动力粘度kg/(m·s)。

3 乘客舱物理模型

3.1 热网络节点

乘客舱主体包括玻璃和车身，把玻璃和车身细分成单元节点，其中玻璃共六个单元节点，包括前、后挡风玻璃和四个侧窗玻璃，车身共十个单元节点，包括仪表板上、下部，后排座椅、后排衣帽架、车顶棚、地板和四个车门节点，每个单元节点有包括内、外两个表面温度节点（编号1-32）；乘客舱内的空气划分为四个温区（编号33-36）；此外，车外空气为节点37，太阳为节点38，天空节点为39，地面节点为40，节点之间有热量传递，各个节点均看成是具有集总参数的单元。车窗玻璃可以看作均匀介质，其导热系数可以通过试验测得，车身简化为多层导热问题。单元节点两侧均是对流换热，关联式详见文献[1]。

车身外表面时刻都在和周边的环境发生着辐射换热，对于车身、地面、天空的辐射换热可以采用斯蒂芬-波尔兹曼（Stefan-Boltzmann）定律。对于天空的发射率，采用Angstrom方程[13]获取。乘客舱内部是一个密闭的空间，其各个表面之间存在着相互的辐射换热，根据辐射换热的基本定律，可以得出第j个表面和第i个表面的辐射热量（W）。

3.2 计算模型建立

对于节点1到节点32，在任意时刻，流入任意节点的净热流率为：

式中q，q，q分别为j节点到i节点的传导热流率/2、对流热流率/2、辐射热流率/2；n为与节点i有换热关系的节点总数。

任意时刻，任意节点的温度：

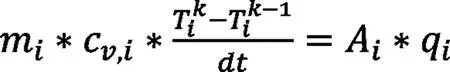
通过壳体各个区域进入乘客舱内的热量Q，同时考虑空调风量和温度对乘客舱内温度产生的影响，最终通过迭代计算出乘客舱内空气温度，其详细过程可以参考文献[14]。

4 实车验证

4.1 工况描述

为了完成上述物理模型验证，进行典型的热、冷环境风洞测试。典型热工况，环境温度38度，湿度40%，阳光强度1000W/m^2，空调模式为吹面，风量最大，温度设定最低，车速和其它空调参数见表1。

表1 热环境工况点

典型的冷工况，环境温度-20度，无阳光，空调出风方向为吹脚，风量5档，内外循环设定为外循环，温度设定为最高，工况1车速40km/h，持续20分钟，工况2车速100km/h, 持续20分钟。

4.2 试验结果

图3~7所示是在典型热环境、冷环境工况下空调最大制冷性能和最大制热性能试验数据和模型计算结果的对比。图3所示制冷系统中蒸发器空气侧出口温度试验数据和模型计算结果的对比。图4所示制冷系统中冷凝器制冷剂侧进口压力验数据和模型计算结果的对比；图5所示乘客舱模型前排左温区空气温度数据和模型计算结果的对比；图6所示为空调箱左侧脚步出风口温度试验数据和模型计算结果的对比；图7所示乘客舱模型前排左温区空气温度数据和模型计算结果的对比。

图3 蒸发器空气侧出口温度

图4 冷凝器制冷剂侧进口压力

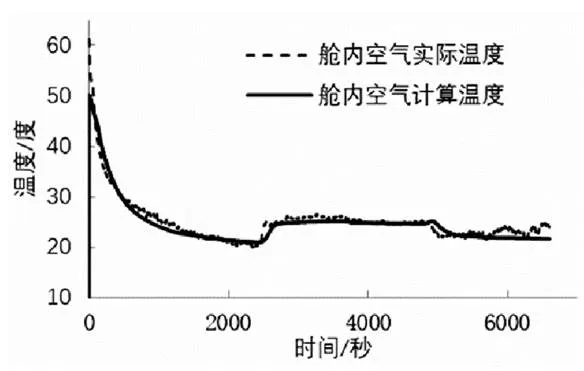
图5 乘客舱内空气温度

通过对比发现，无论对于极端的冷环境、热环境还是对于不同车速、阳光强度、空调设置，三个物理模型的最大制冷性能、最大制热性能计算结果都较好的和实际测量数据吻合，可以满足汽车空调工程计算的需要。汽车空调性能开发和空调控制器参数标定通常需要整车级别的风洞或道路测试，本文介绍的制冷系统物理模型、空调箱物理模型、乘客舱物理模型，涵盖汽车空调主要的物理模型，可以完成汽车空调最大制冷、最大制热性能开发前期计算。

图6 空调箱左侧出风口空气温度

图7 乘客舱内空气温度

5 结论

本文所述的制冷系统物理模型、空调箱物理模型、乘客舱物理模型，是针对汽车空调构建的一维物理模型，通过模型和实车的试验研究得出如下结论：

（1）基于热节点网络及能量平衡理论，使用AMEsim完成制冷系统一维模型的建立；使用Simulink对空调箱、乘客舱组成结构和环境因素等进行热流传递分析，完成空调箱、乘客舱一维物理模型建立。

（2）对制冷系统物理模型、空调箱物理模型、乘客舱物理模型，根据台架数据进行零部件级别的校准后，在典型的热环境和冷环境下，完成最大制冷和最大制热性能的计算，在风洞中完成整车最大制冷、最大制热测试，对比结果表明三个模型计算关键指标数据和测试结果非常接近，满足工程需要。

[1] 刘占峰,宋力.汽车空调[M].北京:北京大学出版社,2011:37.

[2] SasiKumar Muthusamy, Rangarajan Srinivasan. Development and Validation of Mini-Channel Evaporator Model Integrated with TXV for R134a Mobile Air-Conditioning System[R] SAE, 2016-28-0061, 2016.

[3] Terry J.Hendricks. Optimization of Vehicle Air Conditioning Syste -ms Using Transient Air Conditioning Performance Analysis[R] SAE, 2001-01-1734,2001.

[4] Marco Braun, Roland Caesar. Simulation of a Vehicle Refrigeration Cycle with Dymola/Modelica[R] SAE, 2005-01-1899,2005.

[5] Yang Chen, Philip Stephenson. Integrated Development and Valida -tion of HVAC Modules Using a Combined Simulation and Testing Approach[R] SAE, 2008-01-0832,2008.

[6] Shankar Natarajan, Sathish Kumar S, Ricardo Amaral, Sadek Rah -man. 1D Modeling of AC Refrigerant Loop and Vehicle Cabin to Simulate Soak an Cool Down[R] SAE,2013-01-1502,2013.

[7] Gautam Peri, Kuo-Huey Chen, Bahram Khalighi Saravanan Samban -dan, S. Sathish Kumar.Cool. Down Analysis of an HVAC System Using Multi-Zone Cabin Approach[R] SAE, 2017-01-0182,2017.

[8] Friedel, L.: Improved friction pressure drop correlations for horizon -tal and vertical two-phase pipe flow, European Two-Phase Group Meeting, Ispra, Italy, Paper E2, 1979.

[9] Gnielinski V. New equations for heat and mass transfer in turbulent pipe and channel flows[J]. Int Chem Eng, 1976,16:359-368.

[10] D.Verein(Ed), VDI Heat Atlas, VDI Verlag, 1993.

[11] Shah M M. A general correlation for heat transfer during film condensa -tion in tubes. Int Journal of Heat and Mass Transfer, 1979, 185-196.

[12] F.P. Incropera and D.P. DeWitt, "Fundamentals of Heat and Mass Transfer", fifth edition, 2002, John Wiley & Sons, Inc.

[13] Toby R. Marthews & Yadvinder Malhi & Hiroki Iwata, Calculating downward longwave radiation under clear and cloudy onditions over a tropical lowland forest site: an evaluation of model schemes for hourly data[R] Theor. Appl. Climatol . 2012, 107:461-477.

[14] 张磊,钱锐.自动空调乘客舱实时温度模型开发及应用[J].内燃机与配件,2019(2):201-204.

One-dimensional Physical Model Development & ApplicationforAutomobile air conditioning

Zhang Lei, Gong Xiaobin, Qian Rui

( Pan Asia Technical Automotive Center Co., LTD, Shanghai 201210 )

In order to predict the maximum refrigeration performance and heating performance of automobile air conditioning, based on the theory of heat, flow network node and energy balance, AMEsim is used to build the physical model of refrigeration system, Simulink is used to build the physical model of HVAC module and Cabin, and Co-simulation is used to complete the model calculation and result verification of the maximum cooling and heating performance of air conditioning. The results show that the physical model base based on two platforms can well predict the maximum perfor -mance of automobile air conditioning.

Automobile air conditioning; physical model; 1-D model

10.16638/j.cnki.1671-7988.2019.10.059

TK124

A

1671-7988(2019)10-172-04

TK124

A

1671-7988(2019)10-172-04

张磊（1984-），男，工程热物理专业硕士，中级工程师，就职于泛亚汽车技术中心有限公司，主要从事汽车空调系统开发、自动空调算法开发、标定工作。