基于改进的Lotka-Volterra种间竞争模型预测退化高寒草地人工恢复演替结果
吴晓慧,单熙凯,董世魁,*,高晓霞,许驭丹,张 曦,武胜男,胡 樱,温 璐,刘世梁,董全民,王文颖
1 北京师范大学环境学院, 北京 100875 2 北京师范大学天文系, 北京 100875 3 内蒙古大学生态与环境学院, 呼和浩特 010021 4 青海师范大学生命科学学院, 西宁 810008 5 青海大学畜牧兽医科学院, 西宁 810016
青藏高原的草地面积约占全国草地总面积的1/3[1],提供了牧业生产基地和生态屏障等生态服务功能。但是,由于受到气候条件的变化和人类活动的影响,该区50%—70%的天然草地已经退化[2]。为了有效遏制天然草地退化、提高草地生产能力,行之有效的办法之一,就是在失去牧用价值,难以自我恢复的极度退化草地上建植和培育高产、优质、稳定的人工草地[2],降低天然草地放牧压力,并通过人工草地植被逐渐恢复退化的天然草地。自20世纪80年代以来大面积的“黑土型”次生裸地的出现[3],人为干预下的高寒草甸恢复演替过程成为生态学家研究的热点问题,目前的研究主要集中在人工恢复与其他恢复措施间的差异性[4]、播种牧草的优化组合[5]及混播机理[6]、水肥调控[7]、群落生产力及稳定性变化[8]等,但对人工草地植物群落种间竞争关系及其生态效应的研究较为少见。在人工草地的演替过程中,竞争是塑造植被群落结构和动态特征的动力[9]。尤其是在青藏高原的人工草地植物群落中,由于各组分生态位高度重叠,种间竞争尤为激烈,植物群落稳定性难以维持,植物群落演替何时趋于稳定难以预测,各组分之间的竞争成为控制群落演替的主导因子[2]。因此,对人工草地各植物组分的竞争效应进行研究,将有助于我们厘清植被恢复过程、预测植物群落演替的方向,可以为退化高寒草地的人工恢复管理提供科学依据。
目前,利用生态数学方法构建的诸多数学模型在草地植被研究中的应用越来越广泛。其中,反应竞争-密度效应的数学表达模型以Logistic模型较为常见,但是该模型仅适用于实验室控制条件的竞争试验结果预测,对自然环境中的种间竞争关系预测较为困难。因此出现了许多改进模型,如Hallam模型[10]、Smith模型[11]等。从多物种竞争的角度出发,Lotka-Volterra种间竞争模型(简称LVM)是Logistic模型的一种延伸,其应用较为广泛。例如,王慧忠等[12]利用LVM求解牧草种群与放牧家畜种群的变化规律,林慧龙等[2]建立了适合高寒地区3组分禾草混播种间竞争机制的LVM模型。但是,由于青藏高原高寒地区植物群落演替的长期追踪监测较为困难,长时间序列的植物群落演替过程中的种间竞争关系鲜有报道。对于植物群落中种间关系的预测,也需要对传统的LVM模型进行修正,才能应用于自然条件下植物群落演替过程中的种间竞争关系预测。
本研究旨在通过野外调查和模型模拟,建立适合黑土滩型高寒人工草地植物竞争效应的LVM修正模型,从牧业生产和生态功能两个角度出发,将高寒草地植物群落的组分植物进行归类,结合不同恢复年限人工草地的实测组分植物的数量特征,通过计算机模拟研究改进后Lotka-Volterra系统的动力学行为,刻画不同恢复年限高寒草地植物群落各组分的时间演替特征,分析高寒草地不同组分植物的竞争结局,预测退化高寒草地人工恢复所需的时间限值,从而为退化高寒草地的人工恢复管理提供科学依据。
1 研究方法
1.1 研究区域概况
研究区域位于青海省果洛藏族自治州玛沁县大武镇,属于典型的高原山地类型。地理位置为34°21′—34°29′N,100°12′—100°29′E,平均海拔3800 m。气候类型为高原大陆性气候,春季干旱多风,冬季寒冷漫长,年均温约-3.9℃,年均降水量423—565 mm,降水多集中在6月—9月份,占年降水量60.0%。牧草生长季约156 d,无绝对霜期[13]。全年日照时间2313—2607 h,太阳辐射强,昼夜温差大。
土壤类型为高山草甸土,85%的草地为高寒草甸,植被多样性程度高,为发展畜牧业提供了重要资源。但受到人类活动诸如超载放牧、过度开垦等影响,加之气候变化带来的影响,大部分天然草地出现不同程度的退化,黑土滩问题突出[3]。黑土滩退化草地给区域生态、生产、社会经济等带来负面效应[14]。已有研究结果表明,黑土滩退化草地使用围栏封育自然恢复方法难以达到恢复标准,且最终会形成越来越稳定的毒杂草群落[15],而人工草地措施在一定程度上促进了黑土滩退化草地植物群落的恢复演替[16]。为了解决草地退化问题,该地区建植了大片人工草地,目前已有不同建植年限的人工草地。
1.2 数据来源
于2017年7—8月进行野外采样工作。在选取的研究区域内,选择13块不同建植年限的研究样地,均为冬春草场。这13块样地均为禾本科——垂穗披碱草(Elymusnutans)或草地早熟禾(Poapratensis)单播的人工草地,建植期分别为17a、15a、13a、12a、11a、10a、9a、8a、7a、5a、3a、2a、0a(春季新翻撒播地)。我们采用空间分布代替时间演替[17]的方法研究人工草地恢复演替过程中各组分的动态竞争。样地信息见表1。

表1 样地基本信息
在上述13个样地中,分别随机选取5个1 m×1 m的样方,统计各样方中每一个物种的物种数量(多度)。
1.3 数据处理
本文选取物种的种群数量来表征物种竞争力。将样地上的所有物种按不同的目的进行分组,基于统计的各样方中每一个物种的种群数量,利用Python计算出每一组分的种群数量之和。采用3σ准则对每个样地上的五个样方的数据进行综合,将数据取平均值作为该样地上各组分的种群数量之和。
2 模型的建立
LVM是研究种群对某些公共资源的竞争动态的简单模型,是经典的单种群增长的Logistic方程在种间竞争上的直接推广,因此又被称为种间竞争的Logistic方程[18]。已知LVM如下:
(1)
式中,N1、N2分别为两个物种的种群数量;K1、K2分别为两个物种的环境容纳量;r1、r2分别为两个物种的种群增长率;α为物种2对物种1的竞争系数,即每个N2个体所占用的空间相当于α个N1个体所占用空间;β为物种1对物种2的竞争系数,即每个N1个体所占用的空间相当于β个N2个体所占用空间。并且,N2种群中每个个体对N1种群的影响为α/K1,N1种群中每个个体对N2种群的影响为β/K2。
然而,LVM存在一定的局限性。模型中种群数量的改变与环境资源之间呈线性关系,不一定符合自然条件下的逻辑关系[19]。且实际情况中种群增长速度分布形式众多,一般不对称,与模型的预期存在较大的差别。只有当环境资源与种群所需要的资源供应数量相差很大时,才会出现方程中所描述的种群增长率随种群密度的增加呈线性递减的趋势[19]。为了使模型对于种群竞争规律具有更大的包容性,借鉴张大勇[20]、李新运[21]等对Logistic方程提出的改进,我们对LVM进行非线性化,提出以下改进:
(2)
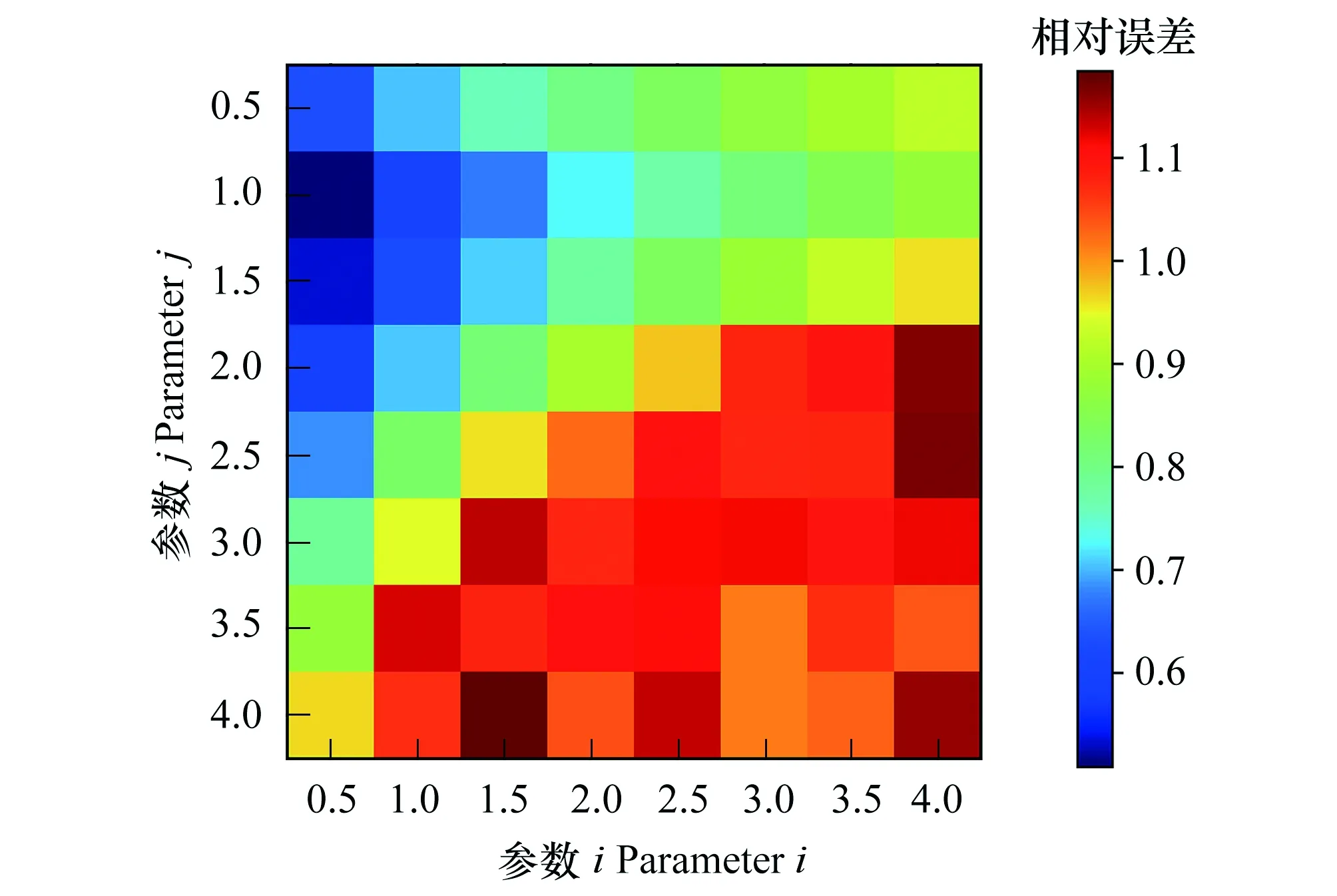
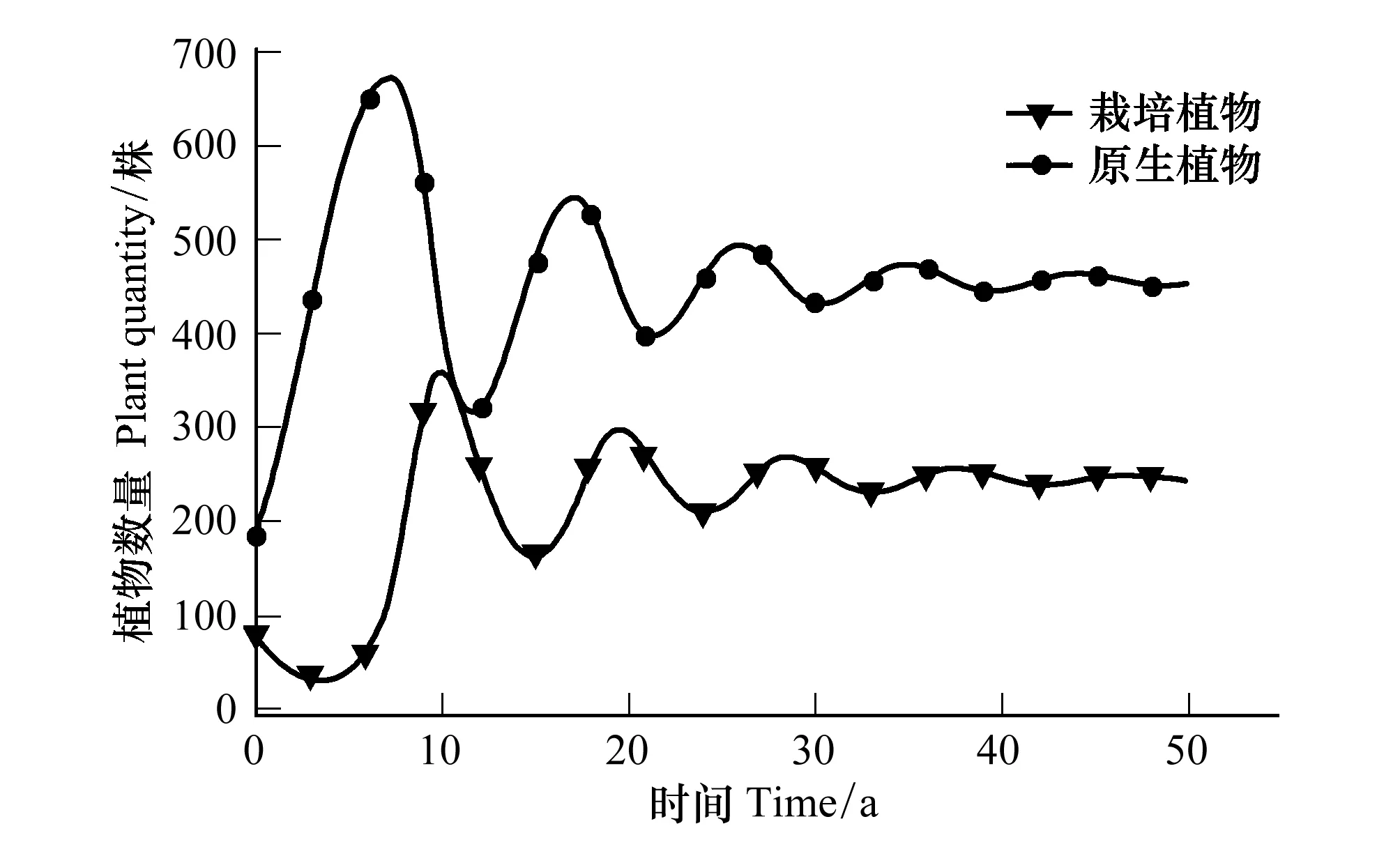
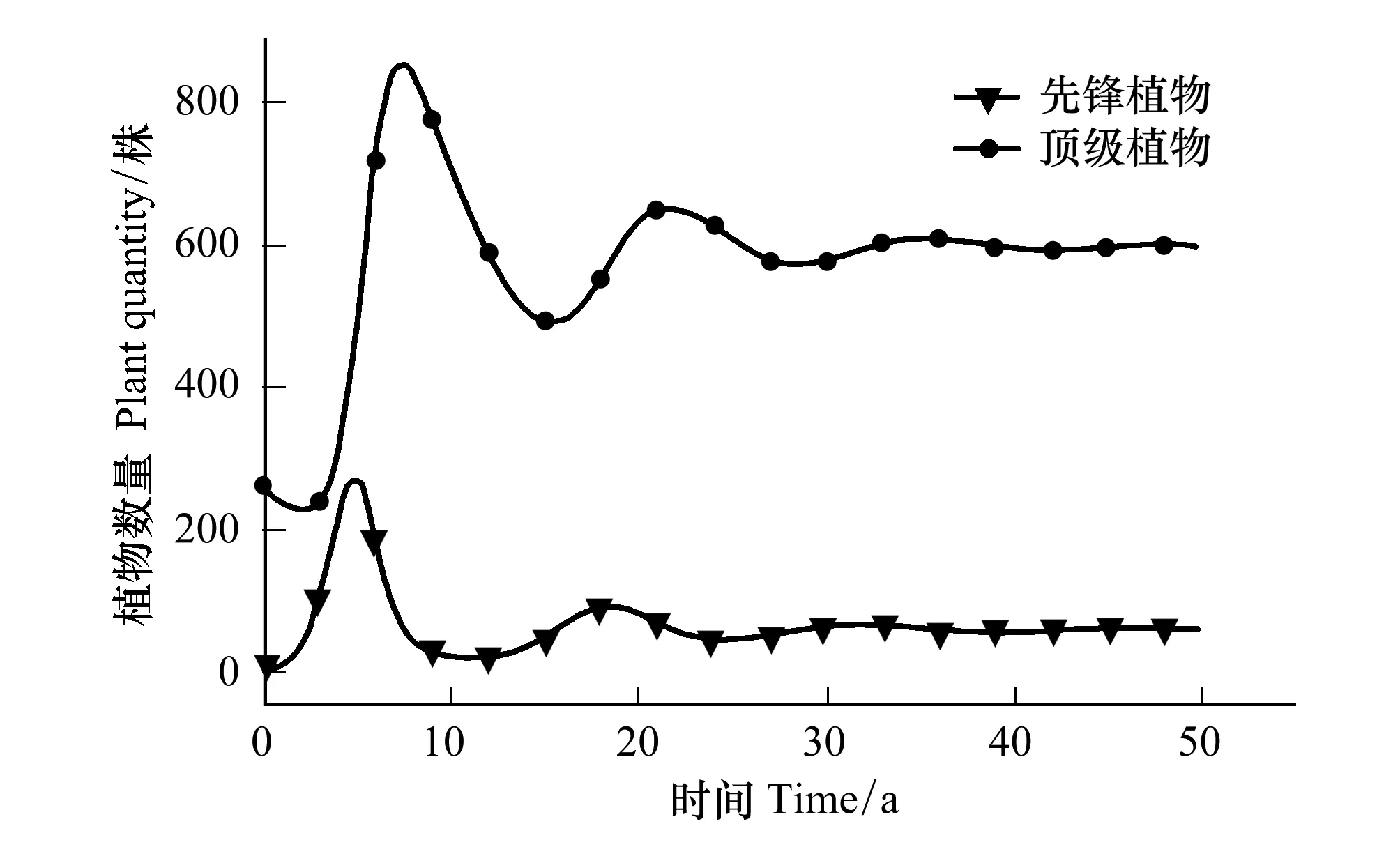
式中,i、j均为密度制约参数,取值范围为0 模型改进后,为求得微分方程组的数值解,首先需要证明该方程解的存在唯一性。为此,我们给出以下证明过程: 将方程(2)写成矩阵形式即: 利用Lipschitz条件,得到以下证明: 因为 令 所以 因为 an+1-bn+1=(a-b)(an+an-1b+…+abn-1+bn) 令 g(a,b)=(an+an-1b+…+abn-1+bn) 所以 所以 因为 所以 同理可证 所以上式满足Lipschitz条件,因此微分方程(2)存在唯一解,故改进后的模型在数学理论上可行。 在实际应用中,密度制约参数i、j的确定方法如下: 第二步:根据ODE算法求得微分方程(2)在不同i、j下的数值解; 第四步:循环Step 1—Step 3直至取遍所给定的所有i、j的组合; 第五步:画出不同i和j的组合对应的相对误差热图; 第六步:找出相对误差最小的情况下所对应的i、j组合,并画出此组合下的模型数值解N1(t),N2(t)趋势图。 为了全面反映人工恢复草地植物的竞争格局,将人工草地植物物种组分分为以下几组:(1)可食牧草与毒杂草;(2)栽培植物(垂穗披碱草、草地早熟禾)与原生植物;(3)先锋植物与顶极植物[22]。基于13块不同恢复年限人工草地的样地实测数据,用Python进行样条插值扩充数据量以保证拟合微分方程式系数时的稳定性,并得到建植17年内的实际恢复演替图。通过循环Step 1—Step 3得到确定的密度制约参数后,对以上改进的模型和LVM分别进行数值求解,得到改进的模型和LVM模拟的建植17年内的竞争演替图。分别与实际恢复演替图对比,得出改进模型对减小模型误差的贡献及其合理性。 需要注意的是,为了使相对误差热图中误差最小的部分(颜色最深处)得以突出体现,本文将该部分的误差数值进行了适当调整。因此,相对误差热图仅作对比参考以确定密度制约参数,具体的相对误差数值在文中各个具体验证部分展示。 对比图1可食牧草与毒杂草模型的相对误差热图中不同密度制约参数i和j下的误差大小可以看出,在该分组中,i=0.5,j=1.5时,模型模拟值的平均相对误差最小。利用Python求得计算机实验模拟模型: (3) 图1 可食牧草与毒杂草模型相对误差热图 Fig.1 Relative error thermography of edible forage and poisonous weed model 利用ODE算法求解微分方程(3),模拟建植17年内可食牧草与毒杂草的竞争情况并与实际恢复演替图进行对比(图2第一行)。同时对LVM进行求解,与实际恢复演替图进行对比(图2第二行),可以看出,改进后的模型模拟的结果比LVM模拟的结果更接近于实际恢复演替的情况。LVM模拟数值的平均相对误差为30.98%,改进后模型模拟值的平均相对误差为29.40%。其中,改进后模型对毒杂草的模拟值误差仅为25.31%,优于对可食牧草的模拟。模型改进后将平均相对误差降低了5.10%。由此可见,对LVM进行非线性化的改进,可以实现可食牧草与毒杂草的竞争及演替结局的有效预测。 图2 建植17年内可食牧草与毒杂草的模型预测与实际恢复演替对比图Fig.2 A comparison between model predictions and actual restoration successes of edible forage and poisonous weed within 17 years上下两行分别为改进后的模型和LVM的对比结果; 图中带有数据点的趋势线为实际恢复演替图,光滑的趋势线为模型模拟的结果;X轴为恢复时间(年),Y轴为种群数量(株) 对比图3栽培植物与原生植物模型的相对误差热图中不同密度制约参数i和j下的误差大小,在该分组中,i=2.0,j=2.5时,模型模拟值相对误差最小。利用Python求得计算机实验模拟模型: (4) 图3 栽培植物与原生植物模型相对误差热图 Fig.3 Relative error thermography of cultivated plants and native plants 同样的,利用ODE算法求解微分方程(4),模拟建植17年内栽培植物与原生植物的竞争情况并与实际恢复演替图进行对比(图4第一行)。同时对LVM进行求解,与实际恢复演替图进行对比(图4第二行),结果表明,改进后的模型模拟的结果比LVM模拟的结果更接近于实际恢复演替,尤其是在第8年后的效果十分明显。LVM模拟值的平均相对误差为65.27%,改进后模型模拟值的平均相对误差为55.24%。其中,改进后的模型对于原生植物的模拟误差为30.33%,效果优于栽培植物。模型改进后将相对误差降低了15.37%。由此可见,对LVM进行非线性化的改进以预测栽培植物与原生植物未来的竞争结局并分析演替规律优于LVM,对于较长时间尺度的预测是可行的,但仍需结合实际恢复演替图综合分析。 图4 建植17年内栽培植物与原生植物的模型预测与实际恢复演替对比图Fig.4 A comparison between model predictions and actual restoration successes of cultivated plants and native plants within 17 years上下两行分别为改进后的模型和LVM的对比结果; 图中带有数据点的趋势线为实际恢复演替图,光滑的趋势线为模型模拟的结果;X轴为恢复时间(年),Y轴为种群数量(株) 由图5先锋植物与顶极植物模型的相对误差热图得出,在该分组中,密度制约参数i=0.5,j=1.0时,模型模拟值相对误差最小。同样利用Python求得计算机实验模拟模型: (5) 图5 先锋植物与顶极植物模型相对误差热图 Fig.5 Relative error thermography of pioneer plants and climax plants 求解微分方程(5),模拟建植17年内先锋植物与顶极植物的竞争情况并与实际恢复演替图进行对比(图6第一行)。同时对LVM进行求解,与实际恢复演替图进行对比(图6第二行)。结果表明,改进后的模型模拟的结果比LVM模拟的结果更接近于实际恢复演替。LVM模拟值的平均相对误差为60.98%,改进后模型模拟值的平均相对误差为52.88%。其中,对于顶极植物的模拟误差为23.74%,效果优于先锋植物。模型改进后将相对误差降低了13.28%。由此可见,对LVM进行非线性化的改进以预测先锋植物与顶极植物未来的竞争结局并分析演替规律优于LVM,对于较长时间尺度的趋势预测是可行的。 图6 建植17年内先锋植物与顶极植物的模型预测与实际恢复演替对比图Fig.6 A comparison between model predictions and actual restoration successes of pioneer plants and climax plants within 17 years上下两行分别为改进后的模型和LVM的对比结果;图中带有数据点的趋势线为实际恢复演替图,光滑的趋势线为模型模拟的结果;X轴为恢复时间(年),Y轴为种群数量(株) 将模型模拟的预测年限延长至50年,得到自建植栽培植物后50年内可食牧草和毒杂草的竞争演替预测图7。图8为实际恢复演替图。结合图7、8可以看出,可食牧草在建植前7年内竞争力较强,呈直线上升,而7—10年急剧下降,在第10年达到最低,10年后呈现波动式上升;毒杂草在建植5年内种群数量不断上升,5年后下降,后期呈小幅度波动式上升,总体竞争力弱于可食牧草。从畜牧生产的角度出发,我们建议在建植7年后进行一定的人为干预,如施肥、灭鼠害以及适当去除杂草[23]等,以保证可食牧草持久的竞争力。从模型模拟预测图7来看,建植第20年可食牧草与毒杂草的竞争开始逐渐趋于平衡,可恢复放牧生产,进行适度放牧。此外,通过Mathematica求解模型平衡点有:(0,0),(540.15,163.58),(0,816.33)。其中,满足实际条件的稳态平衡点为(540.15,163.58)。通过该平衡点对应预测演替数据得知在人工草地建植后第28年,可食牧草与毒杂草的竞争达到平衡。 图7 可食牧草与毒杂草竞争演替预测图 Fig.7 Competition succession prediction of edible forage and poisonous weed 图8 可食牧草与毒杂草实际恢复演替图Fig.8 Actual restoration succession of edible forage and poisonous weed 人工恢复草地中的栽培植物与原生植物的竞争结果预测如图9所示。从实际恢复演替图10可以看出,起初栽培植物的竞争力较弱,呈现一定的下降趋势,但在第5年开始上升并与自然植物发生激烈的竞争,且二者之间的竞争比可食牧草与毒杂草之间的竞争更为激烈,尤其是在建植后5—8年之间栽培植物竞争力明显强于原生植物。人工草地建植8年后,栽培植物的竞争力下降,原生植物的竞争力上升;人工草地建植10年后二者协同生长。人工草地建植20年后,二者之间的竞争逐渐趋于动态平衡。因此,人工草地建植最初2—4a,要进行施肥、除杂草等人工辅助措施。 模型预测平衡点有(0,0)、(0,±710.70)、(-262.60±128.02i,-390.39±247.50i)、(-211.65±224.46i,-371.22±316.86i)、(297.55±47.91i,-352.43±272.22i)、(±688.43,0)、(245.83,456.46)、(-189.48±147.01i,477.03±23.03i)。其中满足实际条件的稳态平衡点为(245.83,456.46)。通过该平衡点对应预测演替数据得知,在人工草地建植第41年时,栽培植物和原生植物的竞争可以达到平衡。 图9 栽培植物与原生植物竞争演替预测图 Fig.9 Competition succession prediction of cultivated plants and native plants 图10 栽培植物与原生植物实际恢复演替图 Fig.10 Actual restoration succession of cultivated plants and native plants 先锋植物与顶极植物的竞争结果预测如图11所示。竞争预测图11和实际恢复演替图12可以看出,在种植人工草种后5年内,先锋植物和顶极植物协同增长,但在第5年后,顶极植物呈现出强烈的竞争优势,先锋植物竞争力直线下降甚至于第8年接近于0,先锋植物几乎被完全替代。因此,在高寒草甸种植栽培植物对先锋植物的生长抑制起到了一定的作用。然而第8年后,先锋植物呈现小幅度的波动式上升。相应的,顶极植物竞争力呈现下降趋势,第10年后继而呈现波动式上升。从模型预测演替图来看,自第20年起,二者之间的竞争逐渐趋于动态平衡,这一点与前文提及的可食牧草与毒杂草、栽培植物与原生植物的演替趋势基本保持一致。 图11 先锋植物与顶极植物竞争演替预测图 Fig.11 Competition succession prediction of pioneer plants and climax plants 图12 先锋植物与顶极植物实际恢复演替图 Fig.12 Actual restoration succession of pioneer plants and climax plants 模型预测平衡点有(0,0)、(597.95,59.44)、(0,2085.03)。其中,符合实际条件的稳态平衡点为(597.95,59.44),通过该平衡点对应预测演替数据得知在建植45年时,先锋植物与顶极植物的竞争达到平衡。在人工草地建植、辅助恢复的状态下,顶级植物的竞争力明显高于先锋植物。但预测结果显示,先锋植物在演替过程中保持一定微弱的竞争力,并未完全被顶极植物替代。 退化草地人工措施恢复的实践和研究起步相对较晚,人工措施下草地恢复过程中的牧草群落演替规律尚未被完全探明[4]。考虑到人工草地的恢复过程较长,因此,构建模型模拟各组分之间的竞争效应成为预测人工恢复结局的有效方法。目前,非线性动力学方法已经成为分析生态系统演变的主要工具[24]。基于前人对Logistic模型的改进,我们对LVM模型进行了非线性化,并利用Lipschitz条件证明得到其数学数值解的存在唯一性。 本文利用改进的LVM模型对青藏高原退化高寒草地人工恢复过程中对植物竞争和演替的结果预测,可以得出以下结论:(1)随着恢复年限的增加,栽培植物(垂穗披碱草和草地早熟禾)与原生植物在经历一个激烈的竞争阶段后逐渐趋于动态平衡后趋于稳定,说明人工种植垂穗披碱草、草地早熟禾等本土植物,可以促进青藏高原地区“黑土滩”型退化高寒草甸的有效恢复。这与冯瑞章[25]、杨慧茹[26]等的研究结果相一致,人工草地的群落组成、多样性、结构特征变化以及植物量动态指标变化基本上趋于稳定,土壤理化性质和种子性状的变化与群落演替相适应,是趋于稳定的动态变化,总体上趋于良性的方向发展[26];(2)在“黑土滩”型退化草地上, 通过多年生人工草地建设, 短期内可以恢复草地植被[27]。但是,王长庭等研究发现,杂类草(尤其是甘肃马先蒿)在建植4年的人工草地群落中开始局部入侵,在5—6年时入侵速度、入侵面积达到高峰期[24]。周华坤等的研究也表明人工草地在建成后4年内植物群落由“生产稳定性”急剧向“生态稳定性”转化,呈现出明显的退化态势[28]。本文研究则发现可食牧草、栽培植物和顶极植物均从第7年开始竞争力出现明显下降的趋势。并且,王启兰等表明人工草地建植后第7年,原群落优势种的丰富度明显下降, 主要以杂类草为主, 群落处于退化阶段[29]。因此,人工草地的恢复管理中,建议建植后第4年及7—10年间进行适度的人为干预,如施肥、灭鼠害以及适当去除有毒有害杂草等[30];(3)高寒地区“黑土滩”型退化草地的恢复需要较长的时间,王启兰等人在研究中发现,至少在建植后第14年,群落呈相对稳定的状态[29]。本文各植物组分的竞争预测结果则表明,“黑土滩”型退化草地进行人工恢复至少需要20年以上,才会获得较为稳定的植物群落。同时,有大量研究表明,放牧干扰对混播人工草地的稳定性[31]、土壤理化性质[32]、草地群落特征[33]和牧草营养[34]等方面具有显著影响。因此,从畜牧生产和草地恢复的角度出发,应在恢复20年时进行适度放牧。 通过对青藏高原退化高寒草地人工恢复过程中植物竞争及演替预测来看,改进后的LVM模型存在以下优点:(1)将模型非线性化使之成为了具有自适应性的非线性制约种群竞争模型,对于种群的增长、竞争模式具有更强的包容性;(2)从误差热图可以看出,改进后的竞争模型相对误差降低了10%以上,更接近于实际恢复演替的情况;(3)对模型的动力学行为的研究有助于预测人工草地各组分间的竞争结果,从而判断其恢复演替状况。但是,改进的模型也具有一定的缺点:(1)与实际演替图相比,模型对短期竞争效应的模拟能力较弱,因此在实际应用中,需将模型预测与实际监测结果相结合综合分析;(2)对于密度制约参数i和j的确定,由于受到计算机运行速度和算法优化等因素的制约,对i和j的取值间隔不够密集,应采用更多、更密集的i和j进行循环模拟以寻求更小的相对误差。在未来的研究中需要进一步发展和完善LVM模型,使其更加准确、合理地预测高寒草地人工恢复演替的结果。2.1 模型解的存在唯一性
2.2 模型的求解

3 模型的验证
3.1 可食牧草与毒杂草的竞争关系

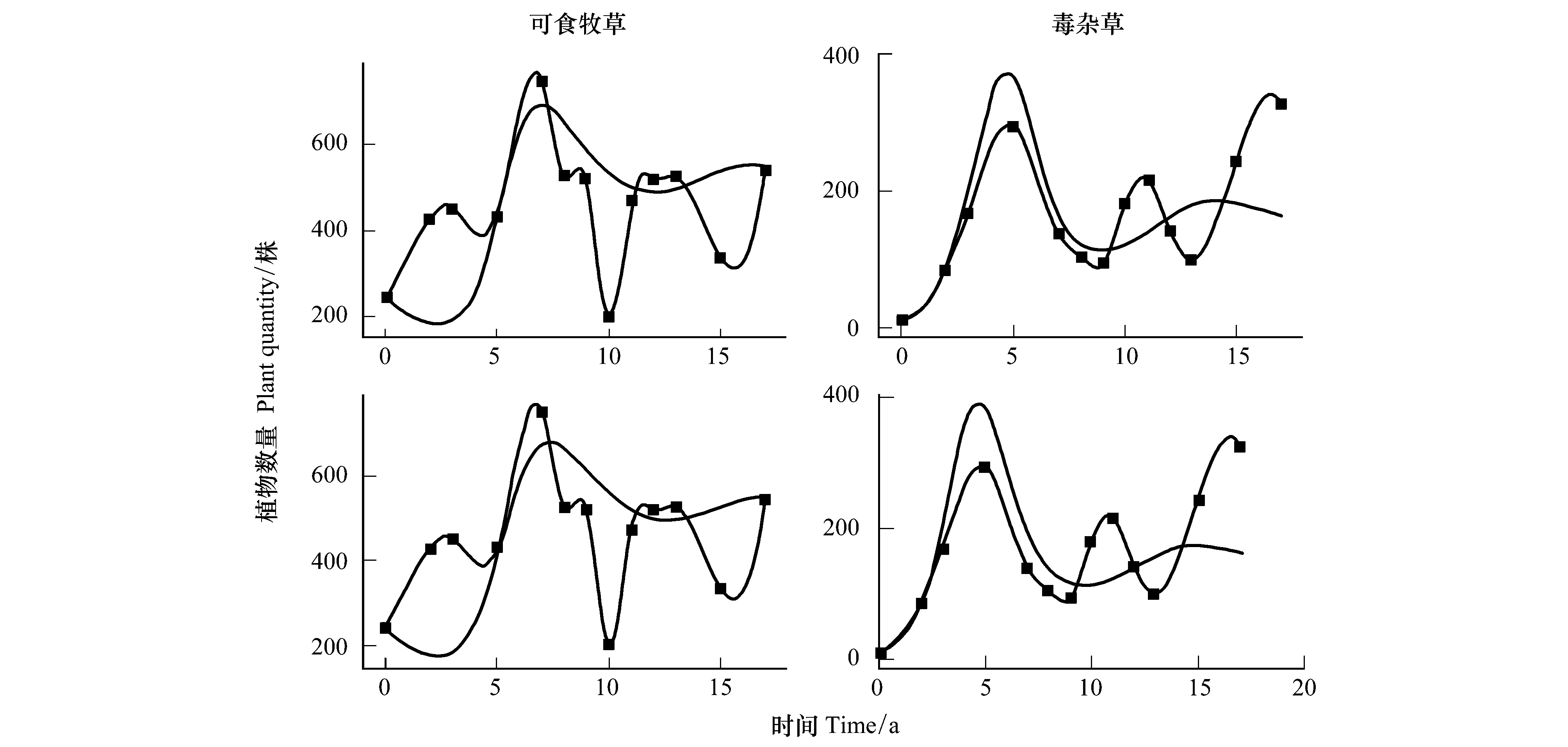
3.2 栽培植物与原生植物的竞争关系

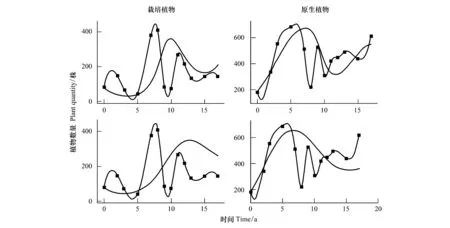
3.3 先锋植物与顶极植物竞争关系

4 竞争结果预测
4.1 可食牧草与毒杂草竞争结果

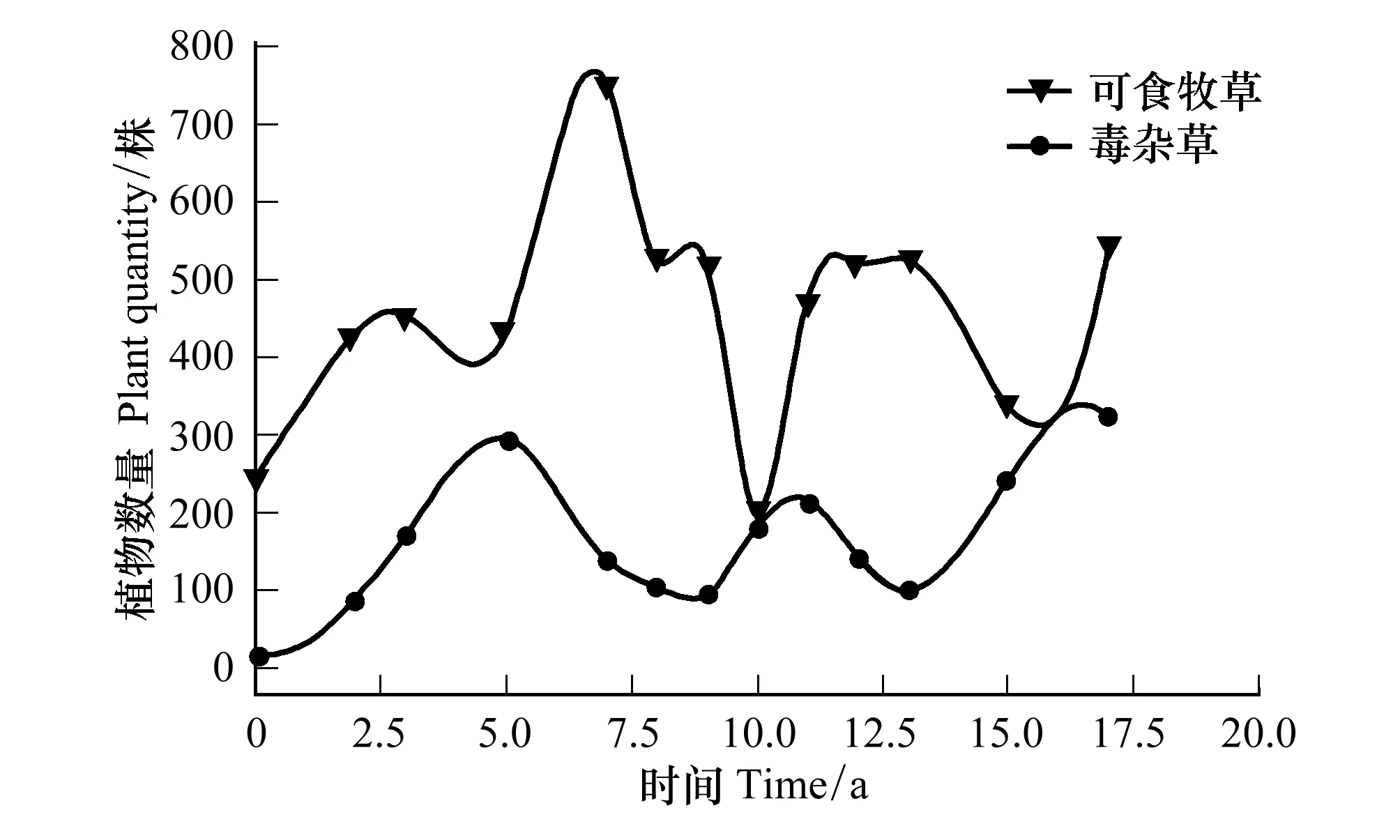
4.2 栽培植物与原生植物竞争结果

4.3 先锋植物与顶极植物的竞争结果

5 结论与讨论

