“退”“推”之间“玩”出智慧*
——六年级《玩数学棋》一课的教学与思考
【设计理念】
1.“玩”中碰壁,问题让智慧生根。
在现实教学中,数学教师虽然都致力于儿童思维能力的培养,可有时收效甚微。究其原因,儿童常常因为面对的问题是“伪问题”而兴致不高,内驱力大打折扣,致使其缺乏主动思考的意识与能力。那么,怎样寻找“真问题”?怎样让儿童的内心长出“真问题”呢?只有让儿童有真实的在场感,他们才能真正把面临的问题视作自己的问题,才能有积极的心向,主动寻找解决问题的策略。康德说:“教育即自由。”自由既是儿童的天性,也是需要我们为他们创造的条件。“爱玩”是儿童的天性。那么,怎样让儿童以“玩”的精神参与数学学习,让儿童自由地“玩”,创造性地“玩”,玩出智慧呢?在教学中,为儿童创造值得“玩”的场域很重要,因为儿童在能玩而又不能驾驭的矛盾中,各种问题就自然产生了,智慧就有了“抓地力”。
2.“玩”中探索,困难驱智慧生长。
问题越明晰,解决时的方向就越明确。面对各种问题,怎样通过比对、抽象让儿童直面本质问题,并梳理出主线问题呢?于是,“接下来怎么思考呢?”就成了直接驱动儿童思考的主线索。教学中,教师往往更在意怎么帮学生解决眼下的问题,而深陷于寻找具体的步骤、方法或策略。事实上,“你是怎么想到的?”才是最重要、最值得思考的问题。所以,教学中更需要让学生始终抱有客观审慎的态度,学会反向思考——“我之所以不能前进,困难在哪里?”,退到自己能确定、能解决的问题处,然后不断扩大思考范围,挖掘思考深度,从而解决问题。
3.“玩”后自省,方法助智慧生成。
获得问题解决的喜悦是教学追求的目标之一,但不是终极目标,沉淀下经验、方法才可能生成智慧。所以,在教学中,要让学生有静下来再思考和慢下来再玩味的机会。如此,才能促进他们完善认知结构,提升应对未来的能力。
【教学目标】
1.通过玩数学棋积累数学活动经验,体验研究问题的策略,并在此过程中着力培养推理能力。
2.在交流分享中学会辩证地倾听,并有理有据地表达自己的推理过程。
3.在活动中进一步感受数学的亲切感与趣味性。
【课堂实录】
一、谈话:引出玩棋游戏
师:同学们,今天我们一起来玩(板书:玩)。说一说,你会玩些什么?
生:会玩游戏、围棋、扑克、篮球、围棋……
师:同学们会玩的东西真多!如果你就只是玩玩,很容易就没兴趣了;如果边玩边思考,你就会玩出水平,甚至还能玩出智慧。今天,我们就一起来玩数学棋(板书:数学棋),看看能否玩出新的体会。
二、比赛:思考玩棋中的问题
1.比赛,好奇中引发问题。
(图1)
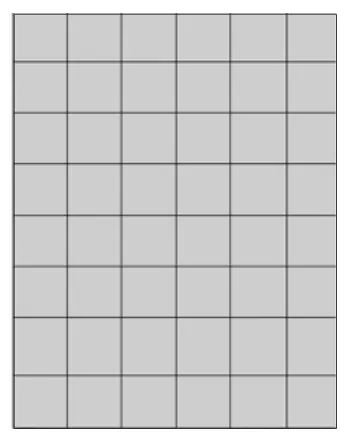
(1)教师讲解游戏规则:瞧!这就是棋盘(如图1),左下角有一个红旗(放上红旗磁块),表示终点。在棋盘右上角有一枚棋子(放好黑色磁块),两人轮流移动这枚棋子,每人每次只能向左、下或左下移动一格(板书:),谁先移入红旗格谁就获胜。
(2)指名一男一女两个学生玩
师:你俩谁先走?
男生:女生优先。
师:真有风度!其余同学注意观察,看他们是否符合规则。好,开始!
很快,比赛结束,男生输了。
师:我宣布,这一轮,女生获胜。(举起女生的手,然后采访男生)刚才你输了,想不想再玩一次?(男生欢喜地点头)
师:大家猜猜他这时在思考什么问题?
生1:先走,还是后走?
生2:朝哪个方向走呢?
师:同学们说的其实是同一个问题——怎样才能赢呢?那么,有没有必胜的策略呢?
2.尝试,初步探明研究方向。
(1)同桌尝试玩2次,思考初步的方案
师:同桌的桌上有这样的材料袋,先将笑脸磁块放到终点格,再找到起点格。同桌共玩2次。边玩边思考:怎样才能必胜呢?
同桌玩,教师巡视,收集学生的想法。
(2)谈话,让学生明确研究方向
师:刚才,同学们玩得很高兴,你们找到必胜的对策了吗?(少数人举手)
生1:我觉得后走的肯定赢,我两次都后走的,两次都赢了。
生2:反对,我也后走的,没有赢。
生3:我先走的时候也赢过。
师:呀,看来这个问题挺复杂。想一想,它究竟复杂在哪里?
生1:方向很多,情况很多,很复杂。
生2:而且你不能控制对方,指定他怎么走,所以有很多不确定因素,太复杂了。
生3:棋盘这么大,步数又多,很复杂。
师:面对这么复杂的问题,应该从哪里开始研究呢?(学生思考,但无所得)
师:你们真是下到最后一步才知道输赢的吗?
生1:我们到“田字格”里就知道了。
生2:我们到“九宫格”就知道了。
师:那我们就从最简单的、能确定的那一步开始研究,好吗?
师(出示2×2情况):刚刚有人说到这种情况就可以确定了,谁能解释解释?
生:谁先到这三个虚线圈格中的任意一格(如图2),对方都可以直接进入红旗格,所以这三格是必输格。

(图2)
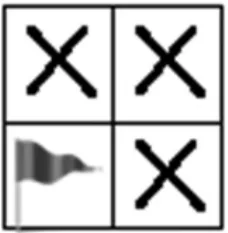
师:我们给这三个必输格做个记号“×”(如图 3)。哎,我们要找必胜的方法,却找到了必输点,这对我们找必胜的方法有用吗?
(图3)
生:有用。可以借助它往外推。
师:那么,接下来,我们该怎么研究?
生:我们可以把棋盘扩大,研究3×3情况。
同桌研究,相互交流;教师巡视,然后请一对同桌发言。
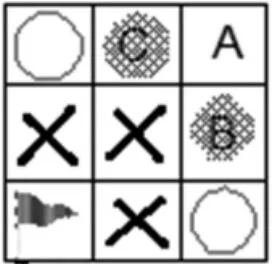
生1:谁先到图中2个圆圈格(如图4),谁必胜。因为到了圆圈格对方只能向下(向左)走,这样对方只能进必输格,对方必输,我必赢。
(图4)
生 2(补充):B、C 有两种可能,不能保证自己必胜。但A不管怎么走都可以抢到必胜格。所以A点也是必胜格。总之,谁先抢到这三个格,谁必胜。
师:我有个疑问,我先到A,万一对方向左下方走呢?这种情况你们没说哦。
生:哈哈,那对方就自投罗网了。进了必输格,必输了呀。

(图5)
师:好的,我们用记号“√”表示必胜格(如图5)。谁先到必胜格,谁就有了必胜的方法。看来,只要我抢到必胜格,我肯定就赢了。
师:这么大的棋盘,我们目前只研究出这一小块,接下来怎样研究?有没有更好的方法找到必胜的策略呢?
3.深究,推理标记中明确对策。
(1)自主研究:先同桌研究,接着4人小组讨论,推选代表准备发言。
(2)汇报,交流
第一组汇报(边说边借助教师的棋盘演示):我们接着研究了4×4情况,发现谁先到4×4外围中任意一格,对方都能抢先到3×3外围中的必胜格,所以4×4这一圈都是必输格。那么5×5一圈中必有必胜格,因为每人只能走一步,所以必胜格是间隔开的,再根据方向就能确定必胜格了。以此类推,就能找到所有的必胜格了。
第二组汇报(边说边借助教师的棋盘演示):我们发现1个必胜格周围总有3个必输格,再根据如果只从一个方向考虑必输格后就是必胜格,能推得整个棋盘上所有的必胜格。
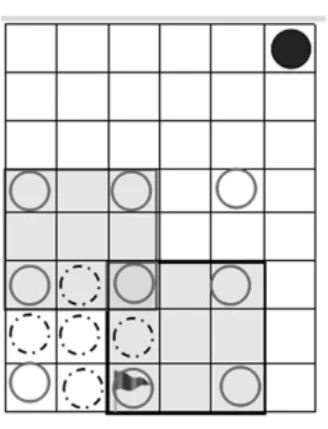
第三组汇报:我们是用九宫格来思考的,红旗格其实就是一个必胜格,我们假定这个必胜格在这里,就相当于把整个九宫格一起复制,移动到这里(如图6),这样就能用之前的方法确定这个九宫格里的必胜格,再用这样的方法就能找到所有的必胜格。
(图6)
师:谁听懂了他们的研究成果,他们的研究方法与第一、二组有什么不同?
生:第一、二组都是借助必输格来推想必胜格的,第三组是借助必胜格直接推的,也就是在3×3情况的基础上直接用模块覆盖的方式推理出来的。
师:变换研究基点,可以直接推理得到结果,真的非常巧妙!数学研究就是这样,要善于借用已经研究出的成果来研究新的问题。
(3)观察,发现
师:现在谁愿意和我玩数学棋?
生:我来下,但必须得让我先走。
师:好的,看你小,就让你先走。
师:为什么还没下完棋,你们就判定他赢了?谁来解释?
生:先走的人每一步都能抢到必胜格,所以他必胜。
师:请同桌再玩,体会体会赢的对策。
三、回顾:提炼玩棋中的收获
师:此刻,让我们静下心来,回顾刚才寻找必胜对策的整个过程,你有什么特别想和别人分享的?谁能简单地说一说?
生1:面对复杂的问题,一时不知道从哪里入手,可以从简单的、能确定的地方开始研究。
生2:也可以在初步研究的基础上,把这一步研究的成果打包、复制、粘贴来进行研究,这样更快捷。
师:是的,面对复杂的问题,最好的对策就是“退”,退到最简单又能保持原问题本质的地方开始研究,再以“退”为“进”,不断推测、推想、推理,把简单问题的研究成果“推”广到更复杂的情况,从而解决问题。
【教后反思】
从教22年,笔者由最初关注教学技艺的增长慢慢转变为关注儿童的成长,关注教儿童带得走的数学,努力构建逻辑与直觉、理性与感性、文化传递与创造兼备的课堂生态,以期促进儿童成为敏于反思质疑、自省自纠、善于“悟”的人。上述教学中,笔者努力构建一个充满自省意味的课堂,让儿童在“退”“推”之间玩出智慧。
1.一“省”主要问题。
课始,男女生代表在擂台赛中比拼,“纯玩”中似乎全凭运气,学霸在这里也不管用了。输了的学生自然想再玩一次,教师并没有立刻让他们玩,而是利用一句“猜猜他在思考什么”引发学生思考。在“先走”还是“后走”的辩论中,在不同方案的预设中,引导学生第一次反省:有没有必胜的策略呢?并带领学生抓住这个主线问题开启了探究之旅。
2.二“省”研究路径。
真正的探究充满未知——方向未知、路线未知、成功与否未知。怎样让儿童有兴趣并有信心探索,即使束手无策也要努力思考,坚信也许答案就在下一个转角呢?(1)“想一想,它究竟复杂在哪里?”学生有时会囿于困难中受伤的情绪,而并未理性思考究竟难在哪里。教师此时的点拨就显得尤为重要。在明确困难的过程中,学生悟的方向太多,就可以分类思考;棋盘太大,就可以缩小思考范围;步数太多,不能控制对方怎样走棋,就从能确定的地方入手。这样的自省活动有助于学生理清思考的方向与路径。(2)“你们真是下到最后一步才知道输赢的吗?”解决问题难,并不是难在怎样解决这个问题,而是难在“你是怎么想到的”。教师一语惊醒梦中人,让学生明白:复杂的问题可以从简单的、能确定的部分做起。
3.三“省”优化策略。
在思考问题的过程中,学生有时会陷入细小环节而忽略主线问题。当学生为研究清楚了2×2情况而欢呼时,教师引导他们内省:我们要找必胜的方法,却找到了必输点,这对我们找必胜的方法有用吗?事实上,在曲折的研究过程中,学生需要时时问自己“这对我的研究有价值吗?”“接下去怎样研究?”“怎样逼近我要寻找的答案?”在学生研究完2×2、3×3情况后,教师没有让学生按惯性走下去,而是以“这么大的棋盘,我们目前只研究出这一小块,接下来怎样研究呢?有没有更好的方法找到必胜的策略呢?”这个问题来引导学生不断突破思考阈限。学生或借助必输格来推必胜格,或借助必胜格环绕3个必输格来平铺推理,或通过简化方向一类一类地思考来推理,或直接将九宫格复制粘贴研究。在“复制粘贴法”出现时,学生连连发出赞叹声、鼓掌声,甚至有学生由衷地说:善于利用已有的成果真重要!
4.四“省”经验方法。
就在学生终于探得解决问题的策略,沉浸在成功的喜悦中,感受到原来秘诀如此简单时,教师引导学生从高涨的、热闹的气息中抽离出来,静思探索过程,用简单的语言分享收获。让学生悟得:面对复杂的问题,可以退到最简单而又不失其本质的地方,从能确定的简单之处入手寻找方法,再以探得的成果为基础,不断推想、推测、推理,从而化复杂为简单,最终成功地解决问题。
总之,在“玩”的过程中,学生一次次跌倒思考,又一次次起身前行,在“退”“推”之间,玩出了智慧。

