秸秆还田下土壤水分时间稳定性与玉米穗质量的相关性

刘继龙 任高奇 付 强 张玲玲 李佳文 于 凯

(1.东北农业大学水利与土木工程学院， 哈尔滨 150030； 2.东北农业大学理学院， 哈尔滨 150030)

0 引言

东北黑土区是我国重要商品粮基地，受该区特殊自然因素及人为因素影响，黑土区土壤退化严重，土壤保水和供水等性质不断恶化。因此，科学合理地利用黑土区农田土壤水分显得尤为重要。秸秆还田是改良土壤结构、提高土壤保水和供水能力以及增加作物产量的一个重要手段[1]，在解决黑土区土壤退化，合理调控、管理和高效利用农田水分方面得到广泛应用，目前国内外学者围绕秸秆还田对土壤水分和作物产量的影响已进行了诸多研究[2-3]。进行农田水分调控和管理，需要掌握农田土壤水分最低含量、最高含量和平均状况等信息。土壤水分时间稳定性[4]是土壤水分的一个重要特征，研究时间稳定性可以确定土壤水分代表性测点，通过代表性测点可以掌握研究区土壤水分最低含量、最高含量和平均状况等信息[5]，同时可以减少土壤水分测点数和观测次数，省时省力。目前国内外学者从不同土地利用类型[6-8]、不同土层深度[9-10]、不同气候区[11-12]和不同空间尺度[13-14]等方面研究土壤水分时间稳定性，并取得了很多成果，但没有关于秸秆还田条件下农田土壤水分时间稳定性的研究。农田土壤水分估算、调控和管理目的是为了创造有利于作物生长的水土环境，关于土壤水分时间稳定性与作物关系的研究也非常缺乏。因此，本文利用联合多重分形等方法，研究秸秆还田条件下黑土区农田土壤水分时间稳定性及其与玉米穗质量在单一尺度和多尺度上的相关性，以期为秸秆还田条件下黑土区农田土壤水分估算与管理以及作物产量提高提供理论基础与依据。

1 材料与方法

1.1 采样点布置

试验地(96 m×96 m)位于东北农业大学向阳试验示范基地，将试验地分成64个12 m×12 m的正方形网格，采样点设在每个12 m×12 m的网格中心(图1)，土壤水分采样点由南向北分为8行，采样点序号从第1行由西向东排序，第1行排序结束后，继续从第2行由西向东排序，以此类推，直至所有采样点排序结束。在每个采样点都埋设1 m长的TDR土壤水分探管，分别于2017年6月6日、6月19日、6月26日、7月2日、7月12日、7月28日、8月2日、8月5日、8月11日、8月19日、8月24日、8月29日、9月12日，利用TDR土壤水分测量仪测定每个采样点0～20 cm、20～40 cm、40～60 cm、60～80 cm土层的土壤含水率。试验地2016年种植玉米，玉米成熟后，利用收获机收割玉米，同时将粉碎的秸秆留在地表。2017年4月24日翻地起垄，翻地深度为20～30 cm，翻地时将2016年留在地表的玉米秸秆埋入土壤。2017年4月26日利用播种机进行玉米播种，品种为“九单48”，播种时，同时施用倍丰复混肥料，参考当地施肥标准，使用量为300 kg/hm2，玉米生长期间追施昆仑尿素(2017年7月8日)，使用量为360 kg/hm2，试验地没有灌溉，采用天平测得玉米穗粒质量和穗轴质量。

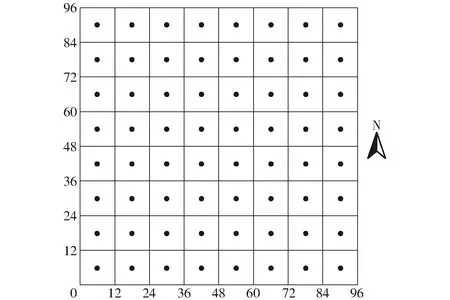
图1 取样点空间分布图Fig.1 Spatial distribution of sampling site

1.2 研究方法

(1)相对偏差

测点i处测定时间j时土壤含水率θij相对偏差δij的计算公式为[4]

(1)

其中

式中n——观测点总个数

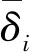
(2)

式中m——试验测定总次数

任一测点i处土壤含水率相对偏差的标准差σ(δi)的计算公式为

(3)

当某样点平均相对偏差为0时，该样点代表研究区土壤含水率平均状况；当某样点平均相对偏差为正值或负值时，该样点土壤含水率分别高于或低于研究区土壤含水率平均状况。某样点相对偏差的标准差越小，该样点土壤水分的时间稳定性越强；在选取代表研究区土壤平均含水率的样点时，遵循样点平均相对偏差接近于0(在±5%之内视为接近于0)，且其标准差较小的原则[7]。

(2)联合多重分形

利用联合多重分形方法确定2个变量在多尺度上的相关性时，需要确定的联合多重分形参数为α(q1,q2)、β(q1,q2)和f(α,β)，计算公式为[15]

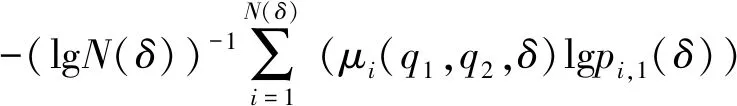
(4)

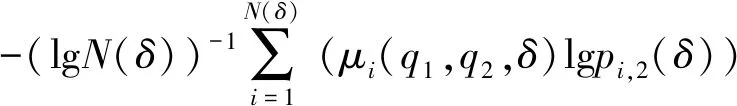
(5)

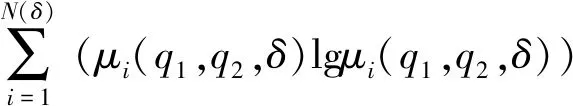
(6)

其中

式中δ——尺度

N(δ)——尺度为δ时划分的网格数

pi，1(δ)——变量1的质量概率

μi，1——第i处变量1的值

pi，2(δ)——变量2的质量概率

μi，2——第i处变量2的值

q1、q2——实数

α(q1,q2)——变量1的联合奇异指数

β(q1,q2)——变量2的联合奇异指数

f(α,β)——变量1和变量2联合奇异指数的维数分布函数

2 结果与分析

2.1 秸秆还田条件下土壤含水率与玉米穗质量的经典统计特征

由表1可知，取样时间范围内不同土层土壤平均含水率分别介于12.15%～18.77%、12.79%～18.93%、12.24%～17.03%、14.61%～20.08%；变异系数分别介于0.167 8～0.284 8、0.130 2～0.192 3、0.105 4～0.226 7、0.074 7～0.176 9，0～20 cm、20～40 cm、40～60 cm土层土壤含水率为中等变异，6月6日至8月2日60～80 cm土层土壤含水率为弱变异，8月5日至9月12日60～80 cm土层为中等变异。玉米穗粒质量、穗轴质量的平均值分别为214.28、30.18 g，变异系数分别为0.232 0、0.268 7，均为中等变异。

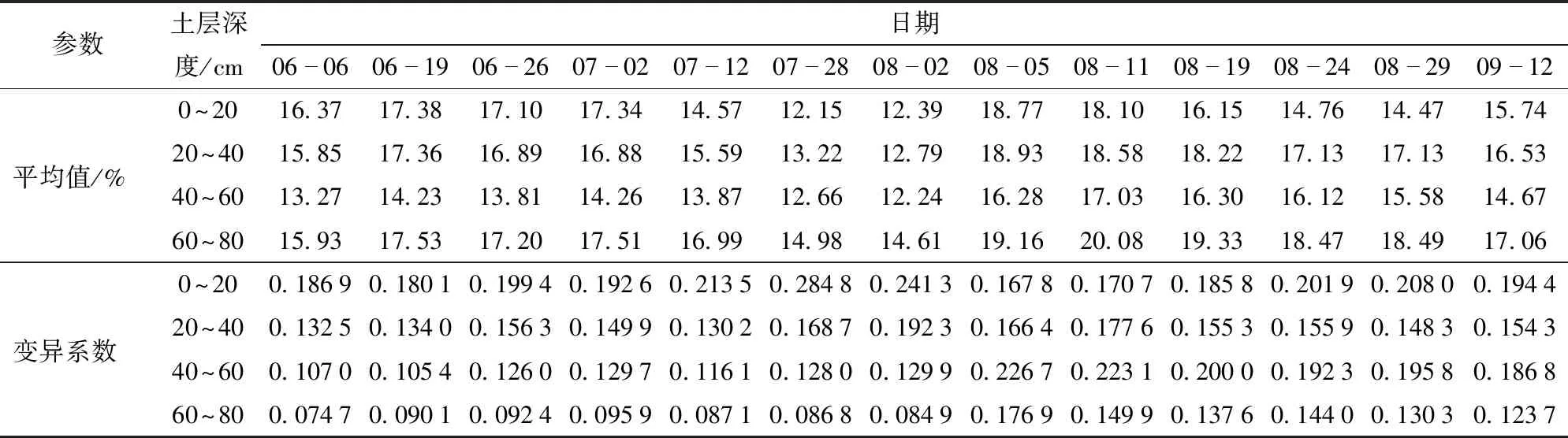
表1 土壤含水率经典统计特征值Tab.1 Statistical characteristics values of soil water content

2.2 秸秆还田条件下土壤含水率的相对偏差分析

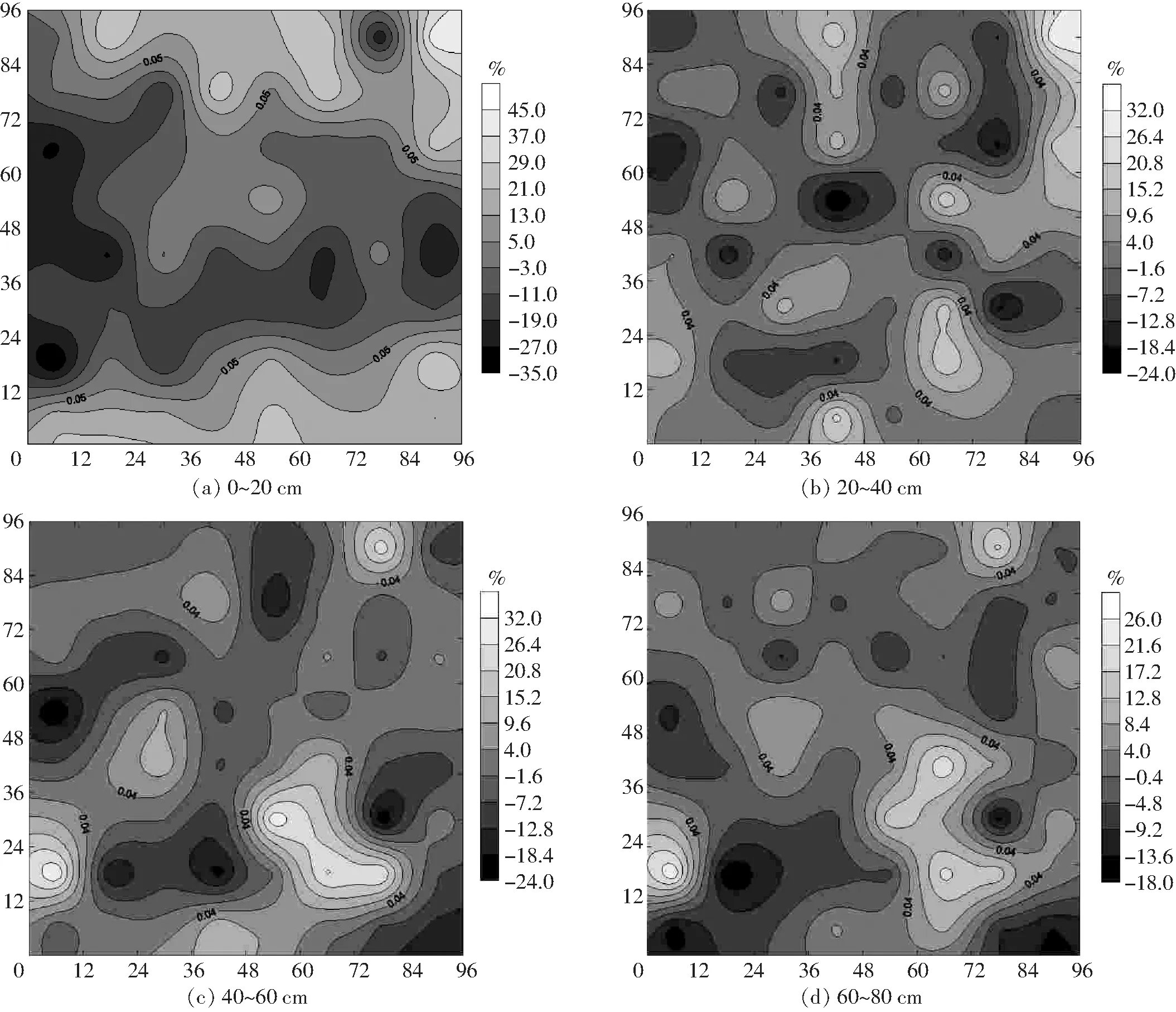
图2 土壤含水率平均相对偏差等值线图Fig.2 Contour maps of mean relative difference of soil water content

由图2可以看出，较深土层(40～60 cm和60～80 cm)土壤含水率平均相对偏差空间分布特征的相似程度较高。不同土层土壤含水率平均相对偏差的波动幅度分别为79.59%、55.74%、55.65%、43.86%，波动幅度随土层深度增加而减小。不同土层土壤含水率平均相对偏差的最大值均大于最小值的绝对值，与高磊[16]和HU等[17]的研究结果一致，ZHAO等[18]认为土壤质地与土壤结构对土壤含水率有重要影响，是导致平均相对偏差最大值大于最小值绝对值的一个原因，因此，需进一步考虑黑土区土壤结构及性质对土壤含水率平均相对偏差的影响。

从图3可看出，较深土层(40～60 cm、60～80 cm)土壤含水率平均相对偏差标准差的空间分布特征具有较高的相似程度。不同土层土壤含水率平均相对偏差标准差的波动幅度依次为87.50%、42.19%、34.70%、20.76%，波动幅度随土层深度的增加同样减小。随土层深度增加，平均相对偏差及其标准差的波动幅度都减小，表明土壤水分时间稳定性随土层深度增加而增强，这与许多学者的研究结果一致[19-20]。

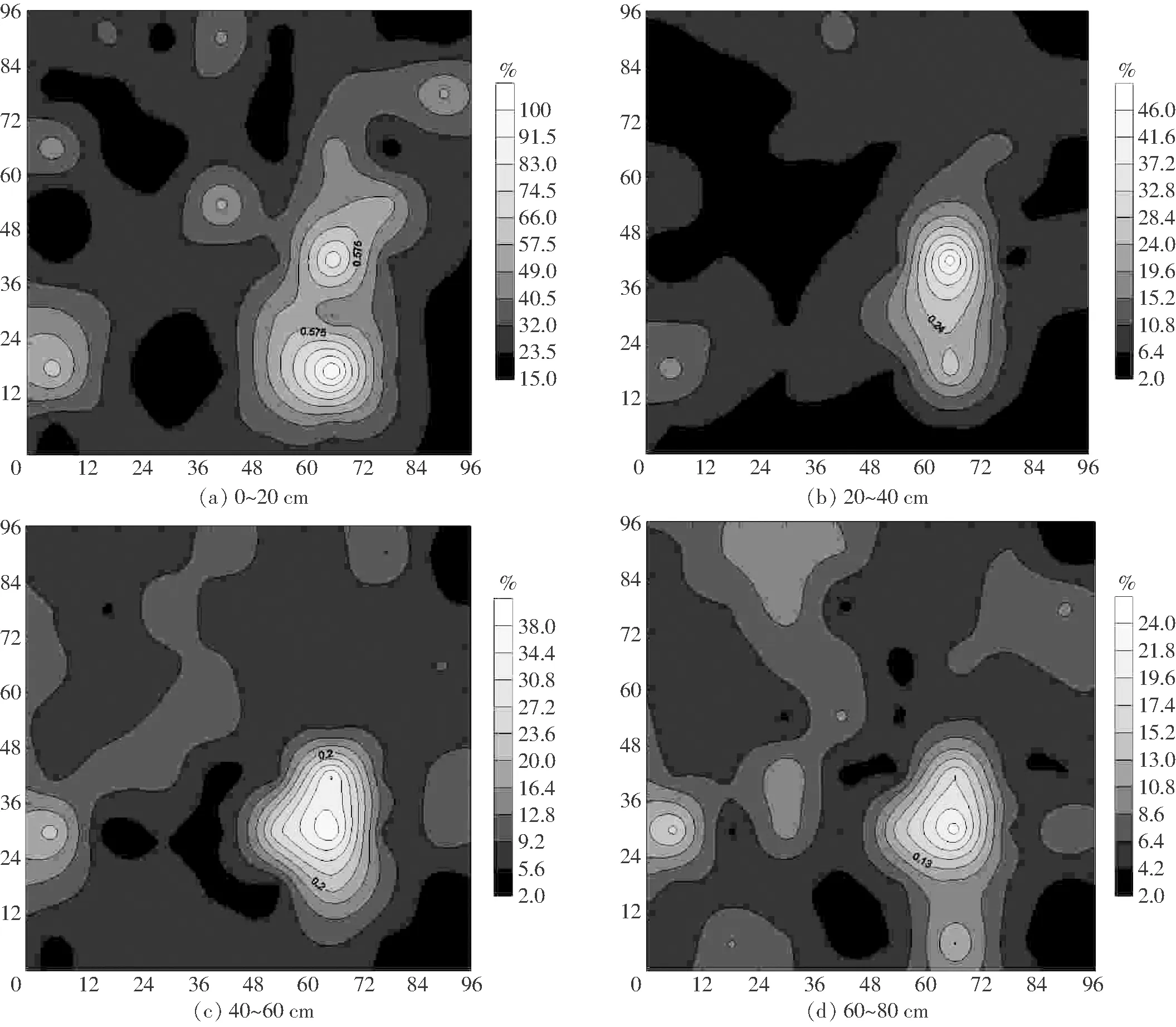
图3 土壤含水率平均相对偏差标准差等值线图Fig.3 Contour maps of standard deviation of mean relative difference of soil water content

由表2可知，平均相对偏差与其标准差的相关系数分别为-0.114、0.022、0.543、0.416，两者相关性在0～20 cm和20～40 cm土层不显著，在40～60 cm和60～80 cm土层显著(0.01水平)。ZHANG等[21]发现平均相对偏差与其标准差有显著直线关系，朱绪超等[22]发现两者为二次曲线关系，不同学者得出的研究结果有所差异，可能与土壤类型、土层深度、覆盖植被、降雨和灌溉等因素不同有关。

基于式(2)和式(3)确定代表性测点的原则，反映不同土层土壤最低含水率的代表性测点分别是测点9、测点36、测点33、测点10，反映最高含水率的代表性测点分别是测点64、测点64、测点9、测点9，反映平均含水率的代表性测点分别是测点53、测点35、测点18、测点64，反映最不稳定的代表性测点分别是测点14、测点30、测点22、测点22，随土层深度增加，土壤最低含水率、最高含水率、平均含水率和最不稳定代表性测点均有所差异，主要是由于土层深度不同，影响土壤水分的因素不同而导致的，有必要对影响不同土层时间稳定性的因素进行深入研究。利用代表性测点可确定研究区域土壤的最低含水率、最高含水率和平均含水率等信息，为研究区土壤水分的调控和管理提供理论依据与指导。

2.3 秸秆还田条件下土壤水分时间稳定性与玉米穗质量的相关性分析

土壤水分是作物生长发育的一个重要因素，目前关于土壤水分时间稳定性与作物关系的研究很少。作物产量是反映作物生长状况的一个综合指标，为此本文分析了时间稳定性与玉米穗粒质量、穗轴质量的相互关系。由表3可知，单一尺度上，除40～60 cm土层平均相对偏差标准差与穗粒质量的相关性在0.05水平上显著外，其他土层平均相对偏差标准差与穗粒质量、穗轴质量的相关性均不显著；随土层深度增加，平均相对偏差标准差与穗粒质量、穗轴质量的相关程度均未呈现规律性变化趋势。

表2 土壤含水率平均相对偏差与其标准差的相关系数Tab.2 Correlation coefficient between mean relative difference and standard deviation of soil water content

注：** 表示在p<0.01水平上显著，下同。

注：*表示在p<0.05水平上显著，下同；σ20、σ40、σ60、σ80表示0～20 cm、20～40 cm、40～60 cm、60～80 cm土层土壤含水率平均相对偏差标准差，WL、WZ表示玉米穗粒质量和穗轴质量。

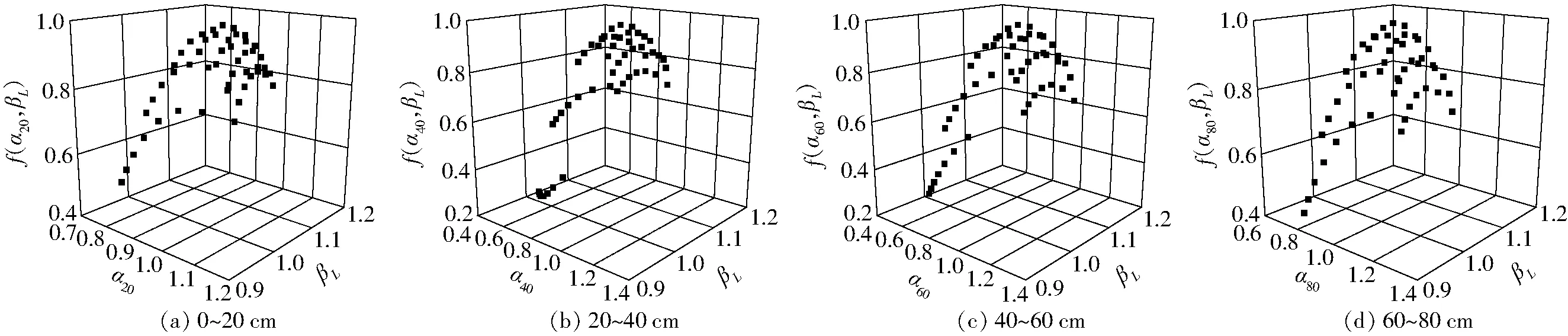
图4 土壤含水率平均相对偏差标准差与穗粒质量的联合多重分形谱Fig.4 Joint multi-fractal spectra of standard deviation of mean relative difference of soil water content and grain weight per ear

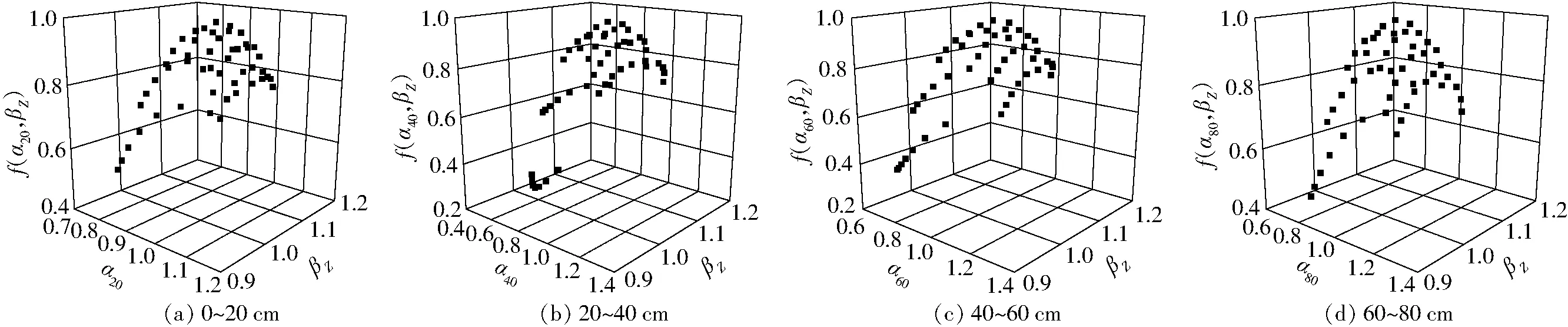
图5 土壤含水率平均相对偏差标准差与穗轴质量的联合多重分形谱Fig.5 Joint multi-fractal spectra of standard deviation of mean relative difference of soil water content and axis weight per ear

不同尺度上主要影响因素或同一因素的影响程度不一定相同，单一尺度相关性分析不一定能完整地揭示出研究对象之间的相互关系，多尺度相关性分析能更深入地揭示研究对象之间的相互关系，在这一方面已开展了许多研究[23-25]。为此，利用联合多重分形理论研究了土壤水分时间稳定性与玉米穗粒质量、穗轴质量的多尺度相关性。图4和图5分别为时间稳定性与穗粒质量、穗轴质量的联合多重分形谱，α20、α40、α60、α80分别表示0～20 cm、20～40 cm、40～60 cm、60～80 cm土层平均相对偏差标准差的联合奇异指数，βL、βZ分别表示穗粒质量、穗轴质量的联合奇异指数。从图4和图5可以看出，不同土层平均相对偏差标准差与穗粒质量、穗轴质量的联合多重分形谱均有所差异。为量化时间稳定性与穗粒质量、穗轴质量的多尺度相关性，计算了平均相对偏差标准差与穗粒质量、穗轴质量联合奇异指数的相关性(表4)。由表4可知，0～20 cm、20～40 cm土层平均相对偏差标准差与穗粒质量联合奇异指数的相关性不显著，40～60 cm、60～80 cm土层两者联合奇异指数的相关性分别在0.01和0.05水平上显著，与单一尺度上得出的结论有所差异；不同土层平均相对偏差标准差与穗轴质量联合奇异指数的相关性均不显著，与单一尺度上得出的结论一致；随土层深度增加，平均相对偏差标准差与穗粒质量、穗轴质量联合奇异指数的相关程度均先增后降，与单一尺度上得出的结论不同；除0～20 cm土层平均相对偏差标准差与穗轴质量的多尺度相关程度小于单一尺度相关程度外，其他土层两者的多尺度相关程度均大于单一尺度相关程度。基于土壤水分时间稳定性与穗质量的多尺度相关特征，一方面能够深入了解土壤水分对作物的影响机制，另一方面通过合理的估算、管理与调控农田不同土层土壤水分，能够促进作物产量的提高。

表4 土壤含水率平均相对偏差标准差与玉米穗质量联合奇异指数的相关系数Tab.4 Correlation coefficient between joint singularity exponents for standard deviation of mean relative difference of soil water content and corn ear weight

3 结论

(1)研究区土壤水分时间稳定性随着土层深度增加而增强，且较深土层(40～60 cm、60～80 cm)土壤水分时间稳定性的空间分布特征比较相似；0～20 cm、20～40 cm土层土壤水分时间稳定性与土壤含水率的相关性不显著，40～60 cm、60～80 cm土层土壤含水率较高的测点时间稳定性较强；土层深度不同，土壤水分代表性测点有所差异，利用代表性测点可确定研究区域土壤最低含水率、最高含水率和平均含水率等信息，可为农田土壤水分估算与管理提供理论依据。

(2)单一尺度和多尺度上，时间稳定性与穗轴质量的相关程度均不显著，与穗粒质量相关程度的显著性随土层深度不同有所差异，与穗粒质量、穗轴质量的相关程度随土层深度的变化趋势不同；大部分土层土壤水分时间稳定性与穗粒质量、穗轴质量的多尺度相关程度均大于单一尺度相关程度。多尺度分析能更深入确定时间稳定性与玉米穗质量的相互关系，为进一步揭示土壤水分对作物的影响提供理论依据。