先进磁镜装置中径向电场对高能粒子的约束性能研究*

石黎铭 吴雪科 万迪 李会东† 樊群超‡ 王中天 冯灏 王占辉 马杰

1)(西华大学理学院,高性能科学计算省高校重点实验室,成都 610039)

2)(山西大学量子光学与光量子国家重点实验室,太原 030006)

1 引 言

尽管托卡马克被认为是未来最具有实用价值的磁约束聚变装置,但其聚变β值较低、经济效益不明显,且实现可控核聚变反应至今还有很多技术难题未得到很好的解决.具有较高β值的类磁镜聚变反应装置在经济和效率上更具优势[1,2].串节磁镜[3]、反场箍缩(reversed field pinch,RFP)[4]和场反位形(field reversed configuration,FRC)[5-7]等类磁镜结构聚变反应装置作为实现聚变能源商业化的一支潜在力量引起了世界上不少科学家的研究兴趣[1,3,8].

近年来,串节磁镜装置KMAX、多势阱装置EMC2、RFP等类磁镜装置在约束高温等离子体方面取得了很大进展[3-14].紧凑型聚变反应装置(compact fusion reactor,CFR)是由洛克希德马丁(Lockheed Martin)公司根据“磁镜约束”原理提出的一种“高β聚变反应堆”,其体积较小,具有较大的潜在应用价值.CFR装置由多个线圈构成(图1),中性束由加热装置注入,约束磁场由多组同轴电流线圈产生,分别是一个中心线圈,一组内部线圈,两组封装线圈和一组磁镜线圈,各组线圈的半径大小、位置、电流强度以及线圈数量均可根据需求适当调节.装置内部线圈的电流方向与其他几组线圈电流方向相反,在装置内形成会切磁场位形,构成了一个边界附近磁场较强而芯部磁场较弱的磁阱结构,使高温等离子体能够较好地约束在装置内部[14].当轴心附近的带电粒子向外运动时,周围的强磁场就会再把它推回来.尽管一开始这种作用力很小,但是粒子偏离轴心越远,周围磁场的推力就会越大[14].最新的T4B实验结果表明,CFR装置中的等离子体在高β值条件下具有稳定的膨胀率；零维约束模型预测结果表明,在T4B装置中可以通过中性He粒子束在加热条件下所发生的电荷交换反应向等离子体传递能量,加热等离子体,使等离子体获得毫秒量级的良好约束,同时装置内会产生高能电子和He离子[15].CFR装置内高能粒子的鞘层损失和轴向尖端损失对高温等离子体的约束具有重要影响,研究这些高能粒子的约束性能具有重要的实际意义[16].

图1 Lockheed Martin紧凑型聚变反应磁镜装置 (a)构造；(b)等离子体分布Fig.1.(a)The structure of CFR machine；(b)plasma distribution in CFR (https：//en.wikipedia.org/wiki/Lockheed_Martin_Compact_Fusion_Reactor).

径向电场Er在磁约束聚变等离子体的研究中具有重要作用[17-23].1982年在ASDEX托卡马克磁约束聚变中首次发现径向电场在L模到H模转化过程中的关键性作用,径向电场的突然变化引起了L模到H模的转化,从而抑制了湍流波动,由反常输运过程控制的等离子体约束在H模下得到了改善[17-19].近年来,有关径向电场的研究得到了迅速发展：理论研究表明径向电场在形成输运垒和L-H转换机制中可能起着决定性作用[20],实验上也证实了径向电场和转换机制的存在[21].此外,径向电场对托卡马克等离子体中粒子的“香蕉”轨道中心漂移、粒子轨道和损失锥边界等都会产生影响,径向电场对粒子轨道的改变会进一步影响等离子体输运[22,23].在托卡马克装置中,可以采用在等离子体边界区域安装偏压电极改善粒子和能量约束.1989年,最早在CCT托卡马克装置中实现了偏压实验,随后在J-TEXT、ISTTOK托卡马克等装置上都进行了偏压实验,结果表明偏压电极可以有效地提高径向电场和等离子体约束性能[24-25].在类磁镜装置中径向电场会影响粒子平行磁力线方向的运动速度,使得带电粒子加速或减速,从而达到改善高能粒子约束性能的目的.因此,在CFR等线性装置中可以通过末端加偏压电极形成电场来改善等离子体的约束性能,这在KMAX等线性装置中已得到有效验证[26].

目前已有大量的数值研究工作讨论了粒子约束的相关问题[27-29].与多粒子模拟、磁流体描述、统计描述等其他模拟方法相比,单粒子模拟能够更加清晰地分析装置中粒子运动的特点和轨道的拓扑结构,为研究高能粒子、粒子输运等提供理论基础支撑[30].本文采用Boris算法[31-36]对单粒子进行模拟,研究在径向电场作用下CFR装置中粒子的运动轨道,并比较不同径向电场作用对粒子约束性能的影响.第2节详细介绍CFR磁场位形的计算和单粒子模拟方法,并研究粒子轨道特性；第3节研究径向电场Er对CFR中高能α粒子损失率的影响；第4节总结.

2 理论方法

2.1 CFR磁场位形的计算

在柱坐标系(r,θ,z)中,对于以Z轴为中心的电流环,由毕奥-萨伐尔定律可知径向位置r和轴向位置z处产生的磁场分别为：

其中µ0为磁导率,a为电流线圈的半径,I为电流线圈中的电流,K(k2)和E(k2)分别为第一类椭圆积分和第二类椭圆积分.

表1 CFR装置线圈参数Table 1.Main parameters of coils in CFR.

本文研究的CFR装置由9个半径不同的共轴电流线圈组成,总磁场在径向r和轴向z的分量表示为：

其中,a(n)为第n个电流线圈的半径,I(n)为其中的电流,d(n)为第n个电流线圈所处的z轴位置,此时

CFR装置中各线圈所处的轴向位置、线圈中半径、线圈中所通电流的大小和方向如表1所列[14].

图2 CFR装置中R-Z平面上的磁场位形Fig.2.The magnetic flux of the R-Z plane in the CFR machine.

根据(3)式和(4)式以及表1中的数据编程计算出CFR装置中磁场分布如图2所示.从图中可以看出,在装置的边缘区域磁场较强,而芯部磁场较弱,整个装置的内部形成了较好的磁镜位形,在该装置的内部可以约束β值较高的高温等离子体.

2.2 单粒子轨道演化方程

CFR装置中,可以通过以下运动方程来演化高能带电粒子的运动轨迹：

其中B为磁场强度,E为电场强度.在矢量方程(5)式和(6)式的数值求解过程中,针对因数值误差的累积而造成的粒子能量衰减,从而导致轨道失真的问题,本文使用了目前比较流行的Boris算法.

Boris算法通过第k步相空间坐标(xk,vk)求解第k+1步相空间坐标(xk+1,vk+1).(5)式和(6)式可写为如下离散格式：

其中h为时间步长,tk=kh,Boris算法将电场力和磁场力分开计算,通过(9)式和(10)式可从vk解析计算得到

从第k步递推到第k+1步,电场力驱动的一半首先作用在vk上获得v¯,再通过(10)式计算得到v+,进一步将电场力驱动的一半加在v+上获得vk+1.最终通过(11)式获得vk+1.矩阵形式的Boris 算法可表示为

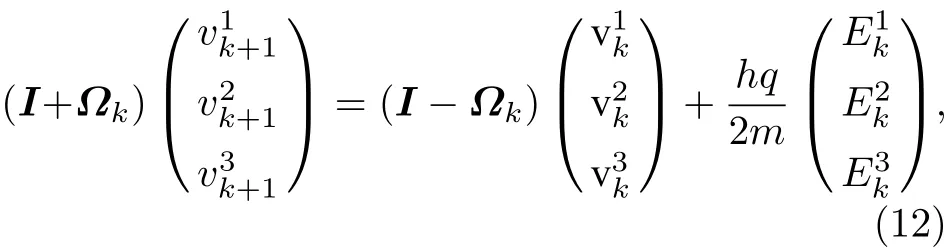
其中I是单位矩阵,Ωk的表达式为

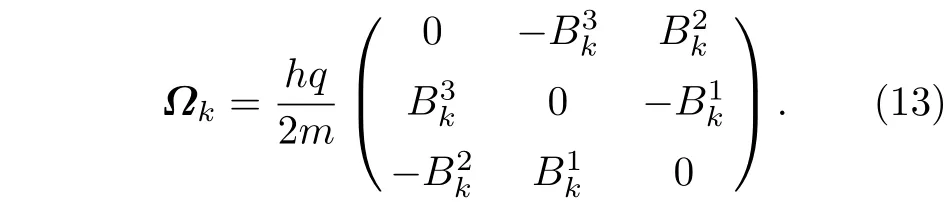
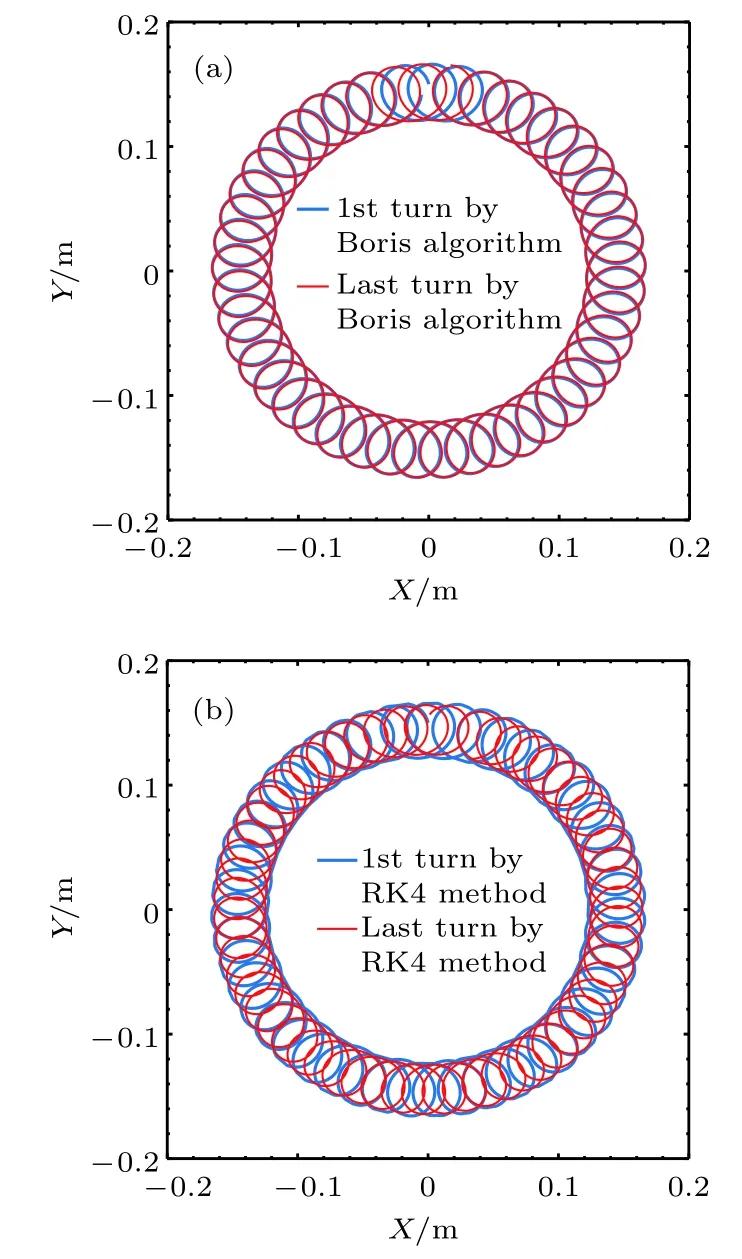
图3 Boris 算法和RK4算法模拟下第一个漂移周期和最后一个漂移周期的轨道(模拟时间1200 μs)(a)Boris 算法；(b)RK4算法Fig.3.Orbits of the first and the last drift motion periods by the Boris algorithm and the RK4 algorithm (simulation time is 1200 μs)：(a)The Boris algorithm；(b)the RK4 algorithm.

在CFR磁场位形中,由Boris算法计算得到的能量误差和轨道失真度较小.在CFR装置中,为验证方法的优越性,假定粒子位于只有z方向磁场的轴向z0=0 和径向r0/a=0.15 处的位置上.给定粒子的初始速度与z轴垂直,φ0=0.5π.在验证时间步长收敛性的前提下,取时间步长h为拉莫尔回旋周期的1/30.运行时间为1200 μs (约200个漂移周期),并设电场强度为2 kV/m,由原点沿半径向外.在该磁场平面内,带电粒子受到磁场力的作用进行拉莫尔回旋运动.由于电场、磁场梯度和磁场曲率的存在,带电粒子会发生E×B漂移、磁场梯度漂移和磁场曲率漂移,漂移方向均沿着极向方向.图3(a)和图3(b)分别为Boris算法和四阶龙格-库塔RK4算法模拟得到的导心轨迹半径约为0.15的粒子在第一个漂移周期和最后一个周期的轨道图,圆环厚度近似为粒子拉莫尔回旋半径长度.模拟结果表明,长时间迭代计算后Boris算法仍能保持轨道形状不发生改变,与物理实际一致.RK4算法下的轨道形状发生了改变,且完成最后一个周期需要更多的计算步数,数值误差较大.图4中分别计算了Boris算法和四阶龙格-库塔RK4算法的相对能量误差随时间的变化情况.研究结果表明,Boris算法在无电场情况下能够保证粒子的能量绝对守恒,而RK4算法的数值误差随模拟时间的积累不断增大.

图4 Boris算法和RK4算法数相对能量误差随时间变化对比Fig.4.Comparison of the relative energy errors between Boris method and RK4 method.

3 数值模拟结果及分析

3.1 径向电场对α粒子轨道的影响

在径向电场作用下,通过数值求解(5)式和(6)式模拟获得了α粒子的运动轨迹.模拟采用T4B参数[15],装置直径为1 m,长2 m.功率为1 MW,在注入的中性束中,He粒子能量为25 keV.因此,本文模拟将粒子选定为能量为25 keV的α粒子.在模拟α粒子轨道的过程中,将粒子置于轴向位置z0=0 和径向位置r0/a=0.4 处,此处磁场B0=5T,设定粒子的初始速度与Z轴的夹角φ0=0.5π,粒子的极向初始速度vϑ0=0.2vt,其中vt为粒子的热速度,粒子的平行速度和垂直速度之比v‖/v⊥=1 .在CFR装置中,将α粒子能量设定为25 keV,通过设置不同的径向电场Er(—2 kV/m,0,+2 kV/m)研究α粒子轨道情况.如图5所示,三种不同颜色的轨迹分别表示在无电场作用、负向径向电场(方向指向轴心)和正向径向电场作用下α粒子运动500 μs的轨道.研究表明,径向电场Er会对粒子漂移速度产生影响,在正向径向电场作用下,粒子漂移速度增大,α粒子反弹点向中心线圈位置移动；而在负向径向电场作用下,粒子漂移速度减小,α粒子反弹点向两端磁镜线圈位置移动.

图5 (a)CFR粒子轨道；(b)粒子轨道在X-Y截面的投影；(c)粒子轨道在R-Z截面的投影Fig.5.(a)The orbit of particles in CFR；(b)the projection of the particle orbital in the X-Y plane；(c)the projection of the particle orbital in the R-Z plane.

根据能量守恒,平行于磁场的速度v‖在径向电场作用后可表示为

其中W为粒子总能量,m为粒子质量,µM为磁矩,qα为α粒子电荷,Φ为电场电势.(14)式中总能量W、电荷qα、质量m和磁矩µM均为常量.从(14)式可知,当粒子沿磁力线运动时,径向电场会影响粒子平行磁力线方向的速度v‖,电势越大,v‖越小,粒子沿Z向运动的距离越短,更不容易沿轴向尖端损失.

粒子在CFR中的漂移是由磁场的梯度漂移、磁场曲率漂移和电漂移共同产生的,粒子的速度可以表示为[37]

其中,ωc为回旋频率,Rc为曲率矢量半径,v‖,v⊥分别代表平行和垂直于磁场方向的速度,(15)式右边第一项表示平行磁场的分量,第二项是磁场不均匀引起的总漂移,第三项是电漂移.

在正向电场作用下,电漂移引起的漂移速度和磁场不均匀引起的总漂移速度方向一致,导致粒子极向速度增大,平行于磁场方向的速度减小,有效地降低了粒子轴向尖端损失.而在负向电场作用下,电漂移引起的漂移速度和磁场不均匀引起的总漂移方向相反,此时径向电场引起的电漂移和磁场梯度及曲率引起的总漂移存在竞争关系.在负向电场情况下,当由磁场不均匀引起的漂移起主导作用时,粒子总漂移速度减小,平行于磁场方向的速度增加；但当负向径向电场增大到一定程度时,电漂移将超过磁场漂移逐渐起主导作用,粒子总漂移速度将增加.

3.2 绝热区粒子模拟

在CFR装置中心区域,由封装的线会切以及两个纺锤形的会切形成了一个磁势阱结构,芯部区域的磁场趋于零,该结构产生一个临界磁面,将整个磁场位形分为绝热区和非绝热区.在CFR装置芯部附近磁场较弱,磁场梯度和曲率较大,类似于会切位形,该区域内磁矩不守恒,可称为非绝热区；而其他区域磁矩守恒,称为绝热区[16].根据紧凑型先进磁镜系统的磁场位形分布特点容易看出,绝热区粒子更容易沿轴向尖端损失,当高能粒子的初始速度与磁场平行时,粒子约束性最差,粒子极容易通过磁镜的端口而损失.选取在绝热区最容易损失的能量为25 keV的α粒子进行模拟.模拟过程中设定时间步长Δt= 1×10—12s,z0=0,φ0=0,粒子的极向初始速度vϑ0=0,在r0/a=0.2—0.5 范围内,径向每隔0.05的长度取一个径向点.当v‖/v=1,即初始速度与磁场方向平行时,粒子极容易沿着磁力线从端口逃离装置.在当前粒子初始条件下,α粒子仅仅运动了2.354 μs便全部直接损失(如图6所示).

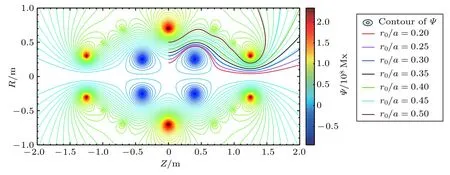
图6 CFR中α粒子损失轨道Fig.6.The lost orbits of theαparticles in CFR.

为了研究在绝热区不同径向位置处径向电场对能量为25 keV的α粒子最易损失方向(平行于Z轴方向)约束性能的影响,将粒子初始条件设置为z0=0,φ0=0,vϑ0=0 和v‖/v=1,在r0/a=0.2— 0.5范围内,径向每隔0.05的长度取一个径向点,在同一个径向位置,通过不断调整正向径向电场的大小研究粒子约束性能的变化.研究表明,在没有径向电场存在的情况下,能量为25 keV的α粒子只能在装置中停留几个微秒(如图6).随着正向径向电场的增强,粒子在装置内的约束时间不断增长,当正向电场增大到某一临界值时,在最容易损失位置处注入的α粒子轨道将会长时间停留在装置内部而不是逃离装置,粒子能够很好地约束在磁镜内Z处于—1.15—1.15之间(如图7).在模拟中,选定不同的径向初始位置,分析粒子在不同径向电场作用下的运动轨迹得到了相同的结果.图8中给出了在r0/a=0.3 处,不同径向电场作用下α粒子的运动轨迹,由图可见,当正向电场由58620 V/m增大到58621 V/m时,粒子能够被长时间地约束在CFR装置内,说明了正向径向电场的存在可以改善粒子约束性能.数值计算的结果表明,不同径向位置处使得粒子能够长时间约束的径向电场临界值与粒子的初始条件有关：粒子初始位置越靠近轴心位置(r= 0),正向的径向电场临界值越大.当径向电场大于临界场值,在绝热区运动的α粒子都能被很好地约束在CFR装置内,区域内粒子损失率将降至最低,甚至能将所有粒子约束.

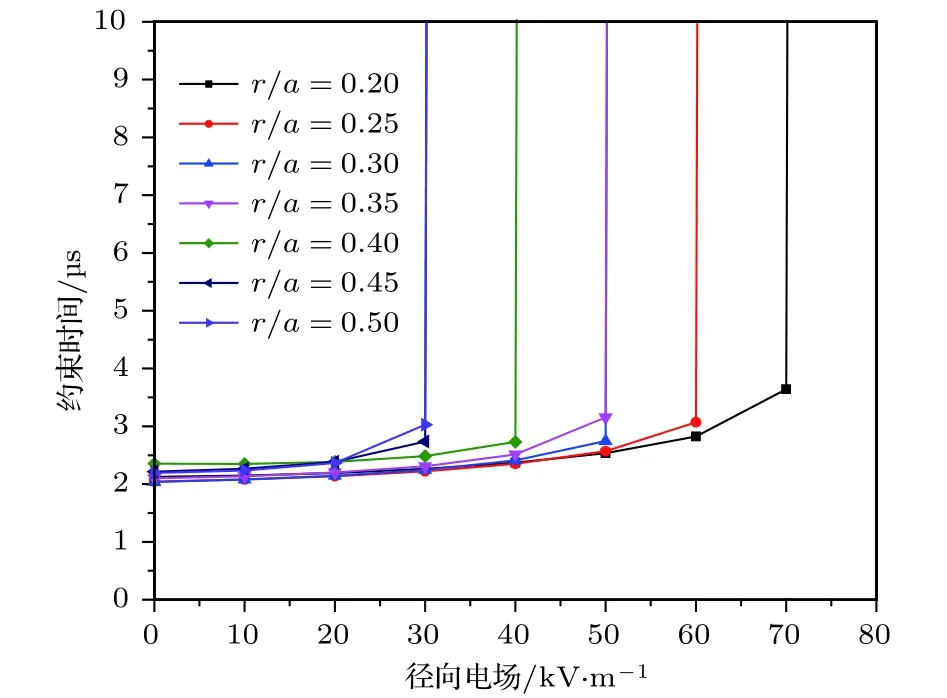
图7 粒子约束时间随着正向电场强度的变化Fig.7.The particle confinement time changes with the intensity of the positive electric field.

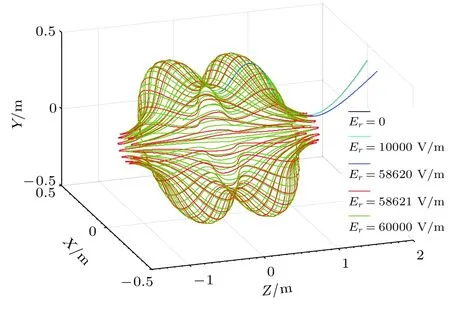
图8 初始位置 r0/a=0.3 处α粒子在不同正向径向电场作用下的运动轨迹Fig.8.The orbits of α particle under the different positive radial electric fields at r0/a=0.3 .

同时研究了负向径向电场对能量为25 keV的α粒子约束性能的影响,研究过程中选取粒子的初始状态与正向电场情况下相同.研究表明,负向径向电场的存在同样可以改善粒子的约束性能.然而,负向径向电场对粒子约束性能的影响随着电场强度的增加,在所有位置的约束时间并未表现出都是单调递增的趋势：在负向电场强度比较小时,粒子的约束时间随电场强度的增大而减小,表明此时电场使粒子更容易损失；而当电场强度增大到一定程度时,在最容易损失位置注入的α粒子却能够很好地约束在CFR装置内(如图9和图10).

以上分析了在极限情况下,最容易损失的粒子通过外加径向电场得到了很好的约束.为了更直观地探究径向电场对绝热区无碰撞α粒子损失率的影响,选取初始条件为z0=0,φ0=0,vϑ0=0.2vt,使粒子连续分布在径向初始位置r0/a= (0.2—0.5)之间,以不同的入射角(0-2π)发射500个α粒子,得到粒子运行500 μs后的损失率(如图11所示).研究结果表明,对于绝热区运动的高能粒子,随着正向径向电场增大,粒子损失率降低.而在负向径向电场作用下,随着电场强度增大,粒子损失率先增大后减小.尽管将高能α粒子全部约束在CFR装置中需要提供极大的径向电场,但在电极偏压装置可控的径向电场下已经能够有效地改善粒子损失,提高粒子约束性.

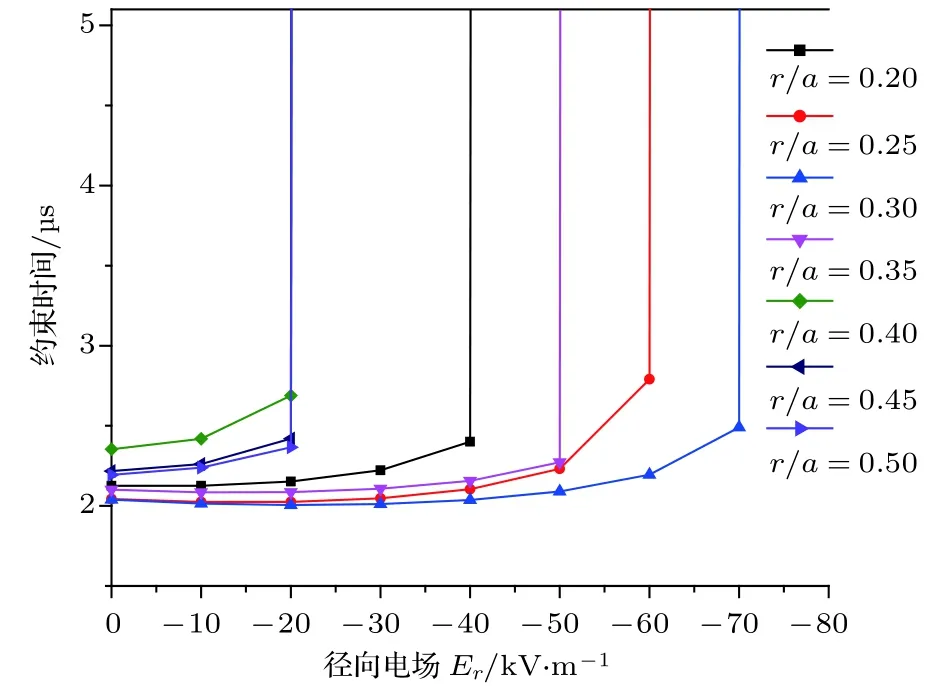
图9 粒子约束时间随着负向径向电场强度的变化Fig.9.The variations of particle confinement time with the intensity of the negative radial electric field.

图10 初始位置 处α粒子在不同负向径向电场作用下的轨道r0/a=0.3Fig.10.The orbits of α particle under the different negative radial electric fields at .r0/a=0.3

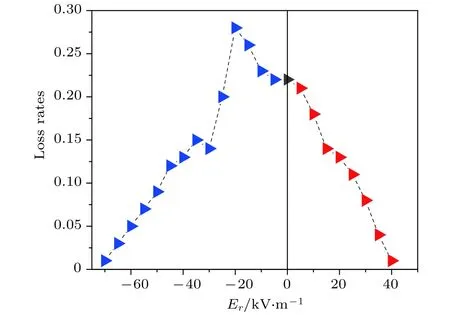
图11 不同径向电场作用下的α粒子损失率Fig.11.The loss rates of the α particles with different radial electric fields.

4 结 论

径向电场的存在会改变装置内带电粒子平行磁力线方向的速度,对装置内高能粒子的约束产生影响.本文从牛顿运动方程出发,运用Boris算法模拟α粒子在CFR装置中的运动轨道,探究了不同径向电场作用下α粒子在CFR绝热区约束性能的差异.模拟发现：在正向径向电场作用下,α粒子运动电漂移速度与磁场梯度和曲率引起的漂移存在竞争,α粒子运动轨道反弹点沿磁力线向径向电场方向移动.随着电场强度增大,α粒子在CFR中约束性变好,当径向电场强度达到一定临界值时,即使最容易损失的α粒子也能够很好地约束在装置内；在负向径向电场作用下,α粒子漂移速度增大.随着电场强度的不断增大,初始速度平行于Z轴方向的极容易损失的α粒子在CFR中约束时间先减少,但当电场强度达到某一特定值时,粒子约束时间不断增加,从而很好地约束在CFR装置内部.在CFR装置中,当所施加的电场强度增大到一定临界值时,粒子能够长时间地约束在装置内部,约束时间可以达到与当前托卡马克装置粒子约束时间相当的毫秒量级.由于在CFR装置内的磁场使用的是最优化磁场位形,装置内部的高能粒子可以达到毫秒量级约束时间,然而该类线性装置较托卡马克装置具有约束效率(β值)更高、尺寸更小和造价更低等诸多优点,在未来的磁约束聚变领域具有较好的应用前景.