毛乌素沙地南缘降水入渗滞后补给与模型参数敏感性分析

王 锴, 杨泽元, 袁 悦, 陈志军

(1.长安大学 环境科学与工程学院, 陕西 西安 710054; 2.旱区地下水文与生态效应教育部重点实验室,陕西 西安 710054; 3.陕西省地下水与生态环境工程研究中心, 陕西 西安 710054)

毛乌素沙地位于半干旱气候区，境内包含陕北和内蒙能源化工基地，随着该地区工农业发展与人口增长，用水量短缺形势越发严峻。该地区主要用水来源为地下水，降水入渗是地下水补给的主要来源，研究该地区降水入渗补给是其地下水资源评价的重要基础工作[1]。前人[2-3]常采用年降水量与区域入渗补给系数计算区域性降水入渗补给量，很少考虑入渗过程的滞后性。地下水补给总是滞后于降水事件，某一时段内补给量实际由该时段之前的时段内降水所决定。同时，由于补给滞后的存在，含水层对于人类活动与气候变化的响应往往不会立即发生[4]，这给地下水可持续开发带来挑战。因此研究地下水的补给滞后现象对于提升地下水资源评价精度与地下水资源合理利用具有重要意义。

1 材料与方法

1.1 研究区概况

研究区位于陕西省榆林市补浪河乡，地处毛乌素沙地南缘。年均降水量365 mm，年均蒸发量1 246 mm。主要潜水含水层为第四系风积孔隙含水层，岩性为中砂，不含黏土(表1)。地下水常年埋深1.3～1.5 m，主要补给来源为大气降水，占天然补给总量85%以上[16]，主要排泄去路为蒸发排泄。

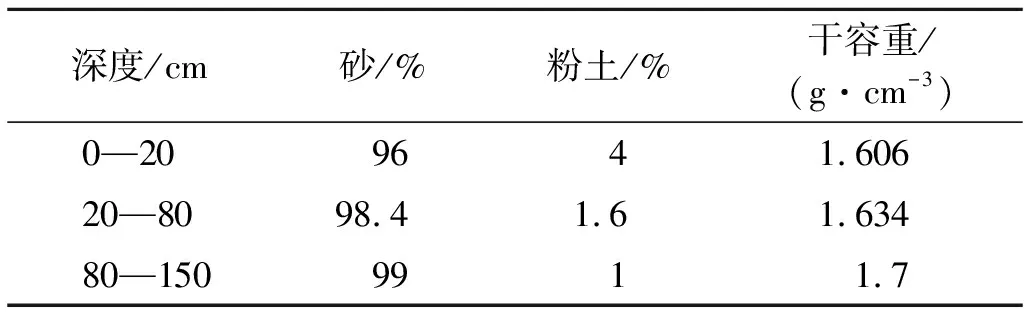
表1 研究区不同层土壤质地

1.2 研究方法

在原国土资源部地下水与生态陕西榆林野外观测基地建立原位试验场。监测地下5，10，30，60，90 cm深处含水率，同时获取场地气象数据。包气带含水率和温度由5 TM传感器监测(美国Decagon公司)，采集频率为10 min。气象数据由试验场内的波纹比系统(05130-5RMYong，美国Campbell公司)自动监测。地下水位由MiniDiver自动监测并记录数据，气象数据和地下水位的采集频率均为1 h。

以野外原位监测数据为基础研究场地内包气带含水率与地下水位对降水入渗的滞后响应。根据场地条件建立水文地质概念模型并利用Hydrus-1D软件建立降水入渗模型。采用野外监测数据进行模型参数的识别与优化。

采用相对平均误差(AVRE)、相关系数(R)作为指标进行识别期模型误差分析。

AVRE=∑(VC1/VO1)/n

(1)

(2)

式中：VCi——模拟值； VOi——原位观测值；n——数据总数量。

通过上述过程识别获取基本参数，基于原位监测含水率，负压，温度数据建立反解模型(共14 d，4 695个数据点)。反解计算采用Hydrus-1D的Inverse solution模块进行，对van-Genuchten方程中的各参数θr(残余含水率)，α,n(水土特征曲线方程的参数)和Ks(饱和渗透系数)进行反解，反解方法为最小目标函数法[17]。选取SSR，r2最优对应的参数作为参数优化结果。其中SSR为反解过程中目标函数值。r2为拟合值与观测值的相关系数，r2为1表示拟合最佳。

(3)

注意到,热带西北太平洋位于东亚季风区,而热带东南印度洋位于南亚季风区以南(Wang and Linho,2002),环流结构有所不同。同时,在气候学上夏季位于对流层低层起自索马里至西太平洋热带地区的西风气流和对流层上层的东风气流将西太平洋热带地区与热带印度洋地区联系起来。对印度洋与太平洋上环流变化联系的研究仅限于赤道或近赤道的纬向区域,其联系的重要纽带是Walker环流,而对于赤道外地区两大洋上空环流变化的联系却未能有较好的研究。那么,位于海洋性大陆东南边缘和西北边缘的两个地区上的环流变化是否存在联系呢?这种联系是否存在年代际变化呢?其原因是什么呢?本文将回答这些问题。

参数获取完毕后，以累计底部通量为指标，采用单参数扰动方法进行敏感性分析，重点关注不同参数改变对于地下水补给滞后的影响。采用输入输出变化率(ROV)来分析模型计算对于参数的敏感性[15]。

(4)

式中：C(t)——模型实际计算结果(改变某一参数值的结果)；Cref(t)——模型参考计算结果(所有参数保持不变的结果)，此处计算结果均为累计底部通量；P——实际输入参数；Pref为参考输入参数；t——时间。ROV(t)的绝对值越大，则模型对该参数越敏感。由于介质被划为多层，因此输入输出变化率均采用各层平均值。

2 结果与分析

2.1 包气带含水率响应滞后

研究区降水年际变化大，降水主要集中在每年的6—9月份，为丰雨期。由于每年的11月至次年3月是该区的冰冻期，只发生少量降雪，研究时段确定为2014年3—10月并将时段内的降水依据国标划分为小雨、中雨、大雨与暴雨[18]。包气带深度越浅，降水后含水率响应越剧烈，部分降水事件中地表最大含水率甚至接近饱和；同一地下水埋深下，降水量越大，包气带响应深度越大。以8月26日至9月5日为例(图1)，8月27日降水0.82 cm(小雨)，仅5 cm深度有明显响应，其他深度含水率均无明显变化；8月30日降水7.1 cm(暴雨)，包气带所有深度含水率都明显上升。选取研究时段内主要降水事件，通过相关性分析研究降水量与入渗响应深度的关系。如图1所示，入渗响应深度与降水量呈显著线性相关，相关系数R为0.94>R(16，0.01)=0.59。随着包气带深度增加，含水率响应存在明显滞后；以7月8日降水为例，10 cm处滞后时间为13 h，30 cm为19 h，90 cm为29 h。

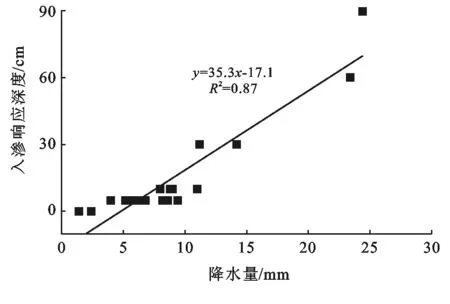
图1 入渗响应深度与降水量相关关系

注意到7月3日降水(降水量2.12 cm)历时4 h，最大雨强14 mm/h，5，10，30 cm深度含水率均明显响应，但90 cm处含水率只微弱变化；7月8日(降水量4.1 cm)历时27 h，最大雨强仅3 mm/h，90 cm处含水率明显上升。前者降水强度更大，后者降水量更大，这说明降水量对于响应深度的影响大于降水强度(图2)。

图2 降水量与含水率变化时间序列

2.2 地下水滞后补给

无降水的时段，地下水位保持相对稳定(图3)，小雨和中雨后地下水位均未响应，如6月25日降水5.2 mm，水位并无变化。大雨暴雨均会对地下水形成有效补给(如6月29日、7月3日、7月9日的降水)，使得地下水位上升。试验时段内对地下水形成有效补给的降水统计结果详见表2。从表2可知，降水量越大，地下水位上升幅度越大。相近降水事件如7月3日降水(降水量2.12 cm)与6月29日降水(共2.24 cm)下，水位埋深与地下水位升幅反相关。这是由于在蒸发条件相似时，水位埋深越大，包气带水分亏缺越大，降水后补给量也越小。降水之后，地下水位并不立即上升，一般把从降水开始到地下水位上升的时间间隔称为补给滞后时间；由表2可知，6月29日降水(共2.24 cm)补给滞后时间为4 h，7月3日降水(共2.12 cm)补给滞后时间为5 h；注意到这一滞后时间甚至小于30 cm处含水率响应时间，表明降水后存在优势流通道，降水入渗通过优势流通道提前进入地下水，引起地下水位响应。历次降水后地下水补给滞后时间均随着降水强度的增大而减小，但减小幅度逐渐放缓。这是由于随着降水强度的增大，入渗率也随之增大；但当降水强度逐渐接近或超过土壤入渗能力后，入渗率不再变化，相应的入渗补给滞后时间也趋于一定值。需要注意的是，9月10日降水3.06 cm，较9月22日降水5.46 cm差别并不大，但后者地下水位上升剧烈，这是由于后者的前期降水量更大，前期降水有效补给了包气带水分，较高的包气带含水率促进了后期降水入渗。

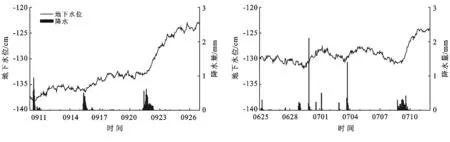
图3 地下水位与降水量变化时间序列

雨 型大 雨暴 雨降水量/mm21.241.430.671.654.622.4降水强度/(mm·h-1)4.241.531.717.92.14.48地下水位升幅/cm1.31.62.99.19.91.8补给滞后时间/h5118364 地下水埋深/cm雨前129.4129.5130.6145.3133.1121.6雨后128.1127.9127.7136.2123.2119.8

2.3 降水入渗数值模型建立与参数敏感性分析

2.3.1 模型建立 以地表为坐标原点，向上为正。建立水文地质概念模型，地表作为模型的上边界。地下埋深150 cm处作为模型的下边界，忽略水平径流，由此可以概化为变饱和带一维非稳定流模型。含水介质依据颗粒分析和容重概化为3层，其中0—20 cm为第1层，20—80 cm为第2层，80—150 cm为第3层。在Hydrus中选用大气边界作为水分运移的上边界条件，可变压力水头作为水分运移的下边界条件。热运移的上下边界条件分别为上下边界温度。选用Van-Genuchten方程作为水力特征曲线，考虑持水曲线的滞后效应。含水率初始条件采用与初始时间地下水位相平衡的含水率分布。温度初始条件设置为初始时刻监测值。模型的初始土壤水力学参数详见表3。采用Hydrus中基于颗粒分析和容重数据的神经网络预测结果。

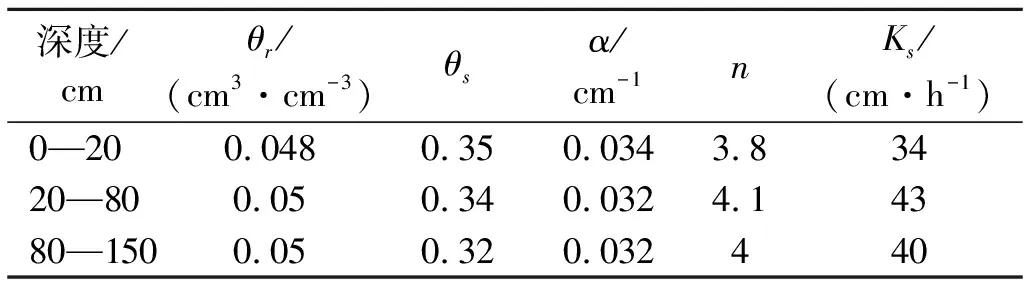
表3 经神经元预测分析得到的土壤水力学参数

注：θs，α，n,，Ks，θr均为van-Genuchten方程中参数。θr为残余含水率；α和n为水土特征曲线方程的参数；Ks为饱和渗透系数；θs为饱和含水率。

2.3.2 模型参数获取 选取2014年7月2—15日作为模型参数的识别期。识别期包气带深度5，30，60 cm处含水率、温度模拟值与观测值对比如图4所示。

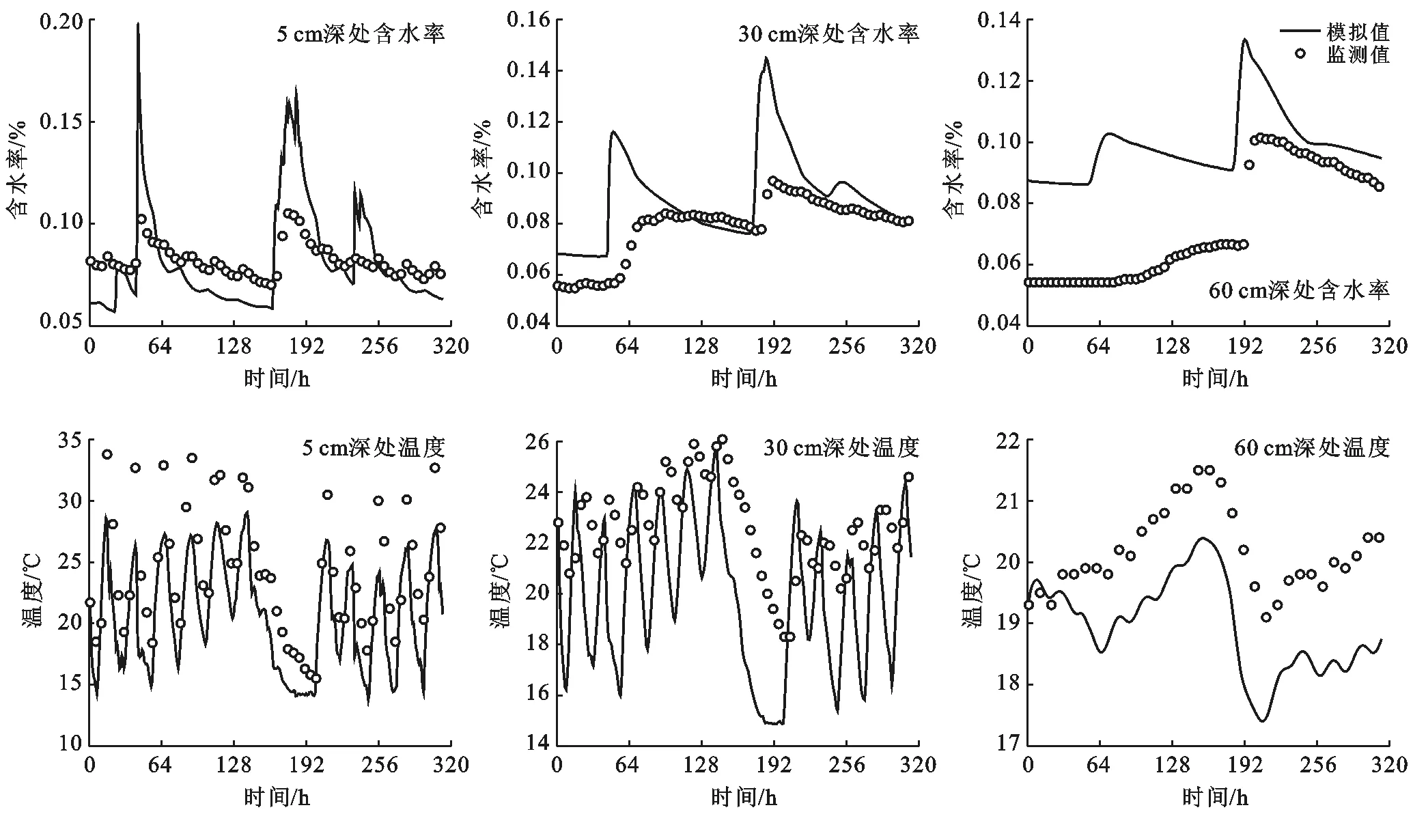
图4 模型识别期包气带不同深处含水率与温度

模型在识别期的计算误差结果详见表4—5，除埋深60 cm处误差较大外，总体计算结果较好。经过参数反演优化，选取SSR=1.854，r2=0.926时对应的参数作为优化结果，最终确定的水、热力学参数详见表6—7。

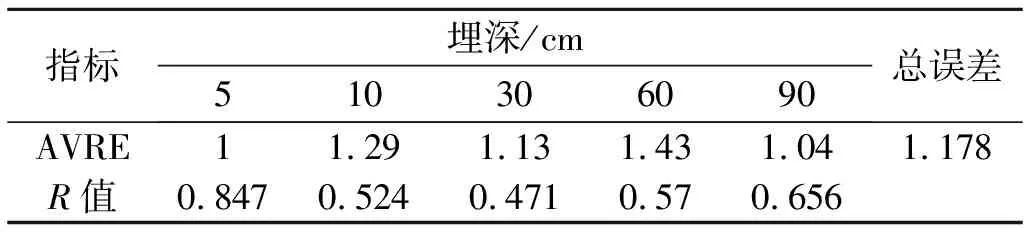
表4 识别期模型计算含水率误差结果

注： AVRE为模型计算值与监测值的相对平均误差，R为相关系数。

表5 识别期模型计算温度误差结果

2.3.3 van-Genuchten方程参数敏感性分析 由于调参过程中涉及的参数较多，对van-Genuchten主要的土壤水力学参数θr，α，n，Ks进行了敏感性分析。通过对某一参数进行增减，维持其余参数不变，确定参数敏感性[15]。敏感性分析中参数取用情况详见表8。

表6 模型识别及优化后所得土壤水力学参数

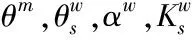
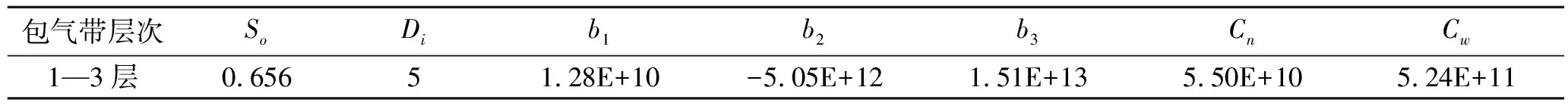
表7 模型识别及优化后所得土壤热力学参数

注：b1,b2,b3为热传导系数λ(θ)的参数；Cn为固态物质的体积热容；Cw为水的体积热容；Di为热扩散系数；So为固态物质体积百分比。

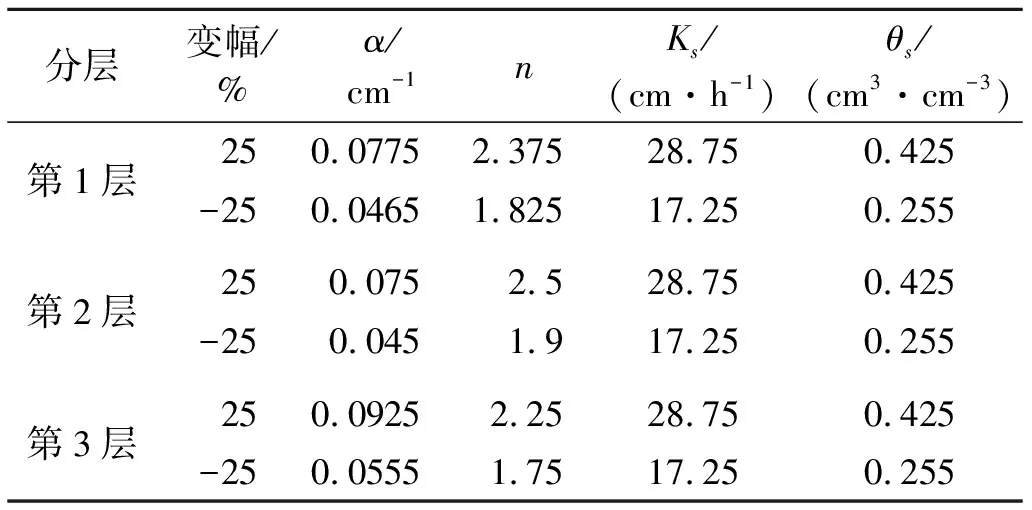
表8 参数敏感性分析中所用土壤水力学参数

注：考虑到n最小取1，故n的变化为在原始值与1作差的基础上再增减25%。

采用累积底部通量误差进行参数敏感性分析。时间起点为7月2日0：00，图中下标为0的表示该参数的初始值。-25表示减小25%的参数值，+25表示增加25%的参数值(图5)。各参数的输入输出变化率详见表9。从表9可知，底部通量对θs最为敏感，对Ks最不敏感。α与n的敏感性介于θs与Ks之间，其中n比α更敏感。若以底部通量代替地下水补给量，则地下水补给量的大小主要由θs控制，θs越大，入渗过程中包气带持水能力越强，地下水补给量越小。从图5中可以看出，θs与Ks对于降水补给的滞后影响较大，当Ks减小或θs增大时，累计底部通量拐点时间(指示着补给开始时间)明显滞后；其中θs增大25%，滞后时间增长10～16 h；Ks减小25%，滞后时间增长6～8 h。值得注意的是，若包气带剖面处于蒸发状态，Ks的改变几乎不引起底部通量的变化，此时Ks的敏感性很弱。

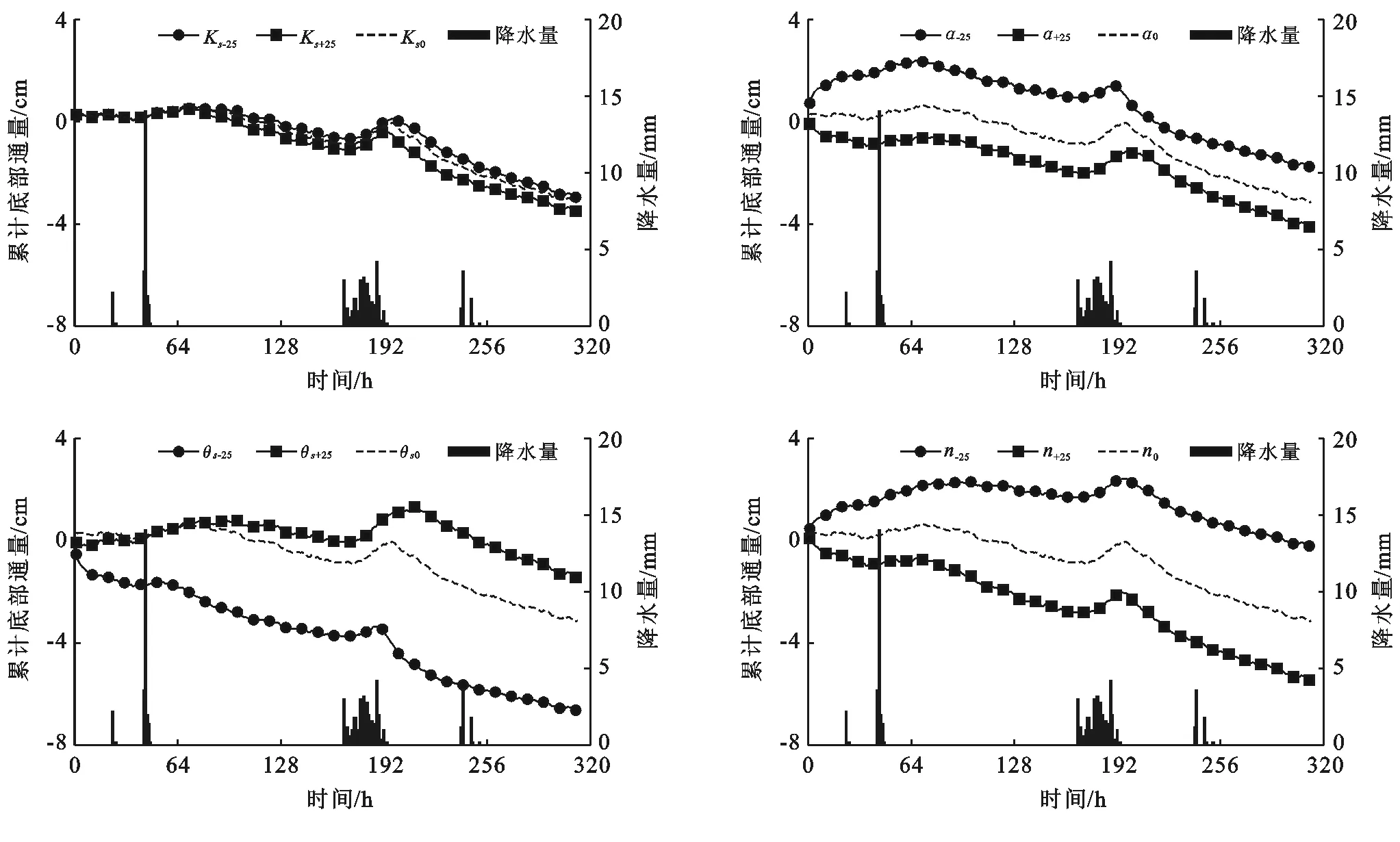
图5 不同参数变化对模拟底部通量的影响

项目α-25n∗-25Ks-25θs-25α+25n∗+25Ks+25θs+25ROV(tend)1.222.930.442.21.783.760.254.44ROV(tmax)9341550241517136018401322630ROV(tmin)1.212.880.310.00751.782.110.00134.42

注：tend表示结束时刻，tmax为ROV(t)最大时刻，tmin为ROV(t)最小时刻； 下标为-25表示在原参数基础上减小25%的参数值，+25表示增加25%的参数值。

3 讨 论

3.1 降水入渗滞后补给的影响因素探讨

由于土地利用变化、气候变化和工农业发展，世界不同地区的土壤水分和地下水正越来越多地受到影响但呈现出不同规律。本文确定的地下水滞后补给时间为4～11 h，小于相近水位埋深下三江平原地区滞后时间(28～50 d)[19]，这是由于后者包气带岩性更细，入渗速率较慢。在大埋深地区，由于入渗补给路径很长，地下水补给滞后时间甚至能达数十至数百年[4，20]。土壤水分分布同样是影响入渗补给的重要因素，按照活塞流入渗理论，包气带含水率响应滞后时间与土壤水分分布的关系可以表示为[21]：

I(t)=(θ0-θi)Zf

(5)

式中：I(t)——累计入渗量；Zf——入渗深度；θ0——入渗面上部含水率；θi——剖面初始含水率。

由公式(5)得知，包气带含水率响应滞后时间随包气带初始含水率增大而减小，而初始含水率反映了前期降水的影响,因此入渗补给除受到本次降水的影响，还受到前期降水的控制。

3.2 多参数敏感性分析

本研究采用的是单参数敏感性计算，能够较为精确得出各个参数的敏感性。但实际的土壤参数之间存在相关性且总是处于一个合理范围。比如θs增大导致降水入渗滞后时间增大，但是θs增大同样会导致Ks增大，后者能促进降水入渗；因此，对于Ks与θs等相关性较强的参数采用多因素分析能更为准确地探讨其敏感性。

3.3 未来研究

由于研究区的地下水埋深浅，降水入渗补给速率相对较快，包气带浅部补给滞后不明显，通过监测数据确定补给滞后时间的精度并不高。此外，研究时段内降水频次高。因此后续研究应当考虑累计降水对于降水入渗的影响并提高浅部包气带监测精度。研究区处在固定沙丘上，地表平缓，侧向径流微弱，故采用一维渗流模型；但场地内稀疏分布着沙柳，干旱时期沙柳吸收水分较强，对土壤水分分布存在影响[22]。同时地下水补给滞后时间小于包气带含水率响应滞后时间，这表明场地中存在不可忽视的优势流通道，可能的原因是场地内包气带岩性不均一或植被根系吸水[23]。因此后续研究也应当针对植被吸水做进一步分析并考虑使用双渗透模型解决优势流问题。

4 结 论

结合原位监测数据，分析了毛乌素沙地地下水浅埋区降水入渗补给规律，利用Hydrus-1D软件建立了降水入渗数值模型，获取了模型水力学参数和热力学参数；分析了van-Genuchten方程主要水力学参数敏感性；为研究包气带和地下水位对降水入渗的响应机制、分析降水入渗补给机理奠定了基础。

(1) 包气带含水率响应深度随着降水量增大而增大，其中小雨型响应深度为3～10 cm，中雨型为30～60 cm，大雨型为60～90 cm，暴雨型均大于90 cm。入渗响应深度与降水量的关系可表示为：D=35.5P-17.1，其中D为入渗响应深度(cm)，P为降水量大小。随着前期累计降水量增大，降水入渗深度也增大。

(2) 研究区内地下水补给滞后时间约为4～11 h。包气带水分和地下水滞后补给受地下水埋深、包气带岩性和含水率分布共同影响，其中包气带水分滞后补给时间随着初始含水率增大而减小。

(3) 建立了该地变饱和带水汽热耦合运移模型。采用模型识别与验证获取了包气带水力学参数与热力学参数，以此作为参数反演优化的初始输入值；参数优化最佳结果θr为0.03，θs为0.34，Ks为23 cm/h,各层n为2.0～2.2，α为0.060～0.074。

(4) 与数值模型有关的各项水力学参数中，敏感性自强到弱的排序是θs，n，α，KS，底部通量对于θs最为敏感；降水补给滞后时长与θs呈正相关关系。